Script per la Scuola di Base
per consolidare apprendimenti, scoprire proprietà, evitare calcoli meccanici e poco significativi, …
(e per esercitarsi senza il controllo dell'insegnante)

A  numeri interi - 1

0 + 100 + 100 + 100 + 10 + 10 + 1 + 1 + 1 + 1 + 1 → 325
0 + 100 + 100 - 1 - 1 - 1→ 197

che numero è?
che numero è?

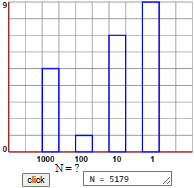
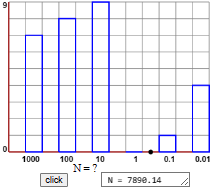
numeri interi - 2

notazione scientifica

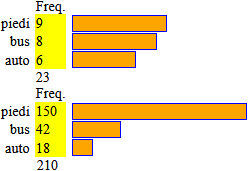
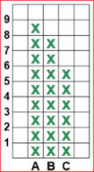B  A 5 anni posso tracciare "a mano" diagrammi a crocette come quello qui a sinistra.  Poi l'insegnante può far interorizzare il legame tra quantità e lunghezze utilizzando istogrammi a quadretti (vedi la figura a destra) che può preparare con questo semplice script (vedi gli esempi). Successivamente l'insegnante può far utilizzare uno script  (diagramma a barre)  per realizzare facilmente diagrammi senza quadretti anche di grandezze maggiori.

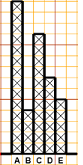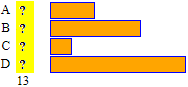
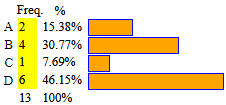
Con questa versione,  diagramma a barre-1,  come raffigurato a destra,  posso tracciare più istogrammi in modo che (vedi sotto) le unioni delle colonne dei vari istogrammi siano ugualmente lunghe.  A livello adulto, questi istogrammi rappresentano le percentuali.                                   Poi, si possono proporre anche degli esercizi astratti, come:                 "trovare A, B, C e D che producano la figura a fianco". In seguito, per avere le percentuali, si può usare  diagramma a barre-2 (figura a destra)  o anche  diagramma a striscia  (figura a sinistra)

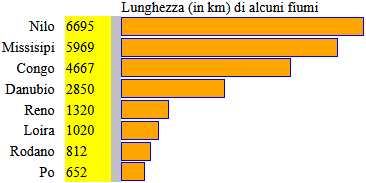Con grafici a barre puoi realizzare semplici grafici

Con grafici a barre di sequenze puoi realizzare istogrammi con la stessa scala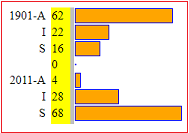

C  numeri decimali

i numeri dell'orologio

metti in ordine numerico

metti in ordine alfabetico

femminile / maschile

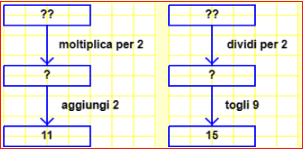
prime equazioni (A)    prime equazioni (B)    prime equazioni (C)    prime equazioni (D)

|||||||||||   QUIZ (esempi)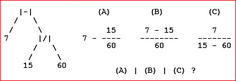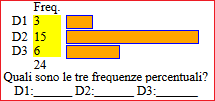

D  prima calcolatrice (chiamiamola CT, Calcolatrice Tascabile)
Primo uso

Posso fare operazioni di somma e sottrazione, ed esplorare operativamente i numeri negativi.
Posso fare moltiplicazioni, costruire le tabelline, esplorare che cosa accade moltiplicando e dividendo per 10, 100, …
Devo osservare che (come in quasi tutto il mondo) si usa "." invece di ",".
Esploro il siginficato del tasto [C].
Scopro che posso introdurre i numeri cifra per cifra con i tasti o posso scriverli direttamente nella casella di input.
Scopro che posso mettere anche una o più di una delle 4 operazioni.
Osservo che posso copiare risultati o scrivere altre cose nelle caselle grige.
Scopro la priorità delle operazioni (1+2*3 → 7, non 9).
Posso imporre un'ordine con cui eseguire le operazioni usando le parentesi: (1+2)*3.

E  divisione (riproduce la divisione a mano)
Scopro che

facendo la divisone tra due numeri interi prima o poi ottengo una cifra che si ripete (0, 1, ..., 9) o un gruppo di cifre, e posso capire che il numero di cifre che si ripetono deve essere inferiore al secondo termine della divisione (nel caso sopra illustrato sono 16).

rapporto  tra due numeri (interi o no) espresso anche in forma percentuale                           (esempi)

pendenza di una retta OP

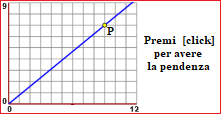
F  calcoli con interi comunque grandi
Somme e prodotti

tra interi sono ovviamente numeri limitati. È facile farne il calcolo, ma è ugualmente facile fare errori di distrazione. Imparato il procedimento su piccoli numeri, ci si può poi approggiare al computer. Ma calcoli con numeri lunghi quasi mai capita di doverli affrontare.

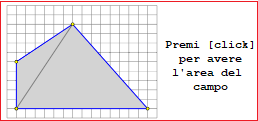
G  area triangolo e parallelogramma
È facile

ricorrendo ad una animazione "dimostrare" quanto vale l'area di un parallelogramma e di un triangolo.

area di semplici quadrilateri

H  prima calcolatrice   2
Secondo uso

Con lo script per calcoli con numeri interi visto poco sopra eseguendo 20/17 ottengo 1.176470588235294117647058823529411…, con questa CT ottengo 1.1764705882, ma posso aumentare il numero delle cifre dopo ".".  Se metto 13 ottengo 1.1764705882353, un arrotondamento alle 13 cifra dopo il "." (...23529... → ...2353 in quanto 9 ≥ 5).  Se metto 1 ottengo 1.2.  Per tutti gli scopri pratici servono poche cifre.
Posso arrotondare anche a cifre prima di ".".  Per trovare quanto devono mettere ciascuna 3 persone per formare 2000 euro faccio 200/3 ottenendo 666.666666667;  se voglio arrotondare agli interi scelgo "0 cifre dopo ." ottenendo 667;  se voglio arrontondare alle decine di euro, scelgo -1 cifre dopo "." (ossia "1 cifra prima di .") ottenendo 670.
Si possono impiegare anche più coppie di parentesi:  ((1+1)*2+1)*2 → 10.
C'è un numero che moltiplicato per sé stesso faccia 10? Se faccio 3*3 ho 9, con 4*4 ho 16; deve stare tra 3 e 4; con 3.1*3.1 ho 9.61, … con 3.16*3.16 ho 9.9856, con 3.17*3.17 ho 10.0489; deve stare tra 3.16 e 3.17; così via posso trovare le altre cifre di un numero che moltiplicato per sé per sé stesso faccia 10:  3.1622776602…  Questo numero si chiama radice quadrata di 10: è il lato in cm di un quadrato che abbia area 10 cm². C'è un modo più semplice per calcolarlo.
Il tasto [rad] consente di calcolare la radice quadrata del numero messo alla sua destra.  Per avere un quadrato di area 130 mm² quanto deve essere lungo il suo lato? Mi basta 1 cifra in più oltre quella dei millimetri.  Scelgo "1" come "cifre dopo ." e clicco [rad] ottenendo 11.4:  posso prendere il lato lungo 11.4 mm (11 millimetri e 4 decimi di millimetro).
Se a destra di [rad] metto un numero positivo qualunque e premo ripetutamente [rad] che cosa ottengo?

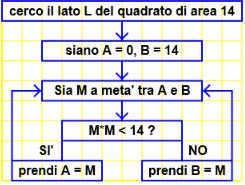
Come viene calcolata la radice quadrata di un numero? Questo script mi consente di capirlo. radice quadrata

I  perimetro e area del cerchio

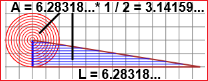
J  prima calcolatrice   3
Terzo uso

Il tasto [PI] premuto dà il numero 3.141592653589793, l'approssimazione a 17 cifre dell'area di un cerchio di raggio 1 (un cerchio di raggio 10 centimetri ha area di 31.4159… cm²).  Questo numero, chiamato pi greca in quanto di solito si scrive π (la "pi" dell'alfabeto greco), è il numero per cui moltiplicare il diametro di un cerchio per ottenere la sua lunghezza.  Se un cerchio ha il diametro di 37.4 cm quanto vale la sua circonferenza?  Calcolo 37.4*3.141592653589793 arrotondando ai decimi (metto "1" come numero di cifre dopo il punto) ottenendo 117.5 (centimetri).
La nostra CT ha anche il tasto [resto]. Che cosa fa?  Se calcolo 200/17 ottengo 11.7647058824;  se arrotondassi agli interi otterrei 12;  il risultato troncato agli interi è 11; per ottenere il resto a mano farei:  17*11 = 187; da 187 a 200 quanto manca? 200-187 = 13.  Il tasto [resto] fa proprio questo calcolo: se batto 200, poi [resto], poi 17 ottengo 13.
In fondo a destra di [Help] vi sono i tasti [R] e [PI] che introducono nella casella in alto il risultato appena calcolato o il valore di π. Ad esenpio per calcolare (123456+654321)*(123456+654321), calcolato 123456+654321 (ottenendo sul visore 777777), basta che aggiunga * e schiacci il tasto [R] per avere 777777*777777. Per ottenere 37.4*3.141592653589793 basta che batta "37.4*" e poi prema il tasto [PI].

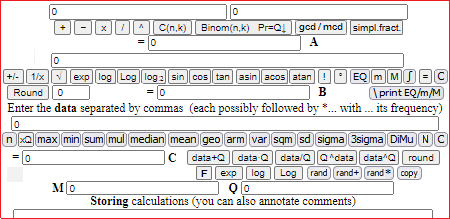Alla fine della scuola di base potrai incominciare ad usare questa calcolatrice più complessa, che svolge anche operazioni il cui significato scoprirai in anni futuri.

K  carta millimetrata Un "foglio" di carta millimetrata per costruire (a mano) grafici di funzioni "sperimentali" (come il peso di una persona al passare degli anni) o espresse da formule.

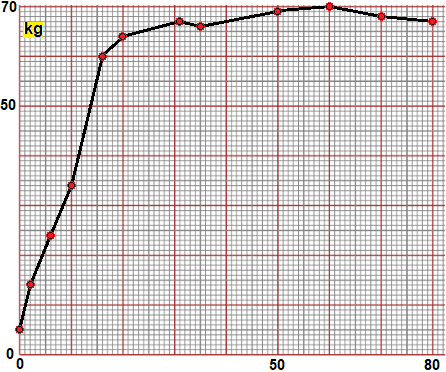
disegnare (1) Come si disegna col computer? Un semplice programmino per avere un'idea di come si fa.

disegno (0)   esempi

disegnare (2)   Disegnare su carta quadrettata col computer disegno (1) (draw) disegno (2) (draw2)

disegnare (3)   (vecchia versione) Disegnare su carta quadrettata col computer (bis)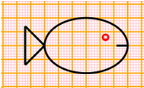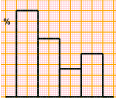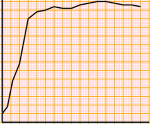

disegnare (4)   (vecchia versione) Disegnare col computer su carta quadrettata / senza quadretti (per l'insegnante)   disegnare (4b)   su carta più ampia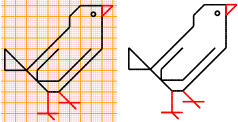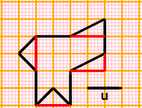

disegnare (5)   (vecchia versione) Disegnare col computer su carta quadrettata / senza quadretti (per l'insegnante) - formato maggiore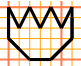

Polimini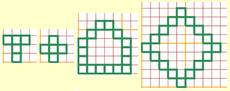

isola tesoro Indicare i passi (nelle direzioni N,S,O,E) per giungere al tesoro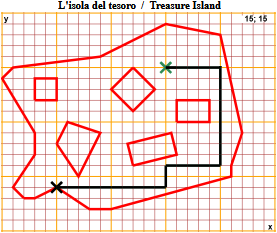

L  percentuali (con la CT farei:  20/160*100 = 12.5)

distribuzioni percentuali

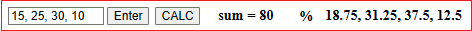
M  cerchio diviso in centesimi                       e semicerchio diviso in cinquantesimi       (per costruire areogrammi)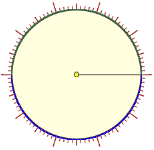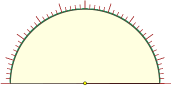

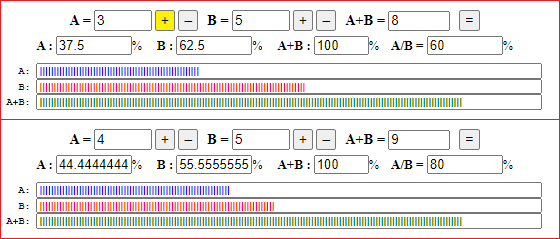
N  somme e rapporti (posso introdurre i numeri direttamente o aumentare o diminuire di 1 il valore di A o di B)

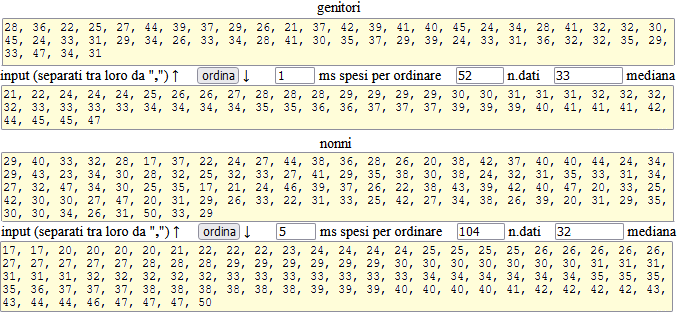
O  ordinamento     (e mediana)
Come ordinare

dei numeri, e, poi, come trovare il dato che separa la prima metà di essi dalla seconda, cioè il dato che sta al centro di essi (o immediatamente prima, se i dati sono in numero pari), ossia la mediana? Un esempio:
Gli alunni di una classe di 4ª elementare raccolgono le età che avevano i genitori quando loro sono nati e le età che avevano i nonni quando sono nati i loro genitori:
genitori: 28, 36, 22, 25, 27, 44, 39, 37, 29, 26, 21, 37, 42, 39, 41, 40, 45, 24, 34, 28, 41, 32, 32, 30, 45, 24, 33, 31, 29, 34, 26, 33, 34, 28, 41, 30, 35, 37, 29, 39, 24, 33, 31, 36, 32, 32, 35, 29, 33, 47, 34, 31
nonni: 29, 40, 33, 32, 28, 17, 37, 22, 24, 27, 44, 38, 36, 28, 26, 20, 38, 42, 37, 40, 40, 44, 24, 34, 29, 43, 23, 34, 30, 28, 32, 25, 32, 33, 27, 41, 29, 35, 38, 30, 38, 24, 32, 31, 35, 33, 31, 34, 27, 32, 47, 34, 30, 25, 35, 17, 21, 24, 46, 39, 37, 26, 22, 38, 43, 39, 42, 40, 47, 20, 33, 25, 42, 30, 30, 27, 47, 20, 31, 29, 26, 33, 22, 31, 33, 25, 42, 27, 34, 38, 26, 39, 20, 31, 29, 35, 30, 30, 34, 26, 31, 50, 33, 29
Si vede (con lo script) che l'età mediana è sempre di poco superiore ai 30 anni (anche se il numero di figli per coppia di nonni un tempo era maggiore).  L'ordinamento si potrebbe fare a mano: si capisce che è una cosa facile (trovo il dato più piccolo, lo tolgo dalla lista, trovo il nuovo dato più piccolo, lo tolgo dalla lista, …) e è facile, poi, trovare il dato "mediano", ma se i dati sono molti la cosa richiede parecchio tempo: meglio usare il computer.  In questo modo posso, ad esempio, valutare facilmente come nel tempo è cambiata la altezza dei ragazzi di una classe di scuola, senza confrontare le altezze dei singoli.  La mediana è un concetto semplice ma è uno dei concetti matematici più utili.

Naturalmente, come gli altri script, questo è utile per pro- porre agli alunni delle attività in cui possono esercitarsi da soli, e controllare le risposte senza l'intervento del docente!

Oltre alla mediana (32) compaiono anche il dato che delimita il primo quarto di dati (27) e il dato che delimita il primo 3 quarti di dati (38), e la loro differenza (11), cioè l'ampiezza dell'intervallo in cui sta la metà centrale dei dati.

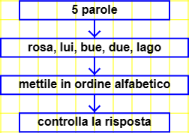
  ordinamento di parole
  scritte in caratteri minuscoli, separate da virgole.

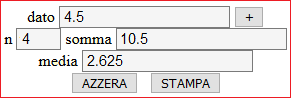
P  media
La media è un "valore medio" diverso dalla mediana. Un paio di esempi. La media delle altezze di due persone è il valore che sta a metà tra esse. Il consumo medio di latte dei membri di una famiglia è la somma dei consumi individuali divisa per il numero dei membri. Vedrai negli anni futuri l'utilità del confronto tra media e mediana.

Q  frazioni     semplificazioni
Il calcolo frazionario

non è certamente uno degli aspetti più significativi delle attività matematica (lo era parecchi anni fa, quando non erano diffusi i mezzi di calcolo ed era importante operare a mano con le frazioni).  È comunque importante operare con i rapporti, fare, quando serve, qualche semplificazione, …  Questi script ti consentono di allenarti a svolgere qualche semplice calcolo: prova a farlo a mano e confronta il risultato col computer.  Il primo fa il calcolo tra frazioni.  Il secondo semplifica una frazione trovando il massimo numero intero per cui sono divisibili i due termini (24 e 100 sono entrambi divisibili per 4). Naturalmente non sempre è utile semplificare una frazione; anche nel caso dell'esempio, 24/100 è certamente più espressivo di 6/25.
Di fronte a un calcolo "complesso" come il seguente  (che devo cercare di fare a mano:  3/4 = 0.75,  3/4+0.25 = 1,  7.5=15/2,  15/2-5/2 = 10/2 = 5, …)  posso controllare il risultato  (di tutto o di qulche parte)  usando la calcolatrice vista sopra.  Se vi introduco  (3/4+7.5+0.25-5/2)*(3/2+7/10-1/2+4.3)  ottengo 36.

3 5 3 7 1 ( — + 7.5 + 0.25 - — )·( — + —— - — + 4.3 ) 4 2 2 10 2

R  divisori

Per consolidare la padronanza dei numeri (e dei rapporti tra numeri) è utile anche riflettere ed esercitarsi su quali sono i divisori e  ...

S  scomposizione in         fattori primi

  ...  su quali di questi sono numeri primi.

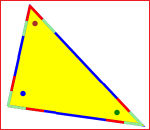
T  somma degli angoli di un triangolo
È facile dedurre che la somma degli angoli di un triangolo è un angolo piatto: muovendosi lungo i lati ritorno nella posizione iniziale facendo mezzo giro, ossia ruotando di 180°.
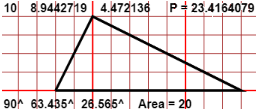
angoli / lati / area di un triangolo
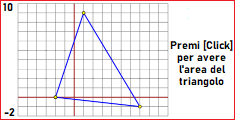
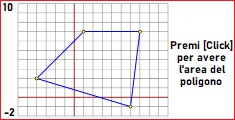
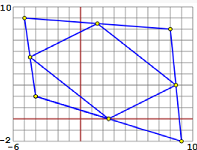
È possibie esplorare i legami tra le misure dei lati e degli angoli di un triangolo, esplorare il loro legame con l'area di esso, e congetturare il teorema sotto dimostrato.

Calcoli di aree e congetture:   area triangolo  -  area quadrangolo  -  un teorema  (vedi)

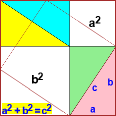
U  Teorema di Piatgora           Le figure precedenti richiamano casi in cui bastano 3 tra angoli e lati per conoscere le altre dimensioni di un triangolo. Un caso particolare è quello in cui un angolo è retto:  posso facilmente dati due lati trovare il terzo.

V  le misure sono approssimate
Come abbiamo richiamato nel punto H, nella pratica non sono molte le cifre con cui possiamo conoscere una grandezza, specie se la "misuriamo".

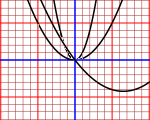
W  parabole (e rette)
Le formule oltre che per fare calcoli servono anche per descrivere figure, come le rette e le parabole. Con questo script posso tracciare facilmente sia rette che parabole, dopo aver imparato a tracciarle a mano (per le rette riduci "a" fino a farlo valere 0).
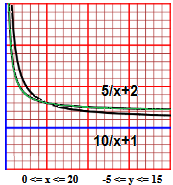
iperboli  (funzioni con grafico iperbolico,             anche senza chiamarlo così)
La nostra classe va a visitare un museo. Il prezzo per le scuole è di 10 € più 1 € per ogni alunno.  Qual è il grafico della spesa individuale al variare del numero dei partecipanti, da 1 a 20? Se il prezzo fosse di 5 € più 2 € per alunno, fino a che numero di alunni converebbe questa seconda tariffa?

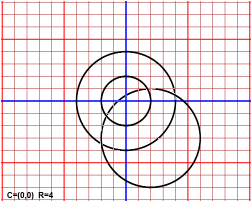
X  cerchi
In un analogo piano dotato di coordinate posso tracciare cerchi. Posso modificare la posizione del centro e cambiare il raggio.
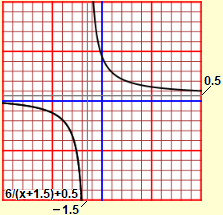
iperboli  (anche per x negativi)

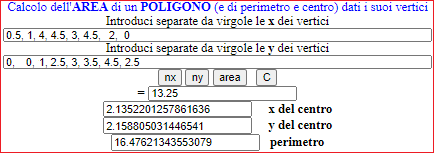
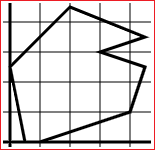
Y  area triangoli,  poligoni      area, perimetro, centro
Perimetro ed area di un poligono

sappiamo calcolarle trovando le misure dei lati col teorema di Pitagora e l'area suddividendo il poligono in triangoli.  Questo script automatizza il procedimento.  Lo script trova anche il "centro" del poligono; il significato e il calcolo del "centro" lo sai trovare solo nel caso dei rettangoli e di altri poligoni particolari; come procedere in generale lo vedrai nei livelli scolastici successivi.

Z  istogrammi (a partire da dati singoli)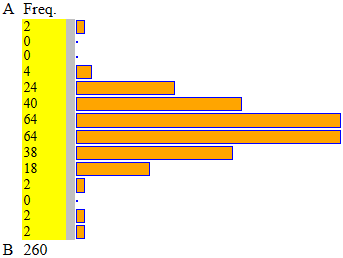

Abbiamo visto in B come tracciare semplici istogrammi. Supponiamo di disporre di una sequenza di dati non classificati, come le seguenti misure (in cm) delle lunghezze di una certa quantità di fave, misurate da degli alunni di 12 anni. Con questo script possiamo scegliere un intervallo in cui stanno di dati e dividerlo in tanti intervallini, in modo da rappresentare come i dati si distribuiscono in questi intervalli. A destra ciò che possiamo ottenere.

A = 1     B = 2.4     intervalli = 14   di ampiezza 0.1   min=1  max=2.3  -   fave
1.35, 1.65, 1.80, 1.40, 1.65, 1.80, 1.40, 1.65, 1.85, 1.40, 1.65, 1.85, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 2.25, 1.55, 1.70, 1.55, 1.70, 1.55, 1.70, 1.60, 1.70, 1.60, 1.75, 1.60, 1.75, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.00, 1.55, 1.70, 1.75, 1.30, 1.55, 1.70, 1.75, 1.40, 1.60, 1.70, 1.75, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.45, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.75, 1.90, 1.50, 1.60, 1.75, 1.90, 1.50, 1.65, 1.75, 1.90, 1.55, 1.65, 1.75, 1.95, 1.55, 1.65, 1.75, 2.00, 1.55, 1.65, 1.75, 2.30, 1.35, 1.65, 1.80, 1.40, 1.65, 1.80, 1.40, 1.65, 1.85, 1.40, 1.65, 1.85, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 2.25, 1.55, 1.70, 1.55, 1.70, 1.55, 1.70, 1.60, 1.70, 1.60, 1.75, 1.60, 1.75, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.00, 1.55, 1.70, 1.75, 1.30, 1.55, 1.70, 1.75, 1.40, 1.60, 1.70, 1.75, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.45, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.75, 1.90, 1.50, 1.60, 1.75, 1.90, 1.50, 1.65, 1.75, 1.90, 1.55, 1.65, 1.75, 1.95, 1.55, 1.65, 1.75, 2.00, 1.55, 1.65, 1.75, 2.30

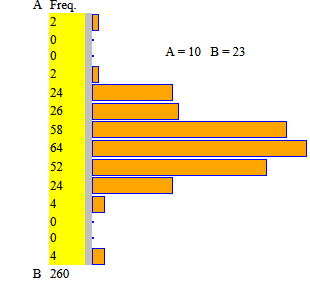
Nel caso i dati siano interi, come i dati precedenti espressi in millimetri, si può ricorrere ad uno script molto più semplice,  istogrammi a partire da dati interi,  in cui basta inserire i dati senza introdurre altri input: 14, 17, 18, 14, 17, 18, 14, 17, 19, 14, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 23, 16, 17, 16, 17, 16, 17, 16, 17, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 10, 16, 17, 18, 13, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 19, 15, 16, 17, 19, 15, 16, 18, 19, 15, 16, 18, 19, 15, 17, 18, 19, 16, 17, 18, 20, 16, 17, 18, 20, 16, 17, 18, 23, 14, 17, 18, 14, 17, 18, 14, 17, 19, 14, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 23, 16, 17, 16, 17, 16, 17, 16, 17, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 10, 16, 17, 18, 13, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 19, 15, 16, 17, 19, 15, 16, 18, 19, 15, 16, 18, 19, 15, 17, 18, 19, 16, 17, 18, 20, 16, 17, 18, 20, 16, 17, 18, 23

altro software         ALTRO