
Basic School Scripts
to consolidate learning, discover properties, avoid mechanical and insignificant calculations, …
(and to practice without teacher control)
| A integers - 1 |

|
what number is it?
what number is it?
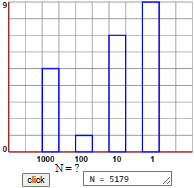
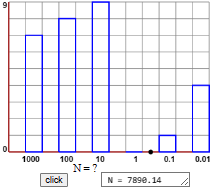
| integers - 2 |  |
| scientific notation |

|
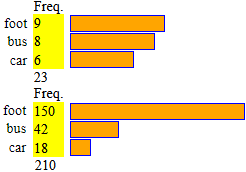
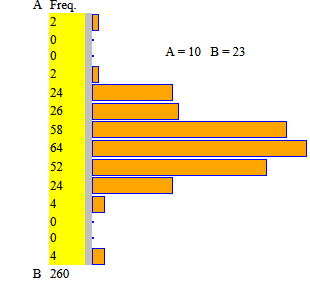
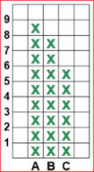 | B At the age of 5, I can draw "by hand" cross diagrams like the one on the left. Then the teacher can make the pupils internalize the link between quantities and lengths using histograms with squares (see the figure on the right) which he can prepare with this simple script (see the examples).
| 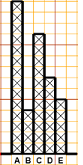 |
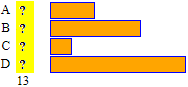
With this version, block diagrams-1, as depicted on the right, I can draw multiple histograms so that (see below) the joins of the columns of the various histograms are equally long. At the adult level, these histograms represent percentages. Then, abstract exercises can also be proposed, such as: "find A, B, C and D that produce the figure alongside". Then, to get the percentages, I can use block diagrams-2 (right figure) or also strip diagrams (left figure) |
|
 | 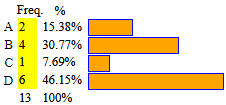 |
 | With bar graphs you can make simple charts |
| By bar graphs of sequences you can make histograms with the same scale | 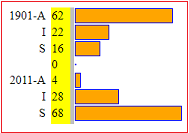 |
| C decimal numbers |

|
| the numbers of the clock | 
|
first equations (A) first equations (B) first equations (C) first equations (D)
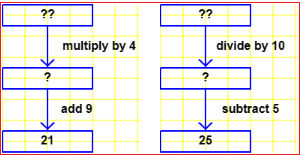
| ||||||||||| QUIZ (examples) | 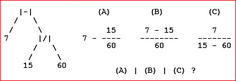 | 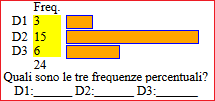 |
 |
| D pocket calculator |
|
| First use |
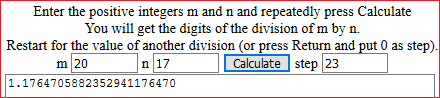
| E division (it reproduces the division by hand) |
|
| I discover that |
ratio between two (whole or not) numbers, also in percentage form (examples) |

|
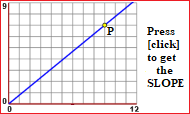
| slope of a line OP |
|
| F calculations with anyway large integers |

|
| Sums and products |
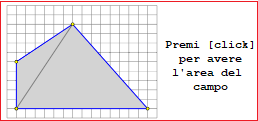
| G area triangle and parallelogram |

|
| It is easy |
| H pocket calculator 2 |

|
| Second use |
How is the square root of a number calculated? |
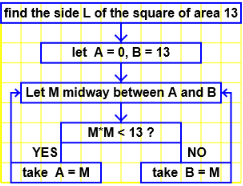 |
| I perimeter and area of the circle |
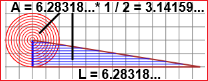
|
| J pocket calculator 3 |

|
| Third use |
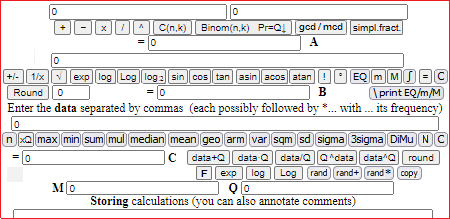 | At the end of basic school you will be able to start using this more complex calculator, which also performs operations whose meaning you will discover in future years. |
| K
graph paper A "sheet" of graph paper to build (by hand) graphs of "experimental" functions (such as the weight of a person over the years) or functions expressed by formulas. |
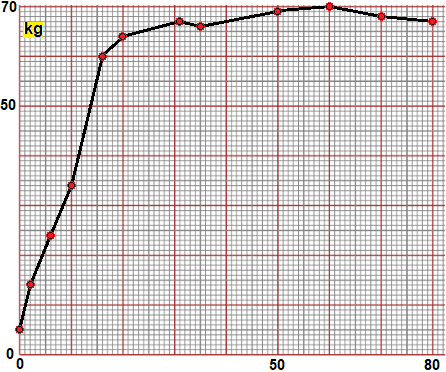
|
|
drawing (1) How is a drawing done with a computer? A simple program to get an idea of how it's done. |
|
|
draw (0) examples |  |
|
drawing (2) How to draw on squared paper draw (1) (draw) draw (2) (draw2) |
|
|
drawing (3) (old version) How to draw on squared paper using the computer (bis) |     |
|
drawing (4) (old version) How to draw (using the computer) on squared paper /paper without squares (for the teacher) drawing (4b) on larger paper | 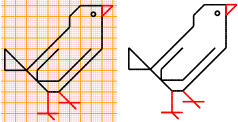 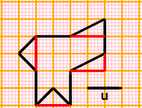 |
|
drawing (5) (old version) How to draw (using the computer) on squared paper /paper without squares (for the teacher) - larger size |  |
| Polyomino | 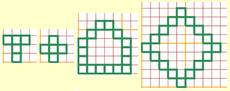 |
| Treasure Island Indicate the steps (in the N,S,W,E directions) to reach the treasure. | 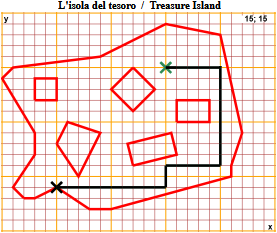 |
| L
percentages (with our calculator I would do: 20/160*100 = 12.5) |  |
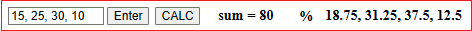
| M
circle divided into cents and semicircle divided into fiftieths (to construct areograms) | 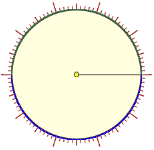 | 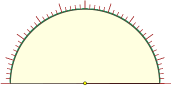 |
| N
sums and ratios (I can enter the numbers directly or increase or decrease the value of A or B by 1) |
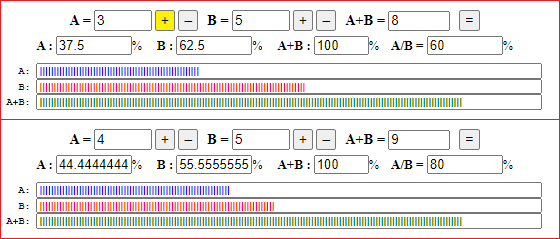
|
| O
sorting (and median) |
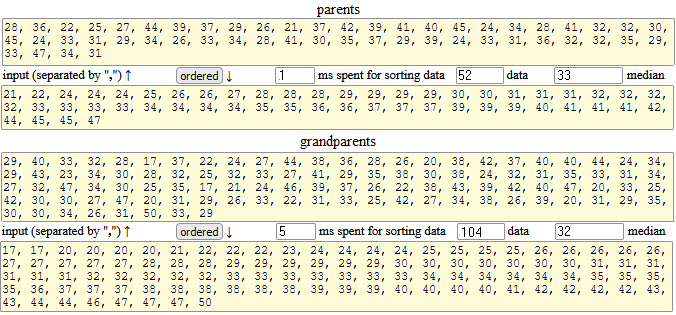
|
| How to order |
 |
Of course, like the other scripts, this is useful for proposing to the pupils activities they can practice on their own, and check the answers without the intervention of the teacher! |
| In addition to the median (32), there are also the datum that delimits the first quarter of data (27) and the datum that delimits the first 3 quarters of data (38), and their difference (11), i.e. the width of the interval where the middle half of the data is. |
  |
ordering of words
written in lowercase characters, separated by commas.

| P mean |
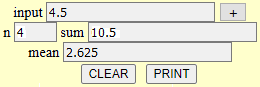 
|
|
The mean is an "average value" other than the median. A couple of examples. The average of the heights of two people is the value that is halfway between them. The average milk consumption of family members is the sum of individual consumption divided by the number of members. You will see in future years the usefulness of the comparison between mean and median. |
| Q
fractions simplifying fractions |
 
|
| Fractional calculus |
|
| R divisors |

|
| S prime factorization |

|
| T sum angles of triangle |
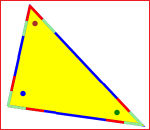
|
|
It is easy to deduce that the sum of the angles of a triangle is a flat angle: moving along the sides, I return to the initial position by making half a turn, that is, rotating by 180° | |
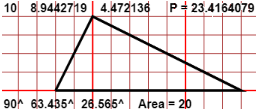
| angles / sides / area of a triangle |
|
|
It is possible to explore the links between the measurements of the sides and angles of a triangle, explore their link with the area of it, and conjecture the theorem proved below. |
Calculations of areas and conjectures: area triangles - area quadrangles - a theorem (see)
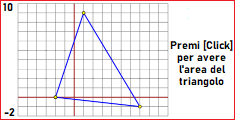 | 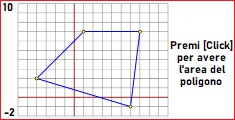 | 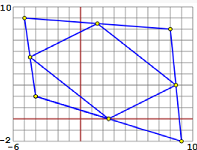 |
U
Pythagoras Theorem The previous figures recall cases in which 3 angles or sides are enough to know the other dimensions of a triangle. A special case is that in which an angle is right: given two sides I can easily find the third. |
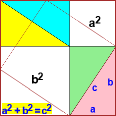
|
| V the measurements are approximate |

|
|
As we recalled in point H, in practice there are not many figures with which we can know a quantity, especially if we "measure it". |
| W parables (and lines) |
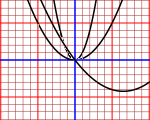
|
|
In addition to making calculations, formulas are also used to describe figures, such as lines and parables. With this script I can easily draw both lines and parabolas, after having learned to draw them by hand (for the lines reduce "a" until it is equal to 0). | |
hyperbolas (functions with hyperbolic graph, even without calling it that) |
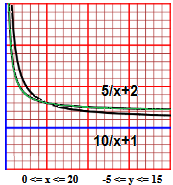
|
Our class goes to visit a museum. The price for schools is €10 plus €1 for each pupil. What is the graph of individual spending as the number of participants varies, from 1 to 20? If the price were €5 plus €2 per pupil, up to what number of pupils would this second rate be worth it? |
| X circles |
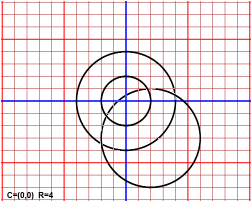 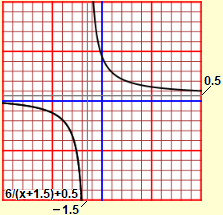
|
In a similar plane, with coordinates, I can draw circles. I can change the position of the center and change the radius. |
| hyperbolas (even for negative x) |
| Y
area triangles, polygons area, perimeter, center |
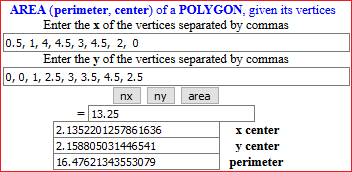 
|
| Perimeter and area of a polygon: |
| Z histograms (starting from single data) | 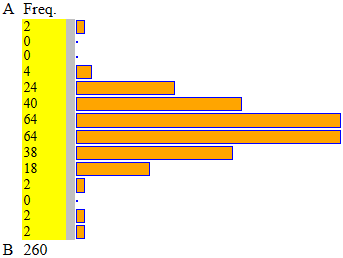
|
|
We have seen in B how to draw simple histograms. Suppose we have a sequence of unclassified data, such as the following measurements (in cm) of the lengths of a certain number of beans, measured by 12-year-old pupils. With this script we can choose an interval in which there are data and divide it into many intervals, in order to represent how the data is distributed in these intervals. Right what we can get. |
| If the data are integers, like the previous data expressed in millimetres, a much simpler script can be used,
histograms starting from integer data, in which it is enough to enter the data without introducing other inputs: 14, 17, 18, 14, 17, 18, 14, 17, 19, 14, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 23, 16, 17, 16, 17, 16, 17, 16, 17, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 10, 16, 17, 18, 13, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 19, 15, 16, 17, 19, 15, 16, 18, 19, 15, 16, 18, 19, 15, 17, 18, 19, 16, 17, 18, 20, 16, 17, 18, 20, 16, 17, 18, 23, 14, 17, 18, 14, 17, 18, 14, 17, 19, 14, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 19, 15, 17, 23, 16, 17, 16, 17, 16, 17, 16, 17, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 16, 18, 10, 16, 17, 18, 13, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 14, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 18, 15, 16, 17, 19, 15, 16, 17, 19, 15, 16, 18, 19, 15, 16, 18, 19, 15, 17, 18, 19, 16, 17, 18, 20, 16, 17, 18, 20, 16, 17, 18, 23 |
 |