source("http://macosa.dima.unige.it/r.R") # If I have not already loaded the library
---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
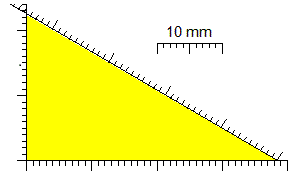 # catheti: 22 ≤ a ≤ 23, 38 ≤ b ≤ 39 → hypotenuse: 43.9 ≤ c ≤ 45.3
a = c(22, 23); b = c(38, 39)
a2 = approx(a,2,"^"); a2; b2 = approx(b,2,"^"); b2
# min max
# 484 529
# min max
# 1444 1521
c2 = approx(a2,b2, "+"); c2; c = approx(c2,1/2,"^"); c
# min max
# 1928 2050
# min max
# 43.90900 45.27693
# or:
approx( approx( approx(a,2,"^"), approx(b,2,"^"), "+"), 1/2, "^")
# 43.90900 45.27693
# Here's how to build the figure (with a=22.5, b=38.5):
BF=3.2; HF=3*26/40.5
BOXW(-1/2,40,-1,25)
a = 38.5; b = 22.5
polyC(c(0,a,0),c(0,0,b),"yellow")
polyl(c(0,a,0),c(0,0,b),"white")
line(0,0, 40,0, 1)
line(0,0, 0,25, 1)
halfl(a,0, 0,b, 1)
for(i in 0:40) line(i,-0.7,i,0, 1)
for(i in 0:4) line(i*10,-1.5,i*10,0, 1)
for(i in 0:25) line(-0.7,i,0,i, 1)
for(i in 0:3) line(-1.5,i*10,0,i*10, 1)
ang2 = 90-atan(b/a)/pi*180; ang1=90+ang2
for(i in 0:50) { X=a+xrot(ang1)*i; Y=yrot(ang1)*i
X1=a+xrot(ang1)*i+xrot(ang2)*0.7; Y1=yrot(ang1)*i+yrot(ang2)*0.7
line(X,Y, X1,Y1, 1) }
for(i in 0:5) { X=a+xrot(ang1)*10*i+xrot(ang2)*0.7; Y=yrot(ang1)*10*i+yrot(ang2)*0.7
X1=a+xrot(ang1)*10*i+xrot(ang2)*1.5; Y1=yrot(ang1)*10*i+yrot(ang2)*1.5
line(X,Y, X1,Y1, 1) }
for(i in 0:10) line(i+20,-0.7+18,i+20,0+18, 1)
for(i in c(0,1/2,1)) line(i*10+20,-1.5+18,i*10+20,0+18, 1)
line(20,18, 30,18, 1)
text(25,20,"10 mm",cex=0.9)
# With the same commands (with a=22,b=38; a=23, b=39) I get:
# catheti: 22 ≤ a ≤ 23, 38 ≤ b ≤ 39 → hypotenuse: 43.9 ≤ c ≤ 45.3
a = c(22, 23); b = c(38, 39)
a2 = approx(a,2,"^"); a2; b2 = approx(b,2,"^"); b2
# min max
# 484 529
# min max
# 1444 1521
c2 = approx(a2,b2, "+"); c2; c = approx(c2,1/2,"^"); c
# min max
# 1928 2050
# min max
# 43.90900 45.27693
# or:
approx( approx( approx(a,2,"^"), approx(b,2,"^"), "+"), 1/2, "^")
# 43.90900 45.27693
# Here's how to build the figure (with a=22.5, b=38.5):
BF=3.2; HF=3*26/40.5
BOXW(-1/2,40,-1,25)
a = 38.5; b = 22.5
polyC(c(0,a,0),c(0,0,b),"yellow")
polyl(c(0,a,0),c(0,0,b),"white")
line(0,0, 40,0, 1)
line(0,0, 0,25, 1)
halfl(a,0, 0,b, 1)
for(i in 0:40) line(i,-0.7,i,0, 1)
for(i in 0:4) line(i*10,-1.5,i*10,0, 1)
for(i in 0:25) line(-0.7,i,0,i, 1)
for(i in 0:3) line(-1.5,i*10,0,i*10, 1)
ang2 = 90-atan(b/a)/pi*180; ang1=90+ang2
for(i in 0:50) { X=a+xrot(ang1)*i; Y=yrot(ang1)*i
X1=a+xrot(ang1)*i+xrot(ang2)*0.7; Y1=yrot(ang1)*i+yrot(ang2)*0.7
line(X,Y, X1,Y1, 1) }
for(i in 0:5) { X=a+xrot(ang1)*10*i+xrot(ang2)*0.7; Y=yrot(ang1)*10*i+yrot(ang2)*0.7
X1=a+xrot(ang1)*10*i+xrot(ang2)*1.5; Y1=yrot(ang1)*10*i+yrot(ang2)*1.5
line(X,Y, X1,Y1, 1) }
for(i in 0:10) line(i+20,-0.7+18,i+20,0+18, 1)
for(i in c(0,1/2,1)) line(i*10+20,-1.5+18,i*10+20,0+18, 1)
line(20,18, 30,18, 1)
text(25,20,"10 mm",cex=0.9)
# With the same commands (with a=22,b=38; a=23, b=39) I get:
 - - - - - - - - - - - - - - - - - -
# If I want to verify if it is possible that the initial triangle is right:
- - - - - - - - - - - - - - - - - -
# If I want to verify if it is possible that the initial triangle is right:
 # 22 ≤ a ≤ 23, 38 ≤ b ≤ 39, 44 ≤ c ≤ 45
# I must verify that the square root of the sum of the squares of the cathets,
# [43.90900, 45.27693], has a non-empty intersection with the interval that represents
# the hypotenuse c measured directly, [44, 45]: OK
# The intersection is: [43.9, 45]
Back
# 22 ≤ a ≤ 23, 38 ≤ b ≤ 39, 44 ≤ c ≤ 45
# I must verify that the square root of the sum of the squares of the cathets,
# [43.90900, 45.27693], has a non-empty intersection with the interval that represents
# the hypotenuse c measured directly, [44, 45]: OK
# The intersection is: [43.9, 45]
Back
 # catheti: 22 ≤ a ≤ 23, 38 ≤ b ≤ 39 → hypotenuse: 43.9 ≤ c ≤ 45.3
a = c(22, 23); b = c(38, 39)
a2 = approx(a,2,"^"); a2; b2 = approx(b,2,"^"); b2
# min max
# 484 529
# min max
# 1444 1521
c2 = approx(a2,b2, "+"); c2; c = approx(c2,1/2,"^"); c
# min max
# 1928 2050
# min max
# 43.90900 45.27693
# or:
approx( approx( approx(a,2,"^"), approx(b,2,"^"), "+"), 1/2, "^")
# 43.90900 45.27693
# Here's how to build the figure (with a=22.5, b=38.5):
BF=3.2; HF=3*26/40.5
BOXW(-1/2,40,-1,25)
a = 38.5; b = 22.5
polyC(c(0,a,0),c(0,0,b),"yellow")
polyl(c(0,a,0),c(0,0,b),"white")
line(0,0, 40,0, 1)
line(0,0, 0,25, 1)
halfl(a,0, 0,b, 1)
for(i in 0:40) line(i,-0.7,i,0, 1)
for(i in 0:4) line(i*10,-1.5,i*10,0, 1)
for(i in 0:25) line(-0.7,i,0,i, 1)
for(i in 0:3) line(-1.5,i*10,0,i*10, 1)
ang2 = 90-atan(b/a)/pi*180; ang1=90+ang2
for(i in 0:50) { X=a+xrot(ang1)*i; Y=yrot(ang1)*i
X1=a+xrot(ang1)*i+xrot(ang2)*0.7; Y1=yrot(ang1)*i+yrot(ang2)*0.7
line(X,Y, X1,Y1, 1) }
for(i in 0:5) { X=a+xrot(ang1)*10*i+xrot(ang2)*0.7; Y=yrot(ang1)*10*i+yrot(ang2)*0.7
X1=a+xrot(ang1)*10*i+xrot(ang2)*1.5; Y1=yrot(ang1)*10*i+yrot(ang2)*1.5
line(X,Y, X1,Y1, 1) }
for(i in 0:10) line(i+20,-0.7+18,i+20,0+18, 1)
for(i in c(0,1/2,1)) line(i*10+20,-1.5+18,i*10+20,0+18, 1)
line(20,18, 30,18, 1)
text(25,20,"10 mm",cex=0.9)
# With the same commands (with a=22,b=38; a=23, b=39) I get:
# catheti: 22 ≤ a ≤ 23, 38 ≤ b ≤ 39 → hypotenuse: 43.9 ≤ c ≤ 45.3
a = c(22, 23); b = c(38, 39)
a2 = approx(a,2,"^"); a2; b2 = approx(b,2,"^"); b2
# min max
# 484 529
# min max
# 1444 1521
c2 = approx(a2,b2, "+"); c2; c = approx(c2,1/2,"^"); c
# min max
# 1928 2050
# min max
# 43.90900 45.27693
# or:
approx( approx( approx(a,2,"^"), approx(b,2,"^"), "+"), 1/2, "^")
# 43.90900 45.27693
# Here's how to build the figure (with a=22.5, b=38.5):
BF=3.2; HF=3*26/40.5
BOXW(-1/2,40,-1,25)
a = 38.5; b = 22.5
polyC(c(0,a,0),c(0,0,b),"yellow")
polyl(c(0,a,0),c(0,0,b),"white")
line(0,0, 40,0, 1)
line(0,0, 0,25, 1)
halfl(a,0, 0,b, 1)
for(i in 0:40) line(i,-0.7,i,0, 1)
for(i in 0:4) line(i*10,-1.5,i*10,0, 1)
for(i in 0:25) line(-0.7,i,0,i, 1)
for(i in 0:3) line(-1.5,i*10,0,i*10, 1)
ang2 = 90-atan(b/a)/pi*180; ang1=90+ang2
for(i in 0:50) { X=a+xrot(ang1)*i; Y=yrot(ang1)*i
X1=a+xrot(ang1)*i+xrot(ang2)*0.7; Y1=yrot(ang1)*i+yrot(ang2)*0.7
line(X,Y, X1,Y1, 1) }
for(i in 0:5) { X=a+xrot(ang1)*10*i+xrot(ang2)*0.7; Y=yrot(ang1)*10*i+yrot(ang2)*0.7
X1=a+xrot(ang1)*10*i+xrot(ang2)*1.5; Y1=yrot(ang1)*10*i+yrot(ang2)*1.5
line(X,Y, X1,Y1, 1) }
for(i in 0:10) line(i+20,-0.7+18,i+20,0+18, 1)
for(i in c(0,1/2,1)) line(i*10+20,-1.5+18,i*10+20,0+18, 1)
line(20,18, 30,18, 1)
text(25,20,"10 mm",cex=0.9)
# With the same commands (with a=22,b=38; a=23, b=39) I get:
 - - - - - - - - - - - - - - - - - -
# If I want to verify if it is possible that the initial triangle is right:
- - - - - - - - - - - - - - - - - -
# If I want to verify if it is possible that the initial triangle is right:
 # 22 ≤ a ≤ 23, 38 ≤ b ≤ 39, 44 ≤ c ≤ 45
# I must verify that the square root of the sum of the squares of the cathets,
# [43.90900, 45.27693], has a non-empty intersection with the interval that represents
# the hypotenuse c measured directly, [44, 45]: OK
# The intersection is: [43.9, 45]
Back
# 22 ≤ a ≤ 23, 38 ≤ b ≤ 39, 44 ≤ c ≤ 45
# I must verify that the square root of the sum of the squares of the cathets,
# [43.90900, 45.27693], has a non-empty intersection with the interval that represents
# the hypotenuse c measured directly, [44, 45]: OK
# The intersection is: [43.9, 45]
Back