# Calcoliamo l'area dello spicchio raffigurato sotto a sinistra
BF=3; HF=3
PIANO(0,5,0,5)
f=function(x) sqrt(25-x^2); g=function(x) 3/4*x
graf(f,-5,5,"blue"); graf(g,-5,5,"blue")
grafico(f,4,5,"red"); grafico(g,0,4,"red"); segm(0,0, 5,0, "red")
# Questa è la figura. È uno spicchio di cerchio. Posso prendere l'area del
# cerchio moltiplicata per il rapporto tra l'angolo dello spicchio e 360°:
A=c(5,0); B=c(0,0); C=c(4,3); angolo(A,B,C)
# 36.8699
pi*5^2*angolo(A,B,C)/360
# 8.043764 Questa è l'area cercata
#
# In alternativa faccio l'area del triangolo e della parte rimanente in cui
# la figura è spezzata dal segmento vericale che scende da (4,3):
spezza(c(4,4),c(0,3),"blue")
# l'area del triangolo più l'integrale di f tra 4 e 5:
4*3/2 + integrale(f,4,5)
# 8.043764
 # Calcoliamo l'area della figura sopra al centro:
PIANO(0,1, 0,1)
f=function(x) x^2; g=function(x) x
grafico(f,0,1, "blue"); grafico(g,0,1,"red")
# La differenza tra l'area sotto al grafico di g e quella sotto a quello di f:
integrale(g,0,1)-integrale(f,0,1)
# 0.1666667
# Ovvero:
h = function(x) g(x)-h(x); integrale(h,0,1)
# 0.1666667 che equivale a:
frazio(integrale(h,0,1))
# 1/6 Questa è l'area cercata
#
# L'area della figura sopra a destra, tra le due curve
PIANO(0,4,-2,2)
f = function(x) sin(x); g = function(x) (x-2)^2
grafico(f,0,4, "red"); grafico(g,0,4, "blue")
soluz2(f,g,1,2)
# 1.064761
soluz2(f,g,2,3)
# 2.67242
h = function(x) f(x)-g(x)
integrale(h, soluz2(f,g,1,2), soluz2(f,g,2,3))
# 1.002636 Questa è l'area cercata
# poco più di un "quadretto"
#
# How to calculate areas enclosed by polar curves.
# Calcoliamo l'area della figura sopra al centro:
PIANO(0,1, 0,1)
f=function(x) x^2; g=function(x) x
grafico(f,0,1, "blue"); grafico(g,0,1,"red")
# La differenza tra l'area sotto al grafico di g e quella sotto a quello di f:
integrale(g,0,1)-integrale(f,0,1)
# 0.1666667
# Ovvero:
h = function(x) g(x)-h(x); integrale(h,0,1)
# 0.1666667 che equivale a:
frazio(integrale(h,0,1))
# 1/6 Questa è l'area cercata
#
# L'area della figura sopra a destra, tra le due curve
PIANO(0,4,-2,2)
f = function(x) sin(x); g = function(x) (x-2)^2
grafico(f,0,4, "red"); grafico(g,0,4, "blue")
soluz2(f,g,1,2)
# 1.064761
soluz2(f,g,2,3)
# 2.67242
h = function(x) f(x)-g(x)
integrale(h, soluz2(f,g,1,2), soluz2(f,g,2,3))
# 1.002636 Questa è l'area cercata
# poco più di un "quadretto"
#
# How to calculate areas enclosed by polar curves.

 # In the case of a circle of radius R I have that area A is pi*R^2.
# Generalizing, if R=R(t):
# In the case of a circle of radius R I have that area A is pi*R^2.
# Generalizing, if R=R(t):
 # If the angle t changes from H to K:
# RR = function(t) R(t)^2; A = integral(RR, H,K)/2
# First example: cardioid. Numerically we have:
R = function(t) 1-sin(t); PLANE(-2,2, -3,1); polar(R, 0,2*pi, "blue")
areaPolar(R,0,2*pi,1000) # 4.712327
areaPolar(R,0,2*pi,2000) # 4.712373
areaPolar(R,0,2*pi,4000) # 4.712385
areaPolar(R,0,2*pi,8000) # 4.712388
areaPolar(R,0,2*pi,16000) # 4.712389
# With integration:
R=function(t) 1-sin(t); RR=function(t) R(t)^2; A=integral(RR, 0,2*pi)/2; A
# 4.712389
A/pi
# 1.5 A = 3/2*pi
#
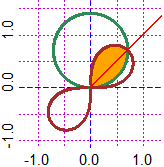
# Second example: the figure above right.
PLANE(-1.25,1.25, -1,1.5)
R1 = function(t) sqrt(2)*sin(t); R2 = function(t) sqrt(sin(2*t))
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
# I give color to the figure:
P=function(x,y) {r=sqrt(x^2+y^2); t=dirArrow1(0,0, x,y)*pi/180; r<=sqrt(sin(t*2)) & r<=sqrt(2)*sin(t)}
for(i in 1:8) FIGURE(P,0,1,0,1, "orange")
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
g = function(x) x; graph1(g, 0,2, "red")
polar(R1,0,pi/4, "blue"); polar(R2,pi/4,pi/2, "red")
# If the angle t changes from H to K:
# RR = function(t) R(t)^2; A = integral(RR, H,K)/2
# First example: cardioid. Numerically we have:
R = function(t) 1-sin(t); PLANE(-2,2, -3,1); polar(R, 0,2*pi, "blue")
areaPolar(R,0,2*pi,1000) # 4.712327
areaPolar(R,0,2*pi,2000) # 4.712373
areaPolar(R,0,2*pi,4000) # 4.712385
areaPolar(R,0,2*pi,8000) # 4.712388
areaPolar(R,0,2*pi,16000) # 4.712389
# With integration:
R=function(t) 1-sin(t); RR=function(t) R(t)^2; A=integral(RR, 0,2*pi)/2; A
# 4.712389
A/pi
# 1.5 A = 3/2*pi
#
# Second example: the figure above right.
PLANE(-1.25,1.25, -1,1.5)
R1 = function(t) sqrt(2)*sin(t); R2 = function(t) sqrt(sin(2*t))
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
# I give color to the figure:
P=function(x,y) {r=sqrt(x^2+y^2); t=dirArrow1(0,0, x,y)*pi/180; r<=sqrt(sin(t*2)) & r<=sqrt(2)*sin(t)}
for(i in 1:8) FIGURE(P,0,1,0,1, "orange")
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
g = function(x) x; graph1(g, 0,2, "red")
polar(R1,0,pi/4, "blue"); polar(R2,pi/4,pi/2, "red")
 R = function(t) ifelse(t < pi/4,R1(t),R2(t)); RR=function(t) R(t)^2; A=integral(RR,0,pi/2)/2; A
# 0.3926991
A/pi
# 0.25
pi/8
# 0.3926991
R = function(t) ifelse(t < pi/4,R1(t),R2(t)); RR=function(t) R(t)^2; A=integral(RR,0,pi/2)/2; A
# 0.3926991
A/pi
# 0.25
pi/8
# 0.3926991
 # Calcoliamo l'area della figura sopra al centro:
PIANO(0,1, 0,1)
f=function(x) x^2; g=function(x) x
grafico(f,0,1, "blue"); grafico(g,0,1,"red")
# La differenza tra l'area sotto al grafico di g e quella sotto a quello di f:
integrale(g,0,1)-integrale(f,0,1)
# 0.1666667
# Ovvero:
h = function(x) g(x)-h(x); integrale(h,0,1)
# 0.1666667 che equivale a:
frazio(integrale(h,0,1))
# 1/6 Questa è l'area cercata
#
# L'area della figura sopra a destra, tra le due curve
PIANO(0,4,-2,2)
f = function(x) sin(x); g = function(x) (x-2)^2
grafico(f,0,4, "red"); grafico(g,0,4, "blue")
soluz2(f,g,1,2)
# 1.064761
soluz2(f,g,2,3)
# 2.67242
h = function(x) f(x)-g(x)
integrale(h, soluz2(f,g,1,2), soluz2(f,g,2,3))
# 1.002636 Questa è l'area cercata
# poco più di un "quadretto"
#
# How to calculate areas enclosed by polar curves.
# Calcoliamo l'area della figura sopra al centro:
PIANO(0,1, 0,1)
f=function(x) x^2; g=function(x) x
grafico(f,0,1, "blue"); grafico(g,0,1,"red")
# La differenza tra l'area sotto al grafico di g e quella sotto a quello di f:
integrale(g,0,1)-integrale(f,0,1)
# 0.1666667
# Ovvero:
h = function(x) g(x)-h(x); integrale(h,0,1)
# 0.1666667 che equivale a:
frazio(integrale(h,0,1))
# 1/6 Questa è l'area cercata
#
# L'area della figura sopra a destra, tra le due curve
PIANO(0,4,-2,2)
f = function(x) sin(x); g = function(x) (x-2)^2
grafico(f,0,4, "red"); grafico(g,0,4, "blue")
soluz2(f,g,1,2)
# 1.064761
soluz2(f,g,2,3)
# 2.67242
h = function(x) f(x)-g(x)
integrale(h, soluz2(f,g,1,2), soluz2(f,g,2,3))
# 1.002636 Questa è l'area cercata
# poco più di un "quadretto"
#
# How to calculate areas enclosed by polar curves.

 # In the case of a circle of radius R I have that area A is pi*R^2.
# Generalizing, if R=R(t):
# In the case of a circle of radius R I have that area A is pi*R^2.
# Generalizing, if R=R(t):
 # If the angle t changes from H to K:
# RR = function(t) R(t)^2; A = integral(RR, H,K)/2
# First example: cardioid. Numerically we have:
R = function(t) 1-sin(t); PLANE(-2,2, -3,1); polar(R, 0,2*pi, "blue")
areaPolar(R,0,2*pi,1000) # 4.712327
areaPolar(R,0,2*pi,2000) # 4.712373
areaPolar(R,0,2*pi,4000) # 4.712385
areaPolar(R,0,2*pi,8000) # 4.712388
areaPolar(R,0,2*pi,16000) # 4.712389
# With integration:
R=function(t) 1-sin(t); RR=function(t) R(t)^2; A=integral(RR, 0,2*pi)/2; A
# 4.712389
A/pi
# 1.5 A = 3/2*pi
#
# Second example: the figure above right.
PLANE(-1.25,1.25, -1,1.5)
R1 = function(t) sqrt(2)*sin(t); R2 = function(t) sqrt(sin(2*t))
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
# I give color to the figure:
P=function(x,y) {r=sqrt(x^2+y^2); t=dirArrow1(0,0, x,y)*pi/180; r<=sqrt(sin(t*2)) & r<=sqrt(2)*sin(t)}
for(i in 1:8) FIGURE(P,0,1,0,1, "orange")
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
g = function(x) x; graph1(g, 0,2, "red")
polar(R1,0,pi/4, "blue"); polar(R2,pi/4,pi/2, "red")
# If the angle t changes from H to K:
# RR = function(t) R(t)^2; A = integral(RR, H,K)/2
# First example: cardioid. Numerically we have:
R = function(t) 1-sin(t); PLANE(-2,2, -3,1); polar(R, 0,2*pi, "blue")
areaPolar(R,0,2*pi,1000) # 4.712327
areaPolar(R,0,2*pi,2000) # 4.712373
areaPolar(R,0,2*pi,4000) # 4.712385
areaPolar(R,0,2*pi,8000) # 4.712388
areaPolar(R,0,2*pi,16000) # 4.712389
# With integration:
R=function(t) 1-sin(t); RR=function(t) R(t)^2; A=integral(RR, 0,2*pi)/2; A
# 4.712389
A/pi
# 1.5 A = 3/2*pi
#
# Second example: the figure above right.
PLANE(-1.25,1.25, -1,1.5)
R1 = function(t) sqrt(2)*sin(t); R2 = function(t) sqrt(sin(2*t))
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
# I give color to the figure:
P=function(x,y) {r=sqrt(x^2+y^2); t=dirArrow1(0,0, x,y)*pi/180; r<=sqrt(sin(t*2)) & r<=sqrt(2)*sin(t)}
for(i in 1:8) FIGURE(P,0,1,0,1, "orange")
polar(R1,0,2*pi, "seagreen"); polar(R2,0,2*pi, "brown")
g = function(x) x; graph1(g, 0,2, "red")
polar(R1,0,pi/4, "blue"); polar(R2,pi/4,pi/2, "red")
 R = function(t) ifelse(t < pi/4,R1(t),R2(t)); RR=function(t) R(t)^2; A=integral(RR,0,pi/2)/2; A
# 0.3926991
A/pi
# 0.25
pi/8
# 0.3926991
R = function(t) ifelse(t < pi/4,R1(t),R2(t)); RR=function(t) R(t)^2; A=integral(RR,0,pi/2)/2; A
# 0.3926991
A/pi
# 0.25
pi/8
# 0.3926991