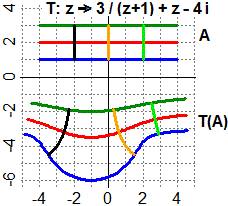
# An example of conformal map (see): z -> 3/(z+1)+z-4i
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
# Sketch the curves by approximating them with 100 segments
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) 3/(z+1)+z-4i
# The curves transformed by T
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)
 # Also try these transformations:
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) z^2/5+z-5i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)
#
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) 3/(z^3)+z-4i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)
# Also try these transformations:
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) z^2/5+z-5i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)
#
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) 3/(z^3)+z-4i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)

 # Also try these transformations:
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) z^2/5+z-5i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)
#
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) 3/(z^3)+z-4i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)
# Also try these transformations:
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) z^2/5+z-5i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)
#
PLANE(-6,6, -7,5)
x1 <- y1 <- x2 <- y2 <- x3 <- y3 <- x4 <- y4 <- x5 <- y5 <- x6 <- y6 <- NULL
c1 <- "blue"; c2 <- "red"; c3 <- "green4"; c4 <- "black"; c5 <- "orange"; c6 <- "green2"
i <- 1:101
x1[i] <- -4+8*(i-1)/100; y1[i] <- 1; segments(x1[i],y1[i],x1[i+1],y1[i+1],col=c1,lwd=3)
x2[i] <- x1[i]; y2[i] <- 2; segments(x2[i],y2[i],x2[i+1],y2[i+1],col=c2,lwd=3)
x3[i] <- x1[i]; y3[i] <- 3; segments(x3[i],y3[i],x3[i+1],y3[i+1],col=c3,lwd=3)
x4[i] <- -2; y4[i] <- 1+2*(i-1)/100; segments(x4[i],y4[i],x4[i+1],y4[i+1],col=c4,lwd=3)
x5[i] <- -0; y5[i] <- y4[i]; segments(x5[i],y5[i],x5[i+1],y5[i+1],col=c5,lwd=3)
x6[i] <- 2; y6[i] <- y4[i]; segments(x6[i],y6[i],x6[i+1],y6[i+1],col=c6,lwd=3)
T <- function(z) 3/(z^3)+z-4i
cu <- function(z1,z2,c) segments(Re(T(z1)),Im(T(z1)),Re(T(z2)),Im(T(z2)),col=c,lwd=3)
z1 <- x1[i]+1i*y1[i]; z2 <- x1[i+1]+1i*y1[i+1]; cu(z1,z2,c1)
z1 <- x2[i]+1i*y2[i]; z2 <- x2[i+1]+1i*y2[i+1]; cu(z1,z2,c2)
z1 <- x3[i]+1i*y3[i]; z2 <- x3[i+1]+1i*y3[i+1]; cu(z1,z2,c3)
z1 <- x4[i]+1i*y4[i]; z2 <- x4[i+1]+1i*y4[i+1]; cu(z1,z2,c4)
z1 <- x5[i]+1i*y5[i]; z2 <- x5[i+1]+1i*y5[i+1]; cu(z1,z2,c5)
z1 <- x6[i]+1i*y6[i]; z2 <- x6[i+1]+1i*y6[i+1]; cu(z1,z2,c6)