Il ragionamento statistico per saper discernere
http://macosa.dima.unige.it/R/ConIstat
http://macosa.dima.unige.it/R
Lo studio delle incertezze nell'insegnamento della fisica

• L'analisi statistica degli errori casuali • Leggi di distribuzione nella fisica sperimentale • La statistica per investigare la relazione matematica tra due grandezze fisiche

 0    Premessa
   A   Come usare il materiale
   B   I programmi
   C   La scuola elementare
   D   La scuola media inferiore
   E   I libri di testo
   F   In rete (WolframAlpha)
 1   L'analisi statistica degli errori casuali
   A   Misure a bassa sensibilità
   B   Misure ad alta sensibilità
 2   Leggi di distribuzione nella fisica sperimentale
   A   Statistica descrittiva
   B   Il teorema limite centrale
 3   La statistica per investigare la relazione matematica tra due grandezze fisiche
   A   Premessa
   B   Come caricare e analizzare file di dati
 4   Riferimenti

0 - Premessa
A - Come usare il materiale.   Qui è presente grosso modo quanto verrà esposto.  Svolgeremo anche varie attività con R. In questo caso occorrerà copiare di volta in volta da qui in R le righe scritte in rosso, dalla prima all'ultima riga inizianti con "#" (le righe inizianti con # sono dei "commenti", che R legge senza interpretare).  Gli esempi saranno riferiti ad attività fattibili in classe, in cui, ovviamente, come suggeriscono i programmi, la statistica si intreccia con altre aree matematiche e con la fisica, e con altre discipline. Su ciò torneremo.  Gli esempi saranno semplici, ma cercheranno di mettere in luce alcune attenzioni particolari che occorre prestare nell'insegnamento: è facile fare un uso acritico degli strumenti statistici, specie nell'ambito delle scienze fisiche.  Ci saranno anche dei link ad "approfondimenti", che chi vuole poi potrà esaminare.

B - I programmi.   Partiamo con uno spot.  Clicca qui e lascia scorrere le immagini, fino a che ritorna l'immagine iniziale.  Quindi chiudi pure la finestra  (fai lo stesso anche dopo, con le altre nuove finestre che vengono aperte;  non fare lo stesso con i link che rinviano a punti diversi di questo documento: puoi tornare indietro col tasto ←).
    Questo spot si riferisce ad attività svolgibili tra l'ultimo anno di asilo e la prima elementare. La statistica di fatto ha costituito la prima attività matematica dell'uomo: invece degli istogrammi a crocette c'erano le tacche tracciate su un tronco d'albero o su una roccia, ma la sostanza non cambia.
    Nella scuola italiana la statistica è arrivata molto tardi. È comparsa prima per l'insegnamento della fisica e poi ha fatto il suo ingresso nei programmi della media inferiore, nel 1979.  Ecco come.
    Sono chiarissime le indicazioni di non dare definizioni "esplicite" del concetto di probabilità (come quella, buffa, "(n. casi favorevoli)/(n. dei casi)", che si trova su molti libri),  di partire da considerazioni statistiche,  di dare peso alle rappresentazioni grafiche.  Nella premessa dei programmi c'è scritto che la statistica e la probabilità non devono essere insegnate come argomenti a parte ma devono essere intrecciate alle altre aree della matematica e alle altre discipline. Su quest'ultimo aspetto, collegato al tema dell'incontro di oggi, ritorneremo.
    Poco dopo la statistica e il calcolo delle probabilità hanno fatto il loro ingresso ufficiale nei programmi degli altri ordini scolastici, nelle scuole elementari e nelle scuole medie superiori.  Ma, di fatto, sono entrati nei curricoli scolastici solo di pochi insegnanti, e quasi mai rispettando le indicazioni di non farne un argomento a sé. Anche su questo aspetto torneremo dopo.
    Un primo passo per la comprensione di ciò che è accaduto può essere leggere le indicazioni presenti nei vecchi programmi (di 60 e più anni fa) dei licei.
    Anche le indicazioni dei vecchi programmi non sono state, mediamente, rispettate.
    È questo "non rispetto" che è all'origine dei ritardi nell'introduzione a scuola dei temi statistico-probabilistici. E tutto ciò, come vedremo, si connette al tema oggetto dell'incontro odierno.
    Faremo, dunque, qualche flash anche sulle cose che dovrebbero essere fatte nei livelli scolastici precedenti.

C - La scuola elementare.   Vediamo qualche spot, usando R. Intanto rivediamo alcuni comandi a partire dalle cose più semplici.

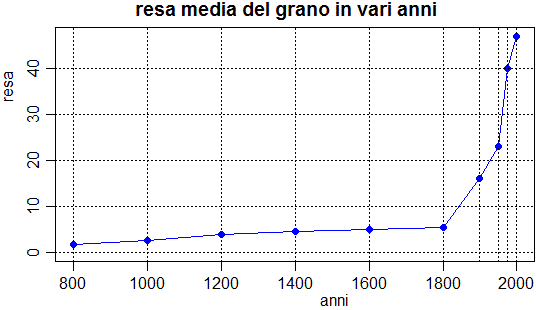
• Qui traccio un grafico (relativo alla evoluzione nel tempo di un dato medio) che appare su una finestra diversa da quella del testo. Col mouse posso spostare e ridimensionare la finestra grafica. Ovviamente, nella scuola elementare, queste cose non vanno fatte con R!

# Un esempio:
anni <- c(800,1000,1200,1400,1600,1800,1900,1950,1975,2000)
resa <- c( 1.7, 2.5, 4.0, 4.5, 5.0, 5.5, 16, 23, 40, 47)
plot(anni, resa, ylim=c(0,max(resa)), pch=19, col="blue")
abline(v=axTicks(1), h=axTicks(2),lty=3)
abline(v=c(1900, 1950, 1975),lty=3)
lines(anni,resa,col="blue")
title("resa media del grano in vari anni")
# Ho messo in  anni  e in  resa  le "x" e le "y", ho tracciato i pallini
# pieni (pch=19 - se non mettevo questo comando tracciavo solo i contorni)
# Con ylim o scelto l'intervallo delle y (potevo omettere ylim, pch, col)
# Ho tracciato rette (abline) tratteggiate (lty=3) facendo scegliere al
# programma (con axTicks) automaticamente le coordinate (altrimenti le
# potevo specificare, come ho fatto nella riga successiva)
# Poi con lines ho congiunto i pallini

[vedi qui per approfondimenti]

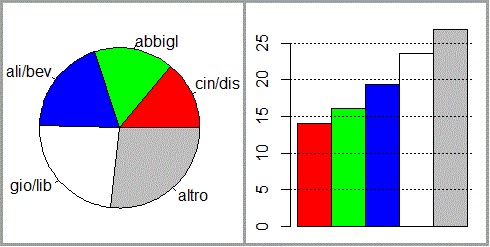
• Ecco la rappresentazione di una ripartizione percentuale.

# Un altro esempio (chiudi la finestra grafica precedente):
# esiti d'una indagine sulle spese di giovani tra i 14 e i 19 anni 
nomi <- c("cin/dis","abbigl","ali/bev","gio/lib","altro")
dati <- c(13, 15, 18, 22, 25)
co <- c("red","green","blue","white","grey")
pie(dati,col=co,nomi)
dev.new()
barplot(dati/sum(dati)*100, space=0,col=co)
abline(h=c(5,10,15,20,25,30),lty=3)
# dev.new() ha aperto una nuova finestra grafica, in modo che posso vedere
# entrambi i grafici. Le finestre aperte le vedo azionando il menu Windows.
# Le posso spostare e ridimensionare. pie fa un diagramma a torta, barplot
# un diagramma a barre, space=0 pone = 0 lo spazio tra le colonne
# Potevo non assegnare io i colori (col) e non mettere nomi.

[vedi qui per approfondimenti]

• Abbiamo visto esempi di "storia" e di "costume". Vediamo un esempio di "lingua": vedi.

• Ecco come "determinare" le percentuali, con procedimenti di calcolo e di arrotondamento alla portata dei bambini: vedi.

• Lo studio statistico di un dado costruito col cartoncino, di quelli che i bambini trovano in edicola. Qual è la probabilità che esca una particolare faccia? (qui vediamo l'esempio simulato; in classe può essere realizzato praticamente)  vedi  (è un tipico "vaccino" contro cose buffe come le definizioni "casi/casi").

D - La scuola media inferiore.   Ora lo studio può essere più formalizzato. Si possono cominciare ad usare mezzi di calcolo (in 2ª o 3ª anche R, il cui uso è più semplice di quello di un foglio di calcolo). Due spot legati ad attività svolte in classi di 2ª media (da qui sono poi partite attività legate al tema "genetica", che sono state affrontate utilizzando anche concetti probabilistici).

• In una classe di 2ª media (docente: Nadia Zamboni) gli alunni hanno raccolto molti semi di fava e ne hanno misurato la lunghezza disponendoli su carta millimetrata e arrotondando le misure al mezzo millimetro più vicino. Le misure le hanno lette da fotografie che hanno fatto dei semi, come la seguente:

# Ecco le misure che hanno ottenuto:
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
stem(fave)
# Chiudo la finestra grafica precedente (con un comando invece che col mouse)
dev.off()
hist(fave)
# Traccio il boxplot su una pagina nuova, poi spostabile e ridimensionabile
dev.new()
boxplot(fave, horizontal=TRUE, col="yellow", range=0)
# Ho messo opzioni per cambiarne la vista, ma potevo mettere solo boxplot(fave)

#
#  The decimal point is 1 digit(s) to the left of the |
#
# 10 | 00
# 11 | 
# 12 | 
# 13 | 0055
# 14 | 000000000000000000000055
# 15 | 0000000000000000000000005555555555555555
# 16 | 0000000000000000000000000000000000000000005555555555555555555555
# 17 | 0000000000000000000000000000000000000000005555555555555555555555
# 18 | 00000000000000000000000000000055555555
# 19 | 000000000000000055
# 20 | 00
# 21 | 
# 22 | 55
# 23 | 00

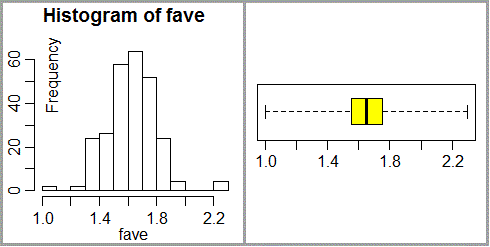
[vedi qui e qui per approfondimenti sugli "stem-and-leaf" e sui "box-plot"].

• In un'altra classe (docente: Anna Chiozzi) gli alunni hanno raccolto molti semi di basilico e ne hanno studiato la lunghezza. Dato che le loro dimensioni erano molto piccole, ne hanno misurato la lunghezza con un particolare microscopio in cui la luce viene trasmessa dall'alto invece che dal basso [vedi], dotato di un dispositivo che consente di registrare le immagini su un computer e di effettuare elettronicamente misurazioni di lunghezza.  Nel caso precedente erano misure a bassa sensibilità, queste sono ad alta sensibilità. (su questi concetti ritorneremo)

# Ecco le misure che hanno ottenuto:
semi <- c(
1.996646,2.427837,2.002445,2.032486,2.440977,2.179811,1.827547,2.122749,2.273763,
2.237457,2.234695,2.416860,1.855254,2.141668,2.274085,2.148191,2.188731,2.279401,
1.861674,2.148191,2.277117,1.907743,2.151697,2.149251,1.874470,2.149251,2.279401,
1.885252,2.309115,2.479710,1.883268,2.151697,2.302933,1.979976,2.353246,2.231072,
1.885252,2.176491,2.309115,1.861674,2.274085,2.336312,1.891458,2.178452,2.335834,
2.072091,2.302933,2.196575,1.907743,2.179811,2.336312,2.141668,2.273763,2.194292,
1.943342,2.181266,2.339914,2.348716,2.574592,1.967000,2.188731,2.348716,2.208185,
2.277117,1.975734,2.194292,2.353246,1.943342,2.238444,1.979976,2.196575,2.395220,
2.098704,2.482356,1.996646,2.204940,2.406590,2.204940,2.458355,2.002445,2.205823,
2.416860,1.883268,2.667822,2.015793,2.208185,2.427837,2.015793,2.457101,2.016699,
2.224770,2.440977,1.855254,2.395220,2.032486,2.226911,2.457101,2.052005,2.176491,
2.033379,2.231072,2.458355,2.104753,2.178452,2.045551,2.232692,2.459751,2.335834,
2.339914,2.052005,2.234695,2.479710,2.122749,2.033379,2.069424,2.237457,2.482356,
1.967000,1.975734,2.072091,2.238444,2.574592,2.267303,2.205823,2.098704,2.267303,
2.667822,2.232692,2.226911,2.104753,1.891458,2.406590,2.045551,1.827547,2.069424,
2.459751,1.874470,2.181266,2.224770,2.016699,2.602342,1.980298,2.414356,2.156164,
1.944474,2.176403,2.381037,2.665530,2.282354,1.971069,2.178466,2.389039,2.403857,
2.176403,1.980298,2.222064,2.400560,2.441692,2.256341,2.005266,2.233202,2.403857,
2.400560,2.301457,2.047079,2.256341,2.414356,2.279626,2.222064,2.063478,2.257275,
2.441692,2.389039,2.293673,2.073464,2.264273,2.441809,2.663396,2.063478,2.075890,
2.279626,2.501192,2.575395,2.264273,2.080611,2.282354,2.524316,1.944474,2.112226,
2.097085,2.288252,2.575395,2.047079,2.178466,2.112226,2.293673,2.602342,2.073464,
2.299742,2.141965,2.299742,2.654032,2.142679,2.305893,2.142679,2.301457,2.663396,
2.075890,2.144709,2.144709,2.305893,2.665530,2.080611,2.288252,2.156164,2.345941,
2.739415,2.163349,2.257275,2.161602,2.364831,2.762354,2.141965,2.161602,2.163349,
2.368598,2.005266,2.097085,1.971069,2.381037,2.345941,2.233202,2.739415,2.524316,
2.762354,2.364831,2.501192,2.654032,2.368598,2.441809)
stem(semi)
# Chiudo la finestra grafica precedente
dev.off()
hist(semi)
# Traccio il boxplot su una pagina nuova, poi spostabile e ridimensionabile
dev.new()
boxplot(semi, horizontal=TRUE, col="yellow", range=0)
# Non ci soffermiamo troppo su questi esempi. Vediamo solo un altro aspetto.

# The decimal point is 1 digit(s) to the left of the |
#
# 18 | 33
# 18 | 666677889999
# 19 | 114444
# 19 | 7777888888
# 20 | 00001122223333
# 20 | 555555667777778888
# 21 | 000000112244444444
# 21 | 5555556666668888888888889999
# 22 | 00001111222233333333334444
# 22 | 666666777777888888889999
# 23 | 0000001111444444
# 23 | 55555566778899
# 24 | 00000011112233444444
# 24 | 6666668888
# 25 | 0022
# 25 | 7788
# 26 | 00
# 26 | 55667777
# 27 | 44
# 27 | 66

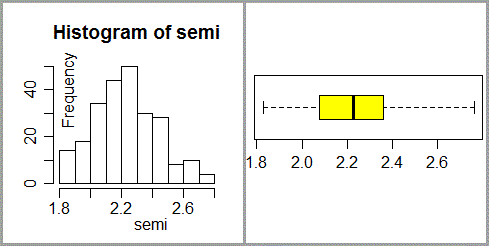
• Le lunghezze dei semi hanno andamento "gaussiano", ma i volumi no! Questo flash è riferito, ovviamente, a cosa affrontabili nelle scuole superiori. Su questi aspetti torneremo.

# Chiudo la finestra grafica precedente
dev.off()
# faccio l'istogramma delle densità di frequenza (l'area totale è 1)
hist(semi,probability=TRUE)
# sovrappongo la gaussiana - o distrib. normale (vedremo dopo come abbiamo fatto)
z <- function(x) dnorm(x,mean=mean(semi),sd=sd(semi)); curve(z,add=TRUE)
dev.new()
# faccio le stesse cose per i volumi, stimandoli facendo il cubo delle lunghezze
# dei semi che avranno una distribuzione simile dei volumi effettivi
volumi <- semi^3
hist(volumi,probability=TRUE)
z <- function(x) dnorm(x,mean=mean(volumi),sd=sd(volumi)); curve(z,add=TRUE)
# I cubi non hanno andamento gaussiano! Sono poche le grandezze con
# andamento gaussiano. Vedremo, poi, il ruolo della gaussiana.

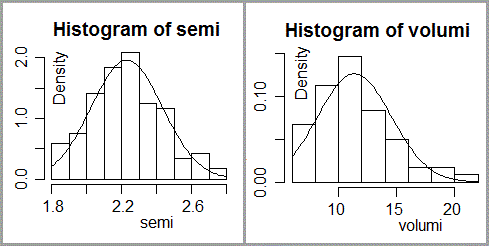
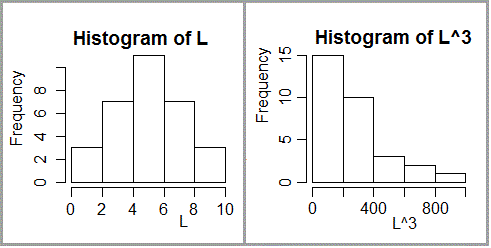
Vediamo, solo, come "vaccino" che dovrebbe rimanere impresso, un esempio semplice: la distribuzione delle lunghezze dei lati di un po' di cubetti e quella dei loro volumi. Copiamo le righe seguenti a scatola nera (poi potrete tornarci dopo):

#
dev.off()
L <- c(1,rep(2,2),rep(3,3),rep(4,4),rep(5,5),rep(6,6),rep(7,4),rep(8,3),rep(9,2),rep(10,1))
dev.new(xpos=600); hist(L)
dev.new(xpos=300);  hist(L^3)
#

E - I libri di testo.   Abbiamo accennato allo stato della scuola italiana. Non poche responsabilità hanno i libri di testo, che non c'è alcun obbligo di adottare, e che non hanno mai rispettato le indicazioni dei programmi (tranne pochi casi: i libri di Prodi, Villani, Lombardo Radice, …). Su questo aspetto non ci fermiamo [Chi fosse interessato può dare una occhiata qui - vedi gli esempi riferiti al calcolo delle probabilità, anche nella pagina successiva].

F - In rete.   Gli esempi che vedremo saranno svolti con R, che consente di affrontare, gratuitamente e da qualunque piattaforma, ogni attività matematica di base (non solo statistica).  Altri argomenti, sia di statistica che di ogni area matematica, e non solo, sono affrontabili con WolframAlpha (vediamo qui qualche esempio legato alla statistica; soffermiamoci solo, cliccando "=", sul primo esempio [altri esempi li puoi trovare qui]).  Una buona presentazione dei vari argomenti di statistica può essere trovata in WikiPedia (versione inglese!!!) [dove si trova anche una breve presentazione di R].

1 - L'analisi statistica degli errori casuali
A - Misure a bassa sensibilità.   Gli strumenti graduati sono in genere costruiti in modo che l'ampiezza di una divisione corrisponda alla sensibilità dello strumento (la minima variazione della grandezza misurata che fa variare il valore indicato dallo strumento).  Un comune orologio al quarzo di tipo digitale che visualizza i centesimi di secondo è uno strumento a bassa sensibilità:  se leggo 3.27 ciò significa che il tempo è compreso tra 3.27 sec e 3.28 sec, cioè che [3.27,3.28], in genere indicato 3.275±0.005, è un intervallo di indeterminazione certo.  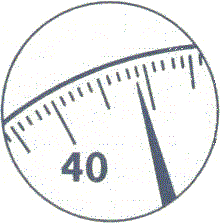Anche un usuale termometro è a bassa sensibilità; le misure, in questo caso, non sono da approssimare per difetto, come nel caso del cronometro, ma da arrotondare (nel caso raffigurato è indicato che l'errore può andare da −1° ad 1°, ovvero che la precisione è di 1°); lo stesso accade, in genere, per le bilance o per i tachimetri (la figura a destra indica 49±0.5 km/h).

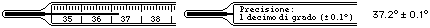Le scale spesso non sono lineari, e quindi le tacche non sono equidistanziate [vedi]. Negli esempi seguenti le scale sono lineari.

• Un primo esempio.

# Chiudo la finestra grafica precedente (se era ancora aperta)
dev.off()
# So che un cerchio ha raggio di 5.1 ± 0.1 cm. Posso calcolarne l'area con
r1 <- 5.1-0.1; r2 <- 5.1+0.1; pi*r1^2; pi*r2^2
# [1] 78.53982
# [1] 84.94867
# o con
r <- 5.1 + c(-0.1, 0.1); pi*r^2
# [1] 78.53982  84.94867
# Ottengo  78.53982  84.94867
# Nota: la variabile r contiene una coppia; battendo r ho il complesso dei due
# valori, battendo r[1] e r[2] li posso avere singolarmente:
r; r[1]; r[2]
# [1] 5.0  5.2
# [1] 5
# [1] 5.2
# Nota: se V è una sequenza, V[1], V[2], ... ne sono gli elementi.

Posso esprimere la soluzione, in cm², con [78.5, 85.0]. Osserviamo che non avrebbe molto senso calcolare 5.1²·π = 81.71282 ed esprimere l'area con 81 cm² (come spesso viene fatto nei libri di fisica!).

• Ricordo che usando i tasti freccia ^ e v posso rivedere e riusare o modificare comandi già impiegati. Proviamo a farlo.

• Un altro esempio. Calcolo l'area dell'ellisse di semiassi di 5.1±0.1 cm e 7.6±0.1 cm.

# Se non tenessi conto delle precisioni farei
r1 <- 5.1; r2 <- 7.6; A <- pi*r1*r2; A
# [1] 121.7681
# ottenendo 121.7681. Vediamo come fare il calcolo correttamente:
r1 <- 5.1 + c(-0.1, 0.1); r2 <- 7.6 + c(-0.1, 0.1)
# Inizializzo la variabile A in cui metto i 4 valori:
A <- NULL; for(i in 1:2) for(j in 1:2) A <- c(A, pi*r1[i]*r2[j])
A; min(A); max(A)
# [1] 117.8097  120.9513  122.5221  125.7894
# [1] 117.8097
# [1] 125.7894
# Prendo [117, 126] come intervallo di indeterminazione.
# NULL serve a inizializzare la variabile A, il doppio ciclo for aggiunge
# via via ad A i vari prodotti tra gli estremi dei due intervalli, min e
# max ne determinano gli estremi, m:n è la sequenza degli interi da m ad n

• Invece che usare min e max potrei prendere direttamente il prodotto dei minimi e quello dei massimi. Ma nel caso della divisione avrei dovuto procedere diversamente (min/max, max/min). Un esempio.
In una pubblicazione dell'ISTAT trovo che il Lussemburgo nel 1990 aveva 381 mila abitanti, con densità di 147 ab./km² e superficie S di 3 mila km². Come trovare S più precisamente?

# Tengo conto che i dati sono arrotondati:
P <- c(380.5,381.5)*1e3; D <- c(146.5,147.5); S <- NULL
for(i in 1:2) for(j in 1:2) S <- c(S, P[i]/D[j]); min(S); max(S)
# [1] 2579.661
# [1] 2604.096
# 2579.6 <= S <= 2604.1, o S = 2590±15

• Ancora un esempio. Un auto impiega 36 s per percorrere 1000 m. So che il tempo è troncato ai secondi e che lo spazio è arrotondato ai metri, con la precisione di 1 m. Qual'era la velocità media dell'auto? Mentalmente trovo l'ordine di grandezza; è facile: 60*60/36 = 100 km/h

# I calcoli:
t <- c(36,37)/60/60; s <- c(999,1001)/1000
v <- NULL; for(i in 1:2) for(j in 1:2) v <- c(v, s[i]/t[j])
min(v); max(v); (max(v)+min(v))/2; (max(v)-min(v))/2
# [1] 97.2
# [1] 100.1
# [1] 98.65
# [1] 1.45
# Posso concludere che v = 98.6 ± 1.5 km/h

Perché non è un intervallo centrato in 100?

• Un tempo, mezzo secolo fa, quando non esistevano le calcolatrici, si usavano, in fisica, per il prodotto e la divisione, delle regolette di questo tipo:  la precisione relativa è la somma delle precisioni relative (sono approssimazioni deducibili attraverso opportuni sviluppi in serie, hanno ancora la loro valenza applicativa in alcuni casi particolari, come i laureati in fisica probabilmente sanno).  Nei libri di testo di fisica sono, purtroppo, spesso ancora presenti, ma non sono comode neanche per stime rapide in assenza di mezzi di calcolo. È migliore la seguente regoletta pratica per il calcolo mentale:
nel caso di una moltiplicazione o divisione tra più numeri arrotondo il risultato al numero di cifre pari al più piccolo tra i numeri di cifre significative dei vari termini che ho moltiplicato o diviso.
Nel caso precedente avrei ottenuto 3600/36.5 = 98.63014, arrotondabile a 99 (a 2 cifre, come 36, mentre lo spazio era approssimato a 4 cifre); ho usato 36.5 e non 36 in quanto il dato era troncato, ossia stava tra 36 e 37.

B - Misure ad alta sensibilità.   Consideriamo, ora, le misure ad alta sensibilità.

• Prendiamo in esame uno strumento semplice, di cui potrebbe essere dotata facilmente qualunque scuola, e che ha una notevole rilevanza sociale:  il reflettometro, per la determinazione del tasso glicemico del sangue (viene depositata una goccia di sangue su una striscetta, che viene inserita nello strumento; questo, mediante un opportuno dispositivo ottico, effettua il rilevamento ed esprime il valore in mg/dl - (vedi).
In dotazione è presente (per verificare il corretto funzionamento dell'apparecchio) una striscia di controllo trattata in modo da avere caratteristiche corrispondenti a quelle di una goccia di sangue con un certo tasso glicemico.
Effettuo più volte la misurazione del "tasso glicemico" della striscia di controllo. Non ottengo sempre lo stesso valore: è un classico esempio di misura ad alta sensibilità: pur essendo costante il tasso glicemico della striscia, ad ogni rilevamento ottengo un valore diverso. Quale precisione devo associare ad un rilevamento fatto con questo strumento?

tasso gl.	74	75	76	77	78	79	80	81
frequenza	1	2	4	15	33	23	10	01

# Vediamo come inserire questi dati
# Uso la funzione rep di cui è evidente il significato:
T <- c(74,rep(75,2),rep(76,4),rep(77,15),rep(78,33),rep(79,23),rep(80,10),81)
# Se voglio vederne il significato posso battere:
help(rep)
#

# Per una conferma visualizzo i valori e ne calcolo la quantità:
T; length(T)
#  [1] 74 75 75 76 76 76 76 77 77 77 77 77 77 77 77 77 77 77 77 77 77 77 78
# [24] 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78 78
# [47] 78 78 78 78 78 78 78 78 78 79 79 79 79 79 79 79 79 79 79 79 79 79 79
# [70] 79 79 79 79 79 79 79 79 79 80 80 80 80 80 80 80 80 80 80 81
# [1] 89
#

Che fare? Come potremmo associare una precisione a questo strumento?

# Visualizzo i dati con uno stem-and-leaf
stem(T)
# The decimal point is at the |
# 74 | 0
# 75 | 00
# 76 | 0000
# 77 | 000000000000000
# 78 | 000000000000000000000000000000000
# 79 | 00000000000000000000000
# 80 | 0000000000
# 81 | 0
# Facciamoci un'idea "numerica" di come sono distribuiti i dati (minimo e
# massimo, 1º e 3º quartile, 2º quartile o mediana, media):
summary(T)
#   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#  74.00   78.00   78.00   78.15   79.00   81.00
# Facciamo l'istogramma:
hist(T)
#

R, in assenza di indicazioni, sceglie automaticamente gli intervalli. L'istogramma ottenuto ci dà un'idea di come sono distribuiti i dati. Ma, in questo caso, conviene scegliere noi gli intervalli (per altro come mediana ci viene visualizzato 78, che non corrisponde affatto alla ascissa per cui passa la retta verticale che divide a metà l'istogramma).  Vediamo come, e perché.

# Chiudo la finestra e ne apro un'altra. Ne metto pure dimensioni e posizione
dev.off()
dev.new(width=4,height=5, xpos=300,ypos=10)
hist(T, col="yellow"); abline(h=axTicks(2),lty=3)
dev.new(width=4,height=5, xpos=600,ypos=10)
hist(T,seq(73.5,81.5, 1), probability=TRUE, col="yellow"); abline(h=axTicks(2),lty=3)
# ( invece di probability=TRUE avrei potuto usare freq=FALSE )
# Che cosa ho cambiato?

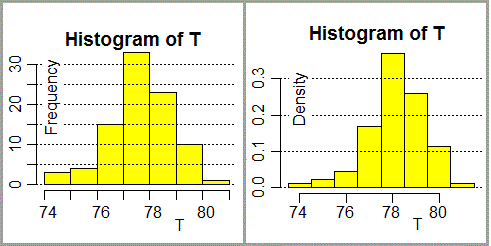
A parte il fatto che nel secondo istogramma ho rappresentato le frequenze relative invece che quelle assolute, il fatto rilevante è che ho tenuto conto che i dati erano arrotondati agli interi, per cui, col comando seq (che nel caso di questo esempio genera i numeri che vanno da 73.5 e non superano 81.5, e vanno avanti di 1 in 1), ho scelto gli intervalli centrati nei valori interi, come si vede nei grafici ottenuti. L'istogramma, altrimenti, mi darebbe informazioni distorte dei dati (questo è un errore abbastanza grave e, purtroppo, piuttosto diffuso).
Notiamo che nel caso della prima rappresentazione, con la scelta automatica degli intervalli, R ha scelto per essi estremi interi e ha collocato automaticamente i dati che stanno alle estremità negli intervalli più interni, per rendere più "efficace" la rappresentazione (74 e 75 li ha rappresentati in uno stesso intervallo).  La cosa è spesso utile ma, ovviamente, non ha molto senso nel caso di valori arrotondati come questi, e creerebbe confusioni negli alunni.

Per vedere meglio l'andamento:

# traccio anche la poligonale corrispondente:
x <- hist(T,seq(73.5,81.5),plot=FALSE)$mids
y <- hist(T,seq(73.5,81.5),plot=FALSE)$density
points(x,y); lines(x,y,lty=3)
# mids sono i centri degli intervalli

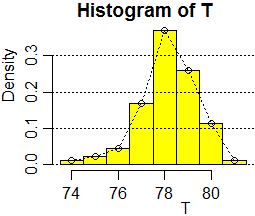
È evidente che non è una gaussiana. Ben poche misure fisiche hanno andamento gaussiano (come abbiamo già osservato in precedenza).  Perché è importante la gaussiana? Ci torneremo fra un po'.
Altro aspetto. Il valor medio (o valore atteso) che abbiamo ottenuto, 78.14, è il valor medio della variabile casuale "esito di un rilevamento per la striscia di controllo". Il valore vero del tasso glicemico della striscia di controllo non è tuttavia questo valore medio.
Questo è un problema che riguarda tutte le misure fisiche, ed è legato alla forma che assume l'istogramma dei rilevamenti.
Non approfondiamo questo aspetto. Per ora ci limitiamo al fatto che in base alle uscite dobbiamo scegliere un intervallo per rappresentare il tasso glicemico. Accontentiamoci di prendere 78, ossia 78±0.5.
Osserviamo, per inciso, un altro aspetto: i valori ottenuti variano da 74 ad 81.  Quindi il valore che si ottiene con una singola misura può variare anche di 4 dal valor medio.  Posso dunque assumere pari a 5 la precisione di un reflettometro:  se ottenendo 92 come valore, posso dire che il tasso glicemico è  92 ± 5 (mg/dl).
Il caso del reflettometro è un caso in cui, a parte quello che abbiamo fatto con la striscia di controllo, non ha senso ripetere la misura molte volte, fare la media, …. Diverso è il caso di altre misure ad alta sensibilità, come vedremo.

• Un secondo esempio (la misura a mano con un cronometro dell'intervallo di tempo di 1 secondo scandito con un altro cronometro). Lo usiamo come esempio per rifletterci su (ovviamente sappiamo che il valore è 1 s!).
Carichiamo un file da rete. Vediamo come lo si può fare da R.

# Leggo alcune righe (ad es. 4) di un file in rete (ne leggo poche in quanto
# il file può essere lunghissimo, ad es. contenere qualche migliaia di dati):
readLines("http://macosa.dima.unige.it/R/t-sec.txt",n=4)
# [1] "# misure (troncate ai centesimi di sec) della durata di 1 s cronometrata a mano"
# [2] "111"
# [3] "103"
# [4] "109"
# Vedo che sono singoli dati interi e che c'è una riga da saltare. Sono separati
# da "aCapo"; li leggo col comando "scan" (se fossero separati da, ad es., ";"
# aggiungerei , sep=";" )
dati <- scan("http://macosa.dima.unige.it/R/t-sec.txt", skip=1)
# Read 47 items
# Il comando  str  visualizza la struttura di oggetti. Lo uso per esaminare  dati
str(dati)
#  num [1:47] 111 103 109 97 99 110 99 103 109 106 ...
# sono 47 dati. I dati sono troncati agli interi. Per fare valutazioni corrette
# devo avere dati arrotondati: aggiungo 1/2
DATI <- dati+1/2
summary(DATI)
#   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
#  68.50   96.50   98.50   99.86  108.00  129.50
#

Traccio l'istogramma.

# Chiudiamo tutte le finestre aperte.  Potrei farlo a mano,
# ma, per curiosità, facciamo tutto in un colpo, col comando:
dev.off(dev.list())
dev.new()
hist(DATI,right=FALSE,seq(65,135,10))
# L'istogramma è abbastanza simmetrico.

In effetti ha senso ritenere che il rilevamento manuale dia luogo a scostamenti positivi e negativi dal valore "vero" che si compensano. Aumentando il numero dei rilevamenti vedremmo più chiaramente questa simmetria.
Nell'ipotesi che le misure si distribuiscano in modo tendenzialmente simmetrico intorno alla misura vera, possiamo assumere la media come stima della misura vera (infatti se la funzione densità ha grafico simmetrico, l'asse di simmetria deve intersecare l'asse orizzontale in corrispondenza della media).
Come valutare la precisione con cui la media approssima la misura vera?
Possiamo assumere il triplo della "deviazione standard della media". Su questo torneremo. Ecco come farne il calcolo con R.

# La d.s. della media è la d.s. divisa per la √ della numerosità dei dati
3*sd(DATI)/sqrt(length(DATI))
# [1] 4.74949
#

Dati i valori ottenuti (99.86 per la media e 4.75 per 3σ/√n) posso dire (con pratica "certezza", come vedremo) che il tempo è 100 ± 5 cs.

2 - Leggi di distribuzione nella fisica sperimentale
A - Statistica descrittiva.   Consideriamo qualche semplice problema di fisica, soffermandoci brevemente su come possono essere esaminati i dati.

• Un primo esempio. La verifica (o la scoperta …) della terza legge di Keplero [vedi su wolframalpha: "The square of the orbital period of a planet is directly proportional to the cube of the semimajor axis of its orbit"]

# verifica della terza legge di Keplero
S <- c("mercurio","venere","terra")       # nomi satelliti
a <- c(5.791e10, 1.082e11, 1.496e11)      # semiassi magg.
p <- c(87.969, 224.632, 365.256)*3600*24  # periodi riv.
for(i in 1:3) print(c(S[i],(p^2/a^3)[i]), quote=FALSE)
# [1] mercurio             2.97458306005555e-19
# [1] venere               2.97364383632925e-19
# [1] terra                2.97459211147732e-19
# Ho messo in S delle stringhe che poi, con "quote=FALSE", stampo senza virgolette

• Un secondo esempio.  Tre classi misurano più volte la durata di dieci oscillazioni di un pendolo.  Sono misurazioni ad alta sensibilità.  I dati sono messi in rete nei file A.txt, B.txt e C.txt; in A sono inseriti uno per riga, in B separati da spazi bianchi, in C da virgole, ma potrebbero essere separati anche da altri caratteri. Se non so come sono registrati i dati posso esaminarli con:

# Visualizzo poche righe dei file:
readLines("http://macosa.dima.unige.it/R/A.txt",n=3)
# [1] "# durata di 10 oscillazioni dello stesso pendolo fatta dal gruppo 1 di studenti"
# [2] "10.53"
# [3] "10.79"
readLines("http://macosa.dima.unige.it/R/B.txt",n=3)
# [1] "# durata di 10 oscillazioni dello stesso pendolo fatta dal gruppo 2 di studenti"
# [2] "10.56 10.49 10.22 10.43 10.7 10.61 10.45 10.59 10.48 10.53 10.51 9.96 10.46 10.21"
# [3] "10.46 10.52 10.48 11.05 10.27 10.44 10.71 10.44 10.25 10.37 10.52 10.49 10.71"
readLines("http://macosa.dima.unige.it/R/C.txt",n=3)
# [1] "# durata di 10 oscillazioni dello stesso pendolo fatta dal gruppo 3 di studenti"
# [2] "10.08,10.26,10.57,10.34,10.73,10.23,10.09,10.9,10.82,10.3,10.34,10.58,10.41"
# [3] "10.49,10.53,10.52,10.43,10.77,10.58,10.9,10.52,10.56,10.89,10.46,10.64,10.58,10.46"
# Ho la conferma di come sono separati i dati

Carico i dati in tre variabili col comando scan specificando (se diverso da ACapo e da Spazio) il separatore. Nei file c'è una riga di commenti; la salto con skip. Con str ne visualizzo sinteticamente la struttura.

# Ecco i dati:
A <- scan("http://macosa.dima.unige.it/R/A.txt", skip=1); str(A)
# Read 68 items
#  num [1:68] 10.5 10.8 10.4 10.5 10.7 ...
B <- scan("http://macosa.dima.unige.it/R/B.txt", skip=1)
# Read 82 items
C <- scan("http://macosa.dima.unige.it/R/C.txt", sep=",", skip=1)
# Read 63 items
# Li riunisco in una variabile T.
T <- c(A,B,C); c(length(A),length(B),length(C),length(T))
# [1]  68  82  63 213
#  In tutto sono 213 dati

Facciamo un po' di ripasso dei comandi visti finora, e qualche aggiunta:

# Lo stem-and-leaf
stem(T)
#  The decimal point is 1 digit(s) to the left of the |
#   99 | 69
#  100 | 289
#  101 | 36
#  102 | 012233566778999
#  103 | 0033444555566777889999
#  104 | 0000112222333333444444556666666777788888899999
#  105 | 000001111222222233333333444455556677777888899999999
#  106 | 0000011112223334444556667777899
#  107 | 000001111122223456788888899
#  108 | 000123389
#  109 | 0008
#  110 | 5
# I box-plot, tutti in un'unica finestra
dev.off(dev.list())
nomi <- c("A","B","C","T")
boxplot(A,B,C,T, horizontal=TRUE, range=0, names=nomi)
# e alcuni percentili (n indica la "ordinata")
p <- function(X,n) {points(quantile(X,0.1), n, pch=20)
                    points(quantile(X,0.9), n, pch=20)}
p(A,1); p(B,2); p(C,3); p(T,4)
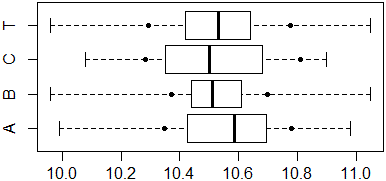
summary(T)
#   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
#   9.96   10.42   10.53   10.53   10.64   11.05
# Ho messo in fine il "sommario"

Ho usato anche il comando function che indica una funzione, ovvero qualcosa che ad input (di qualsiasi genere) associa, univocamente, output (di qualsiasi genere). In questo caso ho definito p funzione di X (che nel nostro caso è una sequenza di dati) e di n (nel nostro caso la posizione nella finestra).
Vediamo, per chiudere questa parentesi, l'istogramma:

# apro una nuova finestra
dev.new(); hist(T, col="yellow")
abline(h=axTicks(2),lty=3)
#

B - Il teorema limite centrale.   A questo punto dobbiamo affrontare il risultato più importante per le applicazioni della statistica alle scienze fisiche. Avviciniamoci ad esso sperimentalmente.

• Quasi tutti i linguaggi di programmazione e le applicazioni matematiche sono dotate di un "fenomeno casuale":

# Osserva che cosa ottieni:
runif(5)
runif(5)
dev.off(dev.list())
x <- runif(500); y <- runif(500); plot (x,y)
# Proviamo con più uscite:
dev.new(xpos=300)
x <- runif(50000); y <- runif(50000); plot (x,y, pch=".")
# Come posso descrivere la disposizione dei punti?

Senza entrare nei dettagli, diciamo che runif genera numeri (apparentemente) a caso tra 0 ed 1 con distribuzione uniforme e con ogni uscita indipendente dalle precedenti. Può esssere utilizzato, ad esempio, per simulare un dado equo, ossia tale che ogni faccia abbia la stessa probabilità di uscita delle altre, usando la funzione "parte intera" (floor).

# Vediamo ad esempio la simulazione del lancio di due dadi equi:
n <- 10000; U1 <- floor(runif(n)*6)+1; U2 <- floor(runif(n)*6)+1
hist(U1+U2, seq(1.5,12.5, 1))
# L'istogramma, ovviamente, tende alla forma di triangolo isoscele.

• Consideriamo, ora, la somma di n termini pari a √RND+3·RND²  dove con RND abbiamo indicato l'uscita del generatore di numeri casuali.

# Osserva che cosa ottieni (vediamo anche come allineare grafici):
dev.off(dev.list())
dev.new(width=8, height=3)
# con par posso dividere la finestra grafica in 1 riga e 3 col, con certi margini
par(mfrow=c(1,3), mar=c(3,3,2,1))  #
tot <- 2000; n <- 1; u <- NULL
for (i in 1:tot) { u[i] <- 0; for (j in 1:n) u[i] <- u[i]+sqrt(runif(1))+3*runif(1)^2 }
hist(u,probability=TRUE,col="yellow",main="n=1"); abline(h=axTicks(2), lty=3)
n <- 2; u <- NULL
for (i in 1:tot) { u[i] <- 0; for (j in 1:n) u[i] <- u[i]+sqrt(runif(1))+3*runif(1)^2 }
hist(u,probability=TRUE,col="yellow",main="n=2"); abline(h=axTicks(2), lty=3)
n <- 20; u <- NULL
for (i in 1:tot) { u[i] <- 0; for (j in 1:n) u[i] <- u[i]+sqrt(runif(1))+3*runif(1)^2 }
hist(u,probability=TRUE,col="yellow",main="n=20"); abline(h=axTicks(2), lty=3)
# Abbiamo scelto n = 1, 2, 20

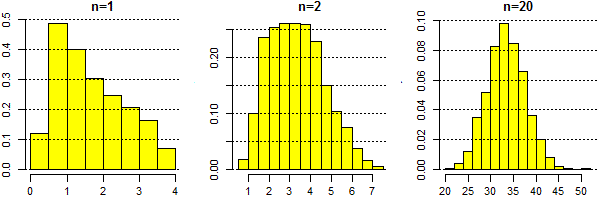
Ricordo come tutto ciò può essere precisato col teorema limite centrale:

Rivediamo l'ultimo istogramma con sovrapposta la gaussiana con m e σ pari a quelle relative a tali dati.

#
dev.off(dev.list())
tot <- 2000; n <- 20; u <- NULL
for (i in 1:tot) { u[i] <- 0; for (j in 1:n) u[i] <- u[i]+sqrt(runif(1))+3*runif(1)^2 }
hist(u,probability=TRUE,col="yellow",main="n=20"); abline(h=axTicks(2), lty=3)
# dnorm è un'abbreviazione con cui R indica la distribuzione normale
z <- function(x) dnorm(x, mean=mean(u), sd=sd(u))
curve(z, add=TRUE, lwd=2, col="blue")
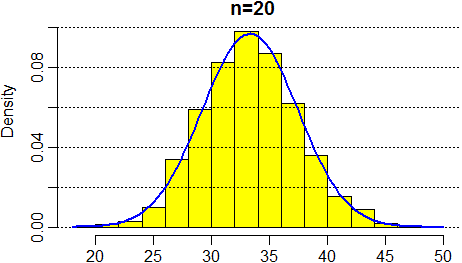
# Ho sovrapposto il grafico di z all'istogramma

• Ricordiamo le caratteristiche essenziali di ogni gaussiana, indipendenti dai valori di m e σ:

# Faccio il grafico (riducendo i margini)
dev.off(dev.list())
par( mai = c(0.4,0.4,0.15,0.1) )
# L'istogramma di 5000 valori casuali con distribuzione normale
y <- rnorm(n=5000, mean=180, sd=6)
hist(y, 20, probability=TRUE, col="yellow",lwd=2)
abline(h=axTicks(2),v=axTicks(1),col="blue",lty=3)
# La sovrapposizione della curva di distribuzione
z <- function(x) dnorm(x, mean=180, sd=6)
curve(z,add=TRUE,lwd=2,col="blue")
d <- 180+c(-6*3,-6*2,-6,6,6*2,6*3)
for(i in 1:6) lines(c(d[i],d[i]),c(0,z(d[i])), lwd=3,col="red")
# Il calcolo degli integrali tra m-σ e m+σ, m-2σ e m+2σ, m-3σ e m+3σ
integrate(z,180-6,   180+6)$value
# [1] 0.6826895
integrate(z,180-6*2, 180+6*2)$value
# [1] 0.9544997
integrate(z,180-6*3, 180+6*3)$value
# [1] 0.9973002
points(180-6,z(186),pch=19,col="green")
points(186,z(186),pch=19,col="green")
text(190,0.042,"FLESSO")
text(170,0.042,"FLESSO")
text(195,0.055,expression(sigma==6),font=2, cex=1.5)
# Ho aggiunto dei testi [con qualche sfizio: vedi]

• A questo punto abbiamo gli strumenti per capire le conclusioni fatte sull'esempio del cronometro:

• Vediamo, ad esempio, quale precisione associare alle misure del periodo del pendolo considerate sopra (se non hai più memorizzati in T i dati copia le righe da  # Ecco i dati  a  # In tutto…):

#
dev.off(dev.list())
hist(T, col="yellow", probability=TRUE)
z <- function(x) dnorm(x, mean=mean(T), sd=sd(T))
curve(z, add=TRUE, lwd=2, col="blue")
S <- sd(T)/sqrt(length(T))
lines(c(mean(T)+3*S, mean(T)+3*S),c(0,z(mean(T)+3*S)),lwd=3,lty=3)
lines(c(mean(T)-3*S, mean(T)-3*S),c(0,z(mean(T)-3*S)),lwd=3,lty=3)
c(mean(T)-3*S, mean(T)+3*S)
# Ho tracciato le rette che delimitano l'intervallo in cui al 99.7% cade la misura vera

3 - La statistica per investigare la relazione matematica tra due grandezze fisiche
A - Premessa.   Vedremo qualche flash su cose affrontabili negli ultimi anni delle superiori.

• Partiamo con un esempio, che esaminiamo a scatola nera, sui grafici delle funzioni di due variabili. In questo caso si tratta della distribuzione di (X,Y) con X e Y variabili casuali indipendenti ciascuna con andamento gaussiano, come potrebbero essere le altezze di un uomo e una donna sorteggiati a caso. Ripeto: osserviamo solo le uscite, per avere un'idea di come, con R, si possono rappresentare graficamente le funzioni di due variabili e realizzare animazioni, e si può svolgere ogni attività matematica (non solo statistica) affrontabile a scuola o nei primi anni di università. Su questo, poi, non torneremo.

# Clicca seguendo le indicazioni. Cerca di vedere il grafico da sotto il piano xy
dev.new(width=5,height=5)
f <- function(x,y) { q <- x^2+y^2; exp(-q/2)/(2*pi) }
x1 <- -5; x2 <- 5; y1 <- -5; y2 <- 5; z12 <- c(-0.02,0.18)
x <- seq(x1,x2,length=35); y <- seq(y1,y2,length=35); z <- outer(x, y, f)
teta <- -10; fi <- 15
while(TRUE) { persp(x,y,z, theta=teta,phi=fi, expand=0.5,col="yellow",shade=0.5)
  title(paste(teta,"°  ",fi,"°\nCambia vista cliccando. Finisci con ESC"))
  l <- locator(1); a <- c(l$x,l$y)
  fi <- ifelse(a[2] > 0, fi-1,fi+1); teta <- ifelse(a[1] > 0,teta-1,teta+1) }
# Quando hai finito premi ESC

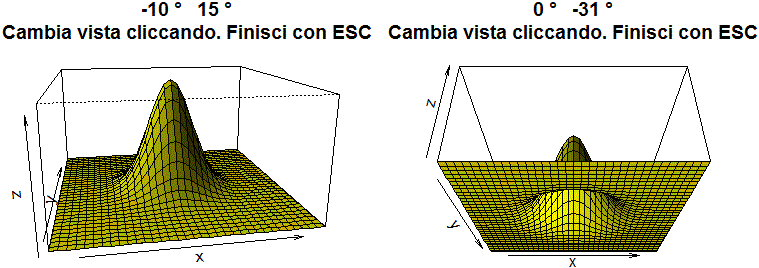
B - Come caricare e analizzare file di dati.   Abbiamo visto nel punto 2 come caricare file di singoli dati da rete.  Per vedere come recuperare altri dati e come scaricare quelli dell'Istat rinviamo (senza soffermarci su di esso ora) a questo documento.  Soffermiamoci su come caricare ed elaborare una tabella di dati.

• I dati possono essere recuperati dai siti più vari e possono essere in moltissimi formati. Vediamo un esempio che richiama alcune grandezze già esaminate in precedenza. Invece che scan per caricare tabelle si usa il comando read.table (o simili).

Quanto segue in questo punto B (colorato in grigio chiaro) può essere riassunto dal paragrafo 8 di questa scheda (letto il paragrafo, chiudi la finestra che è stata aperta) e dal seguente paragrafo (fino a nota 1 esclusa; letto il paragrafo, chiudi la finestra che è stata aperta).

A questo punto abbiamo una discreta confidenza con R e possiamo leggere direttamente comandi e uscite dal file levaR. Clicchiamo.
Per eseguire i vari comandi possiamo via via copiare e incollare le parti in nero; le parti in blu sono le uscite.  I comandi significativi nuovi che compaiono sono cor per i coefficienti di correlazione lineare, e lm per le rette di regressione, il cui significato avete già discusso nell'incontro precedente, col prof. di Bella.

• Ci soffermiamo, rapidamente, su altri quattro aspetti.
• Anche nel caso di coppie di variabili (rilevate in un contesto fisico) non è detto che si sia di fronte a misurazioni ad alta sensibilità. In questi casi si deve ricorrere a strumenti più semplici rispetto a quelli messi a disposizione dal calcolo delle probabilità. Un esempio (letto il paragrafo, chiudi la finestra che è stata aperta).
• Le statistiche sono spesso usate, inconsapevolmente o consapevolmente, erroneamente: è importante mettere a fuoco questo con gli alunni. Vai qui e vai verso i due terzi del paragrafo ("Se traccio in rettangoli cartesiani uguali, …") prima di una figura come la seguente:

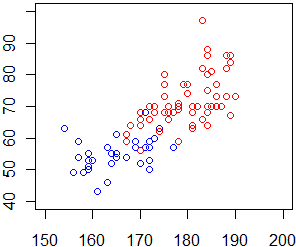
• Infine, nello stesso paragrafo qui, vedi come associare intervalli di confidenza ai coefficienti di correlazione. Non abbiamo il tempo per soffermarci su questo aspetto.

• Un ultimo argomento, importante, è quello dei test. Avete, ormai, tutti gli ingredienti per soffermarvi autonomamente su di esso. Qui potete trovare una traccia ed esempi d'uso di R (test χ², test t di Student, …), o qui.

4 - Riferimenti
Prima una osservazione su come salvare le immagini. Basta cliccare sull'immagine. Compaiono un po' di scelte. Conviene copiarla come BitMap, poi aprire Paint (o un'altra applicazione grafica) e incollarvela, spostarla, ridimensionarla per togliere il contorno inutile, eventualmente modificarla e quindi salvarla (in formato GIF o PNG od altri, per risparmiare spazio, o in formato BMP se si vuole, poi, ancora modificarla).
Qui sono indicati alcuni link che potrebbero essere utili:
 Il sito di R, per scaricarlo,
 WolframAlpha, per far di tutto,
 En.WikiPedia (solo versione inglese),
 guida ad R (guida ed esempi ad R, e link vari),
 file (e collegamenti ad Istat, Camera di Commercio, …),
 tabelle Istat (come elaborarle),
 schede di lavoro (spostati anche sulle classi precedenti e successive).