---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
# |x^2-3*x-3| < |x^2+5*x-8|
f1 = function(x) abs(x^2-3*x-3)
f2 = function(x) abs(x^2+5*x-8)
# Capisco che per x molto grande in valore assoluto le due funzioni si comportano in
# modo simile, come x^2. Vediamone comunque i grafici.
graficoF( f1, -50,50, "red"); grafico ( f2, -50,50, "seagreen")
# zommo intorno all'origine
graficoF( f1, -4,5, "red"); grafico ( f2, -4,5, "seagreen")

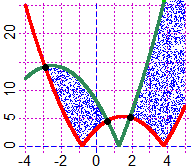 diseq(f1,f2, -4,5, "blue")
diseq(f1,f2, -4,5, "blue")
x1 = piu( soluz2(f1,f2, -4,-2) )
# [1] -2.89791576165636
x2 = piu( soluz2(f1,f2, 0,1) )
# [1] 0.625
x3 = piu( soluz2(f1,f2, 1,3) )
# [1] 1.89791576165636
PUNTO(x1,f1(x1), "black")
PUNTO(x2,f1(x2), "black")
PUNTO(x3,f1(x3), "black")
#
Posso provare a scrivere in forma esatta questi valori approssimati usando WolframAlpha.
Se metto -2.89791576165636 e poi metto 1.89791576165636 ottengo
1/2*(-1-sqrt(23)) e 1/2*(sqrt(23)-1)
Posso introdurre in WolframAlpha direttamente anche la risoluzione. Con
solve abs(x^2-3*x-3) < abs(x^2+5*x-8) for x real ottengo:
1/2*(-1-sqrt(23)) < x < 5/8 o x > 1/2*(sqrt(23)-1) OK
diseq(f1,f2, -4,5, "blue")
diseq(f1,f2, -4,5, "blue")
x1 = piu( soluz2(f1,f2, -4,-2) )
# [1] -2.89791576165636
x2 = piu( soluz2(f1,f2, 0,1) )
# [1] 0.625
x3 = piu( soluz2(f1,f2, 1,3) )
# [1] 1.89791576165636
PUNTO(x1,f1(x1), "black")
PUNTO(x2,f1(x2), "black")
PUNTO(x3,f1(x3), "black")
#
Posso provare a scrivere in forma esatta questi valori approssimati usando WolframAlpha.
Se metto -2.89791576165636 e poi metto 1.89791576165636 ottengo
1/2*(-1-sqrt(23)) e 1/2*(sqrt(23)-1)
Posso introdurre in WolframAlpha direttamente anche la risoluzione. Con
solve abs(x^2-3*x-3) < abs(x^2+5*x-8) for x real ottengo:
1/2*(-1-sqrt(23)) < x < 5/8 o x > 1/2*(sqrt(23)-1) OK

 diseq(f1,f2, -4,5, "blue")
diseq(f1,f2, -4,5, "blue")
x1 = piu( soluz2(f1,f2, -4,-2) )
# [1] -2.89791576165636
x2 = piu( soluz2(f1,f2, 0,1) )
# [1] 0.625
x3 = piu( soluz2(f1,f2, 1,3) )
# [1] 1.89791576165636
PUNTO(x1,f1(x1), "black")
PUNTO(x2,f1(x2), "black")
PUNTO(x3,f1(x3), "black")
#
Posso provare a scrivere in forma esatta questi valori approssimati usando WolframAlpha.
Se metto -2.89791576165636 e poi metto 1.89791576165636 ottengo
1/2*(-1-sqrt(23)) e 1/2*(sqrt(23)-1)
Posso introdurre in WolframAlpha direttamente anche la risoluzione. Con
solve abs(x^2-3*x-3) < abs(x^2+5*x-8) for x real ottengo:
1/2*(-1-sqrt(23)) < x < 5/8 o x > 1/2*(sqrt(23)-1) OK
diseq(f1,f2, -4,5, "blue")
diseq(f1,f2, -4,5, "blue")
x1 = piu( soluz2(f1,f2, -4,-2) )
# [1] -2.89791576165636
x2 = piu( soluz2(f1,f2, 0,1) )
# [1] 0.625
x3 = piu( soluz2(f1,f2, 1,3) )
# [1] 1.89791576165636
PUNTO(x1,f1(x1), "black")
PUNTO(x2,f1(x2), "black")
PUNTO(x3,f1(x3), "black")
#
Posso provare a scrivere in forma esatta questi valori approssimati usando WolframAlpha.
Se metto -2.89791576165636 e poi metto 1.89791576165636 ottengo
1/2*(-1-sqrt(23)) e 1/2*(sqrt(23)-1)
Posso introdurre in WolframAlpha direttamente anche la risoluzione. Con
solve abs(x^2-3*x-3) < abs(x^2+5*x-8) for x real ottengo:
1/2*(-1-sqrt(23)) < x < 5/8 o x > 1/2*(sqrt(23)-1) OK