---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
R. 2. Esempi d'uso di base (altro)
Si tratta di esempi di cose fattibili col computer. Comunque prima, eventualmente in
casi più semplici, bisogna imparare a farle "a mano".
Se vuoi, puoi vedere la versione della guida (e dei comandi) in inglese (QUI); è più
dettagliata e il linguaggio inglese usato è molto elementare, alla portata degli alunni
della scuola secondaria di 1º grado.
Clicca → QUI per un INDICE che richiama come i vari paragrafi (01, 02, …) spiegano e
illustrano come usare R per alcune attività. "Cliccando" il numero di un paragrafo
nell'indice vieni portato nel paragafo stesso. In fondo c'è un elenco alfabetico dei
vari comandi con l'indicazione del paragrafo in cui sono spiegati. In "grassetto" sono
indicati alcuni dei comandi più usati.
# (01) Nel programma i comandi appaiono preceduti da >.
# Le righe seguenti, scritte in nero (con eventuali parti in rosso), possono man mano
# essere copiate da qui e incollate in R. Il programma automaticamente le esegue.
# Le cose scritte in blu sono le uscite od altri commenti.
# Le parti che seguono # (come queste) sono per chi legge: non sono eseguite da R.
# I grafici, come quelli qui riprodotti, in R appaiono in altre finestre.
# Come spiegato nel punto (04) il "minuscolo/maiuscolo" dei comandi va rispettato.
# Dopo che hai avviato R copiaci la riga seguente:
source("http://macosa.dima.unige.it/r.R")
# Primo esempio:
5/7
# [1] 0.7142857
#
# [1] serve per numerare le righe delle uscite. In questi esempi le uscite stanno su
# una sola riga, ma se un'uscita fosse su più righe la riga seconda, la terza, …
# sarebbero precedute da [2], [3], …
#
# (02) Si possono eseguire più comandi, separati da un "punto e virgola", ossia da
# un ;. Si ottengono, uno sotto l'altro, i risultati.
5-7; 50*7; 50/7; 1+2+50
# [1] -2
# [1] 350
# [1] 7.142857
# [1] 53
# La parte frazionaria e la parte intera di un numero vengono separate da ".", non da
# ",". Così si fa in quasi tutto il mondo (e in genere si fa in "matematica", anche
# in Italia). La moltiplicazione viene indicata col simbolo *.
#
17000*100; 17000*1000
[1] 1700000
[1] 1.7e+07
# (03) Numeri lunghi, come il risultato 14000000 (6 "zero") di 14000*1000 non vengono
# scritti per esteso ma in "notazione esponenziale": la scrittura 1.4e+07 indica il
# numero 1.4*10^7 (10^7: 10 alla 7, ciò che si ottiene a partire da 1 moltiplicando
# 7 volte per 10).
#
3^2; 2^3; 5^2
# [1] 9
# [1] 8
# [1] 25
# Il simbolo "^" indica l'elevamento a potenza; quindi 2^3 e 5^2 stanno per 2 alla
# terza e 5 al quadrato.
#
# Un altro esempio di uso della notazione esponenziale:
1/1000; 1/10000
# [1] 0.001
# [1] 1e-04
# 1/10000 equivale a 1/10^4, che viene scritto anche 10^-4 (10^-4: 10 alla -4, ciò
# che si ottiene a partire da 1 dividendo 4 volte per 10).
#
# Si possono calcolare termini qualunque, rispettando le priorità tra
# le operazioni
2+3*5; (2+3)*5; 3*8/2^2; 3*(8/2)^2
# [1] 17
# [1] 25
# [1] 6
# [1] 48
# sqrt(…) calcola la radice quadrata ("square root" in inglese) di un numero
sqrt(100); sqrt(200); sqrt(200)*sqrt(200)
# [1] 10
# [1] 14.14214
# [1] 200
# Albero(1),…,Albero(17) consentono di confrontare come scrivere espressioni matemati-
# che sul computer su una solo riga, come scriverle normalmente e come rappresentarle
# con un "grafo ad albero", senza l'uso di parentesi. Saper passare tra una rappresen-
# tazione e l'altra è importante per capire il significato delle formule.
Alberi()
#Batti Albero(1) o Albero(2) ... o Albero(17): ti appaiono espressioni
#sia scritte ad "un piano", sia nel modo usuale, sia come "grafo ad albero"
Albero(8)
 # (04) Per assegnare un valore ad un "nome", cioè ad una variabile, in R si può usare
# una freccia, ossia <- o ->, o =. Nel caso di "=" la variabile va messa a sinistra.
# Per vedere il valore di una variabile occorre batterne il nome.
Prezzo <- 9; 7 -> Costo; Utile = Prezzo - Costo; Utile
# [1] 2
#
# Le dimensioni delle lettere vanno rispettate: Prezzo è una cosa diversa da PREZZO:
Prezzo; PREZZO
# [1] 9
# Errore: oggetto "PREZZO" non trovato
#
# Vediamo come potrei calcolare il 15%, ossia 15/100, di 380, 275, 637
# (il simbolo "%" sta per "/100")
p <- 15/100; p*380; p*275; p*637
# [1] 57
# [1] 41.25
# [1] 95.55
#
# (05) Una collezione di numeri può essere scritta così:
x <- c(380,275,637); x # al poso di x potevo usare qualunque altro nome
# [1] 380 275 637
# Un elemento della collezione lo ottengo mettendo il posto tra [ e ]
x[2]
# [1] 275
# Se voglio eseguire una operazione su di essi, posso comandare l'operazione
# sulla variabile che li rappresenta tutti:
x*2; (x+10)/2
# [1] 760 550 1274
# [1] 195.0 142.5 323.5
# Se voglio farne la somma ("sum" in inglese) posso fare:
sum(x)
# [1] 1292
# L'uso di c è utile quando devo usare collezioni di numeri di quantità variabile. Ad
# esempio se ai 3 dati messi in x sopra voglio aggiungere 450 e 550 faccio:
x = c(x, 450, 550); sum(x) # sum somma una qualunque quantità di numeri
# [1] 2292
# Per verificare se x è in una collezione Z posso usare il comando isin(x,Z) [che cos'è?
# isin=function(x,m) {n=length(m); v=FALSE; for(i in 1:n) if(x==m[i]) v=TRUE; v} vedi
# qui per "for" ]:
dati = c(118, 135, 127, 119, 121, 124, 130, 132, 128, 122, 121, 123, 127)
isin(135,dati); isin(120,dati); isin("D",c("A","D",3))
# [1] TRUE [1] FALSE [1] TRUE
#
# (06) Schiacciando il tasto freccia in "su" [^] si rivedono i precedenti comandi,
# con quello "giù" [v] i seguenti: cosa COMODA per rivederli, riusarli o modificarli.
# Prova ad usarli.
#
# In matematica vengono chiamate funzioni dei procedimenti per assegnare a degli input
# degli ouput: ad un numero il suo doppio, ad una coppia di numeri la loro somma, ad
# un elenco di nomi il loro elenco in ordine alfabetico, … Ecco come definirle in R.
#
# Un esempio semplice: la media di tre dati; vediamo come definire la funzione "media"
# in questo caso e 2 esempi d'uso: (3+5+10)/3 = 18/3 = 6, (-7+7+1) = 1/3 = 3.333…
# (qui uso "<-" ma, come detto, potevo usare "=")
media <- function(x,y,z) (x+y+z)/3
media(3,5,10); media(-7,7,1)
# [1] 6
# [1] 0.3333333
#
# Ecco come calcolare il costo di parmigiano reggiano dal prezzo di 19 euro al
# chilogrammo. Vediamo il costo di 2 kg, 317 g (1 g = 1 kg/1000) e di 3/4 kg:
costo <- function(kg) kg*19
costo(2); costo(317/1000); costo(3/4)
# [1] 38
# [1] 6.023 (che arrotonderò a 6 euro e 2 centesimi)
# [1] 14.25
#
# (07) Se voglio arrotondare i dati posso usare il comando round. Ecco come arrotonda-
# re il costo di 6 etti e 17 grammi (617 g) del parmigiano considerato in (06):
costo(617/1000)
# [1] 11.723
round(costo(617/1000),2) # arrotondamento a 2 posti dopo il punto (centesimi)
# [1] 11.72
round(costo(617/1000),0) # arrotondamento agli interi
# [1] 12
round(costo(617/1000),-1) # arrotondamento 1 posto prima del punto (decine)
# [1] 10
# Negli altri casi i risultati vengono visualizzati arrotondati a 7 cifre. Solo se sono
# interi vengono visualizzati esattamente, se hanno al più 12 cifre:
1.23456*7.654321; 123456*7654321
# [1] 9.449719
# [1] 944971853376
#
# (08) Ecco come scrivere semplicemente una sequenza di numeri. Tre esempi:
# la sequenza da 3 a 10 di "passo" 1; la sequenza da 3 a 10 di passo "1.5".;
# la sequenza da 3 a 10 che ha lunghezza ("length" in inglese) di 5 elementi.
seq(3,10, 1); seq(3,10, 1.5); seq(3,10, len=5)
# [1] 3 4 5 6 7 8 9 10
# [1] 3.0 4.5 6.0 7.5 9.0 # poi verrebbe 10.5 ma supera 10 e non viene scritto
# [1] 3.00 4.75 6.50 8.25 10.00
# Sequenze che variano di uno in uno possono essere introdotte con :
3:10; 3.4:-5
# [1] 3 4 5 6 7 8 9 10
# [1] 3.4 2.4 1.4 0.4 -0.6 -1.6 -2.6 -3.6 -4.6
#
# (09) frazio(7/20+1/6) [o fraction(…)] calcola 7/20+1/6 come frazione. Esempi:
frazio(0.75); frazio(1/5+3/5); frazio(1/2+1/3); frazio(120/100)
# [1] 3/4
# [1] 4/5
# [1] 5/6
# [1] 6/5
#
# Il rapporto tra due numeri posso esprimerlo in forma percentuale o, ad esempio, in
# sessantesimi:
A = 3/4; B = 36/90; A; B # i rapporti tra 3 e 4, tra 36 e 90
# [1] 0.75
# [1] 0.4
A*100; B*100 # i rapporti espressi "per cento"
# [1] 75
# [1] 40
A*60 # se A è 3/4 d'ora, sono A*60 (=45) minuti
# 45
# Per mettere in ordine dei numeri si usa sort (in inglese "sort" significa "ordinare"):
sort(c(9, 3, 5, 8/2))
# [1] 3 4 5 9
#
# div(24,9) calcola la divisione con resto di 24 per 9
# divisori(24) dà tutti i numeri interi positivi per cui è divisibile esattamente 24
# primi(24) esprime 24 come prodotto di numeri "primi" (ossia di numeri interi maggiori
# di 1 che sono multipli solo di 1 e di sé stessi; ad esempio 6 non è primo in quanto è
# eguale a 2*3): 2, 2, 2 e 3 sono i numeri primi il cui prodotto 2*2*2*3 è 24
div(13,5); divisori(750); primi(750)
# [1] 2 3
# [1] 1 2 3 5 6 10 15 25 30 50 75 125 150 250 375 750
# [1] 2 3 5 5 5
#
# MCD(…) e MCM(…) danno massimo comune divisore e minimo comune multiplo
numeri <- c(10, 6, 4); MCD(numeri); MCM(numeri)
# [1] 2
# [1] 60
#
# (10) PIANO(0,10,0,10) visualizza un parte di piano per rappresentare i punti (x,y)
# con x tra 0 e 10 ed y tra 1 e 10. La rappresentazione è fatta in modo che la varia-
# zione di una unità sull'asse x e sull'asse y corrispondano a tratti lunghi uguali.
# (quando non si traccia un grafico che rappresenta un particolare fenomeno
# i punti vengono spesso indicati usando la coppia di lettere x ed y)
PIANO(-1,5, 0,6)
# (04) Per assegnare un valore ad un "nome", cioè ad una variabile, in R si può usare
# una freccia, ossia <- o ->, o =. Nel caso di "=" la variabile va messa a sinistra.
# Per vedere il valore di una variabile occorre batterne il nome.
Prezzo <- 9; 7 -> Costo; Utile = Prezzo - Costo; Utile
# [1] 2
#
# Le dimensioni delle lettere vanno rispettate: Prezzo è una cosa diversa da PREZZO:
Prezzo; PREZZO
# [1] 9
# Errore: oggetto "PREZZO" non trovato
#
# Vediamo come potrei calcolare il 15%, ossia 15/100, di 380, 275, 637
# (il simbolo "%" sta per "/100")
p <- 15/100; p*380; p*275; p*637
# [1] 57
# [1] 41.25
# [1] 95.55
#
# (05) Una collezione di numeri può essere scritta così:
x <- c(380,275,637); x # al poso di x potevo usare qualunque altro nome
# [1] 380 275 637
# Un elemento della collezione lo ottengo mettendo il posto tra [ e ]
x[2]
# [1] 275
# Se voglio eseguire una operazione su di essi, posso comandare l'operazione
# sulla variabile che li rappresenta tutti:
x*2; (x+10)/2
# [1] 760 550 1274
# [1] 195.0 142.5 323.5
# Se voglio farne la somma ("sum" in inglese) posso fare:
sum(x)
# [1] 1292
# L'uso di c è utile quando devo usare collezioni di numeri di quantità variabile. Ad
# esempio se ai 3 dati messi in x sopra voglio aggiungere 450 e 550 faccio:
x = c(x, 450, 550); sum(x) # sum somma una qualunque quantità di numeri
# [1] 2292
# Per verificare se x è in una collezione Z posso usare il comando isin(x,Z) [che cos'è?
# isin=function(x,m) {n=length(m); v=FALSE; for(i in 1:n) if(x==m[i]) v=TRUE; v} vedi
# qui per "for" ]:
dati = c(118, 135, 127, 119, 121, 124, 130, 132, 128, 122, 121, 123, 127)
isin(135,dati); isin(120,dati); isin("D",c("A","D",3))
# [1] TRUE [1] FALSE [1] TRUE
#
# (06) Schiacciando il tasto freccia in "su" [^] si rivedono i precedenti comandi,
# con quello "giù" [v] i seguenti: cosa COMODA per rivederli, riusarli o modificarli.
# Prova ad usarli.
#
# In matematica vengono chiamate funzioni dei procedimenti per assegnare a degli input
# degli ouput: ad un numero il suo doppio, ad una coppia di numeri la loro somma, ad
# un elenco di nomi il loro elenco in ordine alfabetico, … Ecco come definirle in R.
#
# Un esempio semplice: la media di tre dati; vediamo come definire la funzione "media"
# in questo caso e 2 esempi d'uso: (3+5+10)/3 = 18/3 = 6, (-7+7+1) = 1/3 = 3.333…
# (qui uso "<-" ma, come detto, potevo usare "=")
media <- function(x,y,z) (x+y+z)/3
media(3,5,10); media(-7,7,1)
# [1] 6
# [1] 0.3333333
#
# Ecco come calcolare il costo di parmigiano reggiano dal prezzo di 19 euro al
# chilogrammo. Vediamo il costo di 2 kg, 317 g (1 g = 1 kg/1000) e di 3/4 kg:
costo <- function(kg) kg*19
costo(2); costo(317/1000); costo(3/4)
# [1] 38
# [1] 6.023 (che arrotonderò a 6 euro e 2 centesimi)
# [1] 14.25
#
# (07) Se voglio arrotondare i dati posso usare il comando round. Ecco come arrotonda-
# re il costo di 6 etti e 17 grammi (617 g) del parmigiano considerato in (06):
costo(617/1000)
# [1] 11.723
round(costo(617/1000),2) # arrotondamento a 2 posti dopo il punto (centesimi)
# [1] 11.72
round(costo(617/1000),0) # arrotondamento agli interi
# [1] 12
round(costo(617/1000),-1) # arrotondamento 1 posto prima del punto (decine)
# [1] 10
# Negli altri casi i risultati vengono visualizzati arrotondati a 7 cifre. Solo se sono
# interi vengono visualizzati esattamente, se hanno al più 12 cifre:
1.23456*7.654321; 123456*7654321
# [1] 9.449719
# [1] 944971853376
#
# (08) Ecco come scrivere semplicemente una sequenza di numeri. Tre esempi:
# la sequenza da 3 a 10 di "passo" 1; la sequenza da 3 a 10 di passo "1.5".;
# la sequenza da 3 a 10 che ha lunghezza ("length" in inglese) di 5 elementi.
seq(3,10, 1); seq(3,10, 1.5); seq(3,10, len=5)
# [1] 3 4 5 6 7 8 9 10
# [1] 3.0 4.5 6.0 7.5 9.0 # poi verrebbe 10.5 ma supera 10 e non viene scritto
# [1] 3.00 4.75 6.50 8.25 10.00
# Sequenze che variano di uno in uno possono essere introdotte con :
3:10; 3.4:-5
# [1] 3 4 5 6 7 8 9 10
# [1] 3.4 2.4 1.4 0.4 -0.6 -1.6 -2.6 -3.6 -4.6
#
# (09) frazio(7/20+1/6) [o fraction(…)] calcola 7/20+1/6 come frazione. Esempi:
frazio(0.75); frazio(1/5+3/5); frazio(1/2+1/3); frazio(120/100)
# [1] 3/4
# [1] 4/5
# [1] 5/6
# [1] 6/5
#
# Il rapporto tra due numeri posso esprimerlo in forma percentuale o, ad esempio, in
# sessantesimi:
A = 3/4; B = 36/90; A; B # i rapporti tra 3 e 4, tra 36 e 90
# [1] 0.75
# [1] 0.4
A*100; B*100 # i rapporti espressi "per cento"
# [1] 75
# [1] 40
A*60 # se A è 3/4 d'ora, sono A*60 (=45) minuti
# 45
# Per mettere in ordine dei numeri si usa sort (in inglese "sort" significa "ordinare"):
sort(c(9, 3, 5, 8/2))
# [1] 3 4 5 9
#
# div(24,9) calcola la divisione con resto di 24 per 9
# divisori(24) dà tutti i numeri interi positivi per cui è divisibile esattamente 24
# primi(24) esprime 24 come prodotto di numeri "primi" (ossia di numeri interi maggiori
# di 1 che sono multipli solo di 1 e di sé stessi; ad esempio 6 non è primo in quanto è
# eguale a 2*3): 2, 2, 2 e 3 sono i numeri primi il cui prodotto 2*2*2*3 è 24
div(13,5); divisori(750); primi(750)
# [1] 2 3
# [1] 1 2 3 5 6 10 15 25 30 50 75 125 150 250 375 750
# [1] 2 3 5 5 5
#
# MCD(…) e MCM(…) danno massimo comune divisore e minimo comune multiplo
numeri <- c(10, 6, 4); MCD(numeri); MCM(numeri)
# [1] 2
# [1] 60
#
# (10) PIANO(0,10,0,10) visualizza un parte di piano per rappresentare i punti (x,y)
# con x tra 0 e 10 ed y tra 1 e 10. La rappresentazione è fatta in modo che la varia-
# zione di una unità sull'asse x e sull'asse y corrispondano a tratti lunghi uguali.
# (quando non si traccia un grafico che rappresenta un particolare fenomeno
# i punti vengono spesso indicati usando la coppia di lettere x ed y)
PIANO(-1,5, 0,6)
 # (11) La finestra grafica visualizzata è larga ed alta circa 3 dita. Se batto BF e HF
# (base e altezza - "height" in inglese - della finestra) ottengo:
BF;HF
# [1] 3
# [1] 3
# Posso cambiare le dimensioni della finestra:
BF=2.5; HF=2.5; PIANO(-1,5, 0,6)
# (11) La finestra grafica visualizzata è larga ed alta circa 3 dita. Se batto BF e HF
# (base e altezza - "height" in inglese - della finestra) ottengo:
BF;HF
# [1] 3
# [1] 3
# Posso cambiare le dimensioni della finestra:
BF=2.5; HF=2.5; PIANO(-1,5, 0,6)
 # (12) Operando col mouse sulla barra del titolo della finestra grafica (vedi sotto)
# posso spostarla. Operando su bordi od angoli di essa posso ridimensionarla. La
# "scala" delle x e delle y rimane comunque la stessa.
# (12) Operando col mouse sulla barra del titolo della finestra grafica (vedi sotto)
# posso spostarla. Operando su bordi od angoli di essa posso ridimensionarla. La
# "scala" delle x e delle y rimane comunque la stessa.
 # Per cancellare una finestra che non mi serve ne clicco il bottone rosso X .
#
# (13) Vedremo più avanti varie figure che si possono costruire. Ecco ora un esempio:
PIANO(0,4, 0,4); cerchio(2,2, 1.5, "red"); punto(2,2, "blue")
# Per cancellare una finestra che non mi serve ne clicco il bottone rosso X .
#
# (13) Vedremo più avanti varie figure che si possono costruire. Ecco ora un esempio:
PIANO(0,4, 0,4); cerchio(2,2, 1.5, "red"); punto(2,2, "blue")

 # Ho ottenuto la figura a sinistra. Ecco come ottenere quella a destra.
# Vedi fra due righe la spiegazione.
PIANO(0,10, 0,10); x <- c(1,4,8); y <- c(6,2,5)
cerchio3p(x,y, "black"); punti(x,y,"orange")
# Nel primo caso ho tracciato il cerchio di centro (2,2) e raggio 1.5 in rosso ("red");
# ho anche tracciato in blu ("blue") il punto che corrisponde al centro.
# Nel secondo caso ho tracciato il cerchio passante per 3 punti, dei quali ho messo le
# coordinate in x e in y; poi ho tracciato i punti di coordinate x ed y.
# Le figure appaiono in finestre sovrapposte. Per vedere la vecchia figura posso
# spostare la nuova finestra come scritto sopra, in (12).
# Volendo posso avere le coordinate del centro e il raggio del cerchio così tracciato:
centro3p; raggio3p
# [1] 4.5 5.5
# [1] 3.535534
# Il pallino piccolo rosso (nel centro ora calcolato) l'ho tracciato col comando Punti:
Punti(4.5, 5.5, "red") # potevo usare anche Punto
# Col comando PUNTI (o PUNTO) si tracciano pallini leggermente più grandi; con Punt o
# punt leggeremente più piccoli.
#
# (14) Con Piano(0,10,0,20) (con la sola iniziale, "P", maiuscola) le x e le y sono
# rappresentate con scale che possono essere diverse: modificando la finestra la forma
# della figura disegnata cambia. Ecco come può apparire l'ultimo cerchio.
Piano(0,10,0,20); cerchio3p(x,y, "violet")
Piano(0,15,0,10); cerchio3p(x,y, "brown")
# Ho ottenuto la figura a sinistra. Ecco come ottenere quella a destra.
# Vedi fra due righe la spiegazione.
PIANO(0,10, 0,10); x <- c(1,4,8); y <- c(6,2,5)
cerchio3p(x,y, "black"); punti(x,y,"orange")
# Nel primo caso ho tracciato il cerchio di centro (2,2) e raggio 1.5 in rosso ("red");
# ho anche tracciato in blu ("blue") il punto che corrisponde al centro.
# Nel secondo caso ho tracciato il cerchio passante per 3 punti, dei quali ho messo le
# coordinate in x e in y; poi ho tracciato i punti di coordinate x ed y.
# Le figure appaiono in finestre sovrapposte. Per vedere la vecchia figura posso
# spostare la nuova finestra come scritto sopra, in (12).
# Volendo posso avere le coordinate del centro e il raggio del cerchio così tracciato:
centro3p; raggio3p
# [1] 4.5 5.5
# [1] 3.535534
# Il pallino piccolo rosso (nel centro ora calcolato) l'ho tracciato col comando Punti:
Punti(4.5, 5.5, "red") # potevo usare anche Punto
# Col comando PUNTI (o PUNTO) si tracciano pallini leggermente più grandi; con Punt o
# punt leggeremente più piccoli.
#
# (14) Con Piano(0,10,0,20) (con la sola iniziale, "P", maiuscola) le x e le y sono
# rappresentate con scale che possono essere diverse: modificando la finestra la forma
# della figura disegnata cambia. Ecco come può apparire l'ultimo cerchio.
Piano(0,10,0,20); cerchio3p(x,y, "violet")
Piano(0,15,0,10); cerchio3p(x,y, "brown")
 # Volendo posso evidenziare le coordinate di un qualunque punto dello schermo. Battendo:
xy(2)
# e cliccando nel punto sopra evidenziato con una croce, ottengo:
# [1] 4.5 5.5
# l'arrotondamento a 2 cifre. Se voglio ad es. 3 cifre batto xy(3)
#
# I nomi dei colori sono in inglese. Eccone alcuni:
# Volendo posso evidenziare le coordinate di un qualunque punto dello schermo. Battendo:
xy(2)
# e cliccando nel punto sopra evidenziato con una croce, ottengo:
# [1] 4.5 5.5
# l'arrotondamento a 2 cifre. Se voglio ad es. 3 cifre batto xy(3)
#
# I nomi dei colori sono in inglese. Eccone alcuni:
 # 1 black 2 grey 3 white 4 brown 5 orange 6 red 7 pink
# ( nero grigio bianco marrone arancione rosso rosa )
# 8 violet 9 blue 10 cyan 11 yellow 12 green 13 seagreen
# ( viola blu ciano giallo verde verde mare )
# Puoi comunque richiamare i nomi di un po' di colori col comando Colori()
# NOTA: al posto di "black" (colore "nero") puoi usare il numero 1:
# con cerchio3p(x,y, 1) avresti ottenuto la figura in nero
#
# (15) Vediamo come tracciare alcune figure geometriche in un sistema monometrico,
# cioè in una parte di piano rappresentata con le stesse unità per i due assi, ossia
# con il comando PIANO, introdotto sopra nel punto (10).
PIANO(0,10,0,10)
cerchio(2,8, 2, "red")
punto(6,7, "blue"); punto(4,5,"blue"); retta2p(6,7, 4,5, "blue")
segm(8,7, 8,5, "black"); segm(4,3, 6,3, "black")
punto(4,0, "brown"); punto(8,3, "brown"); semiretta(4,0, 8,3, "brown")
Segm(7,1, 10,2, "orange") # Con Segm ottengo segmenti più spessi
# Con linea li avrei sottili
# Per tracciare segmenti dato il punto inziale e la direzione vedi il punto (16)
# 1 black 2 grey 3 white 4 brown 5 orange 6 red 7 pink
# ( nero grigio bianco marrone arancione rosso rosa )
# 8 violet 9 blue 10 cyan 11 yellow 12 green 13 seagreen
# ( viola blu ciano giallo verde verde mare )
# Puoi comunque richiamare i nomi di un po' di colori col comando Colori()
# NOTA: al posto di "black" (colore "nero") puoi usare il numero 1:
# con cerchio3p(x,y, 1) avresti ottenuto la figura in nero
#
# (15) Vediamo come tracciare alcune figure geometriche in un sistema monometrico,
# cioè in una parte di piano rappresentata con le stesse unità per i due assi, ossia
# con il comando PIANO, introdotto sopra nel punto (10).
PIANO(0,10,0,10)
cerchio(2,8, 2, "red")
punto(6,7, "blue"); punto(4,5,"blue"); retta2p(6,7, 4,5, "blue")
segm(8,7, 8,5, "black"); segm(4,3, 6,3, "black")
punto(4,0, "brown"); punto(8,3, "brown"); semiretta(4,0, 8,3, "brown")
Segm(7,1, 10,2, "orange") # Con Segm ottengo segmenti più spessi
# Con linea li avrei sottili
# Per tracciare segmenti dato il punto inziale e la direzione vedi il punto (16)
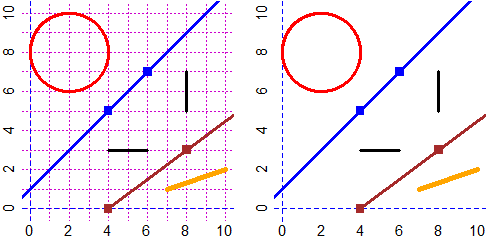 # Se uso un sistema non monometrico [vedi (14)] forme ed angoli appaiono diversi.
# Posso ottenere i grafici senza griglia, come quello sopra a destra: basta che usi
# PIANOS e PianoS invece di PIANO e Piano. Con PIANOs e Pianos non ho neanche gli
# assi. Con PIANOss e Pianoss non ho neanche la scritta delle coordinate.
# Con GRIGLIA e Griglia invece di PIANO e Piano viene rappresentata solo la griglia,
# senza l'indicazione delle coordinate. Con GRIGLIAs e Griglias non ho gli assi. Ecco
# cosa apparirebbe se, prima dei comandi precedenti, invece di PIANO(0,10, 0,10) usassi
# GRIGLIA(0,10, 0,10):
# Se uso un sistema non monometrico [vedi (14)] forme ed angoli appaiono diversi.
# Posso ottenere i grafici senza griglia, come quello sopra a destra: basta che usi
# PIANOS e PianoS invece di PIANO e Piano. Con PIANOs e Pianos non ho neanche gli
# assi. Con PIANOss e Pianoss non ho neanche la scritta delle coordinate.
# Con GRIGLIA e Griglia invece di PIANO e Piano viene rappresentata solo la griglia,
# senza l'indicazione delle coordinate. Con GRIGLIAs e Griglias non ho gli assi. Ecco
# cosa apparirebbe se, prima dei comandi precedenti, invece di PIANO(0,10, 0,10) usassi
# GRIGLIA(0,10, 0,10):
 # Il comando medio2p traccia il punto medio di 2 punti. asse2p traccia l'asse del
# segmento che ha per estremi 2 punti.
PIANO(0,10,0,10)
punto(5,1, "red"); punto(8,6, "red"); punto(8,3, "red")
medio2p(8,6, 8,3, "blue"); medio2p(5,1, 8,3, "blue") # 1ª figura
asse2p(8,6, 8,3, "brown"); asse2p(5,1, 8,3, "brown") # 2ª figura
cerchio3p(c(5,8,8), c(1,3,6), "grey")
centro3p
# [1] 4.833333 4.500000
PUNTI(4.833333,4.500000, "green") # 3ª figura
# Il comando medio2p traccia il punto medio di 2 punti. asse2p traccia l'asse del
# segmento che ha per estremi 2 punti.
PIANO(0,10,0,10)
punto(5,1, "red"); punto(8,6, "red"); punto(8,3, "red")
medio2p(8,6, 8,3, "blue"); medio2p(5,1, 8,3, "blue") # 1ª figura
asse2p(8,6, 8,3, "brown"); asse2p(5,1, 8,3, "brown") # 2ª figura
cerchio3p(c(5,8,8), c(1,3,6), "grey")
centro3p
# [1] 4.833333 4.500000
PUNTI(4.833333,4.500000, "green") # 3ª figura
 # Usando grigliaO, grigliaV, GrigliaO, GrigliaV posso tracciare griglie a piacere:
PIANOs(0,100, 0,100)
grigliaO( seq(0,100,10) ); grigliaV( seq(0,100,10) )
GrigliaO( seq(0,100,50) ); GrigliaV( seq(0,100,50) )
# Usando grigliaO, grigliaV, GrigliaO, GrigliaV posso tracciare griglie a piacere:
PIANOs(0,100, 0,100)
grigliaO( seq(0,100,10) ); grigliaV( seq(0,100,10) )
GrigliaO( seq(0,100,50) ); GrigliaV( seq(0,100,50) )
 # Con GrigliaO e GrigliaV i tratti sono più lunghi e blu scuro, con grigliaO e grigliaV
# i colori possono essere cambiati usando coltrat (vedi punto 22). Sopra a destra ciò
# che si ottiene se si è impostato coltrat="cyan4" (ciano scuro).
#
# (16) Altre figure. Alcune spezzate; la loro lunghezza; la inclinazione di una
# retta passante per 2 punti; la pendenza della retta di una data inclinazione (il
# rapporto tra l'innalzamento e l'avanzamento se si procede con quella inclinazione);
# l'inclinazione di una retta con data pendenza.
PIANO(-3,9,-2,10)
x <- c(-3,2,8,8); y <- c(1,1,9,-1)
spezzata(x,y, "green"); punti(x,y, "red")
lung(x,y)
# [1] 25
inclinazione(2,1, 8,9) # la incl. (in °) della retta per (2,1) e (8,9)
# [1] 53.1301
pendenza(53.1301) # la pendenza di una retta inclinata di 53.1301°
# [1] 1.333333
inclinazione2(11/100) # la incl. (in °) di una retta con pendenza dell'11%
# [1] 6.277298
x1 <- c(-2,2,2,-2); y1 <- c(6,6,10,10)
spezzata(x1,y1,"grey"); punti(x1,y1,"blue") # Vedi figura 1
1
# Con GrigliaO e GrigliaV i tratti sono più lunghi e blu scuro, con grigliaO e grigliaV
# i colori possono essere cambiati usando coltrat (vedi punto 22). Sopra a destra ciò
# che si ottiene se si è impostato coltrat="cyan4" (ciano scuro).
#
# (16) Altre figure. Alcune spezzate; la loro lunghezza; la inclinazione di una
# retta passante per 2 punti; la pendenza della retta di una data inclinazione (il
# rapporto tra l'innalzamento e l'avanzamento se si procede con quella inclinazione);
# l'inclinazione di una retta con data pendenza.
PIANO(-3,9,-2,10)
x <- c(-3,2,8,8); y <- c(1,1,9,-1)
spezzata(x,y, "green"); punti(x,y, "red")
lung(x,y)
# [1] 25
inclinazione(2,1, 8,9) # la incl. (in °) della retta per (2,1) e (8,9)
# [1] 53.1301
pendenza(53.1301) # la pendenza di una retta inclinata di 53.1301°
# [1] 1.333333
inclinazione2(11/100) # la incl. (in °) di una retta con pendenza dell'11%
# [1] 6.277298
x1 <- c(-2,2,2,-2); y1 <- c(6,6,10,10)
spezzata(x1,y1,"grey"); punti(x1,y1,"blue") # Vedi figura 1
1  2
2  3
3  # Poi chiudiamo ogni spezzata (spezzaC) colorandola e calcoliamo l'area del poligono
# ottenuto (vedi figura 2);
spezzaC(x,y,"yellow"); punti(x,y,"red")
spezzaC(x1,y1,"grey"); punti(x1,y1,"orange")
areaPol(x,y); areaPol(x1,y1)
# [1] 35
# [1] 16
# La figura 3 è stata costruita tracciando la spezzata con una linea sottile, mediante
# il comando spezza, e due frecce:
PIANO(-3,9,-2,10); spezza(x,y, "black"); Punti(x,y, "blue")
freccia(-2,4, 2,8, "red"); freccia(2,8, 4,6, "red")
# L'analogo comando frec traccia frecce più sottili.
# Col comando dirFreccia calcolo direzione e lunghezza di una freccia di cui siano
# dati i punti iniziale e finale:
dirFreccia(-2,4, 2,8)
# direz. = 45 ° lungh. = 5.656854
dirFreccia(2,8, 4,6)
# direz. = 315 ° lungh. = 2.828427
# Con dirFreccia1 e dirFreccia2 ho direzione (in °) e lunghezza:
dirFreccia1(-2,4, 2,8); dirFreccia2(-2,4, 2,8)
# 45 5.656854
# Con Freccia e Frec traccio le frecce dando in input direzione e lunghezza:
Freccia(-2,4, 45, 5.656854, "blue") # ho stesso esito di freccia(-2,4, 2,8, "red")
# Con Frecciax e Frecciay ho le coordinate delle punte:
Frecciax(-2,4, 45, 5.656854); Frecciay(-2,4, 45, 5.656854)
# 2 8
# Nella figura sono tracciati anche segmenti che partono da un punto x,y e proseguono
# in una direzione dir per una distanza d con Direzione(x,y, dir, d, col)
Direzione(-1,-2, 0, 5, "orange"); Direzione(-1,-2, 30, 5, "orange")
Direzione(-1,-2, 60, 5, "orange"); Direzionex; Punti(Direzionex,Direzioney, "brown")
# [1] 1.5
# Direzionex e Direzioney contengono le coordinate dei punti di arrivo. Direzio traccia
# i segmenti con linee più sottili rispetto a Direzione. Se metto il colore 0 il segm.
# non è tracciato, ma in Direzionex e Direzioney ho le coordinate dei punti di arrivo.
#
# punto_punto e punto_retta calcolano la distanza tra 2 punti e tra 1 punto e la retta
# passante per 2 punti dati.
PIANO(-3,9,-2,10)
PUNTO(2,1,"red"); PUNTO(8,9,"red"); PUNTO(8,-1,"orange")
punto_punto(2,1, 8,9)
# [1] 10
retta2p(2,1, 8,9, "blue")
punto_retta(8,-1, 2,1, 8,9)
# [1] 6
# Vedi fig. A (i due punti rossi e la retta, blu, per essi; il punto arancione)
# Poi chiudiamo ogni spezzata (spezzaC) colorandola e calcoliamo l'area del poligono
# ottenuto (vedi figura 2);
spezzaC(x,y,"yellow"); punti(x,y,"red")
spezzaC(x1,y1,"grey"); punti(x1,y1,"orange")
areaPol(x,y); areaPol(x1,y1)
# [1] 35
# [1] 16
# La figura 3 è stata costruita tracciando la spezzata con una linea sottile, mediante
# il comando spezza, e due frecce:
PIANO(-3,9,-2,10); spezza(x,y, "black"); Punti(x,y, "blue")
freccia(-2,4, 2,8, "red"); freccia(2,8, 4,6, "red")
# L'analogo comando frec traccia frecce più sottili.
# Col comando dirFreccia calcolo direzione e lunghezza di una freccia di cui siano
# dati i punti iniziale e finale:
dirFreccia(-2,4, 2,8)
# direz. = 45 ° lungh. = 5.656854
dirFreccia(2,8, 4,6)
# direz. = 315 ° lungh. = 2.828427
# Con dirFreccia1 e dirFreccia2 ho direzione (in °) e lunghezza:
dirFreccia1(-2,4, 2,8); dirFreccia2(-2,4, 2,8)
# 45 5.656854
# Con Freccia e Frec traccio le frecce dando in input direzione e lunghezza:
Freccia(-2,4, 45, 5.656854, "blue") # ho stesso esito di freccia(-2,4, 2,8, "red")
# Con Frecciax e Frecciay ho le coordinate delle punte:
Frecciax(-2,4, 45, 5.656854); Frecciay(-2,4, 45, 5.656854)
# 2 8
# Nella figura sono tracciati anche segmenti che partono da un punto x,y e proseguono
# in una direzione dir per una distanza d con Direzione(x,y, dir, d, col)
Direzione(-1,-2, 0, 5, "orange"); Direzione(-1,-2, 30, 5, "orange")
Direzione(-1,-2, 60, 5, "orange"); Direzionex; Punti(Direzionex,Direzioney, "brown")
# [1] 1.5
# Direzionex e Direzioney contengono le coordinate dei punti di arrivo. Direzio traccia
# i segmenti con linee più sottili rispetto a Direzione. Se metto il colore 0 il segm.
# non è tracciato, ma in Direzionex e Direzioney ho le coordinate dei punti di arrivo.
#
# punto_punto e punto_retta calcolano la distanza tra 2 punti e tra 1 punto e la retta
# passante per 2 punti dati.
PIANO(-3,9,-2,10)
PUNTO(2,1,"red"); PUNTO(8,9,"red"); PUNTO(8,-1,"orange")
punto_punto(2,1, 8,9)
# [1] 10
retta2p(2,1, 8,9, "blue")
punto_retta(8,-1, 2,1, 8,9)
# [1] 6
# Vedi fig. A (i due punti rossi e la retta, blu, per essi; il punto arancione)
 # retta_retta(x,y, x1,y1, p,q, p1,q1) trova l'intersezione della retta per x,y e
# x1,y1 e di quella per p,q e p1,q1. Coi comandi seguenti ottengo B: ho tracciato i
# punti verdi e la retta marrone passante per essi, e l'ho intersecata con quella blu.
PUNTO(2,-1,"green"); PUNTO(8,7,"green")
retta2p(2,-1, 8,7, "brown")
retta_retta(2,-1, 8,7, 2,1, 8,9)
# [1] "rette parallele"
# Il programma mi dice che le due rette sono parallele. Provo con un'altra retta:
# quella che va dal punto arancione al punto che indicherò col colore viola.
# Dare colori diversi alle figure mi facilita ritrovare i comandi in cui le ho usate.
PUNTO(4,10, "magenta")
retta2p(8,-1, 4,10, "grey")
retta_retta(8,-1, 4,10, 2,1, 8,9)
# [1] 5.551020 5.734694
PUNTO(5.551020, 5.734694, "black")
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta metto noStampa=1 ]
# Ho ottenuto come intersezione il pallino nero che si vede nella figura C.
# Ora provo a tracciare la perpendicolare alla retta blu che parte da 8,-1: uso il
# comando punto_retta2 (che opera come punto_retta ma invece di calcolare la distanza
# punto-retta trova le coordinate del punto di minima distanza) per trovare il punto di
# intersezione; traccio sia la semiretta che il segmento: figura D.
punto_retta2(8,-1, 2,1,8,9)
# [1] 3.2 2.6
semiretta(8,-1, 3.2,2.6, "yellow")
segm(8,-1, 3.2,2.6, "red")
PUNTO(3.2,2.6, "brown")
# Potevo procedere anche intersecando due rette descritte come "punto-direzione":
# (intersezione tra la retta blu e quella giallo-rossa)
inclinazione(2,1, 8,9)
# [1] 53.1301
retta_retta2(2,1, 53.1301, 8,-1, 53.1301+90)
# [1] 3.2 2.6
# retta_retta2(x,y, d1, p,q, d2) trova l'intersezione della retta per x,y e direzione
# d1 e di quella per p,q e direzione d2
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta2 metto noStampa=1 ]
# Per tracciare una retta, oltre al comando retta2p (che traccia la retta per due punti)
# posso usare il comando punto_inclina(x,y, dir, col) che traccia la retta per x,y
# inclinata nella direzione dir; punto_incl la traccia sottile. Esempi:
PIANO(-1,9, -2,8); PUNTO(5,4, "black")
punto_inclina(5,4, 45, "brown"); punto_inclina(5,4, 90, "red")
punto_incl(5,4, 150, "black"); punto_incl(5,4, 0, "magenta")
PUNTO(5,4, "black")
# retta_retta(x,y, x1,y1, p,q, p1,q1) trova l'intersezione della retta per x,y e
# x1,y1 e di quella per p,q e p1,q1. Coi comandi seguenti ottengo B: ho tracciato i
# punti verdi e la retta marrone passante per essi, e l'ho intersecata con quella blu.
PUNTO(2,-1,"green"); PUNTO(8,7,"green")
retta2p(2,-1, 8,7, "brown")
retta_retta(2,-1, 8,7, 2,1, 8,9)
# [1] "rette parallele"
# Il programma mi dice che le due rette sono parallele. Provo con un'altra retta:
# quella che va dal punto arancione al punto che indicherò col colore viola.
# Dare colori diversi alle figure mi facilita ritrovare i comandi in cui le ho usate.
PUNTO(4,10, "magenta")
retta2p(8,-1, 4,10, "grey")
retta_retta(8,-1, 4,10, 2,1, 8,9)
# [1] 5.551020 5.734694
PUNTO(5.551020, 5.734694, "black")
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta metto noStampa=1 ]
# Ho ottenuto come intersezione il pallino nero che si vede nella figura C.
# Ora provo a tracciare la perpendicolare alla retta blu che parte da 8,-1: uso il
# comando punto_retta2 (che opera come punto_retta ma invece di calcolare la distanza
# punto-retta trova le coordinate del punto di minima distanza) per trovare il punto di
# intersezione; traccio sia la semiretta che il segmento: figura D.
punto_retta2(8,-1, 2,1,8,9)
# [1] 3.2 2.6
semiretta(8,-1, 3.2,2.6, "yellow")
segm(8,-1, 3.2,2.6, "red")
PUNTO(3.2,2.6, "brown")
# Potevo procedere anche intersecando due rette descritte come "punto-direzione":
# (intersezione tra la retta blu e quella giallo-rossa)
inclinazione(2,1, 8,9)
# [1] 53.1301
retta_retta2(2,1, 53.1301, 8,-1, 53.1301+90)
# [1] 3.2 2.6
# retta_retta2(x,y, d1, p,q, d2) trova l'intersezione della retta per x,y e direzione
# d1 e di quella per p,q e direzione d2
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta2 metto noStampa=1 ]
# Per tracciare una retta, oltre al comando retta2p (che traccia la retta per due punti)
# posso usare il comando punto_inclina(x,y, dir, col) che traccia la retta per x,y
# inclinata nella direzione dir; punto_incl la traccia sottile. Esempi:
PIANO(-1,9, -2,8); PUNTO(5,4, "black")
punto_inclina(5,4, 45, "brown"); punto_inclina(5,4, 90, "red")
punto_incl(5,4, 150, "black"); punto_incl(5,4, 0, "magenta")
PUNTO(5,4, "black")
 # cerchio_cerchio(x1,y1,r1, x2,y2,r2) trova le eventuali intersezioni tra il cerchio
# di centro x1,y1 e raggio r1 e quello di centro x2,y2 e raggio r2. Esempi:
# cerchio_cerchio(x1,y1,r1, x2,y2,r2) trova le eventuali intersezioni tra il cerchio
# di centro x1,y1 e raggio r1 e quello di centro x2,y2 e raggio r2. Esempi:
 PIANO(-4,7,-3,8)
cerchio(0,4, 3,"brown")
cerchio(0,-1, 2,"red"); cerchio_cerchio(0,4,3, 0,-1,2)
# [1] 0 1
cerchio(4,-1, 1.5,"seagreen"); cerchio_cerchio(0,4,3, 4,-1,1.5)
# [1] "troppo distanti"
cerchio(4,6, 2,"blue"); cerchio_cerchio(0,4,3, 4,6,2)
# [1] 2.012660 6.224679 2.987340 4.275321
P=cerchio_cerchio(0,4,3, 4,6,2); PUNTO(P[1],P[2], "orange")
#
# Ecco come tracciare un poligono regolare di un certo numero N di lati con centro in
# C1,C2 inscritto nel cerchio di raggio R e un vertice con direzione G gradi:
# poligono(C1,C2, R, N,G, col). poligo lo traccia sottile, poligoC colora la parte
# interna invece del bordo.
BF=3; HF=3; PIANO(-1,5, -2,4)
punto(2,1, "blue"); cerchio(2,1, 3, "grey")
poligono(2,1, 3, 5,90, "red"); poligo(2,1, 2, 3,180, "brown")
poligo(4,3, 1, 4,0, "black"); poligoC(0,-1, 1, 4,45, "seagreen")
PIANO(-4,7,-3,8)
cerchio(0,4, 3,"brown")
cerchio(0,-1, 2,"red"); cerchio_cerchio(0,4,3, 0,-1,2)
# [1] 0 1
cerchio(4,-1, 1.5,"seagreen"); cerchio_cerchio(0,4,3, 4,-1,1.5)
# [1] "troppo distanti"
cerchio(4,6, 2,"blue"); cerchio_cerchio(0,4,3, 4,6,2)
# [1] 2.012660 6.224679 2.987340 4.275321
P=cerchio_cerchio(0,4,3, 4,6,2); PUNTO(P[1],P[2], "orange")
#
# Ecco come tracciare un poligono regolare di un certo numero N di lati con centro in
# C1,C2 inscritto nel cerchio di raggio R e un vertice con direzione G gradi:
# poligono(C1,C2, R, N,G, col). poligo lo traccia sottile, poligoC colora la parte
# interna invece del bordo.
BF=3; HF=3; PIANO(-1,5, -2,4)
punto(2,1, "blue"); cerchio(2,1, 3, "grey")
poligono(2,1, 3, 5,90, "red"); poligo(2,1, 2, 3,180, "brown")
poligo(4,3, 1, 4,0, "black"); poligoC(0,-1, 1, 4,45, "seagreen")
 #
# (17) Posso misurare le ampiezze degli angoli.
# Posso inserire scritte centrate in un punto a piacere. Un esempio.
PIANO(-1,5, -2.5,3.5)
punto(4,-2,"brown"); punto(1,1,"brown"); punto(4,3,"brown")
semiretta(1,1, 4,-2, "brown"); semiretta(1,1, 4,3,"brown")
scrivi(3.5,-2.5, "A"); scrivi(1/2,1/2, "B"); scrivi(3.5,3.5, "C")
#
# (17) Posso misurare le ampiezze degli angoli.
# Posso inserire scritte centrate in un punto a piacere. Un esempio.
PIANO(-1,5, -2.5,3.5)
punto(4,-2,"brown"); punto(1,1,"brown"); punto(4,3,"brown")
semiretta(1,1, 4,-2, "brown"); semiretta(1,1, 4,3,"brown")
scrivi(3.5,-2.5, "A"); scrivi(1/2,1/2, "B"); scrivi(3.5,3.5, "C")
 # Se voglio, come si è visto in (13), posso memorizzare i punti con un unico nome:
A=c(4,-2); B=c(1,1); C=c(4,3)
punto(A[1],A[2],"brown"); punto(B[1],B[2],"brown"); punto(C[1],C[2],"brown")
semiretta(B[1],B[2], A[1],A[2],"brown"); semiretta(B[1],B[2], C[1],C[2],"brown")
scrivi(A[1]-1/2,A[2]-1/2, "A"); scrivi(B[1]-1/2,B[2]-1/2,"B")
scrivi(C[1]-1/2,C[2]+1/2,"C")
# Misuro l'angolo ABC
angolo(A,B,C); round( angolo(A,B,C),0 )
# [1] 78.69007
# [1] 79
scrivi(2,1,"79°")
# L'angolo ABC è quello che ha vertice in B, primo lato BA e lato seguente in verso
# antiorario BC. L'angolo che va da BC a BA è indicato CBA:
angolo(C,B,A); round( angolo(C,B,A),0 )
# [1] 281.3099
# [1] 281
angolo(A,B,C)+angolo(C,B,A)
# 360
#
# Posso segnare facilmente dei punti su un cerchio dandone l'angolo che ne esprime la
# direzione in cui sono raggiungibili dal centro. Se dò il cerchio - vedi punto (13) -
# mediante centro e raggio uso i comandi cerchioA (li segno) o cerchioA2 (ne stampo le
# coordinate):
PIANO(0,4, 0,4)
cerchio(2,2, 1.5, "red")
cerchioA2(2,2, 1.5, 45)
[1] 3.06066 3.06066
cerchioA(2,2, 1.5, 45, "blue")
ang=c(90,90+45,180,180+45,270,270+45,0); cerchioA(2,2, 1.5, ang, "black")
# Vedi la figura sotto a sinistra.
# Se dò il cerchio mediante 3 punti uso i comandi cerchio3pA o cerchio3pA2:
PIANO(0,10, 0,10)
x <- c(1,4,8); y <- c(6,2,5); cerchio3p(x,y, "black")
cerchio3pA2(x,y, 90)
[1] 4.500000 9.035534
cerchio3pA(x,y, ang, "red") # vedi la figura al centro
# Se voglio, come si è visto in (13), posso memorizzare i punti con un unico nome:
A=c(4,-2); B=c(1,1); C=c(4,3)
punto(A[1],A[2],"brown"); punto(B[1],B[2],"brown"); punto(C[1],C[2],"brown")
semiretta(B[1],B[2], A[1],A[2],"brown"); semiretta(B[1],B[2], C[1],C[2],"brown")
scrivi(A[1]-1/2,A[2]-1/2, "A"); scrivi(B[1]-1/2,B[2]-1/2,"B")
scrivi(C[1]-1/2,C[2]+1/2,"C")
# Misuro l'angolo ABC
angolo(A,B,C); round( angolo(A,B,C),0 )
# [1] 78.69007
# [1] 79
scrivi(2,1,"79°")
# L'angolo ABC è quello che ha vertice in B, primo lato BA e lato seguente in verso
# antiorario BC. L'angolo che va da BC a BA è indicato CBA:
angolo(C,B,A); round( angolo(C,B,A),0 )
# [1] 281.3099
# [1] 281
angolo(A,B,C)+angolo(C,B,A)
# 360
#
# Posso segnare facilmente dei punti su un cerchio dandone l'angolo che ne esprime la
# direzione in cui sono raggiungibili dal centro. Se dò il cerchio - vedi punto (13) -
# mediante centro e raggio uso i comandi cerchioA (li segno) o cerchioA2 (ne stampo le
# coordinate):
PIANO(0,4, 0,4)
cerchio(2,2, 1.5, "red")
cerchioA2(2,2, 1.5, 45)
[1] 3.06066 3.06066
cerchioA(2,2, 1.5, 45, "blue")
ang=c(90,90+45,180,180+45,270,270+45,0); cerchioA(2,2, 1.5, ang, "black")
# Vedi la figura sotto a sinistra.
# Se dò il cerchio mediante 3 punti uso i comandi cerchio3pA o cerchio3pA2:
PIANO(0,10, 0,10)
x <- c(1,4,8); y <- c(6,2,5); cerchio3p(x,y, "black")
cerchio3pA2(x,y, 90)
[1] 4.500000 9.035534
cerchio3pA(x,y, ang, "red") # vedi la figura al centro
 # Sono comodi per individuare i punti di un cerchio anche i comandi xrot(a) e yrot(a)
# che dato un angolo a (in gradi) danno ascissa e ordinata dei punti del cerchio di
# centro 0,0 e raggio 1 raggiungibili dal centro muovendosi in direzione a.
# Sopra a destra i punti nelle direzioni 0°, 10°, 20°, 30°, ...
PIANO(-1,1, -1,1)
a=seq(0,360, 10); PUNTO( xrot(a),yrot(a), "brown" )
#
# Sappiamo che, con riga, goniometro e compasso, per costruire un triangolo mi basta
# conoscere i tre lati o due lati e l'angolo compreso o due angoli e il lato compreso.
# Qui posso costruirli usando i comandi triLLL(L1,L2,L3), triLAL(L1,A,L2) e
# triALA(A1,L,A2). Battendo LATI e ANGOLI ho le misure dei lati e degli angoli ad essi
# opposti, con TRIANGOLO() ho l'immagine del triangolo [per costruire poligoni più
# generali vedi il comando spezzata nel paragrafo precedente]
triLLL(5,5,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 5 60 60 60
triLAL(5,90,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 7.071068 45 45 90
triALA(30,8,45)
LATI; ANGOLI; TRIANGOLO()
# 5.856406 4.141105 8 45 30 105 (al lato 5.856… è opposto l'angolo di 45°, ecc.)
# Sono comodi per individuare i punti di un cerchio anche i comandi xrot(a) e yrot(a)
# che dato un angolo a (in gradi) danno ascissa e ordinata dei punti del cerchio di
# centro 0,0 e raggio 1 raggiungibili dal centro muovendosi in direzione a.
# Sopra a destra i punti nelle direzioni 0°, 10°, 20°, 30°, ...
PIANO(-1,1, -1,1)
a=seq(0,360, 10); PUNTO( xrot(a),yrot(a), "brown" )
#
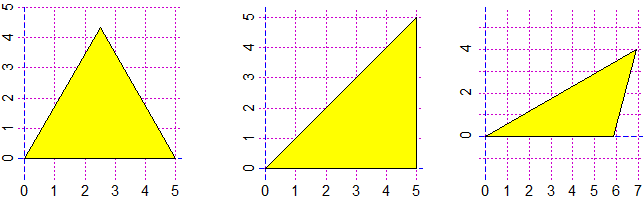
# Sappiamo che, con riga, goniometro e compasso, per costruire un triangolo mi basta
# conoscere i tre lati o due lati e l'angolo compreso o due angoli e il lato compreso.
# Qui posso costruirli usando i comandi triLLL(L1,L2,L3), triLAL(L1,A,L2) e
# triALA(A1,L,A2). Battendo LATI e ANGOLI ho le misure dei lati e degli angoli ad essi
# opposti, con TRIANGOLO() ho l'immagine del triangolo [per costruire poligoni più
# generali vedi il comando spezzata nel paragrafo precedente]
triLLL(5,5,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 5 60 60 60
triLAL(5,90,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 7.071068 45 45 90
triALA(30,8,45)
LATI; ANGOLI; TRIANGOLO()
# 5.856406 4.141105 8 45 30 105 (al lato 5.856… è opposto l'angolo di 45°, ecc.)
 #
# (18) Come realizzare il grafico di un fenomeno al variare di un altro:
# consumo medio di kg di frutta fresca all'anno consumata da un italiano.
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
# max e min - vedi il punto (20) successivo - sono utili per scegliere il "Piano"
# (qui trovo che il massimo è 88 e quindi faccio variare la y tra 0 e 90)
max(frutta)
# [1] 88
BF=4; HF=2.5
Piano(1880,1980, 0,90) # Uso "Piano" [→(14)] per avere unità diverse sui due assi
spezzata(anni,frutta, "blue"); punti(anni,frutta,"brown")
#
# (18) Come realizzare il grafico di un fenomeno al variare di un altro:
# consumo medio di kg di frutta fresca all'anno consumata da un italiano.
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
# max e min - vedi il punto (20) successivo - sono utili per scegliere il "Piano"
# (qui trovo che il massimo è 88 e quindi faccio variare la y tra 0 e 90)
max(frutta)
# [1] 88
BF=4; HF=2.5
Piano(1880,1980, 0,90) # Uso "Piano" [→(14)] per avere unità diverse sui due assi
spezzata(anni,frutta, "blue"); punti(anni,frutta,"brown")
 # Sono state messe anche delle scritte lungo gli assi con:
suassex("anni"); suassey("frutta")
#
# (19) Gli abitanti (in migliaia) del Nord, del Centro e del Mezzogiorno:
# I comandi più semplici:
N = 25755; C = 12068; S = 20843; Italia = c(N,C,S)
Barre2(Italia); torta2(Italia); Striscia2(Italia)
# % 43.90107 20.57069 35.52824
# Sono state messe anche delle scritte lungo gli assi con:
suassex("anni"); suassey("frutta")
#
# (19) Gli abitanti (in migliaia) del Nord, del Centro e del Mezzogiorno:
# I comandi più semplici:
N = 25755; C = 12068; S = 20843; Italia = c(N,C,S)
Barre2(Italia); torta2(Italia); Striscia2(Italia)
# % 43.90107 20.57069 35.52824
 HF=2; BF=2
torta(Italia) # diagramma a torta con le tacche dei centesimi
Torta(Italia) # diagramma a torta senza tacche
Tortam(Italia) # diagramma a mezza torta
HF=2; BF=2
torta(Italia) # diagramma a torta con le tacche dei centesimi
Torta(Italia) # diagramma a torta senza tacche
Tortam(Italia) # diagramma a mezza torta
 # giallo,celeste,... % 43.90107 20.57069 35.52824
# Per ottenere la distribuzione percentuale arrotondata - vedi il punto (07) - posso fare:
distribuzione(Italia, 0)
# 44 21 36
distribuzione(Italia, 2)
# 43.9 20.57 35.53 # se voglio poi scrivo 43.90 invece di 43.9
distribuzione(Italia, -1)
# 40 20 40
#
nomiBarre = c("N","C","S"); Barre(Italia)
# giallo,celeste,... % 43.90107 20.57069 35.52824
# Per ottenere la distribuzione percentuale arrotondata - vedi il punto (07) - posso fare:
distribuzione(Italia, 0)
# 44 21 36
distribuzione(Italia, 2)
# 43.9 20.57 35.53 # se voglio poi scrivo 43.90 invece di 43.9
distribuzione(Italia, -1)
# 40 20 40
#
nomiBarre = c("N","C","S"); Barre(Italia)
 # Il diagramma a destra è stato ottenuto scrivemdo prima noGriglia = 1
#
Striscia(Italia)
# Il diagramma a destra è stato ottenuto scrivemdo prima noGriglia = 1
#
Striscia(Italia)
 # Posso usare "nomi" anche per strisce e torte con nomiStriscia e nomiTorta. Es.:
nomi = c("N","C","S"); nomiTorta = nomi; torta(Italia)
giallo,celeste,... % 43.90107 20.57069 35.52824
giallo,celeste,... N C S
# Se voglio posso usare UNDER(nome,x) e ABOVE(nome,x) per mettere nomi sotto/sopra
# le barre; in x devo mettere il nome della barra. Metti 'UNDER("%",0.5)'
# se vuoi ''%' sotto l'asse y):
Bar( c(25755,12068,20843) ); ABOVE(25755,1); ABOVE(12068,2); ABOVE(20843,3)
UNDER("North",1); UNDER("Center",2); UNDER("South",3); UNDER("%",0)
# Posso usare "nomi" anche per strisce e torte con nomiStriscia e nomiTorta. Es.:
nomi = c("N","C","S"); nomiTorta = nomi; torta(Italia)
giallo,celeste,... % 43.90107 20.57069 35.52824
giallo,celeste,... N C S
# Se voglio posso usare UNDER(nome,x) e ABOVE(nome,x) per mettere nomi sotto/sopra
# le barre; in x devo mettere il nome della barra. Metti 'UNDER("%",0.5)'
# se vuoi ''%' sotto l'asse y):
Bar( c(25755,12068,20843) ); ABOVE(25755,1); ABOVE(12068,2); ABOVE(20843,3)
UNDER("North",1); UNDER("Center",2); UNDER("South",3); UNDER("%",0)
 # Posso mettere nomi sopra/sotto le strisce con above(nome,x), under(nome,x), under2(nome,x)
Striscia(c(25755,12068,20843)); above(25755,21); above(12068,53); above(20843,82)
# Posso mettere nomi sopra/sotto le strisce con above(nome,x), under(nome,x), under2(nome,x)
Striscia(c(25755,12068,20843)); above(25755,21); above(12068,53); above(20843,82)
 Striscia(c(25755,12068,20843)); above("North",21); above("Center",53); above("South",82)
under("Italy",25); under2("North-Center-South",25)
Striscia(c(25755,12068,20843)); above("North",21); above("Center",53); above("South",82)
under("Italy",25); under2("North-Center-South",25)
 #
# Una torta "vuota" ed un goniometro (il goniometro è il cerchio diviso in gradi (°),
torta(0); gonio() # cioè in 360 parti uguali).
GONIO(0) # Un quarto di goniometro
Striscia(0) # ed una striscia.
#
# Una torta "vuota" ed un goniometro (il goniometro è il cerchio diviso in gradi (°),
torta(0); gonio() # cioè in 360 parti uguali).
GONIO(0) # Un quarto di goniometro
Striscia(0) # ed una striscia.
# Volendo, nella torta e nel goniometro vuoto, puoi inserire dei raggi (lunghi 1) con
# comandi del tipo Direzione(0,0, 45,1,"blue") o Direzio(0,0, 190,1,"blue")
 |
# Con Gonio(x,y, r) posso tracciare
# un goniometro centrato in x,y
# di raggio r. Ecco a sinstra
# quello ottenuto con:
Gonio(5,6, 5)
# (centrato nel punto (5,6) e di
# raggio 5)
# Vedi qui per gli altri comandi
# che tracciano la figura.
|
Con cartamm1() ho il foglio di carta
millimetrata riproddotto a fianco
(50 mm di base e 50 mm di altezza).
Con cartamm2() e cartamm3() ho quelli
di 100 mm di base e 50 mm di altezza e
di 100 mm di base e 100 mm di altezza
(altri posso ottenerli unendo queste
immagini; per altri ancora vedi il
documento successivo)
Per aggiungere degli assi posso usare:
segm(0,-50,0,50,"black"); segm(0,-50,0,50,"black")
o ad es. segm(-50,5, 50,5, "blue") se voglio che
l'asse x sia blu e passi sopra di 5 mm | 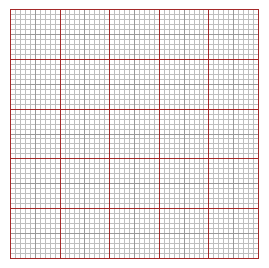 |
# Posso costruire una quadrettatura di m colonne e n righe col comando QUADRETTI(m,n)
# che la disegna in una nuova finestra:
BF=4.5; HF=1.5; QUADRETTI(15,5)
 # con BF=3; HF=3; QUADRETTI(10,10) ho quadretti con lato di circa 5 mm
# Volendo posso aprire prima uno spazio e poi aggiungere i quadretti:
PIANOss(0,15,0,5); Quadretti(15,5)
# con BF=3; HF=3; QUADRETTI(10,10) ho quadretti con lato di circa 5 mm
# Volendo posso aprire prima uno spazio e poi aggiungere i quadretti:
PIANOss(0,15,0,5); Quadretti(15,5)
# Con CROSS posso aggiungere delle crocette
QUADRETTI(5,4) # potrei accorciare i comandi
CROSS(1,1); CROSS(1,2) # usando for (vedi più avanti)
CROSS(2,1); CROSS(2,2); CROSS(2,3); CROSS(2,4)
CROSS(3,1); CROSS(3,2); CROSS(3,3)
CROSS(4,1); CROSS(4,2)
CROSS(5,1); CROSS(5,2); CROSS(5,3); CROSS(5,4)
# Con SCROSS posso aggiungere sotto delle etichette
SCROSS(1,"A"); SCROSS(2,"B"); SCROSS(3,"C")
SCROSS(4,"D"); SCROSS(5,"E")
|  |
# Posso anche realizzare facilmente dei termometri, col comando TERMOMETRO. Un esempio:
TERMOMETRO(7); TERMOMETRO(c(7,22)); TERMOMETRO2(c(3,15))# TERMOMETRO(N) realizza un termometro "vuoto" largo N (come se mettessi BF=N),
# TERMOMETRO(c(N,M)) lo realizza largo N che segna la temperatura di M gradi.
# TERMOMETRO2(N) e TERMOMETRO2(c(N,M)) operano con stampa orizzontale e più sottile, e
# sono utili per la realizzazione di testi, esercizi, …
# TERMOMETRO(N) e TERMOMETRO(c(N,M)) sono comandi utili per realizzare termometri da
# appendere in classe; ecco, rimpicciolite più volte, immagini ottenibili con N=10:
 # Altri diagrammi:
# Altri diagrammi:

 # Vedi qui. Si usano puntiO, puntiV e puntiD per tracciare i punti in varie forme.
#
# (20)
# Ecco come fare istogramma e calcoli relativi a singoli dati raccolti.
# Un esempio: le temperature alle ore 12 in un mese invernale di 31 giorni:
# (arrotondate agli interi)
T <- c(3,4,5,2,2,3,4,6,6,8,9,9,8,10,8,7,8,6,4,1,-1,3,5,7,6,9,12,11,14,13,13)
max(T);min(T)
# [1] 14
# [1] -1
# Posso controllare se i dati sono proprio 31 col comando length ("lunghezza"):
length(T)
# [1] 31
# Volendo ordinarli:
sort(T)
# [1] -1 1 2 2 3 3 3 4 4 4 5 5 6 6 6 6 7 7 8 8 8 8 9 9 9 10 11 12 13 13 14
#
isto(T)
# Vedi qui. Si usano puntiO, puntiV e puntiD per tracciare i punti in varie forme.
#
# (20)
# Ecco come fare istogramma e calcoli relativi a singoli dati raccolti.
# Un esempio: le temperature alle ore 12 in un mese invernale di 31 giorni:
# (arrotondate agli interi)
T <- c(3,4,5,2,2,3,4,6,6,8,9,9,8,10,8,7,8,6,4,1,-1,3,5,7,6,9,12,11,14,13,13)
max(T);min(T)
# [1] 14
# [1] -1
# Posso controllare se i dati sono proprio 31 col comando length ("lunghezza"):
length(T)
# [1] 31
# Volendo ordinarli:
sort(T)
# [1] -1 1 2 2 3 3 3 4 4 4 5 5 6 6 6 6 7 7 8 8 8 8 9 9 9 10 11 12 13 13 14
#
isto(T)
 # Frequenze e frequenze percentuali:
# 1, 1, 5, 5, 6, 7, 2, 4
# 3.23,3.23,16.13,16.13,19.35,22.58,6.45,12.9
# Per altre statistiche usa il comando altrestat()
# Se davanti al comando "istogramma" metto noClassi=1 invece degli estremi di
# tutte le classi appare l'intervallo complessivo e il numero delle classi
# (la cosa è comoda se le classi sono molte):
# Frequenze e frequenze percentuali:
# 1, 1, 5, 5, 6, 7, 2, 4
# 3.23,3.23,16.13,16.13,19.35,22.58,6.45,12.9
# Per altre statistiche usa il comando altrestat()
# Se davanti al comando "istogramma" metto noClassi=1 invece degli estremi di
# tutte le classi appare l'intervallo complessivo e il numero delle classi
# (la cosa è comoda se le classi sono molte):
 # A destra che cosa si ottiene se metto prima: noGriglia = 1
#
# Se invece di "isto" usi questo comando:
istogramma(T)
# compare anche:
# Per altre statistiche usa il comando altrestat()
# che elabora altre statistiche (che eventualmente studierai più avanti):
altrestat()
# A destra che cosa si ottiene se metto prima: noGriglia = 1
#
# Se invece di "isto" usi questo comando:
istogramma(T)
# compare anche:
# Per altre statistiche usa il comando altrestat()
# che elabora altre statistiche (che eventualmente studierai più avanti):
altrestat()
 # Min. 1st Qu. Median Mean 3rd Qu. Max.
# -1.000 4.000 6.000 6.613 9.000 14.000
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
# Minimo, 1° quartile (separazione tra il primo 25% dei dati e i successivi), mediana
# (o 2° quartile o 50° percentile), media, 3° quartile (o 75° percentile), massimo.
# Questo diagramma, dalla forma di una scatola ("box") con "baffi", è chiamato boxplot.
#
# Per la mediana e la media ("median" e "mean" in inglese) posso battere semplicemente
median(T); mean(T)
# [1] 6
# [1] 6.612903
# La mediana in questo caso è un numero intero in quanto i dati sono interi ed essa è
# il dato al centro dell'elenco (se sono 9 è il 5º) o immediatamente prima (se sono 8 è
# il 4º). La media invece è un numero qualunque, ottenuto facendo la somma dei dati e
# dividendola per la loro quantità. Se lanciassi molte volte un dado equo la mediana
# potrebbe essere 3 o 4, a seconda dei casi, mentre la media sarebbe vicina a 3.5.
#
# NOTA. Facendo l'istogramma i dati vengono classificati nei vari intervalli (che nell'
# esempio precedente andavano da -2 a 0, da 0 a 2, da 2 a 4, …) mettendo i numeri a
# confine tra i vari intervalli in quello a destra. Ad es. -1 viene messo tra -2 e 0
# mentre di fronte a 1,2,2 mentre 1 viene messo tra 0 e 2, 2,2 vengono messi tra 2 e 4,
# assieme a 3,3,3.
#
# Se vogliamo invece vedere il grafico delle temperature al passare dei giorni
# (che abbiamo visto variano tra -1° e 14°):
BF=5; HF=3; Piano(0,32, -2,15)
giorni = 1:31
spezzata(giorni,T, "red"); punti(giorni,T,"blue")
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# -1.000 4.000 6.000 6.613 9.000 14.000
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
# Minimo, 1° quartile (separazione tra il primo 25% dei dati e i successivi), mediana
# (o 2° quartile o 50° percentile), media, 3° quartile (o 75° percentile), massimo.
# Questo diagramma, dalla forma di una scatola ("box") con "baffi", è chiamato boxplot.
#
# Per la mediana e la media ("median" e "mean" in inglese) posso battere semplicemente
median(T); mean(T)
# [1] 6
# [1] 6.612903
# La mediana in questo caso è un numero intero in quanto i dati sono interi ed essa è
# il dato al centro dell'elenco (se sono 9 è il 5º) o immediatamente prima (se sono 8 è
# il 4º). La media invece è un numero qualunque, ottenuto facendo la somma dei dati e
# dividendola per la loro quantità. Se lanciassi molte volte un dado equo la mediana
# potrebbe essere 3 o 4, a seconda dei casi, mentre la media sarebbe vicina a 3.5.
#
# NOTA. Facendo l'istogramma i dati vengono classificati nei vari intervalli (che nell'
# esempio precedente andavano da -2 a 0, da 0 a 2, da 2 a 4, …) mettendo i numeri a
# confine tra i vari intervalli in quello a destra. Ad es. -1 viene messo tra -2 e 0
# mentre di fronte a 1,2,2 mentre 1 viene messo tra 0 e 2, 2,2 vengono messi tra 2 e 4,
# assieme a 3,3,3.
#
# Se vogliamo invece vedere il grafico delle temperature al passare dei giorni
# (che abbiamo visto variano tra -1° e 14°):
BF=5; HF=3; Piano(0,32, -2,15)
giorni = 1:31
spezzata(giorni,T, "red"); punti(giorni,T,"blue")
 # Ricordiamo che le misure erano arrotondate (3° indica che la temperatura esatta sta
# tra 2.5° e 3.5°: 3° è la misura arrotondata agli interi più vicina al valore esatto)
#
# Un altro esempio in cui vediamo come i comandi possono essere spezzati su più righe.
# Ecco le lunghezze di molte fave (ossia semi di fava) raccolte da una classe di
# alunni di 12 anni. Occorre copiare e incollare tutte le righe, da "fave <- c("
# alla riga finale ")".
#
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
#
istogramma(fave)
# Ricordiamo che le misure erano arrotondate (3° indica che la temperatura esatta sta
# tra 2.5° e 3.5°: 3° è la misura arrotondata agli interi più vicina al valore esatto)
#
# Un altro esempio in cui vediamo come i comandi possono essere spezzati su più righe.
# Ecco le lunghezze di molte fave (ossia semi di fava) raccolte da una classe di
# alunni di 12 anni. Occorre copiare e incollare tutte le righe, da "fave <- c("
# alla riga finale ")".
#
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
#
istogramma(fave)
 # Frequenze e frequenze percentuali:
# 2, 0, 0, 4, 24, 40, 64, 64, 38, 18, 2, 0, 4
# 0.77,0,0,1.54,9.23,15.38,24.62,24.62,14.62,6.92,0.77,0,1.54
# Per altre statistiche usa il comando altrestat()
mean(fave); median(fave)
# [1] 1.659
# [1] 1.65
altrestat()
# Frequenze e frequenze percentuali:
# 2, 0, 0, 4, 24, 40, 64, 64, 38, 18, 2, 0, 4
# 0.77,0,0,1.54,9.23,15.38,24.62,24.62,14.62,6.92,0.77,0,1.54
# Per altre statistiche usa il comando altrestat()
mean(fave); median(fave)
# [1] 1.659
# [1] 1.65
altrestat()
 #
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 1.000 1.550 1.650 1.659 1.750 2.300
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
#
# Volendo posso costruire l'istogramma scegliendo gli intervalli. Battendo:
Istogramma(fave, 1,2.4, 0.2)
# (con la I maiuscola) ho l'istogramma a partire da 1 fino a 2.4 in classi ampie 0.2
#
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 1.000 1.550 1.650 1.659 1.750 2.300
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
#
# Volendo posso costruire l'istogramma scegliendo gli intervalli. Battendo:
Istogramma(fave, 1,2.4, 0.2)
# (con la I maiuscola) ho l'istogramma a partire da 1 fino a 2.4 in classi ampie 0.2
 # Un modo comodo (realizzabile anche senza computer) di organizzare i dati è l'uso di
# una specie di istrogramma a crocette col comando stem (in inglese "gambo"). Esempio:
stem(fave)
# The decimal point is 1 digit(s) to the left of the |
# 10 | 00
# 11 |
# 12 |
# 13 | 0055
# 14 | 000000000000000000000055
# 15 | 0000000000000000000000005555555555555555
# 16 | 0000000000000000000000000000000000000000005555555555555555555555
# 17 | 0000000000000000000000000000000000000000005555555555555555555555
# 18 | 00000000000000000000000000000055555555
# 19 | 000000000000000055
# 20 | 00
# 21 |
# 22 | 55
# 23 | 00
# La prima scritta ("The decimal …") dice che il punto decimale è una cifra a sinistra
# di |, ossia che 10|00, 11|, … stanno per 1.0, 1.1, … Ecco come rappresenterei i
# primi sei dati di "fave" (1.35,1.65,1.80,1.40,1.65,1.80) sulla carta quadrettata.
# Il computer mette in ordine le cifre a destra di |, ma non è importante farlo.
# Un modo comodo (realizzabile anche senza computer) di organizzare i dati è l'uso di
# una specie di istrogramma a crocette col comando stem (in inglese "gambo"). Esempio:
stem(fave)
# The decimal point is 1 digit(s) to the left of the |
# 10 | 00
# 11 |
# 12 |
# 13 | 0055
# 14 | 000000000000000000000055
# 15 | 0000000000000000000000005555555555555555
# 16 | 0000000000000000000000000000000000000000005555555555555555555555
# 17 | 0000000000000000000000000000000000000000005555555555555555555555
# 18 | 00000000000000000000000000000055555555
# 19 | 000000000000000055
# 20 | 00
# 21 |
# 22 | 55
# 23 | 00
# La prima scritta ("The decimal …") dice che il punto decimale è una cifra a sinistra
# di |, ossia che 10|00, 11|, … stanno per 1.0, 1.1, … Ecco come rappresenterei i
# primi sei dati di "fave" (1.35,1.65,1.80,1.40,1.65,1.80) sulla carta quadrettata.
# Il computer mette in ordine le cifre a destra di |, ma non è importante farlo.
 # Il nome "gambo" (stem) deriva dal fatto che i dati così presentati hanno la forma di
# foglie disposte lungo un gambo.
# Con l'opzione "width=0" posso ottenere la lunghezza delle colonne
stem(fave,width=0)
# The decimal point is 1 digit(s) to the left of the |
# 10 | +2
# 11 |
# 12 |
# 13 | +4
# 14 | +24
# 15 | +40
# 16 | +64
# 17 | +64
# 18 | +38
# 19 | +18
# 20 | +2
# 21 |
# 22 | +2
# 23 | +2
#
# Avessi già avuto i dati già ordinati
# 1, 1, 1.3, 1.3, 1.35, 1.35, 1.4, 1.4, 1.4, 1.4, 1.4, ...
# potevo evitare di batterli tutti ad uno ad uno usando il comando rep(x,n) che replica
# il dato x n volte:
FAVE <- c(rep(1,2), rep(1.3,2), rep(1.35,2), rep(1.4,22), rep(1.45,2), rep(1.5,24),
rep(1.55,16), rep(1.6,42), rep(1.65,22), rep(1.7,42), rep(1.75,22), rep(1.8,30),
rep(1.85,8), rep(1.9,16), rep(1.95,2), rep(2,2), rep(2.25,2), rep(2.3,2))
#
# Per studiare dati interi posso usare il comando Istogramma dandogli gli intervalli
# centrati sui valori interi da considerare. Vediamo ad es. come studiare i seguenti
# esiti del lancio di un dado costruito con del cartoncino nel modo illustrato sotto
# a sinistra:
dado <- c(
5,5,4,3,3,1,6,2,5,6,2,5,3,6,5,6,3,2,1,6,1,6,6,3,5,2,1,5,2,5,5,3,6,6,4,6,6,5,6,2,
1,6,6,3,2,2,5,6,3,2,6,6,6,4,2,3,6,6,6,2,6,4,5,4,6,2,3,5,6,6,2,2,1,5,5,3,5,3,5,6,
2,1,4,3,6,6,6,4,3,4,6,6,4,5,4,4,2,2,6,4,4,6,2,5,3,6,6,3,3,2,2,6,1,4,6,5,3,3,4,1,
6,4,6,6,2,5,5,1,5,2,6,5,2,2,4,1,2,2,6,1,6,5,5,6,1,3,3,4,5,5,5,6,4,4,6,3,6,3,6,6,
4,2,6,6,6,1,4,5,6,5,6,5,5,5,6,6,2,1,6,3,6,6,5,3,5,2,2,4,6,6,5,2,5,5,6,6,5,2,6,1)
# A destra quello che (tendo conto che le uscite vanno da 1 a 6) ottengo con:
Istogramma(dado, 0.5,6.5, 1) # sotto gli esiti numerici
# Frequenze e frequenze percentuali:
# 16, 32, 25, 23, 40, 64
# 8, 16, 12.5, 11.5, 20, 32
mean(dado); median(dado) # la media non è circa 3.5, come in un dado equo
# [1] 4.155
# [1] 5
# NOTA. La differenza tra 0.5, 6.5 è 6; se mettessi 1, 6 la differenza sarebbe 5;
# avrei 5 intervalli e non classificherei correttamente i dati.
# Volendo realizzare l'istogramma col comando stem otterrei una rappresentazione di-
# spersa. Per concentrare le uscite devo mettere stem(…,scale=s) provando con s più
# piccolo di 1; per averle più sparse dovrei provare con un s maggiore di 1
stem(dado,scale=0.5)
The decimal point is at the |
1 | 0000000000000000
2 | 00000000000000000000000000000000
3 | 0000000000000000000000000
4 | 00000000000000000000000
5 | 0000000000000000000000000000000000000000
6 | 0000000000000000000000000000000000000000000000000000000000000000
#
# Per studiare dati già classificati in intervalli (col comando istoclas) vedi qui.
#
# (21)
# Il valore di π ("pi greca"), cioè l'area del cerchio di raggio# 1 e la
# lunghezza del semicerchio di raggio 1 (questo è un arrotondamento a 7 cifre):
pi
# [1] 3.141593
# Il nome "gambo" (stem) deriva dal fatto che i dati così presentati hanno la forma di
# foglie disposte lungo un gambo.
# Con l'opzione "width=0" posso ottenere la lunghezza delle colonne
stem(fave,width=0)
# The decimal point is 1 digit(s) to the left of the |
# 10 | +2
# 11 |
# 12 |
# 13 | +4
# 14 | +24
# 15 | +40
# 16 | +64
# 17 | +64
# 18 | +38
# 19 | +18
# 20 | +2
# 21 |
# 22 | +2
# 23 | +2
#
# Avessi già avuto i dati già ordinati
# 1, 1, 1.3, 1.3, 1.35, 1.35, 1.4, 1.4, 1.4, 1.4, 1.4, ...
# potevo evitare di batterli tutti ad uno ad uno usando il comando rep(x,n) che replica
# il dato x n volte:
FAVE <- c(rep(1,2), rep(1.3,2), rep(1.35,2), rep(1.4,22), rep(1.45,2), rep(1.5,24),
rep(1.55,16), rep(1.6,42), rep(1.65,22), rep(1.7,42), rep(1.75,22), rep(1.8,30),
rep(1.85,8), rep(1.9,16), rep(1.95,2), rep(2,2), rep(2.25,2), rep(2.3,2))
#
# Per studiare dati interi posso usare il comando Istogramma dandogli gli intervalli
# centrati sui valori interi da considerare. Vediamo ad es. come studiare i seguenti
# esiti del lancio di un dado costruito con del cartoncino nel modo illustrato sotto
# a sinistra:
dado <- c(
5,5,4,3,3,1,6,2,5,6,2,5,3,6,5,6,3,2,1,6,1,6,6,3,5,2,1,5,2,5,5,3,6,6,4,6,6,5,6,2,
1,6,6,3,2,2,5,6,3,2,6,6,6,4,2,3,6,6,6,2,6,4,5,4,6,2,3,5,6,6,2,2,1,5,5,3,5,3,5,6,
2,1,4,3,6,6,6,4,3,4,6,6,4,5,4,4,2,2,6,4,4,6,2,5,3,6,6,3,3,2,2,6,1,4,6,5,3,3,4,1,
6,4,6,6,2,5,5,1,5,2,6,5,2,2,4,1,2,2,6,1,6,5,5,6,1,3,3,4,5,5,5,6,4,4,6,3,6,3,6,6,
4,2,6,6,6,1,4,5,6,5,6,5,5,5,6,6,2,1,6,3,6,6,5,3,5,2,2,4,6,6,5,2,5,5,6,6,5,2,6,1)
# A destra quello che (tendo conto che le uscite vanno da 1 a 6) ottengo con:
Istogramma(dado, 0.5,6.5, 1) # sotto gli esiti numerici
# Frequenze e frequenze percentuali:
# 16, 32, 25, 23, 40, 64
# 8, 16, 12.5, 11.5, 20, 32
mean(dado); median(dado) # la media non è circa 3.5, come in un dado equo
# [1] 4.155
# [1] 5
# NOTA. La differenza tra 0.5, 6.5 è 6; se mettessi 1, 6 la differenza sarebbe 5;
# avrei 5 intervalli e non classificherei correttamente i dati.
# Volendo realizzare l'istogramma col comando stem otterrei una rappresentazione di-
# spersa. Per concentrare le uscite devo mettere stem(…,scale=s) provando con s più
# piccolo di 1; per averle più sparse dovrei provare con un s maggiore di 1
stem(dado,scale=0.5)
The decimal point is at the |
1 | 0000000000000000
2 | 00000000000000000000000000000000
3 | 0000000000000000000000000
4 | 00000000000000000000000
5 | 0000000000000000000000000000000000000000
6 | 0000000000000000000000000000000000000000000000000000000000000000
#
# Per studiare dati già classificati in intervalli (col comando istoclas) vedi qui.
#
# (21)
# Il valore di π ("pi greca"), cioè l'area del cerchio di raggio# 1 e la
# lunghezza del semicerchio di raggio 1 (questo è un arrotondamento a 7 cifre):
pi
# [1] 3.141593
 # Il quadrato che contiene questo cerchio ha area 2·2 = 4
# Se il raggio è 2, 3, … area e semicirconferenza sono π·4, π·9, … e π·2, π·3, …
#
# Posso trasformare dei dati in modo proporzionale. Ad esempio posso trasformare degli
# angoli espressi in gradi in angoli espressi in centesimi di giro. Oppure posso vedere
# che percentuale di 160 è 250, cioè che cosa diventa 160 se esprimo il totale con 100
# invece che con 250. Oppure su che ora (tra 1, 2, …, 12) è posizionata lancetta che
# segna i 20 minuti.
# Il quadrato che contiene questo cerchio ha area 2·2 = 4
# Se il raggio è 2, 3, … area e semicirconferenza sono π·4, π·9, … e π·2, π·3, …
#
# Posso trasformare dei dati in modo proporzionale. Ad esempio posso trasformare degli
# angoli espressi in gradi in angoli espressi in centesimi di giro. Oppure posso vedere
# che percentuale di 160 è 250, cioè che cosa diventa 160 se esprimo il totale con 100
# invece che con 250. Oppure su che ora (tra 1, 2, …, 12) è posizionata lancetta che
# segna i 20 minuti.

 # Basta che usi (eventualmente dopo aver ingrandito la finestra grafica ad esempio con
# BF=6; HF=4) i comandi PERCENTUALI(tot), che associa 100 ad un certo totale tot, e
# RAPPORTI(tot1, tot2), che associa tot2 ad un certo totale tot1. Le immagini prece-
# denti sono delle fotografie di quello che si ottiene con:
PERCENTUALI(360)
PERCENTUALI(250)
RAPPORTI(60, 12)
# Man mano che passa 1 secondo il pallino blu sale di 1. Se vuoi cambiare la velocità
# puoi mettere davanti ad uno dei comandi precedenti il comando ATTESA=t con ad es.
# al posto di t 2 se vuoi che passino 2 secondi, 1/5 (o 0.2) se vuoi che passi 1/5 di
# secondo. Se vuoi che avere solo l'immgine relativa ad un certo valore di tot o tot1
# basta che fai precedere uno dei comandi precedenti da INPUT(dato) o OUTPUT(dato)
# (se vuoi interrompere prima l'animazione premi ESC). Esempi:
ATTESA=1/5; PERCENTUALI(360)
INPUT=20; RAPPORTI(60,12)
OUTPUT=4; RAPPORTI(60,12)
# Dopo che ho usato RAPPORTI, impiegando rAPPORTI posso rappresentare più rapporti
# nella stessa finestra:
INPUT=50; RAPPORTI(100,60); INPUT=80; rAPPORTI(100,60); OUTPUT=20; rAPPORTI(100,60)
# Basta che usi (eventualmente dopo aver ingrandito la finestra grafica ad esempio con
# BF=6; HF=4) i comandi PERCENTUALI(tot), che associa 100 ad un certo totale tot, e
# RAPPORTI(tot1, tot2), che associa tot2 ad un certo totale tot1. Le immagini prece-
# denti sono delle fotografie di quello che si ottiene con:
PERCENTUALI(360)
PERCENTUALI(250)
RAPPORTI(60, 12)
# Man mano che passa 1 secondo il pallino blu sale di 1. Se vuoi cambiare la velocità
# puoi mettere davanti ad uno dei comandi precedenti il comando ATTESA=t con ad es.
# al posto di t 2 se vuoi che passino 2 secondi, 1/5 (o 0.2) se vuoi che passi 1/5 di
# secondo. Se vuoi che avere solo l'immgine relativa ad un certo valore di tot o tot1
# basta che fai precedere uno dei comandi precedenti da INPUT(dato) o OUTPUT(dato)
# (se vuoi interrompere prima l'animazione premi ESC). Esempi:
ATTESA=1/5; PERCENTUALI(360)
INPUT=20; RAPPORTI(60,12)
OUTPUT=4; RAPPORTI(60,12)
# Dopo che ho usato RAPPORTI, impiegando rAPPORTI posso rappresentare più rapporti
# nella stessa finestra:
INPUT=50; RAPPORTI(100,60); INPUT=80; rAPPORTI(100,60); OUTPUT=20; rAPPORTI(100,60)
 # Non è altro che l'automazione dell'uso della carta millimetrata:
# Non è altro che l'automazione dell'uso della carta millimetrata:
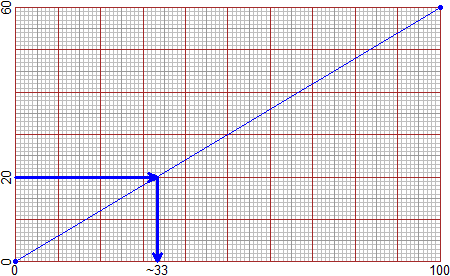 #
# (22)
# Delle funzioni numeriche ad 1 input ed 1 output possiamo fare i grafici.
#
# (22)
# Delle funzioni numeriche ad 1 input ed 1 output possiamo fare i grafici.
 # Ecco come ottenere il grafico della funzione che trasforma la temperatura in gradi
# centigradi (°C), in uso da noi, in quella in gradi Fahrenheit (°F), usati in
# Inghilterra e negli Stati Uniti.
# Uso il comando graficoF(g, a,b, col) che data una funzione g ne traccia automa-
# ticamente il grafico tra i numeri a e b nel colore col in un'opportuna Finestra.
#
Fa <- function(Ce) 32 + 72/40*Ce
graficoF(Fa, -35,105, "blue")
# Ecco come ottenere il grafico della funzione che trasforma la temperatura in gradi
# centigradi (°C), in uso da noi, in quella in gradi Fahrenheit (°F), usati in
# Inghilterra e negli Stati Uniti.
# Uso il comando graficoF(g, a,b, col) che data una funzione g ne traccia automa-
# ticamente il grafico tra i numeri a e b nel colore col in un'opportuna Finestra.
#
Fa <- function(Ce) 32 + 72/40*Ce
graficoF(Fa, -35,105, "blue")
 # Al centro che cosa si ottiene con qualche aggiunta:
scrivi(-10,225,"F")
scrivi(105,-15,"C")
segm(100,Fa(100), 0,Fa(100), 0); segm(100,Fa(100), 100,0, 0)
segm(0,Fa(0), 0,0, 0)
punto(0,Fa(0),"red"); punto(100,Fa(100),"red")
# I segmenti tratteggiati sono stati ottenuti mettendo come "colore" 0 (zero)
# Per colori diversi dei tratteggi (fig. sopra a destra) metto, ad es., coltrat="red".
#
# Se voglio mantenere la scala già scelta uso il comando grafico(g, a,b, col)
# Ecco i grafici delle funzioni x → x² e x → √x:
f1 <- function(x) x^2
f2 <- function(x) sqrt(x)
HF=3; BF=3
PIANO(-3,3,-1,5)
grafico(f1,-3,3, "brown")
grafico(f2,-3,3, "red") # tra -3 e 0 il grafico non viene tracciato
# Al centro che cosa si ottiene con qualche aggiunta:
scrivi(-10,225,"F")
scrivi(105,-15,"C")
segm(100,Fa(100), 0,Fa(100), 0); segm(100,Fa(100), 100,0, 0)
segm(0,Fa(0), 0,0, 0)
punto(0,Fa(0),"red"); punto(100,Fa(100),"red")
# I segmenti tratteggiati sono stati ottenuti mettendo come "colore" 0 (zero)
# Per colori diversi dei tratteggi (fig. sopra a destra) metto, ad es., coltrat="red".
#
# Se voglio mantenere la scala già scelta uso il comando grafico(g, a,b, col)
# Ecco i grafici delle funzioni x → x² e x → √x:
f1 <- function(x) x^2
f2 <- function(x) sqrt(x)
HF=3; BF=3
PIANO(-3,3,-1,5)
grafico(f1,-3,3, "brown")
grafico(f2,-3,3, "red") # tra -3 e 0 il grafico non viene tracciato
 # Il grafico tratteggiato è stato ottenuto mettendo come "colore" 0 (zero)
f3 <- function(x) x
grafico(f3,-3,3, 0)
#
# Il programma traccia automaticamente il grafico di una funzione per tantissimi punti.
# Posso farlo tracciare solo per un numero fissato di punti che metto in NpuntiF:
g = function(N) N*3
NpuntiF = 6; graficoF(g, 0,5, "brown")
# Il grafico tratteggiato è stato ottenuto mettendo come "colore" 0 (zero)
f3 <- function(x) x
grafico(f3,-3,3, 0)
#
# Il programma traccia automaticamente il grafico di una funzione per tantissimi punti.
# Posso farlo tracciare solo per un numero fissato di punti che metto in NpuntiF:
g = function(N) N*3
NpuntiF = 6; graficoF(g, 0,5, "brown")
 # Sopra al centro il grafico precedente sia per punti che continuo:
graficoF(g, -1,6, "yellow"); NpuntiF = 6; grafico(g, 0,5, "red")
# A destra con NPuntiF sono stati aggiunti cerchietti più grandi
NPuntiF = 6; grafico(g, 0,5, "black")
# Ecco sotto quello che ottengo usando NPUNTIF
# Sopra al centro il grafico precedente sia per punti che continuo:
graficoF(g, -1,6, "yellow"); NpuntiF = 6; grafico(g, 0,5, "red")
# A destra con NPuntiF sono stati aggiunti cerchietti più grandi
NPuntiF = 6; grafico(g, 0,5, "black")
# Ecco sotto quello che ottengo usando NPUNTIF
 NPUNTIF = 4; graficoF(g, -1,5, "blue"); NPUNTIF = 3; grafico(g, 0,4, "red")
# Oltre ai punti sono tracciati i segmenti verticali che li collegano all'asse x.
#
# Ecco come trovare i punti in cui il grafico di una funzione ha una gobba in su o in
# giù. Si usa il comando maxmin (o minmax) dando come input, oltre alla funzione,
# un intervallo che approssimi dove ciò accade:
V <- function(x) (x-1/3)^2-1
graficoF(V, -4,4, "red")
NPUNTIF = 4; graficoF(g, -1,5, "blue"); NPUNTIF = 3; grafico(g, 0,4, "red")
# Oltre ai punti sono tracciati i segmenti verticali che li collegano all'asse x.
#
# Ecco come trovare i punti in cui il grafico di una funzione ha una gobba in su o in
# giù. Si usa il comando maxmin (o minmax) dando come input, oltre alla funzione,
# un intervallo che approssimi dove ciò accade:
V <- function(x) (x-1/3)^2-1
graficoF(V, -4,4, "red")
 maxmin(V, -2,2)
# [1] 0.3333333
V( maxmin(V, -2,2) )
# [1] -1
punto(1/3,-1, "blue")
#
# Qui si può vedere come funzionano sia l'algoritmo per la ricerca dei massimi e dei
# minimi che quello per la soluzione delle equazioni.
#
# (23)
# Ecco come risolvere in modo approssimato una equazione che possiamo rappresentare
# graficamente mediante il grafico di una funzione.
# Riferiamoci all'esempio precedente e risolviamo rispetto ad x (x-1/3)^2-1 = 5, cioè
# V(x) = 5. Come sopra, basta che diamo in input, oltre alla funzione, un intervallo
# che approssimi la soluzione:
soluz(V, 5, 2,4)
# [1] 2.782823
maxmin(V, -2,2)
# [1] 0.3333333
V( maxmin(V, -2,2) )
# [1] -1
punto(1/3,-1, "blue")
#
# Qui si può vedere come funzionano sia l'algoritmo per la ricerca dei massimi e dei
# minimi che quello per la soluzione delle equazioni.
#
# (23)
# Ecco come risolvere in modo approssimato una equazione che possiamo rappresentare
# graficamente mediante il grafico di una funzione.
# Riferiamoci all'esempio precedente e risolviamo rispetto ad x (x-1/3)^2-1 = 5, cioè
# V(x) = 5. Come sopra, basta che diamo in input, oltre alla funzione, un intervallo
# che approssimi la soluzione:
soluz(V, 5, 2,4)
# [1] 2.782823
 # La soluzione è stata rappresentata graficamente con un pallino verde:
punto( 2.782823, V(2.782823), "green")
#
# In questo caso, abbastanza semplice, se si è in grado, si può risolvere l'equazione
# anche a mano:
# (x-1/3)^2-1 = 5
# porto -1 a destra cambiando segno (una sottrazione diventa una addizione):
# (x-1/3)^2 = 5+1
# faccio i calcoli:
# (x-1/3)^2 = 6
# la funzione inversa di "^2" è la radice quadrata:
# x-1/3 = √6
# porto -1/3 a destra:
# x = √6+1/3
# faccio i calcoli (con una calcolatrice o computer)
# x = 2.782823
#
# Se la soluzione dell'equazione corrisponde a un punto in cui il grafico raggiunge un
# massimo o un minimo, come nel caso seguente, per trovare la soluzione occorre usare
# il comando maxmin visto nel punto precedente.
# Soluzione dell'equazione 9*x^2-6*x = -1
# Se traccio il grafico di T con T(x) = 9*x^2-6*x (cerco x tale che T(x) = -1) ho:
# La soluzione è stata rappresentata graficamente con un pallino verde:
punto( 2.782823, V(2.782823), "green")
#
# In questo caso, abbastanza semplice, se si è in grado, si può risolvere l'equazione
# anche a mano:
# (x-1/3)^2-1 = 5
# porto -1 a destra cambiando segno (una sottrazione diventa una addizione):
# (x-1/3)^2 = 5+1
# faccio i calcoli:
# (x-1/3)^2 = 6
# la funzione inversa di "^2" è la radice quadrata:
# x-1/3 = √6
# porto -1/3 a destra:
# x = √6+1/3
# faccio i calcoli (con una calcolatrice o computer)
# x = 2.782823
#
# Se la soluzione dell'equazione corrisponde a un punto in cui il grafico raggiunge un
# massimo o un minimo, come nel caso seguente, per trovare la soluzione occorre usare
# il comando maxmin visto nel punto precedente.
# Soluzione dell'equazione 9*x^2-6*x = -1
# Se traccio il grafico di T con T(x) = 9*x^2-6*x (cerco x tale che T(x) = -1) ho:
 # Se provo a risolvere l'equazione con soluz (cerco la soluzione di T(x) = -1 tra
# -1 ed 1) ecco che cosa ottengo:
soluz(T,-1, -1,1)
# Error ... values at end points not of opposite sign
# Questo messaggio un po' strano ci dice che il grafico di T non scavalca la retta
# orizzontale y = -1. Posso trovare la soluzione cercando il minimo di T; verifico poi
# che qui T sia proprio -1.
maxmin(T, -1,1)
# [1] 0.3333333
T(1/3)
# [1] -1
# OK: la soluzione è 0.3333…, ossia 1/3.
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice:
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
# 06 Rivedere i comandi (^ v). function
# 07 Arrotondare numeri e risultati.
# 08 Le sequenze di numeri: seq :
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
punto_inclina (retta per p. con data incl.) poligono regolare poligo poligoC
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# 19 Diagrammi a torta, barre,striscia. CROSS. Goniometro. cartamm1, TERMOMETRO, …
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
# 23 Risolvere equazioni (soluz).
#
# Se provo a risolvere l'equazione con soluz (cerco la soluzione di T(x) = -1 tra
# -1 ed 1) ecco che cosa ottengo:
soluz(T,-1, -1,1)
# Error ... values at end points not of opposite sign
# Questo messaggio un po' strano ci dice che il grafico di T non scavalca la retta
# orizzontale y = -1. Posso trovare la soluzione cercando il minimo di T; verifico poi
# che qui T sia proprio -1.
maxmin(T, -1,1)
# [1] 0.3333333
T(1/3)
# [1] -1
# OK: la soluzione è 0.3333…, ossia 1/3.
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice:
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
# 06 Rivedere i comandi (^ v). function
# 07 Arrotondare numeri e risultati.
# 08 Le sequenze di numeri: seq :
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
punto_inclina (retta per p. con data incl.) poligono regolare poligo poligoC
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# 19 Diagrammi a torta, barre,striscia. CROSS. Goniometro. cartamm1, TERMOMETRO, …
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
# 23 Risolvere equazioni (soluz).
#
Comando (Numero paragrafo)
|
| ^ | 03 | |
; . * | 02 |
| : | 08 |
[^] [v] | 06 |
| […] # | 01 |
[…] | 05 |
| [X] | 12 |
= -> <- | 04 |
| Albero | 03 |
altrestat | 20 |
| angolo cerchioA cerchio3pA | 17 |
areaPol | 16 |
| asse2p | 15 |
ATTESA | 21 |
| Barre cartamm1 QUADRETTI CROSS… | 19 |
BF HF | 11 |
| c(…) isin | 05 |
cerchio cerchio3p centro3p | 13 |
| cerchio_cerchio | 16 |
Colori | 14 |
| coltrat | 22 |
Direzione Direzionex ... dirFreccia | 16 |
| distribuzione | 19 |
div divisori frazio | 09 |
| e | 03 |
freccia frec | 16 |
| function | 06 |
gonio() | 19 |
| grafico graficoF | 22 |
GRIGLIA Griglia GRIGLIAs Griglias | 15 |
| grigliaO grigliaV GrigliaO GrigliaV | 15 |
INPUT | 21 |
| istoclas | 20 |
isto(gramma) Isto(gramma) | 20 |
| length | 20 |
linea | 15 |
| lung | 16 |
max min | 20 |
| max | 18 |
maxmin minmax | 22 |
| MCD MCM | 09 |
mean median | 20 |
| medio2p | 15 |
noClassi | 20 |
| noGriglia | 19 |
NpuntiF NPuntiF NPUNTIF | 22 |
| OUTPUT | 21 |
pendenza inclinazione | 16 |
| PERCENTUALI | 21 |
pi | 21 |
| PIANO | 10 |
Piano | 14 |
| PIANOS PianoS ... PIANOss Pianoss | 15 |
poligono poligo poligoC | 16 |
| primi | 09 |
punto punti PUNTI Punti Punt | 13 |
| punto_punto punto_retta punto_inclina | 16 |
raggio3p | 13 |
| RAPPORTI | 21 |
rep | 20 |
| retta_retta retta_retta2 | 16 |
retta2p | 15 |
| round | 07 |
scrivi | 17 |
| segm Segm | 15 |
semiretta | 15 |
| seq | 08 |
soluz | 23 |
| sort | 09 |
spezzata spezza spezzaC | 16 |
| sqrt | 03 |
[statistica] | 20 |
| stem | 20 |
Striscia | 19 |
| suassex suassey | 18 |
sum | 05 |
| TERMOMETRO TERMOMETRO2 | 19 |
torta Torta Tortam torta(0) | 19 |
| [tratteggi] | 22 | triLLL triLAL triALA (triangoli) | 17 |
| xrot yrot | 17 | xy (coordinate punti cliccati) | 14 |
|
 # (04) Per assegnare un valore ad un "nome", cioè ad una variabile, in R si può usare
# una freccia, ossia <- o ->, o =. Nel caso di "=" la variabile va messa a sinistra.
# Per vedere il valore di una variabile occorre batterne il nome.
Prezzo <- 9; 7 -> Costo; Utile = Prezzo - Costo; Utile
# [1] 2
#
# Le dimensioni delle lettere vanno rispettate: Prezzo è una cosa diversa da PREZZO:
Prezzo; PREZZO
# [1] 9
# Errore: oggetto "PREZZO" non trovato
#
# Vediamo come potrei calcolare il 15%, ossia 15/100, di 380, 275, 637
# (il simbolo "%" sta per "/100")
p <- 15/100; p*380; p*275; p*637
# [1] 57
# [1] 41.25
# [1] 95.55
#
# (05) Una collezione di numeri può essere scritta così:
x <- c(380,275,637); x # al poso di x potevo usare qualunque altro nome
# [1] 380 275 637
# Un elemento della collezione lo ottengo mettendo il posto tra [ e ]
x[2]
# [1] 275
# Se voglio eseguire una operazione su di essi, posso comandare l'operazione
# sulla variabile che li rappresenta tutti:
x*2; (x+10)/2
# [1] 760 550 1274
# [1] 195.0 142.5 323.5
# Se voglio farne la somma ("sum" in inglese) posso fare:
sum(x)
# [1] 1292
# L'uso di c è utile quando devo usare collezioni di numeri di quantità variabile. Ad
# esempio se ai 3 dati messi in x sopra voglio aggiungere 450 e 550 faccio:
x = c(x, 450, 550); sum(x) # sum somma una qualunque quantità di numeri
# [1] 2292
# Per verificare se x è in una collezione Z posso usare il comando isin(x,Z) [che cos'è?
# isin=function(x,m) {n=length(m); v=FALSE; for(i in 1:n) if(x==m[i]) v=TRUE; v} vedi
# qui per "for" ]:
dati = c(118, 135, 127, 119, 121, 124, 130, 132, 128, 122, 121, 123, 127)
isin(135,dati); isin(120,dati); isin("D",c("A","D",3))
# [1] TRUE [1] FALSE [1] TRUE
#
# (06) Schiacciando il tasto freccia in "su" [^] si rivedono i precedenti comandi,
# con quello "giù" [v] i seguenti: cosa COMODA per rivederli, riusarli o modificarli.
# Prova ad usarli.
#
# In matematica vengono chiamate funzioni dei procedimenti per assegnare a degli input
# degli ouput: ad un numero il suo doppio, ad una coppia di numeri la loro somma, ad
# un elenco di nomi il loro elenco in ordine alfabetico, … Ecco come definirle in R.
#
# Un esempio semplice: la media di tre dati; vediamo come definire la funzione "media"
# in questo caso e 2 esempi d'uso: (3+5+10)/3 = 18/3 = 6, (-7+7+1) = 1/3 = 3.333…
# (qui uso "<-" ma, come detto, potevo usare "=")
media <- function(x,y,z) (x+y+z)/3
media(3,5,10); media(-7,7,1)
# [1] 6
# [1] 0.3333333
#
# Ecco come calcolare il costo di parmigiano reggiano dal prezzo di 19 euro al
# chilogrammo. Vediamo il costo di 2 kg, 317 g (1 g = 1 kg/1000) e di 3/4 kg:
costo <- function(kg) kg*19
costo(2); costo(317/1000); costo(3/4)
# [1] 38
# [1] 6.023 (che arrotonderò a 6 euro e 2 centesimi)
# [1] 14.25
#
# (07) Se voglio arrotondare i dati posso usare il comando round. Ecco come arrotonda-
# re il costo di 6 etti e 17 grammi (617 g) del parmigiano considerato in (06):
costo(617/1000)
# [1] 11.723
round(costo(617/1000),2) # arrotondamento a 2 posti dopo il punto (centesimi)
# [1] 11.72
round(costo(617/1000),0) # arrotondamento agli interi
# [1] 12
round(costo(617/1000),-1) # arrotondamento 1 posto prima del punto (decine)
# [1] 10
# Negli altri casi i risultati vengono visualizzati arrotondati a 7 cifre. Solo se sono
# interi vengono visualizzati esattamente, se hanno al più 12 cifre:
1.23456*7.654321; 123456*7654321
# [1] 9.449719
# [1] 944971853376
#
# (08) Ecco come scrivere semplicemente una sequenza di numeri. Tre esempi:
# la sequenza da 3 a 10 di "passo" 1; la sequenza da 3 a 10 di passo "1.5".;
# la sequenza da 3 a 10 che ha lunghezza ("length" in inglese) di 5 elementi.
seq(3,10, 1); seq(3,10, 1.5); seq(3,10, len=5)
# [1] 3 4 5 6 7 8 9 10
# [1] 3.0 4.5 6.0 7.5 9.0 # poi verrebbe 10.5 ma supera 10 e non viene scritto
# [1] 3.00 4.75 6.50 8.25 10.00
# Sequenze che variano di uno in uno possono essere introdotte con :
3:10; 3.4:-5
# [1] 3 4 5 6 7 8 9 10
# [1] 3.4 2.4 1.4 0.4 -0.6 -1.6 -2.6 -3.6 -4.6
#
# (09) frazio(7/20+1/6) [o fraction(…)] calcola 7/20+1/6 come frazione. Esempi:
frazio(0.75); frazio(1/5+3/5); frazio(1/2+1/3); frazio(120/100)
# [1] 3/4
# [1] 4/5
# [1] 5/6
# [1] 6/5
#
# Il rapporto tra due numeri posso esprimerlo in forma percentuale o, ad esempio, in
# sessantesimi:
A = 3/4; B = 36/90; A; B # i rapporti tra 3 e 4, tra 36 e 90
# [1] 0.75
# [1] 0.4
A*100; B*100 # i rapporti espressi "per cento"
# [1] 75
# [1] 40
A*60 # se A è 3/4 d'ora, sono A*60 (=45) minuti
# 45
# Per mettere in ordine dei numeri si usa sort (in inglese "sort" significa "ordinare"):
sort(c(9, 3, 5, 8/2))
# [1] 3 4 5 9
#
# div(24,9) calcola la divisione con resto di 24 per 9
# divisori(24) dà tutti i numeri interi positivi per cui è divisibile esattamente 24
# primi(24) esprime 24 come prodotto di numeri "primi" (ossia di numeri interi maggiori
# di 1 che sono multipli solo di 1 e di sé stessi; ad esempio 6 non è primo in quanto è
# eguale a 2*3): 2, 2, 2 e 3 sono i numeri primi il cui prodotto 2*2*2*3 è 24
div(13,5); divisori(750); primi(750)
# [1] 2 3
# [1] 1 2 3 5 6 10 15 25 30 50 75 125 150 250 375 750
# [1] 2 3 5 5 5
#
# MCD(…) e MCM(…) danno massimo comune divisore e minimo comune multiplo
numeri <- c(10, 6, 4); MCD(numeri); MCM(numeri)
# [1] 2
# [1] 60
#
# (10) PIANO(0,10,0,10) visualizza un parte di piano per rappresentare i punti (x,y)
# con x tra 0 e 10 ed y tra 1 e 10. La rappresentazione è fatta in modo che la varia-
# zione di una unità sull'asse x e sull'asse y corrispondano a tratti lunghi uguali.
# (quando non si traccia un grafico che rappresenta un particolare fenomeno
# i punti vengono spesso indicati usando la coppia di lettere x ed y)
PIANO(-1,5, 0,6)
# (04) Per assegnare un valore ad un "nome", cioè ad una variabile, in R si può usare
# una freccia, ossia <- o ->, o =. Nel caso di "=" la variabile va messa a sinistra.
# Per vedere il valore di una variabile occorre batterne il nome.
Prezzo <- 9; 7 -> Costo; Utile = Prezzo - Costo; Utile
# [1] 2
#
# Le dimensioni delle lettere vanno rispettate: Prezzo è una cosa diversa da PREZZO:
Prezzo; PREZZO
# [1] 9
# Errore: oggetto "PREZZO" non trovato
#
# Vediamo come potrei calcolare il 15%, ossia 15/100, di 380, 275, 637
# (il simbolo "%" sta per "/100")
p <- 15/100; p*380; p*275; p*637
# [1] 57
# [1] 41.25
# [1] 95.55
#
# (05) Una collezione di numeri può essere scritta così:
x <- c(380,275,637); x # al poso di x potevo usare qualunque altro nome
# [1] 380 275 637
# Un elemento della collezione lo ottengo mettendo il posto tra [ e ]
x[2]
# [1] 275
# Se voglio eseguire una operazione su di essi, posso comandare l'operazione
# sulla variabile che li rappresenta tutti:
x*2; (x+10)/2
# [1] 760 550 1274
# [1] 195.0 142.5 323.5
# Se voglio farne la somma ("sum" in inglese) posso fare:
sum(x)
# [1] 1292
# L'uso di c è utile quando devo usare collezioni di numeri di quantità variabile. Ad
# esempio se ai 3 dati messi in x sopra voglio aggiungere 450 e 550 faccio:
x = c(x, 450, 550); sum(x) # sum somma una qualunque quantità di numeri
# [1] 2292
# Per verificare se x è in una collezione Z posso usare il comando isin(x,Z) [che cos'è?
# isin=function(x,m) {n=length(m); v=FALSE; for(i in 1:n) if(x==m[i]) v=TRUE; v} vedi
# qui per "for" ]:
dati = c(118, 135, 127, 119, 121, 124, 130, 132, 128, 122, 121, 123, 127)
isin(135,dati); isin(120,dati); isin("D",c("A","D",3))
# [1] TRUE [1] FALSE [1] TRUE
#
# (06) Schiacciando il tasto freccia in "su" [^] si rivedono i precedenti comandi,
# con quello "giù" [v] i seguenti: cosa COMODA per rivederli, riusarli o modificarli.
# Prova ad usarli.
#
# In matematica vengono chiamate funzioni dei procedimenti per assegnare a degli input
# degli ouput: ad un numero il suo doppio, ad una coppia di numeri la loro somma, ad
# un elenco di nomi il loro elenco in ordine alfabetico, … Ecco come definirle in R.
#
# Un esempio semplice: la media di tre dati; vediamo come definire la funzione "media"
# in questo caso e 2 esempi d'uso: (3+5+10)/3 = 18/3 = 6, (-7+7+1) = 1/3 = 3.333…
# (qui uso "<-" ma, come detto, potevo usare "=")
media <- function(x,y,z) (x+y+z)/3
media(3,5,10); media(-7,7,1)
# [1] 6
# [1] 0.3333333
#
# Ecco come calcolare il costo di parmigiano reggiano dal prezzo di 19 euro al
# chilogrammo. Vediamo il costo di 2 kg, 317 g (1 g = 1 kg/1000) e di 3/4 kg:
costo <- function(kg) kg*19
costo(2); costo(317/1000); costo(3/4)
# [1] 38
# [1] 6.023 (che arrotonderò a 6 euro e 2 centesimi)
# [1] 14.25
#
# (07) Se voglio arrotondare i dati posso usare il comando round. Ecco come arrotonda-
# re il costo di 6 etti e 17 grammi (617 g) del parmigiano considerato in (06):
costo(617/1000)
# [1] 11.723
round(costo(617/1000),2) # arrotondamento a 2 posti dopo il punto (centesimi)
# [1] 11.72
round(costo(617/1000),0) # arrotondamento agli interi
# [1] 12
round(costo(617/1000),-1) # arrotondamento 1 posto prima del punto (decine)
# [1] 10
# Negli altri casi i risultati vengono visualizzati arrotondati a 7 cifre. Solo se sono
# interi vengono visualizzati esattamente, se hanno al più 12 cifre:
1.23456*7.654321; 123456*7654321
# [1] 9.449719
# [1] 944971853376
#
# (08) Ecco come scrivere semplicemente una sequenza di numeri. Tre esempi:
# la sequenza da 3 a 10 di "passo" 1; la sequenza da 3 a 10 di passo "1.5".;
# la sequenza da 3 a 10 che ha lunghezza ("length" in inglese) di 5 elementi.
seq(3,10, 1); seq(3,10, 1.5); seq(3,10, len=5)
# [1] 3 4 5 6 7 8 9 10
# [1] 3.0 4.5 6.0 7.5 9.0 # poi verrebbe 10.5 ma supera 10 e non viene scritto
# [1] 3.00 4.75 6.50 8.25 10.00
# Sequenze che variano di uno in uno possono essere introdotte con :
3:10; 3.4:-5
# [1] 3 4 5 6 7 8 9 10
# [1] 3.4 2.4 1.4 0.4 -0.6 -1.6 -2.6 -3.6 -4.6
#
# (09) frazio(7/20+1/6) [o fraction(…)] calcola 7/20+1/6 come frazione. Esempi:
frazio(0.75); frazio(1/5+3/5); frazio(1/2+1/3); frazio(120/100)
# [1] 3/4
# [1] 4/5
# [1] 5/6
# [1] 6/5
#
# Il rapporto tra due numeri posso esprimerlo in forma percentuale o, ad esempio, in
# sessantesimi:
A = 3/4; B = 36/90; A; B # i rapporti tra 3 e 4, tra 36 e 90
# [1] 0.75
# [1] 0.4
A*100; B*100 # i rapporti espressi "per cento"
# [1] 75
# [1] 40
A*60 # se A è 3/4 d'ora, sono A*60 (=45) minuti
# 45
# Per mettere in ordine dei numeri si usa sort (in inglese "sort" significa "ordinare"):
sort(c(9, 3, 5, 8/2))
# [1] 3 4 5 9
#
# div(24,9) calcola la divisione con resto di 24 per 9
# divisori(24) dà tutti i numeri interi positivi per cui è divisibile esattamente 24
# primi(24) esprime 24 come prodotto di numeri "primi" (ossia di numeri interi maggiori
# di 1 che sono multipli solo di 1 e di sé stessi; ad esempio 6 non è primo in quanto è
# eguale a 2*3): 2, 2, 2 e 3 sono i numeri primi il cui prodotto 2*2*2*3 è 24
div(13,5); divisori(750); primi(750)
# [1] 2 3
# [1] 1 2 3 5 6 10 15 25 30 50 75 125 150 250 375 750
# [1] 2 3 5 5 5
#
# MCD(…) e MCM(…) danno massimo comune divisore e minimo comune multiplo
numeri <- c(10, 6, 4); MCD(numeri); MCM(numeri)
# [1] 2
# [1] 60
#
# (10) PIANO(0,10,0,10) visualizza un parte di piano per rappresentare i punti (x,y)
# con x tra 0 e 10 ed y tra 1 e 10. La rappresentazione è fatta in modo che la varia-
# zione di una unità sull'asse x e sull'asse y corrispondano a tratti lunghi uguali.
# (quando non si traccia un grafico che rappresenta un particolare fenomeno
# i punti vengono spesso indicati usando la coppia di lettere x ed y)
PIANO(-1,5, 0,6)
 # (11) La finestra grafica visualizzata è larga ed alta circa 3 dita. Se batto BF e HF
# (base e altezza - "height" in inglese - della finestra) ottengo:
BF;HF
# [1] 3
# [1] 3
# Posso cambiare le dimensioni della finestra:
BF=2.5; HF=2.5; PIANO(-1,5, 0,6)
# (11) La finestra grafica visualizzata è larga ed alta circa 3 dita. Se batto BF e HF
# (base e altezza - "height" in inglese - della finestra) ottengo:
BF;HF
# [1] 3
# [1] 3
# Posso cambiare le dimensioni della finestra:
BF=2.5; HF=2.5; PIANO(-1,5, 0,6)
 # (12) Operando col mouse sulla barra del titolo della finestra grafica (vedi sotto)
# posso spostarla. Operando su bordi od angoli di essa posso ridimensionarla. La
# "scala" delle x e delle y rimane comunque la stessa.
# (12) Operando col mouse sulla barra del titolo della finestra grafica (vedi sotto)
# posso spostarla. Operando su bordi od angoli di essa posso ridimensionarla. La
# "scala" delle x e delle y rimane comunque la stessa.
 # Per cancellare una finestra che non mi serve ne clicco il bottone rosso X .
#
# (13) Vedremo più avanti varie figure che si possono costruire. Ecco ora un esempio:
PIANO(0,4, 0,4); cerchio(2,2, 1.5, "red"); punto(2,2, "blue")
# Per cancellare una finestra che non mi serve ne clicco il bottone rosso X .
#
# (13) Vedremo più avanti varie figure che si possono costruire. Ecco ora un esempio:
PIANO(0,4, 0,4); cerchio(2,2, 1.5, "red"); punto(2,2, "blue")

 # Ho ottenuto la figura a sinistra. Ecco come ottenere quella a destra.
# Vedi fra due righe la spiegazione.
PIANO(0,10, 0,10); x <- c(1,4,8); y <- c(6,2,5)
cerchio3p(x,y, "black"); punti(x,y,"orange")
# Nel primo caso ho tracciato il cerchio di centro (2,2) e raggio 1.5 in rosso ("red");
# ho anche tracciato in blu ("blue") il punto che corrisponde al centro.
# Nel secondo caso ho tracciato il cerchio passante per 3 punti, dei quali ho messo le
# coordinate in x e in y; poi ho tracciato i punti di coordinate x ed y.
# Le figure appaiono in finestre sovrapposte. Per vedere la vecchia figura posso
# spostare la nuova finestra come scritto sopra, in (12).
# Volendo posso avere le coordinate del centro e il raggio del cerchio così tracciato:
centro3p; raggio3p
# [1] 4.5 5.5
# [1] 3.535534
# Il pallino piccolo rosso (nel centro ora calcolato) l'ho tracciato col comando Punti:
Punti(4.5, 5.5, "red") # potevo usare anche Punto
# Col comando PUNTI (o PUNTO) si tracciano pallini leggermente più grandi; con Punt o
# punt leggeremente più piccoli.
#
# (14) Con Piano(0,10,0,20) (con la sola iniziale, "P", maiuscola) le x e le y sono
# rappresentate con scale che possono essere diverse: modificando la finestra la forma
# della figura disegnata cambia. Ecco come può apparire l'ultimo cerchio.
Piano(0,10,0,20); cerchio3p(x,y, "violet")
Piano(0,15,0,10); cerchio3p(x,y, "brown")
# Ho ottenuto la figura a sinistra. Ecco come ottenere quella a destra.
# Vedi fra due righe la spiegazione.
PIANO(0,10, 0,10); x <- c(1,4,8); y <- c(6,2,5)
cerchio3p(x,y, "black"); punti(x,y,"orange")
# Nel primo caso ho tracciato il cerchio di centro (2,2) e raggio 1.5 in rosso ("red");
# ho anche tracciato in blu ("blue") il punto che corrisponde al centro.
# Nel secondo caso ho tracciato il cerchio passante per 3 punti, dei quali ho messo le
# coordinate in x e in y; poi ho tracciato i punti di coordinate x ed y.
# Le figure appaiono in finestre sovrapposte. Per vedere la vecchia figura posso
# spostare la nuova finestra come scritto sopra, in (12).
# Volendo posso avere le coordinate del centro e il raggio del cerchio così tracciato:
centro3p; raggio3p
# [1] 4.5 5.5
# [1] 3.535534
# Il pallino piccolo rosso (nel centro ora calcolato) l'ho tracciato col comando Punti:
Punti(4.5, 5.5, "red") # potevo usare anche Punto
# Col comando PUNTI (o PUNTO) si tracciano pallini leggermente più grandi; con Punt o
# punt leggeremente più piccoli.
#
# (14) Con Piano(0,10,0,20) (con la sola iniziale, "P", maiuscola) le x e le y sono
# rappresentate con scale che possono essere diverse: modificando la finestra la forma
# della figura disegnata cambia. Ecco come può apparire l'ultimo cerchio.
Piano(0,10,0,20); cerchio3p(x,y, "violet")
Piano(0,15,0,10); cerchio3p(x,y, "brown")
 # Volendo posso evidenziare le coordinate di un qualunque punto dello schermo. Battendo:
xy(2)
# e cliccando nel punto sopra evidenziato con una croce, ottengo:
# [1] 4.5 5.5
# l'arrotondamento a 2 cifre. Se voglio ad es. 3 cifre batto xy(3)
#
# I nomi dei colori sono in inglese. Eccone alcuni:
# Volendo posso evidenziare le coordinate di un qualunque punto dello schermo. Battendo:
xy(2)
# e cliccando nel punto sopra evidenziato con una croce, ottengo:
# [1] 4.5 5.5
# l'arrotondamento a 2 cifre. Se voglio ad es. 3 cifre batto xy(3)
#
# I nomi dei colori sono in inglese. Eccone alcuni:
 # 1 black 2 grey 3 white 4 brown 5 orange 6 red 7 pink
# ( nero grigio bianco marrone arancione rosso rosa )
# 8 violet 9 blue 10 cyan 11 yellow 12 green 13 seagreen
# ( viola blu ciano giallo verde verde mare )
# Puoi comunque richiamare i nomi di un po' di colori col comando Colori()
# NOTA: al posto di "black" (colore "nero") puoi usare il numero 1:
# con cerchio3p(x,y, 1) avresti ottenuto la figura in nero
#
# (15) Vediamo come tracciare alcune figure geometriche in un sistema monometrico,
# cioè in una parte di piano rappresentata con le stesse unità per i due assi, ossia
# con il comando PIANO, introdotto sopra nel punto (10).
PIANO(0,10,0,10)
cerchio(2,8, 2, "red")
punto(6,7, "blue"); punto(4,5,"blue"); retta2p(6,7, 4,5, "blue")
segm(8,7, 8,5, "black"); segm(4,3, 6,3, "black")
punto(4,0, "brown"); punto(8,3, "brown"); semiretta(4,0, 8,3, "brown")
Segm(7,1, 10,2, "orange") # Con Segm ottengo segmenti più spessi
# Con linea li avrei sottili
# Per tracciare segmenti dato il punto inziale e la direzione vedi il punto (16)
# 1 black 2 grey 3 white 4 brown 5 orange 6 red 7 pink
# ( nero grigio bianco marrone arancione rosso rosa )
# 8 violet 9 blue 10 cyan 11 yellow 12 green 13 seagreen
# ( viola blu ciano giallo verde verde mare )
# Puoi comunque richiamare i nomi di un po' di colori col comando Colori()
# NOTA: al posto di "black" (colore "nero") puoi usare il numero 1:
# con cerchio3p(x,y, 1) avresti ottenuto la figura in nero
#
# (15) Vediamo come tracciare alcune figure geometriche in un sistema monometrico,
# cioè in una parte di piano rappresentata con le stesse unità per i due assi, ossia
# con il comando PIANO, introdotto sopra nel punto (10).
PIANO(0,10,0,10)
cerchio(2,8, 2, "red")
punto(6,7, "blue"); punto(4,5,"blue"); retta2p(6,7, 4,5, "blue")
segm(8,7, 8,5, "black"); segm(4,3, 6,3, "black")
punto(4,0, "brown"); punto(8,3, "brown"); semiretta(4,0, 8,3, "brown")
Segm(7,1, 10,2, "orange") # Con Segm ottengo segmenti più spessi
# Con linea li avrei sottili
# Per tracciare segmenti dato il punto inziale e la direzione vedi il punto (16)
 # Se uso un sistema non monometrico [vedi (14)] forme ed angoli appaiono diversi.
# Posso ottenere i grafici senza griglia, come quello sopra a destra: basta che usi
# PIANOS e PianoS invece di PIANO e Piano. Con PIANOs e Pianos non ho neanche gli
# assi. Con PIANOss e Pianoss non ho neanche la scritta delle coordinate.
# Con GRIGLIA e Griglia invece di PIANO e Piano viene rappresentata solo la griglia,
# senza l'indicazione delle coordinate. Con GRIGLIAs e Griglias non ho gli assi. Ecco
# cosa apparirebbe se, prima dei comandi precedenti, invece di PIANO(0,10, 0,10) usassi
# GRIGLIA(0,10, 0,10):
# Se uso un sistema non monometrico [vedi (14)] forme ed angoli appaiono diversi.
# Posso ottenere i grafici senza griglia, come quello sopra a destra: basta che usi
# PIANOS e PianoS invece di PIANO e Piano. Con PIANOs e Pianos non ho neanche gli
# assi. Con PIANOss e Pianoss non ho neanche la scritta delle coordinate.
# Con GRIGLIA e Griglia invece di PIANO e Piano viene rappresentata solo la griglia,
# senza l'indicazione delle coordinate. Con GRIGLIAs e Griglias non ho gli assi. Ecco
# cosa apparirebbe se, prima dei comandi precedenti, invece di PIANO(0,10, 0,10) usassi
# GRIGLIA(0,10, 0,10):
 # Il comando medio2p traccia il punto medio di 2 punti. asse2p traccia l'asse del
# segmento che ha per estremi 2 punti.
PIANO(0,10,0,10)
punto(5,1, "red"); punto(8,6, "red"); punto(8,3, "red")
medio2p(8,6, 8,3, "blue"); medio2p(5,1, 8,3, "blue") # 1ª figura
asse2p(8,6, 8,3, "brown"); asse2p(5,1, 8,3, "brown") # 2ª figura
cerchio3p(c(5,8,8), c(1,3,6), "grey")
centro3p
# [1] 4.833333 4.500000
PUNTI(4.833333,4.500000, "green") # 3ª figura
# Il comando medio2p traccia il punto medio di 2 punti. asse2p traccia l'asse del
# segmento che ha per estremi 2 punti.
PIANO(0,10,0,10)
punto(5,1, "red"); punto(8,6, "red"); punto(8,3, "red")
medio2p(8,6, 8,3, "blue"); medio2p(5,1, 8,3, "blue") # 1ª figura
asse2p(8,6, 8,3, "brown"); asse2p(5,1, 8,3, "brown") # 2ª figura
cerchio3p(c(5,8,8), c(1,3,6), "grey")
centro3p
# [1] 4.833333 4.500000
PUNTI(4.833333,4.500000, "green") # 3ª figura
 # Usando grigliaO, grigliaV, GrigliaO, GrigliaV posso tracciare griglie a piacere:
PIANOs(0,100, 0,100)
grigliaO( seq(0,100,10) ); grigliaV( seq(0,100,10) )
GrigliaO( seq(0,100,50) ); GrigliaV( seq(0,100,50) )
# Usando grigliaO, grigliaV, GrigliaO, GrigliaV posso tracciare griglie a piacere:
PIANOs(0,100, 0,100)
grigliaO( seq(0,100,10) ); grigliaV( seq(0,100,10) )
GrigliaO( seq(0,100,50) ); GrigliaV( seq(0,100,50) )
 # Con GrigliaO e GrigliaV i tratti sono più lunghi e blu scuro, con grigliaO e grigliaV
# i colori possono essere cambiati usando coltrat (vedi punto 22). Sopra a destra ciò
# che si ottiene se si è impostato coltrat="cyan4" (ciano scuro).
#
# (16) Altre figure. Alcune spezzate; la loro lunghezza; la inclinazione di una
# retta passante per 2 punti; la pendenza della retta di una data inclinazione (il
# rapporto tra l'innalzamento e l'avanzamento se si procede con quella inclinazione);
# l'inclinazione di una retta con data pendenza.
PIANO(-3,9,-2,10)
x <- c(-3,2,8,8); y <- c(1,1,9,-1)
spezzata(x,y, "green"); punti(x,y, "red")
lung(x,y)
# [1] 25
inclinazione(2,1, 8,9) # la incl. (in °) della retta per (2,1) e (8,9)
# [1] 53.1301
pendenza(53.1301) # la pendenza di una retta inclinata di 53.1301°
# [1] 1.333333
inclinazione2(11/100) # la incl. (in °) di una retta con pendenza dell'11%
# [1] 6.277298
x1 <- c(-2,2,2,-2); y1 <- c(6,6,10,10)
spezzata(x1,y1,"grey"); punti(x1,y1,"blue") # Vedi figura 1
1
# Con GrigliaO e GrigliaV i tratti sono più lunghi e blu scuro, con grigliaO e grigliaV
# i colori possono essere cambiati usando coltrat (vedi punto 22). Sopra a destra ciò
# che si ottiene se si è impostato coltrat="cyan4" (ciano scuro).
#
# (16) Altre figure. Alcune spezzate; la loro lunghezza; la inclinazione di una
# retta passante per 2 punti; la pendenza della retta di una data inclinazione (il
# rapporto tra l'innalzamento e l'avanzamento se si procede con quella inclinazione);
# l'inclinazione di una retta con data pendenza.
PIANO(-3,9,-2,10)
x <- c(-3,2,8,8); y <- c(1,1,9,-1)
spezzata(x,y, "green"); punti(x,y, "red")
lung(x,y)
# [1] 25
inclinazione(2,1, 8,9) # la incl. (in °) della retta per (2,1) e (8,9)
# [1] 53.1301
pendenza(53.1301) # la pendenza di una retta inclinata di 53.1301°
# [1] 1.333333
inclinazione2(11/100) # la incl. (in °) di una retta con pendenza dell'11%
# [1] 6.277298
x1 <- c(-2,2,2,-2); y1 <- c(6,6,10,10)
spezzata(x1,y1,"grey"); punti(x1,y1,"blue") # Vedi figura 1
1  2
2  3
3  # Poi chiudiamo ogni spezzata (spezzaC) colorandola e calcoliamo l'area del poligono
# ottenuto (vedi figura 2);
spezzaC(x,y,"yellow"); punti(x,y,"red")
spezzaC(x1,y1,"grey"); punti(x1,y1,"orange")
areaPol(x,y); areaPol(x1,y1)
# [1] 35
# [1] 16
# La figura 3 è stata costruita tracciando la spezzata con una linea sottile, mediante
# il comando spezza, e due frecce:
PIANO(-3,9,-2,10); spezza(x,y, "black"); Punti(x,y, "blue")
freccia(-2,4, 2,8, "red"); freccia(2,8, 4,6, "red")
# L'analogo comando frec traccia frecce più sottili.
# Col comando dirFreccia calcolo direzione e lunghezza di una freccia di cui siano
# dati i punti iniziale e finale:
dirFreccia(-2,4, 2,8)
# direz. = 45 ° lungh. = 5.656854
dirFreccia(2,8, 4,6)
# direz. = 315 ° lungh. = 2.828427
# Con dirFreccia1 e dirFreccia2 ho direzione (in °) e lunghezza:
dirFreccia1(-2,4, 2,8); dirFreccia2(-2,4, 2,8)
# 45 5.656854
# Con Freccia e Frec traccio le frecce dando in input direzione e lunghezza:
Freccia(-2,4, 45, 5.656854, "blue") # ho stesso esito di freccia(-2,4, 2,8, "red")
# Con Frecciax e Frecciay ho le coordinate delle punte:
Frecciax(-2,4, 45, 5.656854); Frecciay(-2,4, 45, 5.656854)
# 2 8
# Nella figura sono tracciati anche segmenti che partono da un punto x,y e proseguono
# in una direzione dir per una distanza d con Direzione(x,y, dir, d, col)
Direzione(-1,-2, 0, 5, "orange"); Direzione(-1,-2, 30, 5, "orange")
Direzione(-1,-2, 60, 5, "orange"); Direzionex; Punti(Direzionex,Direzioney, "brown")
# [1] 1.5
# Direzionex e Direzioney contengono le coordinate dei punti di arrivo. Direzio traccia
# i segmenti con linee più sottili rispetto a Direzione. Se metto il colore 0 il segm.
# non è tracciato, ma in Direzionex e Direzioney ho le coordinate dei punti di arrivo.
#
# punto_punto e punto_retta calcolano la distanza tra 2 punti e tra 1 punto e la retta
# passante per 2 punti dati.
PIANO(-3,9,-2,10)
PUNTO(2,1,"red"); PUNTO(8,9,"red"); PUNTO(8,-1,"orange")
punto_punto(2,1, 8,9)
# [1] 10
retta2p(2,1, 8,9, "blue")
punto_retta(8,-1, 2,1, 8,9)
# [1] 6
# Vedi fig. A (i due punti rossi e la retta, blu, per essi; il punto arancione)
# Poi chiudiamo ogni spezzata (spezzaC) colorandola e calcoliamo l'area del poligono
# ottenuto (vedi figura 2);
spezzaC(x,y,"yellow"); punti(x,y,"red")
spezzaC(x1,y1,"grey"); punti(x1,y1,"orange")
areaPol(x,y); areaPol(x1,y1)
# [1] 35
# [1] 16
# La figura 3 è stata costruita tracciando la spezzata con una linea sottile, mediante
# il comando spezza, e due frecce:
PIANO(-3,9,-2,10); spezza(x,y, "black"); Punti(x,y, "blue")
freccia(-2,4, 2,8, "red"); freccia(2,8, 4,6, "red")
# L'analogo comando frec traccia frecce più sottili.
# Col comando dirFreccia calcolo direzione e lunghezza di una freccia di cui siano
# dati i punti iniziale e finale:
dirFreccia(-2,4, 2,8)
# direz. = 45 ° lungh. = 5.656854
dirFreccia(2,8, 4,6)
# direz. = 315 ° lungh. = 2.828427
# Con dirFreccia1 e dirFreccia2 ho direzione (in °) e lunghezza:
dirFreccia1(-2,4, 2,8); dirFreccia2(-2,4, 2,8)
# 45 5.656854
# Con Freccia e Frec traccio le frecce dando in input direzione e lunghezza:
Freccia(-2,4, 45, 5.656854, "blue") # ho stesso esito di freccia(-2,4, 2,8, "red")
# Con Frecciax e Frecciay ho le coordinate delle punte:
Frecciax(-2,4, 45, 5.656854); Frecciay(-2,4, 45, 5.656854)
# 2 8
# Nella figura sono tracciati anche segmenti che partono da un punto x,y e proseguono
# in una direzione dir per una distanza d con Direzione(x,y, dir, d, col)
Direzione(-1,-2, 0, 5, "orange"); Direzione(-1,-2, 30, 5, "orange")
Direzione(-1,-2, 60, 5, "orange"); Direzionex; Punti(Direzionex,Direzioney, "brown")
# [1] 1.5
# Direzionex e Direzioney contengono le coordinate dei punti di arrivo. Direzio traccia
# i segmenti con linee più sottili rispetto a Direzione. Se metto il colore 0 il segm.
# non è tracciato, ma in Direzionex e Direzioney ho le coordinate dei punti di arrivo.
#
# punto_punto e punto_retta calcolano la distanza tra 2 punti e tra 1 punto e la retta
# passante per 2 punti dati.
PIANO(-3,9,-2,10)
PUNTO(2,1,"red"); PUNTO(8,9,"red"); PUNTO(8,-1,"orange")
punto_punto(2,1, 8,9)
# [1] 10
retta2p(2,1, 8,9, "blue")
punto_retta(8,-1, 2,1, 8,9)
# [1] 6
# Vedi fig. A (i due punti rossi e la retta, blu, per essi; il punto arancione)
 # retta_retta(x,y, x1,y1, p,q, p1,q1) trova l'intersezione della retta per x,y e
# x1,y1 e di quella per p,q e p1,q1. Coi comandi seguenti ottengo B: ho tracciato i
# punti verdi e la retta marrone passante per essi, e l'ho intersecata con quella blu.
PUNTO(2,-1,"green"); PUNTO(8,7,"green")
retta2p(2,-1, 8,7, "brown")
retta_retta(2,-1, 8,7, 2,1, 8,9)
# [1] "rette parallele"
# Il programma mi dice che le due rette sono parallele. Provo con un'altra retta:
# quella che va dal punto arancione al punto che indicherò col colore viola.
# Dare colori diversi alle figure mi facilita ritrovare i comandi in cui le ho usate.
PUNTO(4,10, "magenta")
retta2p(8,-1, 4,10, "grey")
retta_retta(8,-1, 4,10, 2,1, 8,9)
# [1] 5.551020 5.734694
PUNTO(5.551020, 5.734694, "black")
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta metto noStampa=1 ]
# Ho ottenuto come intersezione il pallino nero che si vede nella figura C.
# Ora provo a tracciare la perpendicolare alla retta blu che parte da 8,-1: uso il
# comando punto_retta2 (che opera come punto_retta ma invece di calcolare la distanza
# punto-retta trova le coordinate del punto di minima distanza) per trovare il punto di
# intersezione; traccio sia la semiretta che il segmento: figura D.
punto_retta2(8,-1, 2,1,8,9)
# [1] 3.2 2.6
semiretta(8,-1, 3.2,2.6, "yellow")
segm(8,-1, 3.2,2.6, "red")
PUNTO(3.2,2.6, "brown")
# Potevo procedere anche intersecando due rette descritte come "punto-direzione":
# (intersezione tra la retta blu e quella giallo-rossa)
inclinazione(2,1, 8,9)
# [1] 53.1301
retta_retta2(2,1, 53.1301, 8,-1, 53.1301+90)
# [1] 3.2 2.6
# retta_retta2(x,y, d1, p,q, d2) trova l'intersezione della retta per x,y e direzione
# d1 e di quella per p,q e direzione d2
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta2 metto noStampa=1 ]
# Per tracciare una retta, oltre al comando retta2p (che traccia la retta per due punti)
# posso usare il comando punto_inclina(x,y, dir, col) che traccia la retta per x,y
# inclinata nella direzione dir; punto_incl la traccia sottile. Esempi:
PIANO(-1,9, -2,8); PUNTO(5,4, "black")
punto_inclina(5,4, 45, "brown"); punto_inclina(5,4, 90, "red")
punto_incl(5,4, 150, "black"); punto_incl(5,4, 0, "magenta")
PUNTO(5,4, "black")
# retta_retta(x,y, x1,y1, p,q, p1,q1) trova l'intersezione della retta per x,y e
# x1,y1 e di quella per p,q e p1,q1. Coi comandi seguenti ottengo B: ho tracciato i
# punti verdi e la retta marrone passante per essi, e l'ho intersecata con quella blu.
PUNTO(2,-1,"green"); PUNTO(8,7,"green")
retta2p(2,-1, 8,7, "brown")
retta_retta(2,-1, 8,7, 2,1, 8,9)
# [1] "rette parallele"
# Il programma mi dice che le due rette sono parallele. Provo con un'altra retta:
# quella che va dal punto arancione al punto che indicherò col colore viola.
# Dare colori diversi alle figure mi facilita ritrovare i comandi in cui le ho usate.
PUNTO(4,10, "magenta")
retta2p(8,-1, 4,10, "grey")
retta_retta(8,-1, 4,10, 2,1, 8,9)
# [1] 5.551020 5.734694
PUNTO(5.551020, 5.734694, "black")
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta metto noStampa=1 ]
# Ho ottenuto come intersezione il pallino nero che si vede nella figura C.
# Ora provo a tracciare la perpendicolare alla retta blu che parte da 8,-1: uso il
# comando punto_retta2 (che opera come punto_retta ma invece di calcolare la distanza
# punto-retta trova le coordinate del punto di minima distanza) per trovare il punto di
# intersezione; traccio sia la semiretta che il segmento: figura D.
punto_retta2(8,-1, 2,1,8,9)
# [1] 3.2 2.6
semiretta(8,-1, 3.2,2.6, "yellow")
segm(8,-1, 3.2,2.6, "red")
PUNTO(3.2,2.6, "brown")
# Potevo procedere anche intersecando due rette descritte come "punto-direzione":
# (intersezione tra la retta blu e quella giallo-rossa)
inclinazione(2,1, 8,9)
# [1] 53.1301
retta_retta2(2,1, 53.1301, 8,-1, 53.1301+90)
# [1] 3.2 2.6
# retta_retta2(x,y, d1, p,q, d2) trova l'intersezione della retta per x,y e direzione
# d1 e di quella per p,q e direzione d2
# [ volendo posso memorizzare direttamente le coordinate del punto con
# x=soluzione[1]; y=soluzione[2]; PUNTO(x,y, "black")
# Se non voglio visualizzare i valori prima di retta_retta2 metto noStampa=1 ]
# Per tracciare una retta, oltre al comando retta2p (che traccia la retta per due punti)
# posso usare il comando punto_inclina(x,y, dir, col) che traccia la retta per x,y
# inclinata nella direzione dir; punto_incl la traccia sottile. Esempi:
PIANO(-1,9, -2,8); PUNTO(5,4, "black")
punto_inclina(5,4, 45, "brown"); punto_inclina(5,4, 90, "red")
punto_incl(5,4, 150, "black"); punto_incl(5,4, 0, "magenta")
PUNTO(5,4, "black")
 # cerchio_cerchio(x1,y1,r1, x2,y2,r2) trova le eventuali intersezioni tra il cerchio
# di centro x1,y1 e raggio r1 e quello di centro x2,y2 e raggio r2. Esempi:
# cerchio_cerchio(x1,y1,r1, x2,y2,r2) trova le eventuali intersezioni tra il cerchio
# di centro x1,y1 e raggio r1 e quello di centro x2,y2 e raggio r2. Esempi:
 PIANO(-4,7,-3,8)
cerchio(0,4, 3,"brown")
cerchio(0,-1, 2,"red"); cerchio_cerchio(0,4,3, 0,-1,2)
# [1] 0 1
cerchio(4,-1, 1.5,"seagreen"); cerchio_cerchio(0,4,3, 4,-1,1.5)
# [1] "troppo distanti"
cerchio(4,6, 2,"blue"); cerchio_cerchio(0,4,3, 4,6,2)
# [1] 2.012660 6.224679 2.987340 4.275321
P=cerchio_cerchio(0,4,3, 4,6,2); PUNTO(P[1],P[2], "orange")
#
# Ecco come tracciare un poligono regolare di un certo numero N di lati con centro in
# C1,C2 inscritto nel cerchio di raggio R e un vertice con direzione G gradi:
# poligono(C1,C2, R, N,G, col). poligo lo traccia sottile, poligoC colora la parte
# interna invece del bordo.
BF=3; HF=3; PIANO(-1,5, -2,4)
punto(2,1, "blue"); cerchio(2,1, 3, "grey")
poligono(2,1, 3, 5,90, "red"); poligo(2,1, 2, 3,180, "brown")
poligo(4,3, 1, 4,0, "black"); poligoC(0,-1, 1, 4,45, "seagreen")
PIANO(-4,7,-3,8)
cerchio(0,4, 3,"brown")
cerchio(0,-1, 2,"red"); cerchio_cerchio(0,4,3, 0,-1,2)
# [1] 0 1
cerchio(4,-1, 1.5,"seagreen"); cerchio_cerchio(0,4,3, 4,-1,1.5)
# [1] "troppo distanti"
cerchio(4,6, 2,"blue"); cerchio_cerchio(0,4,3, 4,6,2)
# [1] 2.012660 6.224679 2.987340 4.275321
P=cerchio_cerchio(0,4,3, 4,6,2); PUNTO(P[1],P[2], "orange")
#
# Ecco come tracciare un poligono regolare di un certo numero N di lati con centro in
# C1,C2 inscritto nel cerchio di raggio R e un vertice con direzione G gradi:
# poligono(C1,C2, R, N,G, col). poligo lo traccia sottile, poligoC colora la parte
# interna invece del bordo.
BF=3; HF=3; PIANO(-1,5, -2,4)
punto(2,1, "blue"); cerchio(2,1, 3, "grey")
poligono(2,1, 3, 5,90, "red"); poligo(2,1, 2, 3,180, "brown")
poligo(4,3, 1, 4,0, "black"); poligoC(0,-1, 1, 4,45, "seagreen")
 #
# (17) Posso misurare le ampiezze degli angoli.
# Posso inserire scritte centrate in un punto a piacere. Un esempio.
PIANO(-1,5, -2.5,3.5)
punto(4,-2,"brown"); punto(1,1,"brown"); punto(4,3,"brown")
semiretta(1,1, 4,-2, "brown"); semiretta(1,1, 4,3,"brown")
scrivi(3.5,-2.5, "A"); scrivi(1/2,1/2, "B"); scrivi(3.5,3.5, "C")
#
# (17) Posso misurare le ampiezze degli angoli.
# Posso inserire scritte centrate in un punto a piacere. Un esempio.
PIANO(-1,5, -2.5,3.5)
punto(4,-2,"brown"); punto(1,1,"brown"); punto(4,3,"brown")
semiretta(1,1, 4,-2, "brown"); semiretta(1,1, 4,3,"brown")
scrivi(3.5,-2.5, "A"); scrivi(1/2,1/2, "B"); scrivi(3.5,3.5, "C")
 # Se voglio, come si è visto in (13), posso memorizzare i punti con un unico nome:
A=c(4,-2); B=c(1,1); C=c(4,3)
punto(A[1],A[2],"brown"); punto(B[1],B[2],"brown"); punto(C[1],C[2],"brown")
semiretta(B[1],B[2], A[1],A[2],"brown"); semiretta(B[1],B[2], C[1],C[2],"brown")
scrivi(A[1]-1/2,A[2]-1/2, "A"); scrivi(B[1]-1/2,B[2]-1/2,"B")
scrivi(C[1]-1/2,C[2]+1/2,"C")
# Misuro l'angolo ABC
angolo(A,B,C); round( angolo(A,B,C),0 )
# [1] 78.69007
# [1] 79
scrivi(2,1,"79°")
# L'angolo ABC è quello che ha vertice in B, primo lato BA e lato seguente in verso
# antiorario BC. L'angolo che va da BC a BA è indicato CBA:
angolo(C,B,A); round( angolo(C,B,A),0 )
# [1] 281.3099
# [1] 281
angolo(A,B,C)+angolo(C,B,A)
# 360
#
# Posso segnare facilmente dei punti su un cerchio dandone l'angolo che ne esprime la
# direzione in cui sono raggiungibili dal centro. Se dò il cerchio - vedi punto (13) -
# mediante centro e raggio uso i comandi cerchioA (li segno) o cerchioA2 (ne stampo le
# coordinate):
PIANO(0,4, 0,4)
cerchio(2,2, 1.5, "red")
cerchioA2(2,2, 1.5, 45)
[1] 3.06066 3.06066
cerchioA(2,2, 1.5, 45, "blue")
ang=c(90,90+45,180,180+45,270,270+45,0); cerchioA(2,2, 1.5, ang, "black")
# Vedi la figura sotto a sinistra.
# Se dò il cerchio mediante 3 punti uso i comandi cerchio3pA o cerchio3pA2:
PIANO(0,10, 0,10)
x <- c(1,4,8); y <- c(6,2,5); cerchio3p(x,y, "black")
cerchio3pA2(x,y, 90)
[1] 4.500000 9.035534
cerchio3pA(x,y, ang, "red") # vedi la figura al centro
# Se voglio, come si è visto in (13), posso memorizzare i punti con un unico nome:
A=c(4,-2); B=c(1,1); C=c(4,3)
punto(A[1],A[2],"brown"); punto(B[1],B[2],"brown"); punto(C[1],C[2],"brown")
semiretta(B[1],B[2], A[1],A[2],"brown"); semiretta(B[1],B[2], C[1],C[2],"brown")
scrivi(A[1]-1/2,A[2]-1/2, "A"); scrivi(B[1]-1/2,B[2]-1/2,"B")
scrivi(C[1]-1/2,C[2]+1/2,"C")
# Misuro l'angolo ABC
angolo(A,B,C); round( angolo(A,B,C),0 )
# [1] 78.69007
# [1] 79
scrivi(2,1,"79°")
# L'angolo ABC è quello che ha vertice in B, primo lato BA e lato seguente in verso
# antiorario BC. L'angolo che va da BC a BA è indicato CBA:
angolo(C,B,A); round( angolo(C,B,A),0 )
# [1] 281.3099
# [1] 281
angolo(A,B,C)+angolo(C,B,A)
# 360
#
# Posso segnare facilmente dei punti su un cerchio dandone l'angolo che ne esprime la
# direzione in cui sono raggiungibili dal centro. Se dò il cerchio - vedi punto (13) -
# mediante centro e raggio uso i comandi cerchioA (li segno) o cerchioA2 (ne stampo le
# coordinate):
PIANO(0,4, 0,4)
cerchio(2,2, 1.5, "red")
cerchioA2(2,2, 1.5, 45)
[1] 3.06066 3.06066
cerchioA(2,2, 1.5, 45, "blue")
ang=c(90,90+45,180,180+45,270,270+45,0); cerchioA(2,2, 1.5, ang, "black")
# Vedi la figura sotto a sinistra.
# Se dò il cerchio mediante 3 punti uso i comandi cerchio3pA o cerchio3pA2:
PIANO(0,10, 0,10)
x <- c(1,4,8); y <- c(6,2,5); cerchio3p(x,y, "black")
cerchio3pA2(x,y, 90)
[1] 4.500000 9.035534
cerchio3pA(x,y, ang, "red") # vedi la figura al centro
 # Sono comodi per individuare i punti di un cerchio anche i comandi xrot(a) e yrot(a)
# che dato un angolo a (in gradi) danno ascissa e ordinata dei punti del cerchio di
# centro 0,0 e raggio 1 raggiungibili dal centro muovendosi in direzione a.
# Sopra a destra i punti nelle direzioni 0°, 10°, 20°, 30°, ...
PIANO(-1,1, -1,1)
a=seq(0,360, 10); PUNTO( xrot(a),yrot(a), "brown" )
#
# Sappiamo che, con riga, goniometro e compasso, per costruire un triangolo mi basta
# conoscere i tre lati o due lati e l'angolo compreso o due angoli e il lato compreso.
# Qui posso costruirli usando i comandi triLLL(L1,L2,L3), triLAL(L1,A,L2) e
# triALA(A1,L,A2). Battendo LATI e ANGOLI ho le misure dei lati e degli angoli ad essi
# opposti, con TRIANGOLO() ho l'immagine del triangolo [per costruire poligoni più
# generali vedi il comando spezzata nel paragrafo precedente]
triLLL(5,5,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 5 60 60 60
triLAL(5,90,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 7.071068 45 45 90
triALA(30,8,45)
LATI; ANGOLI; TRIANGOLO()
# 5.856406 4.141105 8 45 30 105 (al lato 5.856… è opposto l'angolo di 45°, ecc.)
# Sono comodi per individuare i punti di un cerchio anche i comandi xrot(a) e yrot(a)
# che dato un angolo a (in gradi) danno ascissa e ordinata dei punti del cerchio di
# centro 0,0 e raggio 1 raggiungibili dal centro muovendosi in direzione a.
# Sopra a destra i punti nelle direzioni 0°, 10°, 20°, 30°, ...
PIANO(-1,1, -1,1)
a=seq(0,360, 10); PUNTO( xrot(a),yrot(a), "brown" )
#
# Sappiamo che, con riga, goniometro e compasso, per costruire un triangolo mi basta
# conoscere i tre lati o due lati e l'angolo compreso o due angoli e il lato compreso.
# Qui posso costruirli usando i comandi triLLL(L1,L2,L3), triLAL(L1,A,L2) e
# triALA(A1,L,A2). Battendo LATI e ANGOLI ho le misure dei lati e degli angoli ad essi
# opposti, con TRIANGOLO() ho l'immagine del triangolo [per costruire poligoni più
# generali vedi il comando spezzata nel paragrafo precedente]
triLLL(5,5,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 5 60 60 60
triLAL(5,90,5)
LATI; ANGOLI; TRIANGOLO()
# 5 5 7.071068 45 45 90
triALA(30,8,45)
LATI; ANGOLI; TRIANGOLO()
# 5.856406 4.141105 8 45 30 105 (al lato 5.856… è opposto l'angolo di 45°, ecc.)
 #
# (18) Come realizzare il grafico di un fenomeno al variare di un altro:
# consumo medio di kg di frutta fresca all'anno consumata da un italiano.
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
# max e min - vedi il punto (20) successivo - sono utili per scegliere il "Piano"
# (qui trovo che il massimo è 88 e quindi faccio variare la y tra 0 e 90)
max(frutta)
# [1] 88
BF=4; HF=2.5
Piano(1880,1980, 0,90) # Uso "Piano" [→(14)] per avere unità diverse sui due assi
spezzata(anni,frutta, "blue"); punti(anni,frutta,"brown")
#
# (18) Come realizzare il grafico di un fenomeno al variare di un altro:
# consumo medio di kg di frutta fresca all'anno consumata da un italiano.
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
# max e min - vedi il punto (20) successivo - sono utili per scegliere il "Piano"
# (qui trovo che il massimo è 88 e quindi faccio variare la y tra 0 e 90)
max(frutta)
# [1] 88
BF=4; HF=2.5
Piano(1880,1980, 0,90) # Uso "Piano" [→(14)] per avere unità diverse sui due assi
spezzata(anni,frutta, "blue"); punti(anni,frutta,"brown")
 # Sono state messe anche delle scritte lungo gli assi con:
suassex("anni"); suassey("frutta")
#
# (19) Gli abitanti (in migliaia) del Nord, del Centro e del Mezzogiorno:
# I comandi più semplici:
N = 25755; C = 12068; S = 20843; Italia = c(N,C,S)
Barre2(Italia); torta2(Italia); Striscia2(Italia)
# % 43.90107 20.57069 35.52824
# Sono state messe anche delle scritte lungo gli assi con:
suassex("anni"); suassey("frutta")
#
# (19) Gli abitanti (in migliaia) del Nord, del Centro e del Mezzogiorno:
# I comandi più semplici:
N = 25755; C = 12068; S = 20843; Italia = c(N,C,S)
Barre2(Italia); torta2(Italia); Striscia2(Italia)
# % 43.90107 20.57069 35.52824
 HF=2; BF=2
torta(Italia) # diagramma a torta con le tacche dei centesimi
Torta(Italia) # diagramma a torta senza tacche
Tortam(Italia) # diagramma a mezza torta
HF=2; BF=2
torta(Italia) # diagramma a torta con le tacche dei centesimi
Torta(Italia) # diagramma a torta senza tacche
Tortam(Italia) # diagramma a mezza torta
 # giallo,celeste,... % 43.90107 20.57069 35.52824
# Per ottenere la distribuzione percentuale arrotondata - vedi il punto (07) - posso fare:
distribuzione(Italia, 0)
# 44 21 36
distribuzione(Italia, 2)
# 43.9 20.57 35.53 # se voglio poi scrivo 43.90 invece di 43.9
distribuzione(Italia, -1)
# 40 20 40
#
nomiBarre = c("N","C","S"); Barre(Italia)
# giallo,celeste,... % 43.90107 20.57069 35.52824
# Per ottenere la distribuzione percentuale arrotondata - vedi il punto (07) - posso fare:
distribuzione(Italia, 0)
# 44 21 36
distribuzione(Italia, 2)
# 43.9 20.57 35.53 # se voglio poi scrivo 43.90 invece di 43.9
distribuzione(Italia, -1)
# 40 20 40
#
nomiBarre = c("N","C","S"); Barre(Italia)
 # Il diagramma a destra è stato ottenuto scrivemdo prima noGriglia = 1
#
Striscia(Italia)
# Il diagramma a destra è stato ottenuto scrivemdo prima noGriglia = 1
#
Striscia(Italia)
 # Posso usare "nomi" anche per strisce e torte con nomiStriscia e nomiTorta. Es.:
nomi = c("N","C","S"); nomiTorta = nomi; torta(Italia)
giallo,celeste,... % 43.90107 20.57069 35.52824
giallo,celeste,... N C S
# Se voglio posso usare UNDER(nome,x) e ABOVE(nome,x) per mettere nomi sotto/sopra
# le barre; in x devo mettere il nome della barra. Metti 'UNDER("%",0.5)'
# se vuoi ''%' sotto l'asse y):
Bar( c(25755,12068,20843) ); ABOVE(25755,1); ABOVE(12068,2); ABOVE(20843,3)
UNDER("North",1); UNDER("Center",2); UNDER("South",3); UNDER("%",0)
# Posso usare "nomi" anche per strisce e torte con nomiStriscia e nomiTorta. Es.:
nomi = c("N","C","S"); nomiTorta = nomi; torta(Italia)
giallo,celeste,... % 43.90107 20.57069 35.52824
giallo,celeste,... N C S
# Se voglio posso usare UNDER(nome,x) e ABOVE(nome,x) per mettere nomi sotto/sopra
# le barre; in x devo mettere il nome della barra. Metti 'UNDER("%",0.5)'
# se vuoi ''%' sotto l'asse y):
Bar( c(25755,12068,20843) ); ABOVE(25755,1); ABOVE(12068,2); ABOVE(20843,3)
UNDER("North",1); UNDER("Center",2); UNDER("South",3); UNDER("%",0)
 # Posso mettere nomi sopra/sotto le strisce con above(nome,x), under(nome,x), under2(nome,x)
Striscia(c(25755,12068,20843)); above(25755,21); above(12068,53); above(20843,82)
# Posso mettere nomi sopra/sotto le strisce con above(nome,x), under(nome,x), under2(nome,x)
Striscia(c(25755,12068,20843)); above(25755,21); above(12068,53); above(20843,82)
 Striscia(c(25755,12068,20843)); above("North",21); above("Center",53); above("South",82)
under("Italy",25); under2("North-Center-South",25)
Striscia(c(25755,12068,20843)); above("North",21); above("Center",53); above("South",82)
under("Italy",25); under2("North-Center-South",25)
 #
# Una torta "vuota" ed un goniometro (il goniometro è il cerchio diviso in gradi (°),
torta(0); gonio() # cioè in 360 parti uguali).
GONIO(0) # Un quarto di goniometro
Striscia(0) # ed una striscia.
#
# Una torta "vuota" ed un goniometro (il goniometro è il cerchio diviso in gradi (°),
torta(0); gonio() # cioè in 360 parti uguali).
GONIO(0) # Un quarto di goniometro
Striscia(0) # ed una striscia.






 # con BF=3; HF=3; QUADRETTI(10,10) ho quadretti con lato di circa 5 mm
# Volendo posso aprire prima uno spazio e poi aggiungere i quadretti:
PIANOss(0,15,0,5); Quadretti(15,5)
# con BF=3; HF=3; QUADRETTI(10,10) ho quadretti con lato di circa 5 mm
# Volendo posso aprire prima uno spazio e poi aggiungere i quadretti:
PIANOss(0,15,0,5); Quadretti(15,5)

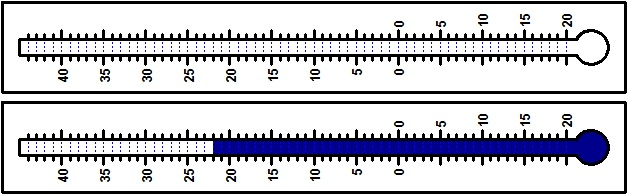
 # Altri diagrammi:
# Altri diagrammi:

 # Vedi qui. Si usano puntiO, puntiV e puntiD per tracciare i punti in varie forme.
#
# (20)
# Ecco come fare istogramma e calcoli relativi a singoli dati raccolti.
# Un esempio: le temperature alle ore 12 in un mese invernale di 31 giorni:
# (arrotondate agli interi)
T <- c(3,4,5,2,2,3,4,6,6,8,9,9,8,10,8,7,8,6,4,1,-1,3,5,7,6,9,12,11,14,13,13)
max(T);min(T)
# [1] 14
# [1] -1
# Posso controllare se i dati sono proprio 31 col comando length ("lunghezza"):
length(T)
# [1] 31
# Volendo ordinarli:
sort(T)
# [1] -1 1 2 2 3 3 3 4 4 4 5 5 6 6 6 6 7 7 8 8 8 8 9 9 9 10 11 12 13 13 14
#
isto(T)
# Vedi qui. Si usano puntiO, puntiV e puntiD per tracciare i punti in varie forme.
#
# (20)
# Ecco come fare istogramma e calcoli relativi a singoli dati raccolti.
# Un esempio: le temperature alle ore 12 in un mese invernale di 31 giorni:
# (arrotondate agli interi)
T <- c(3,4,5,2,2,3,4,6,6,8,9,9,8,10,8,7,8,6,4,1,-1,3,5,7,6,9,12,11,14,13,13)
max(T);min(T)
# [1] 14
# [1] -1
# Posso controllare se i dati sono proprio 31 col comando length ("lunghezza"):
length(T)
# [1] 31
# Volendo ordinarli:
sort(T)
# [1] -1 1 2 2 3 3 3 4 4 4 5 5 6 6 6 6 7 7 8 8 8 8 9 9 9 10 11 12 13 13 14
#
isto(T)
 # Frequenze e frequenze percentuali:
# 1, 1, 5, 5, 6, 7, 2, 4
# 3.23,3.23,16.13,16.13,19.35,22.58,6.45,12.9
# Per altre statistiche usa il comando altrestat()
# Se davanti al comando "istogramma" metto noClassi=1 invece degli estremi di
# tutte le classi appare l'intervallo complessivo e il numero delle classi
# (la cosa è comoda se le classi sono molte):
# Frequenze e frequenze percentuali:
# 1, 1, 5, 5, 6, 7, 2, 4
# 3.23,3.23,16.13,16.13,19.35,22.58,6.45,12.9
# Per altre statistiche usa il comando altrestat()
# Se davanti al comando "istogramma" metto noClassi=1 invece degli estremi di
# tutte le classi appare l'intervallo complessivo e il numero delle classi
# (la cosa è comoda se le classi sono molte):
 # A destra che cosa si ottiene se metto prima: noGriglia = 1
#
# Se invece di "isto" usi questo comando:
istogramma(T)
# compare anche:
# Per altre statistiche usa il comando altrestat()
# che elabora altre statistiche (che eventualmente studierai più avanti):
altrestat()
# A destra che cosa si ottiene se metto prima: noGriglia = 1
#
# Se invece di "isto" usi questo comando:
istogramma(T)
# compare anche:
# Per altre statistiche usa il comando altrestat()
# che elabora altre statistiche (che eventualmente studierai più avanti):
altrestat()
 # Min. 1st Qu. Median Mean 3rd Qu. Max.
# -1.000 4.000 6.000 6.613 9.000 14.000
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
# Minimo, 1° quartile (separazione tra il primo 25% dei dati e i successivi), mediana
# (o 2° quartile o 50° percentile), media, 3° quartile (o 75° percentile), massimo.
# Questo diagramma, dalla forma di una scatola ("box") con "baffi", è chiamato boxplot.
#
# Per la mediana e la media ("median" e "mean" in inglese) posso battere semplicemente
median(T); mean(T)
# [1] 6
# [1] 6.612903
# La mediana in questo caso è un numero intero in quanto i dati sono interi ed essa è
# il dato al centro dell'elenco (se sono 9 è il 5º) o immediatamente prima (se sono 8 è
# il 4º). La media invece è un numero qualunque, ottenuto facendo la somma dei dati e
# dividendola per la loro quantità. Se lanciassi molte volte un dado equo la mediana
# potrebbe essere 3 o 4, a seconda dei casi, mentre la media sarebbe vicina a 3.5.
#
# NOTA. Facendo l'istogramma i dati vengono classificati nei vari intervalli (che nell'
# esempio precedente andavano da -2 a 0, da 0 a 2, da 2 a 4, …) mettendo i numeri a
# confine tra i vari intervalli in quello a destra. Ad es. -1 viene messo tra -2 e 0
# mentre di fronte a 1,2,2 mentre 1 viene messo tra 0 e 2, 2,2 vengono messi tra 2 e 4,
# assieme a 3,3,3.
#
# Se vogliamo invece vedere il grafico delle temperature al passare dei giorni
# (che abbiamo visto variano tra -1° e 14°):
BF=5; HF=3; Piano(0,32, -2,15)
giorni = 1:31
spezzata(giorni,T, "red"); punti(giorni,T,"blue")
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# -1.000 4.000 6.000 6.613 9.000 14.000
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
# Minimo, 1° quartile (separazione tra il primo 25% dei dati e i successivi), mediana
# (o 2° quartile o 50° percentile), media, 3° quartile (o 75° percentile), massimo.
# Questo diagramma, dalla forma di una scatola ("box") con "baffi", è chiamato boxplot.
#
# Per la mediana e la media ("median" e "mean" in inglese) posso battere semplicemente
median(T); mean(T)
# [1] 6
# [1] 6.612903
# La mediana in questo caso è un numero intero in quanto i dati sono interi ed essa è
# il dato al centro dell'elenco (se sono 9 è il 5º) o immediatamente prima (se sono 8 è
# il 4º). La media invece è un numero qualunque, ottenuto facendo la somma dei dati e
# dividendola per la loro quantità. Se lanciassi molte volte un dado equo la mediana
# potrebbe essere 3 o 4, a seconda dei casi, mentre la media sarebbe vicina a 3.5.
#
# NOTA. Facendo l'istogramma i dati vengono classificati nei vari intervalli (che nell'
# esempio precedente andavano da -2 a 0, da 0 a 2, da 2 a 4, …) mettendo i numeri a
# confine tra i vari intervalli in quello a destra. Ad es. -1 viene messo tra -2 e 0
# mentre di fronte a 1,2,2 mentre 1 viene messo tra 0 e 2, 2,2 vengono messi tra 2 e 4,
# assieme a 3,3,3.
#
# Se vogliamo invece vedere il grafico delle temperature al passare dei giorni
# (che abbiamo visto variano tra -1° e 14°):
BF=5; HF=3; Piano(0,32, -2,15)
giorni = 1:31
spezzata(giorni,T, "red"); punti(giorni,T,"blue")
 # Ricordiamo che le misure erano arrotondate (3° indica che la temperatura esatta sta
# tra 2.5° e 3.5°: 3° è la misura arrotondata agli interi più vicina al valore esatto)
#
# Un altro esempio in cui vediamo come i comandi possono essere spezzati su più righe.
# Ecco le lunghezze di molte fave (ossia semi di fava) raccolte da una classe di
# alunni di 12 anni. Occorre copiare e incollare tutte le righe, da "fave <- c("
# alla riga finale ")".
#
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
#
istogramma(fave)
# Ricordiamo che le misure erano arrotondate (3° indica che la temperatura esatta sta
# tra 2.5° e 3.5°: 3° è la misura arrotondata agli interi più vicina al valore esatto)
#
# Un altro esempio in cui vediamo come i comandi possono essere spezzati su più righe.
# Ecco le lunghezze di molte fave (ossia semi di fava) raccolte da una classe di
# alunni di 12 anni. Occorre copiare e incollare tutte le righe, da "fave <- c("
# alla riga finale ")".
#
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
#
istogramma(fave)
 # Frequenze e frequenze percentuali:
# 2, 0, 0, 4, 24, 40, 64, 64, 38, 18, 2, 0, 4
# 0.77,0,0,1.54,9.23,15.38,24.62,24.62,14.62,6.92,0.77,0,1.54
# Per altre statistiche usa il comando altrestat()
mean(fave); median(fave)
# [1] 1.659
# [1] 1.65
altrestat()
# Frequenze e frequenze percentuali:
# 2, 0, 0, 4, 24, 40, 64, 64, 38, 18, 2, 0, 4
# 0.77,0,0,1.54,9.23,15.38,24.62,24.62,14.62,6.92,0.77,0,1.54
# Per altre statistiche usa il comando altrestat()
mean(fave); median(fave)
# [1] 1.659
# [1] 1.65
altrestat()
 #
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 1.000 1.550 1.650 1.659 1.750 2.300
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
#
# Volendo posso costruire l'istogramma scegliendo gli intervalli. Battendo:
Istogramma(fave, 1,2.4, 0.2)
# (con la I maiuscola) ho l'istogramma a partire da 1 fino a 2.4 in classi ampie 0.2
#
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 1.000 1.550 1.650 1.659 1.750 2.300
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
#
# Volendo posso costruire l'istogramma scegliendo gli intervalli. Battendo:
Istogramma(fave, 1,2.4, 0.2)
# (con la I maiuscola) ho l'istogramma a partire da 1 fino a 2.4 in classi ampie 0.2
 # Un modo comodo (realizzabile anche senza computer) di organizzare i dati è l'uso di
# una specie di istrogramma a crocette col comando stem (in inglese "gambo"). Esempio:
stem(fave)
# The decimal point is 1 digit(s) to the left of the |
# 10 | 00
# 11 |
# 12 |
# 13 | 0055
# 14 | 000000000000000000000055
# 15 | 0000000000000000000000005555555555555555
# 16 | 0000000000000000000000000000000000000000005555555555555555555555
# 17 | 0000000000000000000000000000000000000000005555555555555555555555
# 18 | 00000000000000000000000000000055555555
# 19 | 000000000000000055
# 20 | 00
# 21 |
# 22 | 55
# 23 | 00
# La prima scritta ("The decimal …") dice che il punto decimale è una cifra a sinistra
# di |, ossia che 10|00, 11|, … stanno per 1.0, 1.1, … Ecco come rappresenterei i
# primi sei dati di "fave" (1.35,1.65,1.80,1.40,1.65,1.80) sulla carta quadrettata.
# Il computer mette in ordine le cifre a destra di |, ma non è importante farlo.
# Un modo comodo (realizzabile anche senza computer) di organizzare i dati è l'uso di
# una specie di istrogramma a crocette col comando stem (in inglese "gambo"). Esempio:
stem(fave)
# The decimal point is 1 digit(s) to the left of the |
# 10 | 00
# 11 |
# 12 |
# 13 | 0055
# 14 | 000000000000000000000055
# 15 | 0000000000000000000000005555555555555555
# 16 | 0000000000000000000000000000000000000000005555555555555555555555
# 17 | 0000000000000000000000000000000000000000005555555555555555555555
# 18 | 00000000000000000000000000000055555555
# 19 | 000000000000000055
# 20 | 00
# 21 |
# 22 | 55
# 23 | 00
# La prima scritta ("The decimal …") dice che il punto decimale è una cifra a sinistra
# di |, ossia che 10|00, 11|, … stanno per 1.0, 1.1, … Ecco come rappresenterei i
# primi sei dati di "fave" (1.35,1.65,1.80,1.40,1.65,1.80) sulla carta quadrettata.
# Il computer mette in ordine le cifre a destra di |, ma non è importante farlo.
 # Il nome "gambo" (stem) deriva dal fatto che i dati così presentati hanno la forma di
# foglie disposte lungo un gambo.
# Con l'opzione "width=0" posso ottenere la lunghezza delle colonne
stem(fave,width=0)
# The decimal point is 1 digit(s) to the left of the |
# 10 | +2
# 11 |
# 12 |
# 13 | +4
# 14 | +24
# 15 | +40
# 16 | +64
# 17 | +64
# 18 | +38
# 19 | +18
# 20 | +2
# 21 |
# 22 | +2
# 23 | +2
#
# Avessi già avuto i dati già ordinati
# 1, 1, 1.3, 1.3, 1.35, 1.35, 1.4, 1.4, 1.4, 1.4, 1.4, ...
# potevo evitare di batterli tutti ad uno ad uno usando il comando rep(x,n) che replica
# il dato x n volte:
FAVE <- c(rep(1,2), rep(1.3,2), rep(1.35,2), rep(1.4,22), rep(1.45,2), rep(1.5,24),
rep(1.55,16), rep(1.6,42), rep(1.65,22), rep(1.7,42), rep(1.75,22), rep(1.8,30),
rep(1.85,8), rep(1.9,16), rep(1.95,2), rep(2,2), rep(2.25,2), rep(2.3,2))
#
# Per studiare dati interi posso usare il comando Istogramma dandogli gli intervalli
# centrati sui valori interi da considerare. Vediamo ad es. come studiare i seguenti
# esiti del lancio di un dado costruito con del cartoncino nel modo illustrato sotto
# a sinistra:
dado <- c(
5,5,4,3,3,1,6,2,5,6,2,5,3,6,5,6,3,2,1,6,1,6,6,3,5,2,1,5,2,5,5,3,6,6,4,6,6,5,6,2,
1,6,6,3,2,2,5,6,3,2,6,6,6,4,2,3,6,6,6,2,6,4,5,4,6,2,3,5,6,6,2,2,1,5,5,3,5,3,5,6,
2,1,4,3,6,6,6,4,3,4,6,6,4,5,4,4,2,2,6,4,4,6,2,5,3,6,6,3,3,2,2,6,1,4,6,5,3,3,4,1,
6,4,6,6,2,5,5,1,5,2,6,5,2,2,4,1,2,2,6,1,6,5,5,6,1,3,3,4,5,5,5,6,4,4,6,3,6,3,6,6,
4,2,6,6,6,1,4,5,6,5,6,5,5,5,6,6,2,1,6,3,6,6,5,3,5,2,2,4,6,6,5,2,5,5,6,6,5,2,6,1)
# Il nome "gambo" (stem) deriva dal fatto che i dati così presentati hanno la forma di
# foglie disposte lungo un gambo.
# Con l'opzione "width=0" posso ottenere la lunghezza delle colonne
stem(fave,width=0)
# The decimal point is 1 digit(s) to the left of the |
# 10 | +2
# 11 |
# 12 |
# 13 | +4
# 14 | +24
# 15 | +40
# 16 | +64
# 17 | +64
# 18 | +38
# 19 | +18
# 20 | +2
# 21 |
# 22 | +2
# 23 | +2
#
# Avessi già avuto i dati già ordinati
# 1, 1, 1.3, 1.3, 1.35, 1.35, 1.4, 1.4, 1.4, 1.4, 1.4, ...
# potevo evitare di batterli tutti ad uno ad uno usando il comando rep(x,n) che replica
# il dato x n volte:
FAVE <- c(rep(1,2), rep(1.3,2), rep(1.35,2), rep(1.4,22), rep(1.45,2), rep(1.5,24),
rep(1.55,16), rep(1.6,42), rep(1.65,22), rep(1.7,42), rep(1.75,22), rep(1.8,30),
rep(1.85,8), rep(1.9,16), rep(1.95,2), rep(2,2), rep(2.25,2), rep(2.3,2))
#
# Per studiare dati interi posso usare il comando Istogramma dandogli gli intervalli
# centrati sui valori interi da considerare. Vediamo ad es. come studiare i seguenti
# esiti del lancio di un dado costruito con del cartoncino nel modo illustrato sotto
# a sinistra:
dado <- c(
5,5,4,3,3,1,6,2,5,6,2,5,3,6,5,6,3,2,1,6,1,6,6,3,5,2,1,5,2,5,5,3,6,6,4,6,6,5,6,2,
1,6,6,3,2,2,5,6,3,2,6,6,6,4,2,3,6,6,6,2,6,4,5,4,6,2,3,5,6,6,2,2,1,5,5,3,5,3,5,6,
2,1,4,3,6,6,6,4,3,4,6,6,4,5,4,4,2,2,6,4,4,6,2,5,3,6,6,3,3,2,2,6,1,4,6,5,3,3,4,1,
6,4,6,6,2,5,5,1,5,2,6,5,2,2,4,1,2,2,6,1,6,5,5,6,1,3,3,4,5,5,5,6,4,4,6,3,6,3,6,6,
4,2,6,6,6,1,4,5,6,5,6,5,5,5,6,6,2,1,6,3,6,6,5,3,5,2,2,4,6,6,5,2,5,5,6,6,5,2,6,1)

 # Il quadrato che contiene questo cerchio ha area 2·2 = 4
# Se il raggio è 2, 3, … area e semicirconferenza sono π·4, π·9, … e π·2, π·3, …
#
# Posso trasformare dei dati in modo proporzionale. Ad esempio posso trasformare degli
# angoli espressi in gradi in angoli espressi in centesimi di giro. Oppure posso vedere
# che percentuale di 160 è 250, cioè che cosa diventa 160 se esprimo il totale con 100
# invece che con 250. Oppure su che ora (tra 1, 2, …, 12) è posizionata lancetta che
# segna i 20 minuti.
# Il quadrato che contiene questo cerchio ha area 2·2 = 4
# Se il raggio è 2, 3, … area e semicirconferenza sono π·4, π·9, … e π·2, π·3, …
#
# Posso trasformare dei dati in modo proporzionale. Ad esempio posso trasformare degli
# angoli espressi in gradi in angoli espressi in centesimi di giro. Oppure posso vedere
# che percentuale di 160 è 250, cioè che cosa diventa 160 se esprimo il totale con 100
# invece che con 250. Oppure su che ora (tra 1, 2, …, 12) è posizionata lancetta che
# segna i 20 minuti.

 # Basta che usi (eventualmente dopo aver ingrandito la finestra grafica ad esempio con
# BF=6; HF=4) i comandi PERCENTUALI(tot), che associa 100 ad un certo totale tot, e
# RAPPORTI(tot1, tot2), che associa tot2 ad un certo totale tot1. Le immagini prece-
# denti sono delle fotografie di quello che si ottiene con:
PERCENTUALI(360)
PERCENTUALI(250)
RAPPORTI(60, 12)
# Man mano che passa 1 secondo il pallino blu sale di 1. Se vuoi cambiare la velocità
# puoi mettere davanti ad uno dei comandi precedenti il comando ATTESA=t con ad es.
# al posto di t 2 se vuoi che passino 2 secondi, 1/5 (o 0.2) se vuoi che passi 1/5 di
# secondo. Se vuoi che avere solo l'immgine relativa ad un certo valore di tot o tot1
# basta che fai precedere uno dei comandi precedenti da INPUT(dato) o OUTPUT(dato)
# (se vuoi interrompere prima l'animazione premi ESC). Esempi:
ATTESA=1/5; PERCENTUALI(360)
# Basta che usi (eventualmente dopo aver ingrandito la finestra grafica ad esempio con
# BF=6; HF=4) i comandi PERCENTUALI(tot), che associa 100 ad un certo totale tot, e
# RAPPORTI(tot1, tot2), che associa tot2 ad un certo totale tot1. Le immagini prece-
# denti sono delle fotografie di quello che si ottiene con:
PERCENTUALI(360)
PERCENTUALI(250)
RAPPORTI(60, 12)
# Man mano che passa 1 secondo il pallino blu sale di 1. Se vuoi cambiare la velocità
# puoi mettere davanti ad uno dei comandi precedenti il comando ATTESA=t con ad es.
# al posto di t 2 se vuoi che passino 2 secondi, 1/5 (o 0.2) se vuoi che passi 1/5 di
# secondo. Se vuoi che avere solo l'immgine relativa ad un certo valore di tot o tot1
# basta che fai precedere uno dei comandi precedenti da INPUT(dato) o OUTPUT(dato)
# (se vuoi interrompere prima l'animazione premi ESC). Esempi:
ATTESA=1/5; PERCENTUALI(360) # Non è altro che l'automazione dell'uso della carta millimetrata:
# Non è altro che l'automazione dell'uso della carta millimetrata:
 #
# (22)
# Delle funzioni numeriche ad 1 input ed 1 output possiamo fare i grafici.
#
# (22)
# Delle funzioni numeriche ad 1 input ed 1 output possiamo fare i grafici.
 # Ecco come ottenere il grafico della funzione che trasforma la temperatura in gradi
# centigradi (°C), in uso da noi, in quella in gradi Fahrenheit (°F), usati in
# Inghilterra e negli Stati Uniti.
# Uso il comando graficoF(g, a,b, col) che data una funzione g ne traccia automa-
# ticamente il grafico tra i numeri a e b nel colore col in un'opportuna Finestra.
#
Fa <- function(Ce) 32 + 72/40*Ce
graficoF(Fa, -35,105, "blue")
# Ecco come ottenere il grafico della funzione che trasforma la temperatura in gradi
# centigradi (°C), in uso da noi, in quella in gradi Fahrenheit (°F), usati in
# Inghilterra e negli Stati Uniti.
# Uso il comando graficoF(g, a,b, col) che data una funzione g ne traccia automa-
# ticamente il grafico tra i numeri a e b nel colore col in un'opportuna Finestra.
#
Fa <- function(Ce) 32 + 72/40*Ce
graficoF(Fa, -35,105, "blue")
 # Al centro che cosa si ottiene con qualche aggiunta:
scrivi(-10,225,"F")
scrivi(105,-15,"C")
segm(100,Fa(100), 0,Fa(100), 0); segm(100,Fa(100), 100,0, 0)
segm(0,Fa(0), 0,0, 0)
punto(0,Fa(0),"red"); punto(100,Fa(100),"red")
# I segmenti tratteggiati sono stati ottenuti mettendo come "colore" 0 (zero)
# Per colori diversi dei tratteggi (fig. sopra a destra) metto, ad es., coltrat="red".
#
# Se voglio mantenere la scala già scelta uso il comando grafico(g, a,b, col)
# Ecco i grafici delle funzioni x → x² e x → √x:
f1 <- function(x) x^2
f2 <- function(x) sqrt(x)
HF=3; BF=3
PIANO(-3,3,-1,5)
grafico(f1,-3,3, "brown")
grafico(f2,-3,3, "red") # tra -3 e 0 il grafico non viene tracciato
# Al centro che cosa si ottiene con qualche aggiunta:
scrivi(-10,225,"F")
scrivi(105,-15,"C")
segm(100,Fa(100), 0,Fa(100), 0); segm(100,Fa(100), 100,0, 0)
segm(0,Fa(0), 0,0, 0)
punto(0,Fa(0),"red"); punto(100,Fa(100),"red")
# I segmenti tratteggiati sono stati ottenuti mettendo come "colore" 0 (zero)
# Per colori diversi dei tratteggi (fig. sopra a destra) metto, ad es., coltrat="red".
#
# Se voglio mantenere la scala già scelta uso il comando grafico(g, a,b, col)
# Ecco i grafici delle funzioni x → x² e x → √x:
f1 <- function(x) x^2
f2 <- function(x) sqrt(x)
HF=3; BF=3
PIANO(-3,3,-1,5)
grafico(f1,-3,3, "brown")
grafico(f2,-3,3, "red") # tra -3 e 0 il grafico non viene tracciato
 # Il grafico tratteggiato è stato ottenuto mettendo come "colore" 0 (zero)
f3 <- function(x) x
grafico(f3,-3,3, 0)
#
# Il programma traccia automaticamente il grafico di una funzione per tantissimi punti.
# Posso farlo tracciare solo per un numero fissato di punti che metto in NpuntiF:
g = function(N) N*3
NpuntiF = 6; graficoF(g, 0,5, "brown")
# Il grafico tratteggiato è stato ottenuto mettendo come "colore" 0 (zero)
f3 <- function(x) x
grafico(f3,-3,3, 0)
#
# Il programma traccia automaticamente il grafico di una funzione per tantissimi punti.
# Posso farlo tracciare solo per un numero fissato di punti che metto in NpuntiF:
g = function(N) N*3
NpuntiF = 6; graficoF(g, 0,5, "brown")
 # Sopra al centro il grafico precedente sia per punti che continuo:
graficoF(g, -1,6, "yellow"); NpuntiF = 6; grafico(g, 0,5, "red")
# A destra con NPuntiF sono stati aggiunti cerchietti più grandi
NPuntiF = 6; grafico(g, 0,5, "black")
# Ecco sotto quello che ottengo usando NPUNTIF
# Sopra al centro il grafico precedente sia per punti che continuo:
graficoF(g, -1,6, "yellow"); NpuntiF = 6; grafico(g, 0,5, "red")
# A destra con NPuntiF sono stati aggiunti cerchietti più grandi
NPuntiF = 6; grafico(g, 0,5, "black")
# Ecco sotto quello che ottengo usando NPUNTIF
 NPUNTIF = 4; graficoF(g, -1,5, "blue"); NPUNTIF = 3; grafico(g, 0,4, "red")
# Oltre ai punti sono tracciati i segmenti verticali che li collegano all'asse x.
#
# Ecco come trovare i punti in cui il grafico di una funzione ha una gobba in su o in
# giù. Si usa il comando maxmin (o minmax) dando come input, oltre alla funzione,
# un intervallo che approssimi dove ciò accade:
V <- function(x) (x-1/3)^2-1
graficoF(V, -4,4, "red")
NPUNTIF = 4; graficoF(g, -1,5, "blue"); NPUNTIF = 3; grafico(g, 0,4, "red")
# Oltre ai punti sono tracciati i segmenti verticali che li collegano all'asse x.
#
# Ecco come trovare i punti in cui il grafico di una funzione ha una gobba in su o in
# giù. Si usa il comando maxmin (o minmax) dando come input, oltre alla funzione,
# un intervallo che approssimi dove ciò accade:
V <- function(x) (x-1/3)^2-1
graficoF(V, -4,4, "red")
 maxmin(V, -2,2)
# [1] 0.3333333
V( maxmin(V, -2,2) )
# [1] -1
punto(1/3,-1, "blue")
#
# Qui si può vedere come funzionano sia l'algoritmo per la ricerca dei massimi e dei
# minimi che quello per la soluzione delle equazioni.
#
# (23)
# Ecco come risolvere in modo approssimato una equazione che possiamo rappresentare
# graficamente mediante il grafico di una funzione.
# Riferiamoci all'esempio precedente e risolviamo rispetto ad x (x-1/3)^2-1 = 5, cioè
# V(x) = 5. Come sopra, basta che diamo in input, oltre alla funzione, un intervallo
# che approssimi la soluzione:
soluz(V, 5, 2,4)
# [1] 2.782823
maxmin(V, -2,2)
# [1] 0.3333333
V( maxmin(V, -2,2) )
# [1] -1
punto(1/3,-1, "blue")
#
# Qui si può vedere come funzionano sia l'algoritmo per la ricerca dei massimi e dei
# minimi che quello per la soluzione delle equazioni.
#
# (23)
# Ecco come risolvere in modo approssimato una equazione che possiamo rappresentare
# graficamente mediante il grafico di una funzione.
# Riferiamoci all'esempio precedente e risolviamo rispetto ad x (x-1/3)^2-1 = 5, cioè
# V(x) = 5. Come sopra, basta che diamo in input, oltre alla funzione, un intervallo
# che approssimi la soluzione:
soluz(V, 5, 2,4)
# [1] 2.782823
 # La soluzione è stata rappresentata graficamente con un pallino verde:
punto( 2.782823, V(2.782823), "green")
#
# In questo caso, abbastanza semplice, se si è in grado, si può risolvere l'equazione
# anche a mano:
# (x-1/3)^2-1 = 5
# porto -1 a destra cambiando segno (una sottrazione diventa una addizione):
# (x-1/3)^2 = 5+1
# faccio i calcoli:
# (x-1/3)^2 = 6
# la funzione inversa di "^2" è la radice quadrata:
# x-1/3 = √6
# porto -1/3 a destra:
# x = √6+1/3
# faccio i calcoli (con una calcolatrice o computer)
# x = 2.782823
#
# Se la soluzione dell'equazione corrisponde a un punto in cui il grafico raggiunge un
# massimo o un minimo, come nel caso seguente, per trovare la soluzione occorre usare
# il comando maxmin visto nel punto precedente.
# Soluzione dell'equazione 9*x^2-6*x = -1
# Se traccio il grafico di T con T(x) = 9*x^2-6*x (cerco x tale che T(x) = -1) ho:
# La soluzione è stata rappresentata graficamente con un pallino verde:
punto( 2.782823, V(2.782823), "green")
#
# In questo caso, abbastanza semplice, se si è in grado, si può risolvere l'equazione
# anche a mano:
# (x-1/3)^2-1 = 5
# porto -1 a destra cambiando segno (una sottrazione diventa una addizione):
# (x-1/3)^2 = 5+1
# faccio i calcoli:
# (x-1/3)^2 = 6
# la funzione inversa di "^2" è la radice quadrata:
# x-1/3 = √6
# porto -1/3 a destra:
# x = √6+1/3
# faccio i calcoli (con una calcolatrice o computer)
# x = 2.782823
#
# Se la soluzione dell'equazione corrisponde a un punto in cui il grafico raggiunge un
# massimo o un minimo, come nel caso seguente, per trovare la soluzione occorre usare
# il comando maxmin visto nel punto precedente.
# Soluzione dell'equazione 9*x^2-6*x = -1
# Se traccio il grafico di T con T(x) = 9*x^2-6*x (cerco x tale che T(x) = -1) ho:
 # Se provo a risolvere l'equazione con soluz (cerco la soluzione di T(x) = -1 tra
# -1 ed 1) ecco che cosa ottengo:
soluz(T,-1, -1,1)
# Error ... values at end points not of opposite sign
# Questo messaggio un po' strano ci dice che il grafico di T non scavalca la retta
# orizzontale y = -1. Posso trovare la soluzione cercando il minimo di T; verifico poi
# che qui T sia proprio -1.
maxmin(T, -1,1)
# [1] 0.3333333
T(1/3)
# [1] -1
# OK: la soluzione è 0.3333…, ossia 1/3.
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice:
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
# 06 Rivedere i comandi (^ v). function
# 07 Arrotondare numeri e risultati.
# 08 Le sequenze di numeri: seq :
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
punto_inclina (retta per p. con data incl.) poligono regolare poligo poligoC
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# 19 Diagrammi a torta, barre,striscia. CROSS. Goniometro. cartamm1, TERMOMETRO, …
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
# 23 Risolvere equazioni (soluz).
#
# Se provo a risolvere l'equazione con soluz (cerco la soluzione di T(x) = -1 tra
# -1 ed 1) ecco che cosa ottengo:
soluz(T,-1, -1,1)
# Error ... values at end points not of opposite sign
# Questo messaggio un po' strano ci dice che il grafico di T non scavalca la retta
# orizzontale y = -1. Posso trovare la soluzione cercando il minimo di T; verifico poi
# che qui T sia proprio -1.
maxmin(T, -1,1)
# [1] 0.3333333
T(1/3)
# [1] -1
# OK: la soluzione è 0.3333…, ossia 1/3.
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice:
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
# 06 Rivedere i comandi (^ v). function
# 07 Arrotondare numeri e risultati.
# 08 Le sequenze di numeri: seq :
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
punto_inclina (retta per p. con data incl.) poligono regolare poligo poligoC
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# 19 Diagrammi a torta, barre,striscia. CROSS. Goniometro. cartamm1, TERMOMETRO, …
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
# 23 Risolvere equazioni (soluz).
#