[ continuazione da qui, punto (20) ]
Per realizzare istogrammi di dati già classificati, non facili da tracciare con i
comandi standard, si può ricorrere al comando istoclas. Un esempio:
in Italia nel 1951 negli intervalli d'età [0,5),[5,10),[10,20),[20,30),[30,40),[40,50),
[50,60),[60,75),[75,100) sono morte 729,35,77,132,134,285,457,1401,1569 mila persone
(se gli estremi degli intervalli sono N le frequenze sono N-1)
#
interv <- c(0,5,10,20,30,40,50,60,75,100)
freq <- c(729,35,77,132,134,285,457,1401,1569)
istoclas(interv,freq)
# la media (pallino marrone) è circa 58.32019
# Per altre statistiche usa il comando altrestat()
altrestat()
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.00 43.43 66.00 58.32 80.80 100.00
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
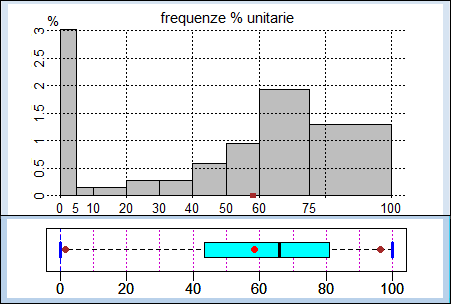 Sono state stimate, oltre alla media, alcuni percentili (il 25°, il 50° e il 75°,
o primo quartile, mediana e terzo quartile) ed è stato tracciato il box-plot.
[ per fare ciò si è generato un grande file di dati singoli distribuiti come
l'istogramma; il file è daticlas; volendo memorizzarlo per altri usi lo puoi
copiare in un file con altro nome; non devi visualizzarlo: sono 100 mila dati!
se vuoi avere un'idea di esso puoi battere str(daticlas) ]
Le frequenze percentuali unitarie sono le frequenze percentuali divise per la
ampiezza di ciascun intervallo, in modo che l'area di ogni rettangolo rappresenti
la frequenza relativa delle uscite che cadono nell'intervallo che ne è la base.
La somma delle aree dei rettangoli è 1, ossia 100%.
Per altri percentili usa percentile(n). Ad esempio per l'ampiezza del box
(differenza tra 75° e 25° percentile, distanza tra 1° e 3° quartile) batti:
percentile(75)-percentile(25)
# 37.3752
Sono state stimate, oltre alla media, alcuni percentili (il 25°, il 50° e il 75°,
o primo quartile, mediana e terzo quartile) ed è stato tracciato il box-plot.
[ per fare ciò si è generato un grande file di dati singoli distribuiti come
l'istogramma; il file è daticlas; volendo memorizzarlo per altri usi lo puoi
copiare in un file con altro nome; non devi visualizzarlo: sono 100 mila dati!
se vuoi avere un'idea di esso puoi battere str(daticlas) ]
Le frequenze percentuali unitarie sono le frequenze percentuali divise per la
ampiezza di ciascun intervallo, in modo che l'area di ogni rettangolo rappresenti
la frequenza relativa delle uscite che cadono nell'intervallo che ne è la base.
La somma delle aree dei rettangoli è 1, ossia 100%.
Per altri percentili usa percentile(n). Ad esempio per l'ampiezza del box
(differenza tra 75° e 25° percentile, distanza tra 1° e 3° quartile) batti:
percentile(75)-percentile(25)
# 37.3752
 Sono state stimate, oltre alla media, alcuni percentili (il 25°, il 50° e il 75°,
o primo quartile, mediana e terzo quartile) ed è stato tracciato il box-plot.
[ per fare ciò si è generato un grande file di dati singoli distribuiti come
l'istogramma; il file è daticlas; volendo memorizzarlo per altri usi lo puoi
copiare in un file con altro nome; non devi visualizzarlo: sono 100 mila dati!
se vuoi avere un'idea di esso puoi battere str(daticlas) ]
Le frequenze percentuali unitarie sono le frequenze percentuali divise per la
ampiezza di ciascun intervallo, in modo che l'area di ogni rettangolo rappresenti
la frequenza relativa delle uscite che cadono nell'intervallo che ne è la base.
La somma delle aree dei rettangoli è 1, ossia 100%.
Per altri percentili usa percentile(n). Ad esempio per l'ampiezza del box
(differenza tra 75° e 25° percentile, distanza tra 1° e 3° quartile) batti:
percentile(75)-percentile(25)
# 37.3752
Sono state stimate, oltre alla media, alcuni percentili (il 25°, il 50° e il 75°,
o primo quartile, mediana e terzo quartile) ed è stato tracciato il box-plot.
[ per fare ciò si è generato un grande file di dati singoli distribuiti come
l'istogramma; il file è daticlas; volendo memorizzarlo per altri usi lo puoi
copiare in un file con altro nome; non devi visualizzarlo: sono 100 mila dati!
se vuoi avere un'idea di esso puoi battere str(daticlas) ]
Le frequenze percentuali unitarie sono le frequenze percentuali divise per la
ampiezza di ciascun intervallo, in modo che l'area di ogni rettangolo rappresenti
la frequenza relativa delle uscite che cadono nell'intervallo che ne è la base.
La somma delle aree dei rettangoli è 1, ossia 100%.
Per altri percentili usa percentile(n). Ad esempio per l'ampiezza del box
(differenza tra 75° e 25° percentile, distanza tra 1° e 3° quartile) batti:
percentile(75)-percentile(25)
# 37.3752