---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
R. 1. Avvio all'uso (altro)
Premessa Uso come calcolatrice Altri calcoli Figure Grafici Statistica Altro
Questa guida è solo un'introduzione ai principali comandi, per prendere confidenza col
software e per illustrare alcune delle attività affrontabili con esso sin dalla scuola
di base (è utile agli insegnanti per preparare materiali e in alcuni casi per proporre
cose da far svolgere agli alunni, dopo che abbiano imparato a fare cose analoghe "a
mano"). In fondo vi è un indice.
# (A) All'avvio il programma presenta una riga che inizia con >. Dopo questo simbolo
# posso battere un "input", seguito dalla battitura di "a capo", e ottenere un eventuale
# "output", scritto in blu, preceduto da [1]. Con alcuni "comandi" posso avere più
# righe di output; in questi casi le successive righe sono precedute da [2],[3], ...
# Un semplice esempio:
> 10/4
# [1] 2.5
# Negli esempi che faremo non metteremo > in modo che i comandi si possano copiare da
# qui e mettere direttamente in R.
# Le parti che seguono # (come queste) sono per chi legge; sono copiabili in R ma non
# danno luogo ad alcuna esecuzione: in R i testi preceduti da # sono solo dei commenti.
# Puoi cambiare stile e dimensioni dei caratteri, ed altri aspetti (ad esempio per
# impiegare un proiettore): vedi.
# Per usare molti comandi (indicati dal punto (C) in poi) devi prima scrivere in R la
# riga seguente. Ti conviene copiarla e incollarla subito:
source("http://macosa.dima.unige.it/r.R")
USO come CALCOLATRICE
# (B) R può essere impiegato come una ottima calcolatrice; la divisione si indica /, la
# moltiplicazione *, un elevamento a potenza, come 6 alla 2, si indica con 6^2, dove ^
# indica che il 2 va pensato come se fosse sopraelevato.
6+2
# [1] 8
6-2; 2-6; 6*2; 6/2; 6^2
# [1] 4
# [1] -4
# [1] 12
# [1] 3
# [1] 36
# Come visto, posso eseguire più comandi separati da ; ottenendo uno sotto l'altro i
# risultati.
# I risultati possono avere molte o infinite cifre; ne sono visualizzate solo alcune:
5000/12
# [1] 416.6667
# 5000/12 fa 416.66666... ma il programma ne visualizza solo 7 cifre arrotondando la
# cifra finale 416.66666... -> 416.6667 (più vicino a 5000/12 di 416.6666)
# Osserva che appare 416.6667 e non 416,6667; analogamente per scrivere "1 e mezzo" si
# usa 1.5 invece di 1,5 (come si fa in genere a scuola in Italia).
# (C) Oltre a + * / ... con R puoi calcolare i valori di altre funzioni, che a input
# associano output. In genere gli input sono racchiusi tra parentesi. Alcuni esempi,
# round, sqrt o rad2, rad3:
round(5000/12, 3); round(5000/12, 1); round(5000/12, 0); round(5000/12, -2)
# [1] 416.667
# [1] 416.7
# [1] 417
# [1] 400
# Con round(5000/12, 3) arrotondo alla 3ª cifra dopo il ".". Con round(5000/12, 1) alla
# 1ª cifra. Con round(5000/12, 0) arrotondo agli interi. Con round(5000/12, -2) alle
# centinaia. Se ad esempio ho una spesa di 5000 euro da dividere tra 12 persone calcolo
# 5000/12 arrotondando il risultato ai centesimi, ossia alla 2ª cifra dopo il ".":
round(5000/12, 2)
# [1] 416.67
sqrt(4); sqrt(3); sqrt(3)^2
# [1] 2
# [1] 1.732051
# [1] 3
# sqrt sta per "square root", ossia "radice quadrata". Il lato di un quadrato che deve
# avere l'area di 3 m^2 dovrà essere di 1.73 m, cioè 173 cm.
# Invece di sqrt di può usare rad2. Per calcolare la radice cubica si può usare rad3.
# Il lato (in cm) di un cubo di volume 500 cm^3 (mezzo litro):
rad3(500)
# [1] 7.937005
# (D) Per calcoli di frazioni e per rappresentare sotto forma di frazioni numeri finiti
# o numeri periodici può essere utile ricorrere al comando frazio, o fraction. Esempi:
frazio(1.3333333333333); frazio(0.125); frazio(10/4); frazio(15/60+1/2)
# 4/3 1/8 5/2 3/4
# Per avere un rapporto in forma percentuale, ad es. 23/54 come 42.6% o 43%, faccio:
23/54*100; round(23/54*100,1); round(23/54*100,0)
# 42.59259 42.6 43
# Per scrivere numeri grossi o piccoli si può usare, come con la calcolatrice, la
# cosiddetta notazione esponenziale, usando ad es. e3 per intendere una moltiplicazione
# per 10^3 ed e-3 una divisone per 10^3, ossia una moltiplicazione per 10^-3.
# La stessa notazione la usa R per indicare numeri grossi e piccoli.
# Ecco alcuni modi di scrivere 100 mila e 2 decimi di millesimo:
100000; 100*1000; 100e3; 0.0002; 2e-4
# 1e+05 1e+05 1e+05 2e-04 2e-04
# Se devo calcolare 15+27 e dividere il risultato per il doppio della somma di 36 e 25,
# ossia calcolare quello che a volte a scuola viene scritto come (12+27)/[2*(36+25)],
# occorre stare attenti: le parentesi in matematica hanno significati diversi da quelli
# scolastici: le parentesi quadre, [ e ], e le parentesi graffe, { e }, vengono usate
# per indicare particolari oggetti matematici. Il software, e i matematici, scrivono
# un termine come il precedente come (12+27)/(2*(36+25)) usando solo parentesi tonde.
# Eventualmente ne cambiano le dimensioni: (12+27)/(2*(36+25)).
# Usando R è migliorabile la leggibilità aggiungendo degli spazi bianchi:
(12+27) / ( 2*(36+25) )
# [1] 0.3196721
# Infatti posso mettere tutti gli spazi che voglio tra parentesi, numeri e operazioni.
# (E) Ecco come eseguire la divisione con resto tra due numeri interi e come elencare
# i numeri interi positivi per cui è divisibile un numero intero (i suoi divisori).
div(13, 4)
# [1] 3 1
# 3 con resto 1; infatti 13 = 4*3 + 1
divisori(12) # o: divisors(12)
# [1] 1 2 3 4 6 12
Altri CALCOLI
# (F) In una formula come area = base*altezza (area del rettangolo) area, base e
# altezza sono delle variabili, ossia dei nomi a cui possono essere sostituiti dei
# valori. Anche in R posso usare le variabili. Devo stare attento alle dimensioni
# delle lettere: Base, BASE e base sono tre variabili differenti. Esempio:
base = 10; altezza = 5
base*altezza
# [1] 50
Base*altezza
# Errore: oggetto "Base" non trovato
# Potrei anche mettere il risultato di base*altezza in un'altra variabile e poi
# cercare il valore di essa:
area = base*altezza
area
# [1] 50
# (G) Se devo fare uno stesso calcolo riferito a più numeri, ad esempio 5, 10 e 3,
# posso mettere questi in una collezione di numeri, ossia metterli in c(5,10,3) e fare
# il calcolo con questo nuovo oggetto:
c(5,10,3)*2
# [1] 10 20 6
# Ci sono anche dei calcoli che si fanno specificamente sulle collezioni di oggetti; ad
# es. se voglio ordinare dei dati li metto come input della funzione sort (in inglese
# "sort" significa "ordinare") e ottengo come output i dati in ordine crescente:
sort( c(5,10,3) )
# [1] 3 5 10
# Posso estrarre un numero da una collezzione indicandone tra [ e ] il posto:
pippo = c(5,10,3); pippo[1]; pippo[2]
# [1] 5
# [1] 10
# Vediamo un esempio d'uso. Metto in altezze_alunni le altezze in cm di alcuni alunni
# di una classe (uso "_" per unire "altezze" e "alunni" in una sola variabile; ma
# potevo usare anche ad es. AltezzeAlunni). Poi li metto in ordine:
altezze_alunni = c(118, 135, 127, 119, 121, 124, 130, 132, 128, 122, 121, 123, 127)
sort(altezze_alunni)
# [1] 118 119 121 121 122 123 124 127 127 128 130 132 135
# Altri calcoli che posso fare (vediamo subito le uscite):
dati = altezze_alunni; min(dati); max(dati); length(dati); sum(dati)
# [1] 118
# [1] 135
# [1] 13
# [1] 1627
# Il significato dei comandi è evidente. Osservo solo che "length" e "sum" in inglese
# significano "lunghezza" (è la lunghezza della sequenza: 13 dati) e "somma".
# Ho copiato "altezze_alunni" in "dati" in modo da avere un nome più breve da scrivere.
# NOTA Se premo il tasto freccia in "su" [^] rivedo i precedenti comandi, con quello
# "giù" [v] i seguenti: cosa COMODA per richiamarli o modificarli. Prova ad usarli.
FIGURE
# (H) Vediamo alcuni comandi base per costruire figure geometriche.
# Procediamo per esempi.
PIANO(-1,10, -1,10)
# Si apre una finestra in cui appare la figura sopra a sinistra: una quadrettatura con
# indicati dei numeri che rappresentano, come in una cartina geografica, le coordinate
# dei vari punti. Appare anche, rosso ("red" in inglese), il punto che ha coordinata
# orizzontale 7 e come coordinata verticale 4. È stato tracciato col comando:
PUNTO(7,4, "red")
# Il punto più piccolo (in blu - "blue" in inglese) è stato ottenuto con:
Punto(2,4, "blue")
# Operando col mouse sulla barra del titolo della finestra grafica (vedi sotto) posso
# spostarla. Operando sui bordi od angoli posso ridimensionarla (vedi sopra a destra).
# Per cancellare una finestra che non mi serve ne clicco il bottone rosso X .
# Nuovi "piani" appaiono in finestre sovrappste. Per vedere i vecchi posso spostare le
# nuove finestre.
# La finestra inziale era larga e alta circa 3 dita. Se batto BF e HF (base e altezza,
# "height" in inglese) ottengo:
BF;HF
# [1] 3
# [1] 3
# Posso cambiare le dimensioni della finestra. Esempio:
BF=4; HF=2; PIANO(-50,50, 0,50)
# Se non cambio BF e HF le dimensioni rimangono queste. Le coordinate orizzontali
# vanno almeno da -50 a 50 e quelle verticali almeno da 0 a 50. Per tracciare le
# nuove finestre nelle dimensioni originali batto:
BF=3; HF=3
# Scrivo 4,2 per indicare il punto di coordinate 4 e 2. Con i comandi seguenti traccio
# il cerchio di centro 4,2 e raggio 3 nel colore blu e traccio in nero il centro. Poi
# traccio il cerchio passante per i 3 punti le cui prime coordinate metto in x e le
# seconde in y. Traccio il cerchio in rosso e i tre punti in nero. I nomi dei colori
# sono scritti in inglese. Al posto di "black" posso usare il numero 1.
PIANO(-1,10, -1,10)
cerchio(4,2, 3, "blue"); PUNTO(4,2,"black")
x = c(5, 8, 9); y = c(9, 3, 7.5)
cerchio3p(x,y, "red"); PUNTO(x,y, 1)
# È tracciato anche il centro del secondo cerchio, che, col raggio, ho ottenuto con:
centro3p; raggio3p
# [1] 6.076923 5.788462
# [1] 3.387291
PUNTO(6.076923, 5.788462, "orange")
# I nomi dei colori sono in inglese. Eccone alcuni [per vederne altri batti Colori()]:
# 1 black 2 grey 3 white 4 brown 5 orange 6 red 7 pink
# nero grigio bianco marrone arancione rosso rosa
# 8 magenta 9 blue 10 cyan 11 yellow 12 green 13 seagreen
# magenta blu ciano giallo verde verde mare
# (I) Vediamo qualche altra figura: segmenti, rette, ...
PIANO(0,10, 0,10)
# Traccio un po' di punti (figura a sinistra):
PUNTO(1,9,"blue"); PUNTO(4,9, "blue"); PUNTO(0,6,"brown"); PUNTO(4,8, "brown")
PUNTO(3,5,"magenta"); PUNTO(7,4, "magenta"); PUNTO(2,1, "red"); PUNTO(7,2,"red")
# e poi (a destra) due segmenti, una semiretta e una retta per due punti (queste ultime
# ovviamente sono tracciate solo in parte):
segm(1,9, 4,9, "blue"); segm(0,6, 4,8, "brown")
semiretta(3,5, 7,4, "magenta") # la semiretta che parte da 3,5 e passa per 7,4
retta2p(2,1, 7,2, "red") # la retta che passa per i 2 punti 2,1 e 7,2
# Vediamo qualche altra figura semplice:
PIANO(0,10, 0,10)
A = c(0,6); B = c(2,10); C = c(5,4)
PUNTO(A[1],A[2], "blue"); PUNTO(B[1],B[2], "blue"); PUNTO(C[1],C[2], "blue")
linea(A[1],A[2], B[1],B[2], "blue"); linea(A[1],A[2], C[1],C[2], "blue")
# Ho tracciato dei punti e dei segmenti sottili col comando linea (invece di segm)
# Ogni punto (A, B, C) l'ho memorizzato in una variabile, come collezione - vedi (G) -
# delle sue coordinate.
# Con punto_punto calcolo la distanza di A da B, con inclinazione l'inclinazione dei
# segmenti AB e AC. Con angolo posso misurare direttamente l'angolo CAB.
punto_punto(A[1],A[2], B[1],B[2])
# [1] 4.472136
inclinazione(A[1],A[2], B[1],B[2])
# [1] 63.43495
inclinazione(A[1],A[2], C[1],C[2])
# [1] -21.80141
angolo(C,A,B)
# [1] 85.23636
# Poi con medio2p ho tracciato il punto medio di AB
medio2p(A[1],A[2], B[1],B[2], "red")
# Nella figura a destra ho tracciato l'asse di AB, ossia la retta perpendicolare ad AB
# e passante per il suo punto medio.
asse2p(A[1],A[2], B[1],B[2], "red")
# (J) Vediamo come ottenere spezzate e poligoni. Il comando spezzata traccia la linea
# costituita dai segmenti che uniscono i punti con le coordinate indicate. Nell'esempio
# seguente il primo punto coincide con l'ultimo (in questo caso la spezzata è un
# poligono). lung ne calcola la lunghezza.
PIANO(-3,9,-2,10)
x = c(-3,2,8,8,-3); y = c(1,1,9,-1,1)
spezzata(x,y, "blue"); PUNTO(x,y, "red")
lung(x,y)
# [1] 36.18034
# Se voglio calcolare la lunghezza complessiva dei primi tre tratti, tra 1º e 4º punto:
lung(x[1:4],y[1:4])
# [1] 25
# Con spezzaC chiudo la spezzata tracciando colorato il poligono che essa delimita.
PIANO(-3,9,-2,10); spezzaC(x,y,"yellow")
# Al poligono giallo ho aggiunto un rettangolo rosso, ottenuto con:
A = c(0,2, 2,0, 0); B = c(4,4, 7,7, 4); spezzata(A,B, "red")
GRAFICI
# (K) Vediamo come realizzare il grafico di un fenomeno al variare di un altro. Con
# Piano (con la sola iniziale, "P", maiuscola) le "x" e le "y" sono rappresentate con
# scale che possono essere diverse
# Esempio: consumo medio di kg di frutta fresca all'anno da parte di un italiano.
anni = c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta = c(19, 21, 23, 28, 31, 27, 23, 37, 65, 88, 79)
# max è utile per scegliere il "Piano": trovo che il massimo è 88 e quindi faccio
# variare la y tra 0 e 90
max(frutta)
# [1] 88
BF=4; HF=2.5
Piano(1880,1980, 0,90)
spezzata(anni,frutta, "blue"); PUNTO(anni,frutta,"brown")
# Sono state messe anche delle scritte lungo gli assi con:
suassex("anni"); suassey("frutta")
# Posso fare il grafico anche di funzioni in cui "x" ed "y" sono legate da una formula.
# Es.: la trasformazione della temperatura in gradi centigradi (°C), in uso da noi, in
# quella in gradi Fahrenheit (°F), usati in Inghilterra e negli Stati Uniti.
Fa = function(Ce) 32 + 72/40*Ce
Fa(-30); Fa(110)
# -22 230
Piano(-30,110, -22,230)
grafico(Fa, -30,110, "brown")
suassey("°F"); suassex("°C")
PUNTO(100,Fa(100),"blue"); PUNTO(0,Fa(0),"blue")
# Ho ottenuto il grafico sopra a sinistra.
Fa(100)
# [1] 212
# Per trovare la temperatura in °F che corrisponde a 100°C ho semplicemente calcolato
# Fa(100). Per trovare qual è la temperatura k in °C che corrisponde a 100°F (vedi il
# grafico a destra) devo risolvere il problema "per quale k Fa(k)=100?". Potrei farlo
# "a mano". Oppure posso procedere usando il comando soluz nel modo seguente:
soluz(Fa,100, 20,60)
# [1] 37.77778
# Metto Fa,100 in quanto devo trovare la soluzione del problema:
# per quale input Fa vale 100?
# Metto 20,60 per indicare due valori tra cui sta la soluzione, ricavati dal grafico.
# 37.777… è dunque il valore di k.
# Posso procedere in modo analogo per ogni altro grafico.
# Il computer non fa altro che rendere veloce un procedimento che potrei fare diretta-
# mente io, via via con degli zoom per individuare con più precisione i gradi °C a cui
# corrispondono 100 °F:
STATISTICA
# (L) Le prime elaborazioni statistiche, affrontabili sin dai primi anni di scuola,
# sono gli istogrammi a crocette. Successivamente si può usare la carta quadrettata o
# millimetrata. Solo dopo ha senso usare il computer, per automatizzare procedimenti
# che si è imparato ad affrontare "a mano". Ecco qualche esempio.
# Gli abitanti (in migliaia) del Nord, del Centro e del Mezzogiorno:
# I comandi più semplici:
N = 25755; C = 12068; S = 20843; Italia = c(N,C,S)
Barre2(Italia); torta2(Italia); Striscia2(Italia)
# % 43.90107 20.57069 35.52824
nomi = c("N","C","S")
nomiBarre = nomi; Barre(Italia)
nomiTorta = nomi; torta(Italia)
nomiStriscia = nomi; Striscia(Italia)
# giallo,celeste,... % 43.90107 20.57069 35.52824
# giallo,celeste,... N C S
# Per ottenere la distribuzione percentuale arrotondata - vedi (C) - posso fare:
distribuzione(Italia, 0)
# 44 21 36
distribuzione(Italia, 2)
# 43.9 20.57 35.53 # se voglio poi scrivo 43.90 invece di 43.9
distribuzione(Italia, -1)
# 40 20 40
# (M) Questi erano dati già classificati. Vediamo come analizzare dati singoli.
# Osserviamo, come si vede nell'esempio seguente, che i comandi possono essere spezzati
# su più righe. Ecco le lunghezze di molte fave (ossia semi di fava) raccolte da una
# classe di alunni di 12 anni. Si devono copiare e incollare tutte le righe, da
# "fave = c(" fino alla riga finale ")".
fave = c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
# Abbiamo già visto in (G) come fare qualche prima analisi:
min(fave); max(fave); length(fave)
# 1 2.3 260
# Un modo comodo (realizzabile anche senza computer) di organizzare i dati è l'uso di
# una specie di istrogramma a crocette col comando stem (in inglese "gambo"). Esempio:
stem(fave)
# The decimal point is 1 digit(s) to the left of the |
# 10 | 00
# 11 |
# 12 |
# 13 | 0055
# 14 | 000000000000000000000055
# 15 | 0000000000000000000000005555555555555555
# 16 | 0000000000000000000000000000000000000000005555555555555555555555
# 17 | 0000000000000000000000000000000000000000005555555555555555555555
# 18 | 00000000000000000000000000000055555555
# 19 | 000000000000000055
# 20 | 00
# 21 |
# 22 | 55
# 23 | 00
# La prima scritta ("The decimal …") dice che il punto decimale è una cifra a sinistra
# di |, ossia che 10|00, 11|, … stanno per 1.0, 1.1, … Ecco come rappresenterei i
# primi sei dati di "fave" (1.35,1.65,1.80,1.40,1.65,1.80) sulla carta quadrettata.
# Il computer mette in ordine le cifre a destra di |, ma non è importante farlo.
# Il nome "gambo" (stem) deriva dal fatto che i dati così presentati hanno la forma di
# foglie disposte lungo un gambo.
# Posso comandare a stem, mettendo un numero minore o maggiore (come sotto) di 1, di
# classificare i dati in modo diverso:
stem(fave, 1.5)
# 10 | 00
# 10 |
# 11 |
# 11 |
# 12 |
# 12 |
# 13 | 00
# 13 | 55
# 14 | 0000000000000000000000
# 14 | 55
# 15 | 000000000000000000000000
# 15 | 5555555555555555
# 16 | 000000000000000000000000000000000000000000
# 16 | 5555555555555555555555
# 17 | 000000000000000000000000000000000000000000
# 17 | 5555555555555555555555
# 18 | 000000000000000000000000000000
# 18 | 55555555
# 19 | 0000000000000000
# 19 | 55
# 20 | 00
# 20 |
# 21 |
# 21 |
# 22 |
# 22 | 55
# 23 | 00
# Dopo aver imparato a fare semplici istogrammi a mano, si può usare il software:
isto(fave)
# [i lati della griglia distano il 5 %]
# Frequenze e frequenze percentuali:
# 2, 0,0, 4, 24, 40, 64, 64, 38, 18, 2,0,4
# 0.77,0,0,1.54,9.23,15.38,24.62,24.62,14.62,6.92,0.77,0,1.54
# Usando:
istogramma(beans)
# si ottiene anche la seguente frase, di cui vedremo tra poco i significato:
# Per altre statistiche usa il comando altrestat()
# Se le classi sono molte si può ottenere l'istogramma a destra, mettendo prima:
noClassi=1
# Come numero che indichi dove più o meno stanno i dati posso usare la mediana, che è
# il valore centrale dei dati; se i dati sono 5 prendo il 3º dato. Se i dati sono in
# quantità pari ci sono due valori al centro; in genere si prende il primo di essi. Nel
# nostro caso:
median(fave)
# [1] 1.65
# Potrei anche trovarlo ordinando i dati -vedi (G)-, che sono 260, e prendendo il 130º:
fave1 = sort(fave); fave1[130]
# [1] 1.65
# Un altro valore che si usa è la media, la somma dei dati divisa per la loro quantità:
sum(fave)/length(fave)
# [1] 1.659231
# Posso ottenerla anche col comando mean. Mi conviene poi arrotondarne il valore:
mean(fave); round( mean(fave),2 )
# [1] 1.659231
# [1] 1.66
# (N) Il comando isto/istogramma sceglie automaticamente gli intervalli in cui classifi-
# care i dati. In questo modo è facile costruire istogrammi anche nella scuola di base.
# Volendo posso costruire l'istogramma scegliendo gli intervalli. Battendo:
Isto(fave, 1,2.4, 0.2)
# (con la I maiuscola) ho l'istogramma a partire da 1 fino a 2.4 in classi ampie 0.2
# Con:
Istogramma(fave, 1,2.4, 0.2)
# come suggerito dalle uscite di "istogramma", ho anche:
# per altre statistiche usa il comando altrestat(). Facciamolo:
altrestat()
#
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 1.000 1.550 1.650 1.659 1.750 2.300
# I pallini sono il 5° e il 95° percentile
# Il pallino rosso è la media
# Le uscite di questo comando sono affrontabili solo alla fine della scuola media, ma
# possono essere assai utili ai docenti:
# minimo, 1° quartile (separazione tra il primo 25% dei dati e i successivi), mediana
# (o 2° quartile o 50° percentile), media, 3° quartile (o 75° percentile), massimo.
# Questo diagramma, dalla forma di una scatola ("box") con "baffi", è chiamato boxplot.
# Per inciso, non abbiamo parlato di moda. È un concetto non fondamentale e non facile
# da mettere a fuoco, in quanto dipende da come sono classificati di dati: è meglio
# non accennarlo nemmeno, nella scuola di base, e discuterne nelle superiori quando gli
# istogrammi saranno approssimati con curve continue. Nei casi come quelli presentati
# in (L) piuttosto che di moda si può parlare di "classe più frequente".
ALTRO
# (O) Vediamo qualche altro stumento, che può essere utile al docente.
# Dati tre numeri interi positivi come 90, 120 e 150 è facile trovarne il massimo
# comune divisore (MCD):
divisori(90); divisori(120); divisori(150)
# [1] 1 2 3 5 6 9 10 15 18 30 45 90
# [1] 1 2 3 4 5 6 8 10 12 15 20 24 30 40 60 120
# [1] 1 2 3 5 6 10 15 25 30 50 75 150
# Evidentemente è 30. Posso trovarlo anche con un comando specifico:
numeri = c(90,120,150); MCD(numeri)
# [1] 30
# Potrei usare anche il comando primi(N) che esprime N come prodotto di numeri "primi"
# (ossia numeri interi maggiori di 1 che sono multipli solo di 1 e di sé stessi):
primi(90); primi(120); primi(150)
# [1] 2 3 3 5
# [1] 2 2 2 3 5
# [1] 2 3 5 5
# Il massimo numero per cui sia 2*3*3*5 che 2*2*2*3*5 e 2*3*5*5 sono divisibili è:
2*3*5
# [1] 30
# Troviamo il minimo comune multiplo (MCM) degli stessi numeri:
MCM(numeri)
# [1] 1800
# Volendo potrei trovarlo prendendo ogni numero primo presente in primi(90), primi(120)
# o primi(150) con esponente pari al massimo numero di volte che compare in uno di essi:
2^3 * 3^2 * 5^2
# [1] 1800
# (P) Qualche strumento grafico.
# Puoi visualizzare l'ora con orologio();
# dopo 10 sec l'ora viene stampata.
orologio()
# [1] 09 15 32
# Con orologio2 puoi visualizzare l'ora che vuoi
orologio2(12,25,40) |  |
# Una torta "vuota" ed un goniometro (il goniometro è il cerchio diviso in gradi (°),
torta(0); gonio() # cioè in 360 parti uguali)
GONIO(0) # Un quarto di goniometro
Striscia(0) # Una striscia.
Con cartamm1() ho il foglio di carta
millimetrata riproddotto a fianco
(50 mm di base e 50 mm di altezza).
Con cartamm2() e cartamm3() ho quelli
di 100 mm di base e 50 mm di altezza e
di 100 mm di base e 100 mm di altezza
(altri posso ottenerli unendo queste
immagini; per altri ancora vedi il
documento successivo)
Per aggiungere degli assi posso usare:
segm(0,-50,0,50,"black"); segm(0,-50,0,50,"black")
o ad es. segm(-50,5, 50,5, "blue") se voglio che
l'asse x sia blu e passi sopra di 5 mm |  |
# Posso costruire una quadrettatura di m colonne e n righe col comando QUADRETTI(m,n)
# che la disegna in una nuova finestra:
BF=4.5; HF=1.5; QUADRETTI(15,5)
# con BF=3; HF=3; QUADRETTI(10,10) ho quadretti con lato di circa 5 mm.
#
# Eventualmente dopo aver ingrandito la finestra grafica (ad es. con BF=6; HF=4) con
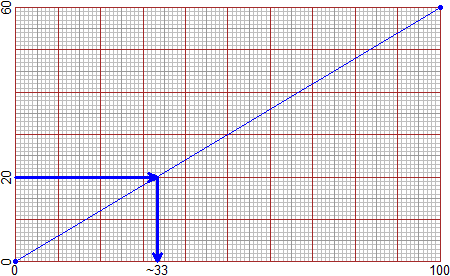
# RAPPORTI(tot1, tot2) puoi rappresentare la trasformazione proporzionale di dati
# associando tot2 ad un certo totale tot1. Fai precedere il comando da INPUT(dato) o
# OUTPUT(dato). Se poi usi rAPPORTI puoi rappresentare altri dati nella stessa finestra.
INPUT=20; RAPPORTI(60,12)
# Ottengo la figura a sinistra
INPUT=50; RAPPORTI(100,60)
INPUT=80; rAPPORTI(100,60); OUTPUT=20; rAPPORTI(100,60)
# Ottengo la figura a destra.
# Con RAPPORTI(100,tot) o RAPPORTI(tot,100) posso ottenere la rappresentazione grafica
# di percentuali. È uno strumento comodissimo per trasformare proporzionalmente dati.
# Non è altro che l'automazione dell'uso della carta millimetrata:
INDICE dei comandi
Premessa
> source("http://macosa.dima.unige.it/r.R")
Uso come calcolatrice
* / ; .
round sqrt rad2
rad3 frazio e
div divisori
Altri calcoli
= c(…) sort
[ ] min max
length sum
Figure
PIANO BF HF cerchio
PUNTO Punto cerchio3p centro3p
raggio3p Colori segm
segm semiretta retta2p
linea punto_punto inclinazione
angolo medio2p asse2p
spezzata lung […:…]
spezzaC
Grafici
Piano suassex suassey
function grafico soluz
Statistica
Barre torta Striscia
distribuzione min max
length stem isto(gramma)
noClassi median mean
Isto(gramma) altrestat
Altro
MCD primi MCM
orologio torta(0) gonio(0)
GONIO(0) Striscia(0) cartamm1/2/3
QUADRETTI INPUT OUTPUT
r/RAPPORTI
In Esempi d'uso di base trovi altri comandi (vedi le immagini per orientarti
nel documento). Molti altri li trovi in Altri esempi d'uso.
