---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
R. 3. Altri esempi d'uso (altro)
Clicca → QUI per il documento "Es. d'uso di base" del quale questo è un ampliamento.
Clicca → QUI per una versione aggiornata in lingua inglese.
Da 01 a 23 sono presentati ulteriori comandi ed esempi relativi alle parti con gli
stessi numeri di tale documento. Accedi ad esse cliccando il numero.
I numeri successivi sono parti nuove.
Per un indice di questo documento clicca QUI. In fondo c'è un indice alfabetico dei
comandi con l'indicazione di dove sono spiegati in questo e nel documento introduttivo.
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# Ricordiamo che dopo aver avviato R per eseguire vari comandi occorre copiare:
source("http://macosa.dima.unige.it/r.R")
# Per copiare qualche riga o comando già usato lo selezioni col mouse (premendo il
# pulsante sinstro) e azioni "copia/copy dal menu Modifica/Edit". Poi clicchi il punto
# dove vuoi copiarla e dallo stesso menu azioni "incolla/paste".
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
# Altri nomi di funzione (altri nel punto 07):
abs(3); abs(-2); sign(37); sign(-2.3); sign(0)
# 3 2 1 -1 0
rad2(x) rad3(x) rad4(x) rad5(x) sono le radici 2^,3^,4^,5^ di x
rad3(8); rad3(-8)
# 2 -2
# [ in matematica x^(1/3) è la radice cubica di x ma il software calcola x^(1/3) in un
# modo che funziona solo per x ≥ 0; rad3(x) allora calcola sign(x)*abs(x)^(1/3) ]
# INI_N(x) calcola la cifra decimale inziale del numero x
INI_N(0.25); INI_N(37*1000); INI_N(-57/10000000)
# 2 3 5
factorial(4); choose(10,3) # fattoriale, coeff. binomiale
# 24 (<- 4*3*2*1) 120 (<- 10/3*9/2*8/1)
M%/%N calcola il quoziente intero della divisione tra M e N, M%%N ne calcola il resto
750 %% 360; 750 %/% 360
# 30 2
# Per un help su altre funzioni meno elementari batti:
?Math
# Qualche esempio d'uso sulle funzioni circolari e sulle misure degli angoli
180*gradi; 180*gradi/pi; sin(30*gradi); cos(30*gradi); tan(45*gradi)
# 3.141593 1 0.5 0.8660254 1
cos(30*gradi); frazio(cos(30*gradi)/sqrt(3))
# 0.8660254 1/2 (capisco che cos(30°) = √3/2)
# Ma potrei usare anche WolframAlpha introducendo 0.8660254 e ottenendo √3/2
# o introducendo cos(30°) ottenendo √3/2
# ( "gradi" è definito come: gradi <- pi/180 )
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
# Uso prod per fare il prodotto di più numeri:
x <- c(2, 3, 7, 100); prod(x)
# 4200
# 06 Rivedere i comandi (^ v). function
# Se vuoi cancellare tulle le definizioni che hai introdotto puoi usare il comando
# rm(list=ls()). Devi però poi riazionare source("http://macosa.dima.unige.it/r.R")
# I messaggi di avviso sono inibiti: se batto 5/sqrt(-1)
# ottengo solo NaN (non è un numero)
# Per riattivarli devo introdurre options(warn=0). In tal caso ottengo anche:
# Warning message: In sqrt(-1) : Si è prodotto un NaN
# Per disattivarli nuovamente basta introdurre options(warn=-1)
# Di fronte ad una lunga sequenza di dati posso elencarne solo i primi per avere
# un'idea della loro "struttura" col comando str. Esempio:
str( divisori(123456) )
# num [1:28] 1 2 3 4 6 8 12 16 24 32 ... (sono 28 e iniziano con 1 2 3 4 6 ...)
# Posso usare str anche per esaminare la struttura di altri oggetti. Es.:
str(sin); str(choose)
# function (x) function (n,k) (sono funzioni la prima a 1 input, la seconda a 2)
# 07 Arrotondare numeri e risultati.
# Abbiamo visto come usare round. Vediamo altri comandi:
trunc(2.6); floor(2.6) # troncano invece che arrotondare ...
# 2 2
trunc(-7.4); floor(-7.4) # con differenze sui negativi (vedi)
# -7 -8
print(20/3, 2); print(20/3, 15) # arrot. a 2 e a 15 cifre; vedi, sotto, "piu"
# 6.7 6.66666666666667
signif(20/3, 2); signif(20/3, 7) # <- ovvero (cifre significative, al più 7)
# 6.7 6.666667
piu(11/13) visualizza più cifre (15) del valore tra parentesi, ultimo()
ha il valore dell'ultimo calcolo. Esempi:
(5/13+1/7)/17; frazio(ultimo()); piu((5/13+1/7)/17)
# 0.0310278 48/1547 0.0310277957336781
# Vediamo anche come si possono stampare tabelle di dati
# Ecco come stampare una sequenza di dati su più righe:
z <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4); length(z)
# 24 (i dati sono 24; li scrivo su 8 colonne separandoli con ", "
write(z, file="",sep=', ',ncolumns=8)
# 1, 2, 3, 4, 5, 6, 7, 8
# 9, 0, 1, 2, 3, 4, 5, 6
# 7, 8, 9, 0, 1, 2, 3, 4
write(z, file="",sep='\t',ncolumns=8) # li separo con il tabulatore
# 1 2 3 4 5 6 7 8
# 9 0 1 2 3 4 5 6
# 7 8 9 0 1 2 3 4
# (col comando write posso scrivere su file; in questi casi devo mettere file="")
# Col comando cat, che concatena le uscite, passando a nuove righe posso avere:
cat('',z[1:12],'\n',z[13:24],'\n')
# 1 2 3 4 5 6 7 8 9 0 1 2
# 3 4 5 6 7 8 9 0 1 2 3 4
# Se i dati hanno precisioni diverse le tabulazioni possono dar luogo a brutti effetti:
cat(20/3, 72, 15/4,'\n', 3, 1/9, 7,'\n')
# 6.666667 72 3.75
# 3 0.1111111 7
# Posso rimediare aggiungendo un tabulatore e arrotondando i dati, così:
k = function(x) round(x,3)
cat('',k(20/3),'\t',k(72),'\t',k(15/4),'\n',k(3),'\t',k(1/9),'\t',k(7),'\n')
# 6.667 72 3.75
# 3 0.111 7
# o, usando \b per introdurre un carattere di ritorno indietro (backspace):
cat('',k(20/3),'\t\b',k(72),'\t\b\b',k(15/4),'\n',k(3),'\t\b',k(1/9),'\t\b\b',k(7),'\n')
# 6.667 72 3.75
# 3 0.111 7
# o così:
k = function(x) signif(x,3)
cat('',k(20/3),'\t',k(72),'\t',k(15/4),'\n',k(3),'\t',k(1/9),'\t',k(7),'\n')
# 6.67 72 3.75
# 3 0.111 7
# o aggiungendo, in modo opportuno, più tabulatori:
cat('',20/3,'\t',72,'\t\t',15/4,'\n',3,'\t\t',1/9,'\t',7,'\n')
# 6.666667 72 3.75
# 3 0.1111111 7
# cat è comodo anche per stampare tabelle di vario tipo.
# Vediamo ad esempio la stampa di alcuni coefficienti binomiali:
# (si usa anche "for": vedi il punto 23 in fondo)
n <- 5; for(k in 0:n) cat("C(", n, ",", k, ") = ", choose(n,k), sep="", '\n')
# C(5,0) = 1
# C(5,1) = 5
# C(5,2) = 10
# C(5,3) = 10
# C(5,4) = 5
# C(5,5) = 1
# Vedi qui per il trangolo di Pascal
# 08 Le sequenze di numeri: seq :
# E' facile definire delle successioni per ricorsione. Facciamo due esempi.
# (si usano "for" e "while": vedi il punto 23 in fondo)
# Primo esempio. x(1)=1, x(n+1) = ( x(n) + A/x(n) ) / 2 (che converge a √A)
A=49/9; N=4; x <-1; for (i in 1:N) x <- (x+A/x)/2; x
# 2.333335
A=49/9; N=10; x <-1; for (i in 1:N) x <- (x+A/x)/2; x
# 2.333333
# Secondo esempio: u(1) = 1, u(2) = 2, u(n+2) = u( 3*u(n+1)-u(n) )
U1=1; U2=2; N=10; for(i in 3:N) {U=(3*U2-U1)/2; U1=U2; U2=U}; U
# 2.996094
U1=1; U2=2; N=20; for(i in 3:N) {U=(3*U2-U1)/2; U1=U2; U2=U}; U
# 2.999996
U1=1; U2=2; N=30; for(i in 3:N) {U=(3*U2-U1)/2; U1=U2; U2=U}; U
# 3
# Altro esempio, in cui non procedo per iterazione:
scambio = function(x,y) {q=x; x=y; y=q} # scambio tra loro x ed y
m=56; p=49; while(p>0){if(p>m) scambio(p,m); k=m; m=p; p=k%%p}; m
# (via via metto in ordine m,n e sostituisco m con m-n, n con il resto di m/n;
# ottengo il mass. com. divisore di m ed n)
# 7
m=4321; p=1234; while(p>0){if(p>m) scambio(p,m); scambio(p,m%%p)}; m
# 1
# Verifica usando il comando MCD:
MCD( c(56,49) ); MCD( c(4321,1234))
# 7 1
# Per un esempio di funzione definita per ricorsione più complessa vedi qui.
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico)
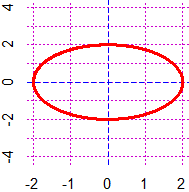
# Introducendo davanti a PIANO (o PIANOs …) RAPP = k posso cambiare il rapporto tra le
# scale; ad esempio se k = 2 (k = 1/2) i segmenti verticali (orizzontali) vengono
# "rappresentati" con lunghezza doppia (dimezzata) rispetto ai segmenti orizzontali
# "teoricamente" di eguale lunghezza.
RAPP = 1/2; PIANO(-2,2, -4,4)
cerchio(0,0, 2, "red")
 # 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# Si può rilavorare su un'immagine in un secondo tempo. Costruito un grafico o una
# figura in una finestra grafica, se batto Nome <- recordPlot() (Nome è un nome
# qualunque) l'immagine viene memorizzata. Se poi, dopo altre attività, apro una
# finestra e aziono replayPlot(Nome) viene visualizzata l'immagine iniziale, su cui
# posso continuare a lavorare. È utile anche per le animazioni (vedi 25).
# 13 punto punti Punti cerchio cerchio3p centro3p raggio3p
# Col comando arco(xCentro,yCentro, raggio, da,a, col) traccio archi di cerchio:
HF=2.5; BF=2.5; PIANO(-4,4, -4,4); cerchio(0,0, 4, "violet")
arco(-3,0, 1, 0,180, "blue"); arco(1,0, 3, 180,360, "red")
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# Si può rilavorare su un'immagine in un secondo tempo. Costruito un grafico o una
# figura in una finestra grafica, se batto Nome <- recordPlot() (Nome è un nome
# qualunque) l'immagine viene memorizzata. Se poi, dopo altre attività, apro una
# finestra e aziono replayPlot(Nome) viene visualizzata l'immagine iniziale, su cui
# posso continuare a lavorare. È utile anche per le animazioni (vedi 25).
# 13 punto punti Punti cerchio cerchio3p centro3p raggio3p
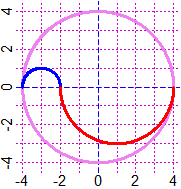
# Col comando arco(xCentro,yCentro, raggio, da,a, col) traccio archi di cerchio:
HF=2.5; BF=2.5; PIANO(-4,4, -4,4); cerchio(0,0, 4, "violet")
arco(-3,0, 1, 0,180, "blue"); arco(1,0, 3, 180,360, "red")
 # Un altro esempio: traccio un triangolo rettangolo ed evidenzio l'angolo retto.
PIANO(-1,10, -1,10)
segm(9,1, 3,8, "red"); inclinazione(9,1, 3,8)
# [1] -49.39871 (l'inclinazione del segmento rosso)
# Traccio da 3,8 nella direzione diminuita di 90° un segmento lungo 5
Direzione(3,8, inclinazione(9,1, 3,8)-90, 5, "blue")
# Traccio da x,y del punto di arrivo di Direzione il segm. fino a 9,1
segm(Direzionex,Direzioney, 9,1, "violet")
# Traccio l'arco centrato in 3,8 di raggio 2 che va da un lato all'altro
arco(3,8, 2, inclinazione(9,1, 3,8)-90, inclinazione(9,1, 3,8), "orange")
scrivi(3,5,"90°")
#
# cerch, cerch3p, arc fanno le stesse curve di cerchio, cerchio3p, arco ma sottili.
#
# P() consente di cliccare un punto e di leggerne le coordinate. La cosa è utile in
# tutti i casi in cui si ha che fare con grafici e immagini. Può essere utile anche
# per tracciare figure, un esempio:
HF=3; BF=3; PIANO(0,10, 0,10)
P() # clicco più o meno nel punto 5,9 e ottengo;
# xP <- ... ; yP <- ...
# poi riproduco ciascuna delle righe seguenti e clicco più o meno in 2,2 8,2 5,9
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "red")
# xP <- ... ; yP <- ... cose analoghe dopo le due righe seguenti
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
# Ottengo il triangolo rosso sotto a sinistra.
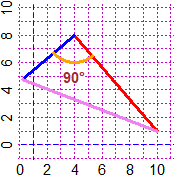
# Un altro esempio: traccio un triangolo rettangolo ed evidenzio l'angolo retto.
PIANO(-1,10, -1,10)
segm(9,1, 3,8, "red"); inclinazione(9,1, 3,8)
# [1] -49.39871 (l'inclinazione del segmento rosso)
# Traccio da 3,8 nella direzione diminuita di 90° un segmento lungo 5
Direzione(3,8, inclinazione(9,1, 3,8)-90, 5, "blue")
# Traccio da x,y del punto di arrivo di Direzione il segm. fino a 9,1
segm(Direzionex,Direzioney, 9,1, "violet")
# Traccio l'arco centrato in 3,8 di raggio 2 che va da un lato all'altro
arco(3,8, 2, inclinazione(9,1, 3,8)-90, inclinazione(9,1, 3,8), "orange")
scrivi(3,5,"90°")
#
# cerch, cerch3p, arc fanno le stesse curve di cerchio, cerchio3p, arco ma sottili.
#
# P() consente di cliccare un punto e di leggerne le coordinate. La cosa è utile in
# tutti i casi in cui si ha che fare con grafici e immagini. Può essere utile anche
# per tracciare figure, un esempio:
HF=3; BF=3; PIANO(0,10, 0,10)
P() # clicco più o meno nel punto 5,9 e ottengo;
# xP <- ... ; yP <- ...
# poi riproduco ciascuna delle righe seguenti e clicco più o meno in 2,2 8,2 5,9
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "red")
# xP <- ... ; yP <- ... cose analoghe dopo le due righe seguenti
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
# Ottengo il triangolo rosso sotto a sinistra.
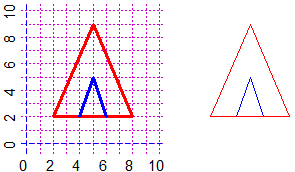 # In modo analogo traccio la figura blu:
P()
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
# Poi, se voglio riprodurre la figura senza scala posso usare i valori x,y via via
# stampati, ottenendo la figura a destra (se usassi "spezzata" avrei le linee spesse)
PIANOss(0,10, 0,10)
x <- c(2,8,5,2); y <- c(2,2,9,2); spezza(x,y, "red")
x <- c(6,5,4); y <- c(2,5,2); spezza(x,y, "blue")
# 14 xy(n): le coordinate del punto che clicco. I colori.
# Puoi usare, oltre a 1 (nero), i successivi numeri interi per indicare alcuni colori (8):
HF=1; BF=4; PIANO(0,21,-1,1); for (c in 1:20) PUNTO(c,0, c)
# La cosa può essere comoda in alcuni casi
# In modo analogo traccio la figura blu:
P()
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
# Poi, se voglio riprodurre la figura senza scala posso usare i valori x,y via via
# stampati, ottenendo la figura a destra (se usassi "spezzata" avrei le linee spesse)
PIANOss(0,10, 0,10)
x <- c(2,8,5,2); y <- c(2,2,9,2); spezza(x,y, "red")
x <- c(6,5,4); y <- c(2,5,2); spezza(x,y, "blue")
# 14 xy(n): le coordinate del punto che clicco. I colori.
# Puoi usare, oltre a 1 (nero), i successivi numeri interi per indicare alcuni colori (8):
HF=1; BF=4; PIANO(0,21,-1,1); for (c in 1:20) PUNTO(c,0, c)
# La cosa può essere comoda in alcuni casi
 # Col comando Ncolori() posso richiamare i numeri associati ai colori:
Ncolori()
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet, 7 yellow, 8 grey
# Più in generale puoi specificare i colori indicandoli con rgb(a,b,c) con a,b,c numeri
# tra 0 ed 1 che indicano la quantità di rosso (red), verde (green) e blu (blue) che li
# formano: PUNTO(2,3, rgb(1,0,0) ) fa il punto (2,3) rosso, PUNTO(4,5, rgb(1,0.5,0) )
# fa (4,5) arancione, PUNTO(3,2, rgb(0.7,0.7,0.7) ) fa (3,2) grigio
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# Per altri modi di realizzare un piano senza griglie vedi il punto 25
# semir, r2p e a2p funzionano come semiretta, retta2p e asse2p ma usano tratti sottili.
# cartamm consente di realizzare carta millimetrata. Volendo posso tracciarvi grafici o
# (usando rect, con le coordinate di vertici opposti - in col metto il colore interno,
# in border potrei mettere quello del bordo) istogrammi:
cartamm(40,25); x <- c(1,23,38); y <- c(23,9,17); spezzata(x,y,"red")
cartamm(40,25)
rect(5,0, 10,17, col="red"); rect(10,0, 15,22, col="green")
rect(15,0, 20,9, col="blue"); rect(20,0, 25,15, col="cyan")
rect(25,0, 30,19,col="violet"); rect(30,0, 35,12, col="yellow")
# Col comando Ncolori() posso richiamare i numeri associati ai colori:
Ncolori()
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet, 7 yellow, 8 grey
# Più in generale puoi specificare i colori indicandoli con rgb(a,b,c) con a,b,c numeri
# tra 0 ed 1 che indicano la quantità di rosso (red), verde (green) e blu (blue) che li
# formano: PUNTO(2,3, rgb(1,0,0) ) fa il punto (2,3) rosso, PUNTO(4,5, rgb(1,0.5,0) )
# fa (4,5) arancione, PUNTO(3,2, rgb(0.7,0.7,0.7) ) fa (3,2) grigio
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# Per altri modi di realizzare un piano senza griglie vedi il punto 25
# semir, r2p e a2p funzionano come semiretta, retta2p e asse2p ma usano tratti sottili.
# cartamm consente di realizzare carta millimetrata. Volendo posso tracciarvi grafici o
# (usando rect, con le coordinate di vertici opposti - in col metto il colore interno,
# in border potrei mettere quello del bordo) istogrammi:
cartamm(40,25); x <- c(1,23,38); y <- c(23,9,17); spezzata(x,y,"red")
cartamm(40,25)
rect(5,0, 10,17, col="red"); rect(10,0, 15,22, col="green")
rect(15,0, 20,9, col="blue"); rect(20,0, 25,15, col="cyan")
rect(25,0, 30,19,col="violet"); rect(30,0, 35,12, col="yellow")
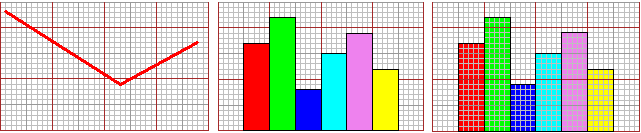 # Cartamm ritraccia la carta mm sullo stesso schermo. La figura sopra a destra è stata
# ottenuta con Cartamm(40,25) (e ritracciando i rettangoli senza col=...).
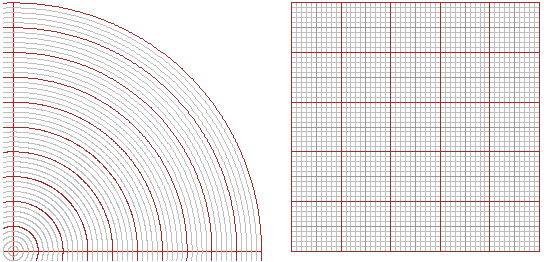
# Se nel comando cartamm dò come input (50,50) l'immagine viene prodotta in dimensioni
# fissate, circa 50 mm × 50 mm. Posso rappresentare nella stessa scala cerchi come
# quelli sottostanti. Per dettagli vedi qui (le immagini seguenti sono ridotte).
# (vedi anche cartamm1(),...,cartamm3() discussi al punto 19 del documento precedente)
# Cartamm ritraccia la carta mm sullo stesso schermo. La figura sopra a destra è stata
# ottenuta con Cartamm(40,25) (e ritracciando i rettangoli senza col=...).
# Se nel comando cartamm dò come input (50,50) l'immagine viene prodotta in dimensioni
# fissate, circa 50 mm × 50 mm. Posso rappresentare nella stessa scala cerchi come
# quelli sottostanti. Per dettagli vedi qui (le immagini seguenti sono ridotte).
# (vedi anche cartamm1(),...,cartamm3() discussi al punto 19 del documento precedente)
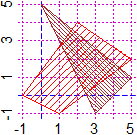
 # 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
# Direzione punto_punto punto_retta retta_retta punto_incl poligono
# spezzaL, spezza2L operano come spezzaC evidenziando il poligono con
# linee (± fitte) con inclinazione data in input invece che con un colore
PIANO(-1,5, -1,5)
x <- c(-1,1,5,2); y <- c(0,-1,2,4); spezzaL(x,y, 45, "red")
x1 <- c(0,3,5); y1 <- c(5,-1,1); spezza2L(x1,y1, -45, "brown")
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
# Direzione punto_punto punto_retta retta_retta punto_incl poligono
# spezzaL, spezza2L operano come spezzaC evidenziando il poligono con
# linee (± fitte) con inclinazione data in input invece che con un colore
PIANO(-1,5, -1,5)
x <- c(-1,1,5,2); y <- c(0,-1,2,4); spezzaL(x,y, 45, "red")
x1 <- c(0,3,5); y1 <- c(5,-1,1); spezza2L(x1,y1, -45, "brown")
 | 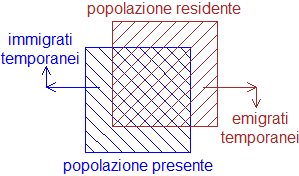 |
# Col comando text posso mettere scritte più sofisticate di quelle realizzabili col
# comando scrivi. Posso colorarle, farle in grassetto o corsivo, dimensionarle: con
# text(x,y,testo, font=N) le ho in grassetto se N è 2, corsivo se 3, grassetto/corsivo
# se 4. text(…, cex=…) con in … un num. >1 / <1 (ad es. 0.8 e 1.2) ho scritte più
# grosse/piccole. Se metto \n (nuova riga) viene inserito un a capo.
# Volendo posso allineare a sinistra o destra di x,y con text(…,adj=0) o text(…,adj=1)
# Posso inclinare le scritte: text(…, srt=-90), text(…, srt=45) ("srt" sta per "string
# rotation") ruotano la scritta di -90° o di 45° rispetto alla direzione dell'asse x
BF=4;HF=4; PIANOss(-2.7,2.7, -2.7,2.7)
# (prima mi conviene usare PIANO per vedere la griglia e poi ricopiare con PIANOss)
x <- c(-1,1,1,-1); y <- c(-1,-1,1,1)
spezzaL(x-1/4,y-1/4, -45, "blue"); spezzaL(x+1/4,y+1/4, 45, "brown")
text( 0.25, 1.5, "popolazione residente", col="brown")
text(-0.25,-1.5, "popolazione presente", col="blue")
frec(1,0,2,0,"brown"); frec2(2,-0.4,"brown")
text(2.1,-0.75, "emigrati\ntemporanei", col="brown")
frec(-1,0,-2,0,"blue"); frec2(-2,0.4,"blue")
text(-2.1,0.75, "immigrati\ntemporanei", col="blue")
# frec2 e freccia2 congiungono la punta dell'ultima freccia con la nuova
# Lo stesso vale per Frec2 e Freccia2; le frecce blu in nero:
Frec(-1,0,-180,1,"black"); Frec2(90,0.4,"black")
#
# Comunque \n posso usarlo anche con scrivi. Sia con scrivi che con text posso usare
# ad esempio bquote(2*pi) e bquote(sqrt(3)) come scritte per 2π e √3.
# Per altre simboli e formule ottenibili con bquote vedi qui. Esempi:
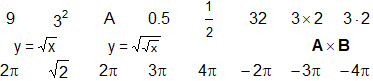 #
# Se nel comando già visto Direzione(x,y, d,r, colore) si sceglie 0 come colore il
# "raggio" lungo r da x,y nella direzione d non viene tracciato. Ciò consente di avere
# comunque in Direzionex e Direzioney le coordinate del punto di arrivo. Un esempio:
# (vedi qui per i comandi)
#
# Se nel comando già visto Direzione(x,y, d,r, colore) si sceglie 0 come colore il
# "raggio" lungo r da x,y nella direzione d non viene tracciato. Ciò consente di avere
# comunque in Direzionex e Direzioney le coordinate del punto di arrivo. Un esempio:
# (vedi qui per i comandi)
 # Altri comandi utili per tracciare figure.
# Per traslare, ruotare, moltiplicare le coordinate dei punti posso usare i comandi:
# MolTraRot(x,y, mx,my, tx,ty, ang) e RotTraMol(x,y, ang, tx,ty, mx,my). Dato (x,y) il
# primo ne moltiplica le coordinate per mx ed my, poi lo trasla di tx,ty e infine lo
# ruota attorno a (0,0) di ang. Il secondo invece prima lo ruota attorno a (0,0), poi
# lo trasla e infine ne moltiplica le coordinate. Se aggiungo al comando [1] o [2] ho
# la 1ª o la 2ª coordinata. Per operare su curve vedi 27.
# Vedi qui per un esempio, che genera la figura seguente.
# Altri comandi utili per tracciare figure.
# Per traslare, ruotare, moltiplicare le coordinate dei punti posso usare i comandi:
# MolTraRot(x,y, mx,my, tx,ty, ang) e RotTraMol(x,y, ang, tx,ty, mx,my). Dato (x,y) il
# primo ne moltiplica le coordinate per mx ed my, poi lo trasla di tx,ty e infine lo
# ruota attorno a (0,0) di ang. Il secondo invece prima lo ruota attorno a (0,0), poi
# lo trasla e infine ne moltiplica le coordinate. Se aggiungo al comando [1] o [2] ho
# la 1ª o la 2ª coordinata. Per operare su curve vedi 27.
# Vedi qui per un esempio, che genera la figura seguente.
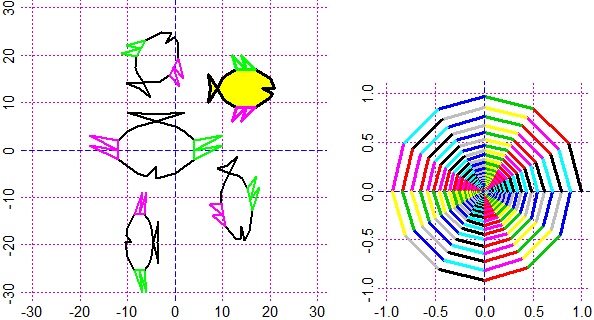 # Tracciato un segmento o una freccia (con i comandi freccia, segm, linea, ...) le
# coordinate del punto finale sono memorizzate in xpunta e ypunta. La cosa può essere
# utile per costruire vari tipi di figure. Un punto inziale può essere tracciato con
# punticino: le sue coordinate sono messe in xpunta, ypunta. Vedi qui per un esempio,
# che genera la figura sopra a destra.
# punticino2 traccia invece un punto leggeremente più grande (3 pixel di diametro).
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
# Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
# Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# Se voglio mettere una scritta S su una parte con sfondo nel colore COLOR posso usare
# scriviC(x,y, COLOR, S) invece di scrivi(x,y, S)
# Per inserire un "a capo" posso inserire \n in S (vedi 16).
# Posso scrivere scritte ruotate col comando scriviR(x,y, Angolo, S) con Angolo in
# gradi e scritte ruotate e su sfondo colorato con scriviRC(x,y, Angolo, COLOR, S)
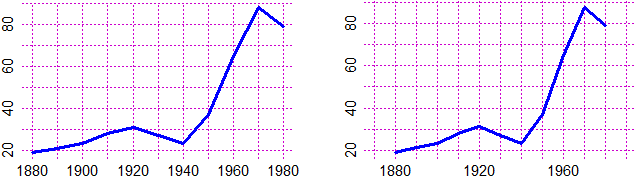
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# sottoassex(scritta), sottoassey(scritta) operano come suassex, suassey
# suAssex(scritta,x), suAssey(scritta,y), sottoAssex(…), sottoAssey(…)
# consentono di scegliere le coordinate in cui mettere le scritte
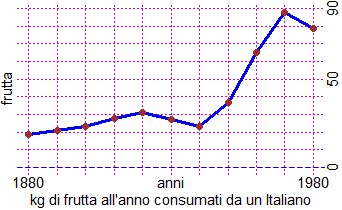
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
BF=4; HF=2.5
Griglia(1880,1980, 0,90) # Per Griglia vedi (15) di "es. uso di base":
# fa la griglia senza scritte lungo gli assi
spezzata(anni,frutta, "blue"); PUNTI(anni,frutta,"brown")
sottoassex("anni"); sottoassey("frutta")
sottoAssex("1880", 1880); sottoAssex("1980", 1980)
suAssey("90",90); suAssey("0",0); suAssey("50",50)
# Se la scritta invece che "frutta" è "90" posso fare a mano di mettere le virgolette:
# invece di suAssey("90",90) potrei mettere suAssey(90,90) o anche suAssey(9*10,90)
# Tracciato un segmento o una freccia (con i comandi freccia, segm, linea, ...) le
# coordinate del punto finale sono memorizzate in xpunta e ypunta. La cosa può essere
# utile per costruire vari tipi di figure. Un punto inziale può essere tracciato con
# punticino: le sue coordinate sono messe in xpunta, ypunta. Vedi qui per un esempio,
# che genera la figura sopra a destra.
# punticino2 traccia invece un punto leggeremente più grande (3 pixel di diametro).
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
# Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
# Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# Se voglio mettere una scritta S su una parte con sfondo nel colore COLOR posso usare
# scriviC(x,y, COLOR, S) invece di scrivi(x,y, S)
# Per inserire un "a capo" posso inserire \n in S (vedi 16).
# Posso scrivere scritte ruotate col comando scriviR(x,y, Angolo, S) con Angolo in
# gradi e scritte ruotate e su sfondo colorato con scriviRC(x,y, Angolo, COLOR, S)
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# sottoassex(scritta), sottoassey(scritta) operano come suassex, suassey
# suAssex(scritta,x), suAssey(scritta,y), sottoAssex(…), sottoAssey(…)
# consentono di scegliere le coordinate in cui mettere le scritte
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
BF=4; HF=2.5
Griglia(1880,1980, 0,90) # Per Griglia vedi (15) di "es. uso di base":
# fa la griglia senza scritte lungo gli assi
spezzata(anni,frutta, "blue"); PUNTI(anni,frutta,"brown")
sottoassex("anni"); sottoassey("frutta")
sottoAssex("1880", 1880); sottoAssex("1980", 1980)
suAssey("90",90); suAssey("0",0); suAssey("50",50)
# Se la scritta invece che "frutta" è "90" posso fare a mano di mettere le virgolette:
# invece di suAssey("90",90) potrei mettere suAssey(90,90) o anche suAssey(9*10,90)
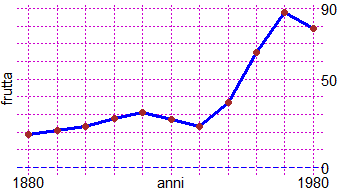
 sottoassex2 scrive in una riga sottostante a quella usata da "sottoassex":
sottoassex2("kg di frutta all'anno consumati da un Italiano")
# Con la S maiuscola SuAssey e SottoAssey scrivono i numeri orizzontali.
n=c(90,0,50); for(i in 1:3) SuAssey(n[i],n[i])
sottoassex2 scrive in una riga sottostante a quella usata da "sottoassex":
sottoassex2("kg di frutta all'anno consumati da un Italiano")
# Con la S maiuscola SuAssey e SottoAssey scrivono i numeri orizzontali.
n=c(90,0,50); for(i in 1:3) SuAssey(n[i],n[i])
 # Il comando PianoP(x,y), dati dei punti con ascisse x e ordinate y, sceglie automatica-
# mente un "piano" che li contenga (è qualcosa di analogo a graficoF per le funzioni);
# PIANOP(x,y) lo sceglie monometrico. La cosa può essere comoda in molte situazioni.
# Vediamolo, per brevità, in questa:
PianoP(anni,frutta); spezzata(anni,frutta, "blue")
PIANOP(anni,frutta); spezzata(anni,frutta, "blue")
# Il comando PianoP(x,y), dati dei punti con ascisse x e ordinate y, sceglie automatica-
# mente un "piano" che li contenga (è qualcosa di analogo a graficoF per le funzioni);
# PIANOP(x,y) lo sceglie monometrico. La cosa può essere comoda in molte situazioni.
# Vediamolo, per brevità, in questa:
PianoP(anni,frutta); spezzata(anni,frutta, "blue")
PIANOP(anni,frutta); spezzata(anni,frutta, "blue")
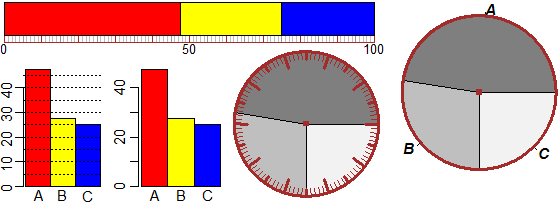
 # 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm, TERMOMETRO
# Mentre torta, Torta, Tortam, Barre, Striscia scelgono automaticamente i colori
# con tortaC, TortaC, TortaM, StrisciaC, BarreC puoi aggiungere i colori.
da<- c(237.5,137.5,125); co<- c("red","yellow","blue")
nomiStriscia = c("A","B","C"); StrisciaC(da,co)
nomiBarre = c("A","B","C"); BarreC(da,co)
tortaC( da, c("grey50", "grey75", "grey95"))
# % 47.5 27.5 25
# 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm, TERMOMETRO
# Mentre torta, Torta, Tortam, Barre, Striscia scelgono automaticamente i colori
# con tortaC, TortaC, TortaM, StrisciaC, BarreC puoi aggiungere i colori.
da<- c(237.5,137.5,125); co<- c("red","yellow","blue")
nomiStriscia = c("A","B","C"); StrisciaC(da,co)
nomiBarre = c("A","B","C"); BarreC(da,co)
tortaC( da, c("grey50", "grey75", "grey95"))
# % 47.5 27.5 25
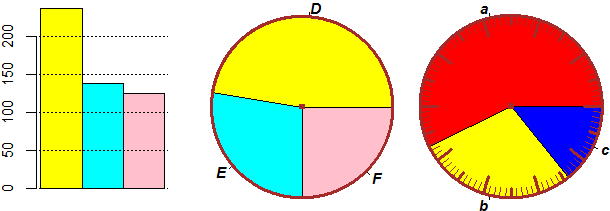
 # Il 2° diagramma a barre è stato ottenuto premettendo noGrglia=1.
# L'areogramma circolare a destra, in cui sono state aggiunte automaticamente delle
# lettere ai vari settori è stato ottenuto con Torta2C. Aggiungono automaticamente
# delle lettere anche torta2C, Torta2, torta2.
# Se nel grafico a barre voglio rappresentare i dati invece che le percentuali uso:
nomiBarre = c("A","B","C"); BARREC(da,co)
# ovvero (vedi l'uscita sotto a sinistra):
BARRE(da)
# giallo,celeste,... 237.5 137.5 125
# giallo,celeste,... % 47.5 27.5 25
# Il 2° diagramma a barre è stato ottenuto premettendo noGrglia=1.
# L'areogramma circolare a destra, in cui sono state aggiunte automaticamente delle
# lettere ai vari settori è stato ottenuto con Torta2C. Aggiungono automaticamente
# delle lettere anche torta2C, Torta2, torta2.
# Se nel grafico a barre voglio rappresentare i dati invece che le percentuali uso:
nomiBarre = c("A","B","C"); BARREC(da,co)
# ovvero (vedi l'uscita sotto a sinistra):
BARRE(da)
# giallo,celeste,... 237.5 137.5 125
# giallo,celeste,... % 47.5 27.5 25
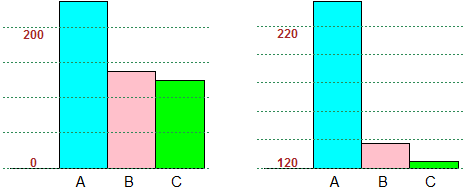
 # Agli areogrammi circolari per semplicità i nomi sono assegnati automaticamente. Se
# devo distinguere vari areogrammi posso dar loro nomi diversi coi comandi Torta_C,
# torta_C, Torta_, torta_, analoghi ai comandi con 2 al posto di _, a cui aggiungo,
# dopo una virgola, un numero che indica il nome del primo settore: le lettere A,B,…,Z
# sono indicate dai numeri 1,2,…,26, le lettere a,b,…,z dai numeri 27,28,…,52.
da2 <- c(100,50,25); Torta_(da, 4); torta_C(da2,co, 27)
# % 47.5 27.5 25 % 57.14286 28.57143 14.28571
# Nota: È totalmente senza senso (anche se è usato da chi vuole ingannare il lettore)
# utilizzare areogrammi a settori circolari a forma di disco inclinato. Vedi qui.
# Usando BARRE2 è posso realizzare diagrammi a barre che non partono da 0: vedi qui.
# Agli areogrammi circolari per semplicità i nomi sono assegnati automaticamente. Se
# devo distinguere vari areogrammi posso dar loro nomi diversi coi comandi Torta_C,
# torta_C, Torta_, torta_, analoghi ai comandi con 2 al posto di _, a cui aggiungo,
# dopo una virgola, un numero che indica il nome del primo settore: le lettere A,B,…,Z
# sono indicate dai numeri 1,2,…,26, le lettere a,b,…,z dai numeri 27,28,…,52.
da2 <- c(100,50,25); Torta_(da, 4); torta_C(da2,co, 27)
# % 47.5 27.5 25 % 57.14286 28.57143 14.28571
# Nota: È totalmente senza senso (anche se è usato da chi vuole ingannare il lettore)
# utilizzare areogrammi a settori circolari a forma di disco inclinato. Vedi qui.
# Usando BARRE2 è posso realizzare diagrammi a barre che non partono da 0: vedi qui.
 # 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# Per avere altri percentili, dopo aver battuto altrestat(), puoi usare, ad es. per il
# 3° percentile, quantile(daticlas, 3/100). Con quantile(daticlas,1/2) hai la mediana.
# [ non aprire "daticlas": può contenere molti dati; eventualmente usa str(daticlass) ]
# Ma - sempre dopo aver battuto altrestat(), o dopo istogramma(…) - puoi più sempli-
# cemente battere: percentile(3)
#
# Posso confrontare boxplot relativi ad un dato fenomeno al passare, ad es., del tempo
# usando la stessa scala, assegnando l'intervallo in cui tracciare il boxplot a boxAB:
#
# altezze ventenni italiani maschi nel 1880 negli intervalli ampi 5 da 145 a 185 (cm)
# (tra 145 e 150 vi erano il 4% dei maschi, ...; sotto a 145 e sopra a 185
# le percentuali erano trascurabili)
freq1 <- c(4.0, 6.8, 20.4, 28.4, 23.5, 11.7, 3.7, 1.5)
interv1 <- seq(145,185, 5)
BF=4; HF=3; istoclas(interv1,freq1)
# ora dimensiono le finestre grafiche larghe e basse
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# altezze ventenni italiani maschi nel 1992 negli intervalli ampi 5 da 155 a 195 (cm)
freq2 <- c(1.7, 6.8, 18.6, 29.1, 25.2, 13.2, 4.3, 1.1)
interv2 <- seq(155,195, 5)
BF=4; HF=3; istoclas(interv2,freq2)
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# I boxplot ottenuti, a cui si sono aggiunte delle scritte:
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# Per avere altri percentili, dopo aver battuto altrestat(), puoi usare, ad es. per il
# 3° percentile, quantile(daticlas, 3/100). Con quantile(daticlas,1/2) hai la mediana.
# [ non aprire "daticlas": può contenere molti dati; eventualmente usa str(daticlass) ]
# Ma - sempre dopo aver battuto altrestat(), o dopo istogramma(…) - puoi più sempli-
# cemente battere: percentile(3)
#
# Posso confrontare boxplot relativi ad un dato fenomeno al passare, ad es., del tempo
# usando la stessa scala, assegnando l'intervallo in cui tracciare il boxplot a boxAB:
#
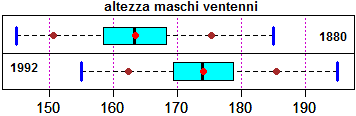
# altezze ventenni italiani maschi nel 1880 negli intervalli ampi 5 da 145 a 185 (cm)
# (tra 145 e 150 vi erano il 4% dei maschi, ...; sotto a 145 e sopra a 185
# le percentuali erano trascurabili)
freq1 <- c(4.0, 6.8, 20.4, 28.4, 23.5, 11.7, 3.7, 1.5)
interv1 <- seq(145,185, 5)
BF=4; HF=3; istoclas(interv1,freq1)
# ora dimensiono le finestre grafiche larghe e basse
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# altezze ventenni italiani maschi nel 1992 negli intervalli ampi 5 da 155 a 195 (cm)
freq2 <- c(1.7, 6.8, 18.6, 29.1, 25.2, 13.2, 4.3, 1.1)
interv2 <- seq(155,195, 5)
BF=4; HF=3; istoclas(interv2,freq2)
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# I boxplot ottenuti, a cui si sono aggiunte delle scritte:
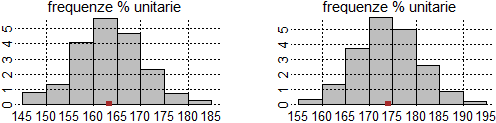
 # Gli istogrammi che si erano ottenuti con istoclass
# Gli istogrammi che si erano ottenuti con istoclass
 #
# Quando si hanno dati singoli che possono essere classificati in intervalli diversi
# può essere comodo rappresentarli con un istogramma di area 1, in modo che l'area di
# ogni colonnina corrisponda alla frequenza relativa di essa, come abbiamo visto si
# fa per i dati già classificati in intervalli (vedi qui). Per far questo si ricorre
# al comando hist. Ecco qualche esempio d'uso relativamente alle fave considerate nella
# prima parte di questo documento. dev.new() serve per aprire una nuova finestra,
# abline per tracciare linee parallele agli assi. Il numero delle classi viene scelto
# automaticamente o può essere precisato, approssimativamente, con nclass. Con cex.axis
# posso dimensionare i caratteri. right=FALSE specifica che gli intervalli in cui sono
# classificati i dati sono del tipo […,…).
# L'essenziale è: hist(fave, right=FALSE, probability=TRUE).
# "Density" indica che sull'asse y è rappresentata la densità di frequenza, ossia la
# frequenza percentuale unitaria (invece di probability=TRUE posso usare freq=FALSE).
dev.new()
hist(fave, nclass=5, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey")
abline(h=axTicks(2),lty=3)
# e quello che ottengo con nclass=20 e con nclass=10 (o senza specificare nclass)
#
# Quando si hanno dati singoli che possono essere classificati in intervalli diversi
# può essere comodo rappresentarli con un istogramma di area 1, in modo che l'area di
# ogni colonnina corrisponda alla frequenza relativa di essa, come abbiamo visto si
# fa per i dati già classificati in intervalli (vedi qui). Per far questo si ricorre
# al comando hist. Ecco qualche esempio d'uso relativamente alle fave considerate nella
# prima parte di questo documento. dev.new() serve per aprire una nuova finestra,
# abline per tracciare linee parallele agli assi. Il numero delle classi viene scelto
# automaticamente o può essere precisato, approssimativamente, con nclass. Con cex.axis
# posso dimensionare i caratteri. right=FALSE specifica che gli intervalli in cui sono
# classificati i dati sono del tipo […,…).
# L'essenziale è: hist(fave, right=FALSE, probability=TRUE).
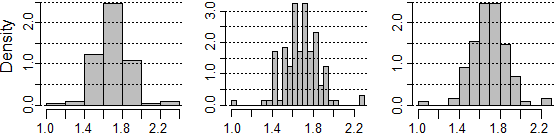
# "Density" indica che sull'asse y è rappresentata la densità di frequenza, ossia la
# frequenza percentuale unitaria (invece di probability=TRUE posso usare freq=FALSE).
dev.new()
hist(fave, nclass=5, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey")
abline(h=axTicks(2),lty=3)
# e quello che ottengo con nclass=20 e con nclass=10 (o senza specificare nclass)
 # Se vuoi aggiungere un istogramma in una pagina grafica aperta aggiungi alle opzioni
# ,add=TRUE Se non vuoi colorare la parte interna non mettere ,col=… Se vuoi colorare
# diversamente il bordo aggiungi ,border=… Per altro vedi gli approfondimenti.
# Per consoscere l'altezza di un istogramma (la densità massima), ad es. nel 1º caso:
max( hist(fave, nclass=5, right=FALSE, probability=TRUE, plot=FALSE)$density )
# 2.461538
# Ricordiamo che i valori di media e percentili relativi a dati non già classificati
# hanno senso solo se i dati sono arrotondati. Se ad es. ho dati troncati agli interi
# devo prima trasformarli aggiungendo 1/2 (dati = dati+1/2); se sono troncati ai decimi
# devo aggiungere 1/2 decimo (dati = dati+0.1/2); se sono troncati alle centininaia
# devo aggiungere 1/2 centinaia (dati = dati+100/2).
# Per simulare (con runif e sample, e set.seed) fenomeni e analizzare problemi probabi-
# listici (uso di Var, Sd, SdM, studio della gaussiana ed altre distribuzioni), e per
# (de)codificare messaggi, vedi gli approfondimenti (verso il fondo).
# Approfondimenti QUI
# Col comando analisiTesto(testo) posso analizzare statisticamente testi. Vedi qui come
# usare il comando (e le variabili maxIsto e maxIstoN, impiegabili per confrontare nella
# stessa scala istogrammi di fenomeni diversi). Sotto alcune delle uscite ottenibili
# confrontando lo stesso brano di "Alice nel paese delle meraviglie" in italiano e in
# inglese.
# Se vuoi aggiungere un istogramma in una pagina grafica aperta aggiungi alle opzioni
# ,add=TRUE Se non vuoi colorare la parte interna non mettere ,col=… Se vuoi colorare
# diversamente il bordo aggiungi ,border=… Per altro vedi gli approfondimenti.
# Per consoscere l'altezza di un istogramma (la densità massima), ad es. nel 1º caso:
max( hist(fave, nclass=5, right=FALSE, probability=TRUE, plot=FALSE)$density )
# 2.461538
# Ricordiamo che i valori di media e percentili relativi a dati non già classificati
# hanno senso solo se i dati sono arrotondati. Se ad es. ho dati troncati agli interi
# devo prima trasformarli aggiungendo 1/2 (dati = dati+1/2); se sono troncati ai decimi
# devo aggiungere 1/2 decimo (dati = dati+0.1/2); se sono troncati alle centininaia
# devo aggiungere 1/2 centinaia (dati = dati+100/2).
# Per simulare (con runif e sample, e set.seed) fenomeni e analizzare problemi probabi-
# listici (uso di Var, Sd, SdM, studio della gaussiana ed altre distribuzioni), e per
# (de)codificare messaggi, vedi gli approfondimenti (verso il fondo).
# Approfondimenti QUI
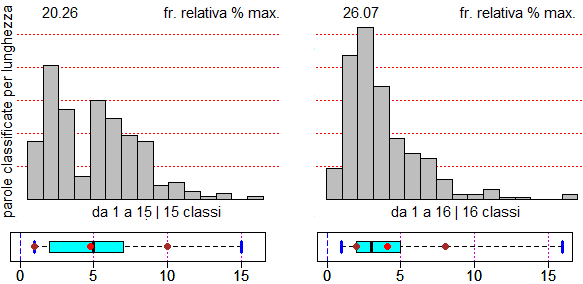
# Col comando analisiTesto(testo) posso analizzare statisticamente testi. Vedi qui come
# usare il comando (e le variabili maxIsto e maxIstoN, impiegabili per confrontare nella
# stessa scala istogrammi di fenomeni diversi). Sotto alcune delle uscite ottenibili
# confrontando lo stesso brano di "Alice nel paese delle meraviglie" in italiano e in
# inglese.
 # 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
# Oltre che grafici di funzioni di una variabile posso tracciare curve descritte come
# funzioni di due variabili, K(x,y)=0, mediante il comando curva(K, col). Esempi:
PIANO(-5,5, -5,5)
f <- function(x,y) y-(x^2-3); curva(f, "red")
g <- function(x,y) x-(y^2-3); curva(g, "blue")
h <- function(x,y) x^2+y^2-16; curva(h, "violet")
k <- function(x,y) x*y-1; cur(k, "black")
# Per altri modi di descrivere curve vedi qui [le coniche] e sotto il punto 27.
# Per risolvere eq. del tipo F(x,y)=0 rispetto ad x (fissato y=k) o ad y (fissato x=k)
# vedi qui.
# cur traccia le curve sottili.
# Analogamente graficF e grafic operano come graficoF e grafico ma con linee sottili
# grafiF e grafi le fanno di uno spessore intermedio
Piano(-5,5, -5,15)
q <- function(x) x^2-4; grafico(q,-5,5, "blue")
s <- function(x) x^2-2; grafic(s,-5,0, "red"); grafi(s,0,5, "seagreen")
# f, g, h, k q, s
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
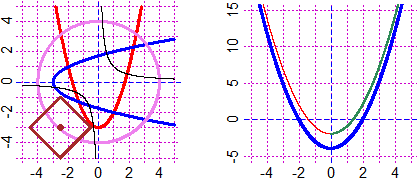
# Oltre che grafici di funzioni di una variabile posso tracciare curve descritte come
# funzioni di due variabili, K(x,y)=0, mediante il comando curva(K, col). Esempi:
PIANO(-5,5, -5,5)
f <- function(x,y) y-(x^2-3); curva(f, "red")
g <- function(x,y) x-(y^2-3); curva(g, "blue")
h <- function(x,y) x^2+y^2-16; curva(h, "violet")
k <- function(x,y) x*y-1; cur(k, "black")
# Per altri modi di descrivere curve vedi qui [le coniche] e sotto il punto 27.
# Per risolvere eq. del tipo F(x,y)=0 rispetto ad x (fissato y=k) o ad y (fissato x=k)
# vedi qui.
# cur traccia le curve sottili.
# Analogamente graficF e grafic operano come graficoF e grafico ma con linee sottili
# grafiF e grafi le fanno di uno spessore intermedio
Piano(-5,5, -5,15)
q <- function(x) x^2-4; grafico(q,-5,5, "blue")
s <- function(x) x^2-2; grafic(s,-5,0, "red"); grafi(s,0,5, "seagreen")
# f, g, h, k q, s
 #
# NOTA. I comandi grafico e graficoF impiegano abbastanza tempo a tracciare i grafici
# delle funzioni ad 1 input ma li fanno precisi. Vedi qui per prestare attenzione all'
# uso del comando curva e del comando plot (che non abbiamo discusso finora). Nella
# figura seguente vedi i grafici corretti di alcune funzioni che presentano dei salti
# ottenuti con grafico e quelli scorretti ottenuti con curva e con plot.
#
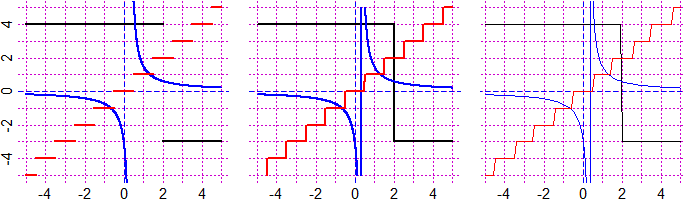
# NOTA. I comandi grafico e graficoF impiegano abbastanza tempo a tracciare i grafici
# delle funzioni ad 1 input ma li fanno precisi. Vedi qui per prestare attenzione all'
# uso del comando curva e del comando plot (che non abbiamo discusso finora). Nella
# figura seguente vedi i grafici corretti di alcune funzioni che presentano dei salti
# ottenuti con grafico e quelli scorretti ottenuti con curva e con plot.
 #
# Abbiamo visto come calcolare la distanza di un punto da un altro punto o una retta.
# Il comando distPF(x,y, F, a,b) calcola la distanza tra un punto x,y e il grafico di
# una funzione F ad 1 input e 1 output nel dominio a,b.
# Vediamo ad es. come calcolare le distanze seguenti, di (2,0) - punto blu - da K e G
# (voglio capire quale delle due curve è più vicina al punto):
#
# Abbiamo visto come calcolare la distanza di un punto da un altro punto o una retta.
# Il comando distPF(x,y, F, a,b) calcola la distanza tra un punto x,y e il grafico di
# una funzione F ad 1 input e 1 output nel dominio a,b.
# Vediamo ad es. come calcolare le distanze seguenti, di (2,0) - punto blu - da K e G
# (voglio capire quale delle due curve è più vicina al punto):
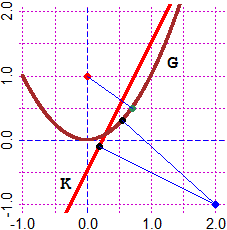 PIANO(-1,2, -1,2)
K <- function(x) 2*x-0.5; grafico(K,-1,2, "red")
G <- function(x) x^2; grafico(G,-1,2, "brown")
PUNTO(2,-1, "blue"); distPF(2,-1, K, -1,2)
distanza e punto più vicino:
# 2.012461 0.200000 -0.100000
PUNTO(0.2,-0.1, "black"); linea(0.2,-0.1, 2,-1, "blue")
# in questo caso la distanza l'avrei trovata anche col comando punto_retta
punto_retta(2,-1, 0,-1/2, 1,1.5)
# 2.012461
# Per G, che non ha come grafico una retta non posso farlo
distPF(2,-1, G, -1,2)
distanza e punto più vicino:
# 1.9490881 0.5535740 0.3064442
# Posso migliorare la precisione partendo da un intervallo più piccolo
distPF(2,-1, G, 0.5,0.6)
# 1.9490881 0.5535738 0.3064440
PUNTO(0.5535740, 0.3064442, 1); linea(0.5535740, 0.3064442, 2,-1, "blue")
# È più vicina la curva G
# Calcoliamo la distanza del punto rosso, (0,1), da G:
PUNTO(0,1, "red"); distPF(0,1, G, -1,2)
# 0.8660254 -0.7071070 0.5000003 Miglioro la precisione:
distPF(0,1, G, -0.8,-0.6)
# 0.8660254 -0.7071068 0.5000000 Oltre a 0.866... anche 0.707… e 0.5 mi
# sembrano delle radici quadrate di frazioni tra interi. Verifico:
frazio(distPF(0,1, G, -0.8,-0.6)^2)
# 0.8660254 -0.7071068 0.5000000
# 3/4 1/2 1/4 La distanza è √3/2
# Traccio (0.707…, 0.5)
PUNTO(sqrt(1/2), 1/2, "seagreen"); linea(0,1, sqrt(1/2),1/2, "blue")
#
# NOTA: curva(h,...) per fare il grafico di h(x,y)=0 cerca dove h cambia
# segno; se ovunque h(x,y)≥0 o h(x,y)≤0 il grafico non viene tracciato.
# Prova allora a fare quello di abs(h(x,y))-eps = 0 con eps piccolo.
# Un esempio facile, per capire:
PIANO(-4,4, -4,4)
g <- function(x,y) x^2+4*y^2-4*x*y; curva(g,"green")
# non ottengo nulla ( anche se in questo caso so che la curva
# è x-2*y = 0 in quanto x^2+4*y^2-4*x*y = (x-2*y)^2 )
eps <- 1e-4; k <- function(x,y) abs(g(x,y))-eps; curva(k,"blue")
PIANO(-1,2, -1,2)
K <- function(x) 2*x-0.5; grafico(K,-1,2, "red")
G <- function(x) x^2; grafico(G,-1,2, "brown")
PUNTO(2,-1, "blue"); distPF(2,-1, K, -1,2)
distanza e punto più vicino:
# 2.012461 0.200000 -0.100000
PUNTO(0.2,-0.1, "black"); linea(0.2,-0.1, 2,-1, "blue")
# in questo caso la distanza l'avrei trovata anche col comando punto_retta
punto_retta(2,-1, 0,-1/2, 1,1.5)
# 2.012461
# Per G, che non ha come grafico una retta non posso farlo
distPF(2,-1, G, -1,2)
distanza e punto più vicino:
# 1.9490881 0.5535740 0.3064442
# Posso migliorare la precisione partendo da un intervallo più piccolo
distPF(2,-1, G, 0.5,0.6)
# 1.9490881 0.5535738 0.3064440
PUNTO(0.5535740, 0.3064442, 1); linea(0.5535740, 0.3064442, 2,-1, "blue")
# È più vicina la curva G
# Calcoliamo la distanza del punto rosso, (0,1), da G:
PUNTO(0,1, "red"); distPF(0,1, G, -1,2)
# 0.8660254 -0.7071070 0.5000003 Miglioro la precisione:
distPF(0,1, G, -0.8,-0.6)
# 0.8660254 -0.7071068 0.5000000 Oltre a 0.866... anche 0.707… e 0.5 mi
# sembrano delle radici quadrate di frazioni tra interi. Verifico:
frazio(distPF(0,1, G, -0.8,-0.6)^2)
# 0.8660254 -0.7071068 0.5000000
# 3/4 1/2 1/4 La distanza è √3/2
# Traccio (0.707…, 0.5)
PUNTO(sqrt(1/2), 1/2, "seagreen"); linea(0,1, sqrt(1/2),1/2, "blue")
#
# NOTA: curva(h,...) per fare il grafico di h(x,y)=0 cerca dove h cambia
# segno; se ovunque h(x,y)≥0 o h(x,y)≤0 il grafico non viene tracciato.
# Prova allora a fare quello di abs(h(x,y))-eps = 0 con eps piccolo.
# Un esempio facile, per capire:
PIANO(-4,4, -4,4)
g <- function(x,y) x^2+4*y^2-4*x*y; curva(g,"green")
# non ottengo nulla ( anche se in questo caso so che la curva
# è x-2*y = 0 in quanto x^2+4*y^2-4*x*y = (x-2*y)^2 )
eps <- 1e-4; k <- function(x,y) abs(g(x,y))-eps; curva(k,"blue")
 # Posso provare a fare automaticamente ciò col comando seguente ("n" sta per nulla):
curvan(g,1,"red") # o curvan(g,N,col) con N > 1 o < 1, o curn per una curva sottile
#
# Posso tracciare griglie e indicare le scale in forma non decimale. Questo può essere
# utile, ad esempio, nel caso di funzioni trigonometriche, ma non solo. Si possono
# indicare le distanze tra i lati della griglia coi comandi TACCHEx e TACCHEy e usare
# i comandi Piano2 o PIANO2 per tracciare la parte di piano cartesiano voluta. Vedi
# qui per ottenere grafici come il seguente:
# Posso provare a fare automaticamente ciò col comando seguente ("n" sta per nulla):
curvan(g,1,"red") # o curvan(g,N,col) con N > 1 o < 1, o curn per una curva sottile
#
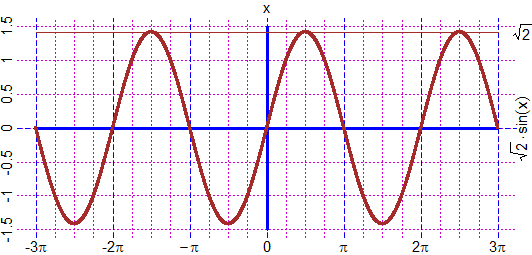
# Posso tracciare griglie e indicare le scale in forma non decimale. Questo può essere
# utile, ad esempio, nel caso di funzioni trigonometriche, ma non solo. Si possono
# indicare le distanze tra i lati della griglia coi comandi TACCHEx e TACCHEy e usare
# i comandi Piano2 o PIANO2 per tracciare la parte di piano cartesiano voluta. Vedi
# qui per ottenere grafici come il seguente:
 # 23 Risolvere equazioni (soluz).
# Se hai un'equazione del tipo F(x)=G(x) puoi risolverla definendo H come F-G e usando
# soluz. Ma puoi più anche usare soluz2(F,G, a,b) se la soluzione è tra a e b:
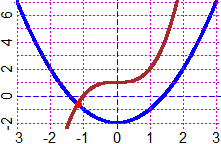
f <- function(x) x^2-2; g <- function(x) x^3+1
graficoF(f, -3,3, "blue"); grafico(g, -3,3, "brown")
x <- soluz2(f,g, -2,0); x; piu(x); punto(x,f(x), "red")
# -1.174559 -1.17455941029298
# 23 Risolvere equazioni (soluz).
# Se hai un'equazione del tipo F(x)=G(x) puoi risolverla definendo H come F-G e usando
# soluz. Ma puoi più anche usare soluz2(F,G, a,b) se la soluzione è tra a e b:
f <- function(x) x^2-2; g <- function(x) x^3+1
graficoF(f, -3,3, "blue"); grafico(g, -3,3, "brown")
x <- soluz2(f,g, -2,0); x; piu(x); punto(x,f(x), "red")
# -1.174559 -1.17455941029298
 # Puoi anche ricorrere a WolframAlpha, ma le uscite non sono sempre facili da
# interpretare: vedi.
#
# Puoi risolvere le equazioni polinomiali in cui l'unica variabile che compare è l'
# incognita: soluzione di -78 + 73*x - 57*x^2 + 73*x^3 + 21*x^4 = 0
# ( occorre mettere i coefficienti per grado crescente )
q <- c(-78, 73, -57, 73, 21); solpol(q)
# 0.857142857142857 -4.33333333333333
# Le uscite sono temporaneamente messe in soluzione
a = soluzione[1]; b = soluzione[2]; a; piu( b)
# 0.8571429 -4.33333333333333
frazio( soluzione )
# 6/7 -13/3
# Controllo grafico (vedi sotto a sinistra):
f <- function(x) -78+73*x-57*x^2+73*x^3+21*x^4
graficoF(f, -5,2, "blue")# Altro esempio: soluzione di -2/9 - 2/9*x + x^3 + x^4 = 0
# Non c'è il termine di grado 2: metto 0 al suo posto
u <- c(-2/9, -2/9, 0, 1, 1); solpol(u)
# 0.60570686427738 -1
f <- function(x) -2/9 - 2/9*x + x^3 + x^4
graficoF(f, -1.5,1, "blue")
PUNTO(soluzione,c(0,0), "red")
# Per avere anche le soluzioni complesse (vedi qui per i numeri complessi) si usa:
u <- c(-2/9, -2/9, 0, 1, 1); polyroot(u)
# 0.6057069-0i -0.3028534+0.5245575i -0.3028534-0.5245575i -1+0i
# Per il calcolo polinomiale più complesso conviene ricorrere a Wolframalpha (vedi):
# basta che metta:
# quotient and remainder of (x^5 + x^3 - 1) / (x^2 + x - 5)
# per ottenere: quotient: x^3 - x^2 + 7*x - 12 remainder: 47*x - 61
# o (x^5 + x^3 - 1) * (x^2 + x - 5) per avere
# x^7 + x^6 - 4*x^5 + x^4 - 5*x^3 - x^2 - x + 5
# o simplify (x^2 + 1) / (x^5 - x) per avere 1/(x^3 - x)
# [ Qui considero polinomi in una sola indeterminata in cui non appaiono altre variabi-
# li. Se considero ad es. a*x+a*y-y-x come polinomio in una indeterminata devo spe-
# cificare qual è essa (il concetto di polinomio "senza indeterminate" non ha senso).
# Ecco cosa accade con WolframAlpha usando il comando Collect:
# Collect[ a*x+a*y-y-x, a] dà a*(x+y)-x-y, Collect[ a*x+a*y-y-x, x] dà (a-1)*x+a*y-y,
# Collect[ a*x+a*y-y-x, y] dà (a-1)*y+a*x-x. Collect[ u*x^2+u*x+x+u,u] dà
# u*(x^2+x+1)+x, Collect[ u*x^2+u*x+x+u,x] dà u*x^2+(u+1)*x+u. Vedi qui, anche
# per fattorizzare o semplificare termini: factor a^2-b^2 -> (a-b)*(a+b),
# expand (a-b)*(a+b) -> a^2-b^2 ]
# Puoi comunque sommare e moltiplicare polinomi con sommap e prodp. Per operare su
# P = x^5 + x^3 - 1 e Q = x^2 + x - 5 e trovarne somma e prodotto dai come input i
# coefficienti (occorre metterli per grado decrescente):
P <- c(1,0,1,0,0,-1); Q <- c(1,1,-5)
# e fai:
sommap(P,Q); prodp(P,Q); sommap(P,-2*Q) # ho anche sottratto da P il doppio di Q
# 1 0 1 1 1 -6
# 1 1 -4 1 -5 -1 -1 5
# 1 0 1 -2 -2 9
# Hai x^5+x^3+x^2+x-6 x^7+x^6-4x^5+x^4-5x^3-x^2-x+5 x^5+x^3-2x^2-2x+9
# Per trovare (x+1)^7 moltiplica 7 volte 1 per x+1:
A <- 1; B <- c(1,1); for(i in 1:7) A <- prodp(A,B); A
# 1 7 21 35 35 21 7 1
# Ovvero: 1 + 7x + 21x^2 + 35x^3 + 35x^4 + 21x^5 + 7x^6 + x^7
# Per il significato di "for" vedi qui sotto
#
# Per ripetere più volte una sequenza di comandi o modificare l'esecuzione a seconda
# del valore di certe variabili si usano i comandi: if, ifelse, for, while. È inoltre
# spesso utile ricorrere ai connettivi. Vediamo cosa sono con dei semplici esempi.
#
for(i in -2:2) if(i > 0) print(i)
# 1 2
for(i in -2:2) if(i >= 0) print(i)
# 0 1 2
for(i in -2:2) if(i == 0) print(i)
# 0
for(i in -2:2) if(i != 0) print(i)
# -2 -1 1 2
for(i in -2:2) if( !(i==0) ) print(i)
# -2 -1 1 2
for(i in -2:2) if(i > 0 | i <0) print(i)
# -2 -1 1 2
for(i in -2:2) if(i >= 0 & i <= 0) print(i)
# 0
for(i in -2:2) if(i == 0) print(i) else print (1/i)
# -0.5 -1 0 1 0.5
for(i in -2:2) print( ifelse(i==0, i, 1/i) )
# -0.5 -1 0 1 0.5
for(k in c(1,5,10,50)) print(1/k)
# 1 0.2 0.1 0.02
n = 5; k = n; p = 1; while(k > 0) {print(k); p = p*k; k = k-1}; p
# 5 4 3 2 1 120
p = 1; n = 1; while(TRUE) {if(p > 10000) break else {print(p); n=n+1; p = p*n} }
# 1 2 6 24 120 720 5040
# { e } consentono di raggruppare più istruzioni. Cerca di capire da solo cosa fanno i
# vari comandi e, poi, usa help("if") help("ifelse") help("&") help("TRUE")
#
# ifelse è impiegato spesso per definire funzioni da calcolare in modi diversi
# in diversi parti del dominio. Un semplice esempio:
H = function(x) ifelse(x<5, -2, ifelse(x>10, x*2, x) )
# vale -2 per x<5, 2x per x>10, x altrove, ossia in [5,10]
BF=2.5; HF=2; graficoF(H, -5, 15, "blue")
# Puoi anche ricorrere a WolframAlpha, ma le uscite non sono sempre facili da
# interpretare: vedi.
#
# Puoi risolvere le equazioni polinomiali in cui l'unica variabile che compare è l'
# incognita: soluzione di -78 + 73*x - 57*x^2 + 73*x^3 + 21*x^4 = 0
# ( occorre mettere i coefficienti per grado crescente )
q <- c(-78, 73, -57, 73, 21); solpol(q)
# 0.857142857142857 -4.33333333333333
# Le uscite sono temporaneamente messe in soluzione
a = soluzione[1]; b = soluzione[2]; a; piu( b)
# 0.8571429 -4.33333333333333
frazio( soluzione )
# 6/7 -13/3
# Controllo grafico (vedi sotto a sinistra):
f <- function(x) -78+73*x-57*x^2+73*x^3+21*x^4
graficoF(f, -5,2, "blue")# Altro esempio: soluzione di -2/9 - 2/9*x + x^3 + x^4 = 0
# Non c'è il termine di grado 2: metto 0 al suo posto
u <- c(-2/9, -2/9, 0, 1, 1); solpol(u)
# 0.60570686427738 -1
f <- function(x) -2/9 - 2/9*x + x^3 + x^4
graficoF(f, -1.5,1, "blue")
PUNTO(soluzione,c(0,0), "red")
# Per avere anche le soluzioni complesse (vedi qui per i numeri complessi) si usa:
u <- c(-2/9, -2/9, 0, 1, 1); polyroot(u)
# 0.6057069-0i -0.3028534+0.5245575i -0.3028534-0.5245575i -1+0i
# Per il calcolo polinomiale più complesso conviene ricorrere a Wolframalpha (vedi):
# basta che metta:
# quotient and remainder of (x^5 + x^3 - 1) / (x^2 + x - 5)
# per ottenere: quotient: x^3 - x^2 + 7*x - 12 remainder: 47*x - 61
# o (x^5 + x^3 - 1) * (x^2 + x - 5) per avere
# x^7 + x^6 - 4*x^5 + x^4 - 5*x^3 - x^2 - x + 5
# o simplify (x^2 + 1) / (x^5 - x) per avere 1/(x^3 - x)
# [ Qui considero polinomi in una sola indeterminata in cui non appaiono altre variabi-
# li. Se considero ad es. a*x+a*y-y-x come polinomio in una indeterminata devo spe-
# cificare qual è essa (il concetto di polinomio "senza indeterminate" non ha senso).
# Ecco cosa accade con WolframAlpha usando il comando Collect:
# Collect[ a*x+a*y-y-x, a] dà a*(x+y)-x-y, Collect[ a*x+a*y-y-x, x] dà (a-1)*x+a*y-y,
# Collect[ a*x+a*y-y-x, y] dà (a-1)*y+a*x-x. Collect[ u*x^2+u*x+x+u,u] dà
# u*(x^2+x+1)+x, Collect[ u*x^2+u*x+x+u,x] dà u*x^2+(u+1)*x+u. Vedi qui, anche
# per fattorizzare o semplificare termini: factor a^2-b^2 -> (a-b)*(a+b),
# expand (a-b)*(a+b) -> a^2-b^2 ]
# Puoi comunque sommare e moltiplicare polinomi con sommap e prodp. Per operare su
# P = x^5 + x^3 - 1 e Q = x^2 + x - 5 e trovarne somma e prodotto dai come input i
# coefficienti (occorre metterli per grado decrescente):
P <- c(1,0,1,0,0,-1); Q <- c(1,1,-5)
# e fai:
sommap(P,Q); prodp(P,Q); sommap(P,-2*Q) # ho anche sottratto da P il doppio di Q
# 1 0 1 1 1 -6
# 1 1 -4 1 -5 -1 -1 5
# 1 0 1 -2 -2 9
# Hai x^5+x^3+x^2+x-6 x^7+x^6-4x^5+x^4-5x^3-x^2-x+5 x^5+x^3-2x^2-2x+9
# Per trovare (x+1)^7 moltiplica 7 volte 1 per x+1:
A <- 1; B <- c(1,1); for(i in 1:7) A <- prodp(A,B); A
# 1 7 21 35 35 21 7 1
# Ovvero: 1 + 7x + 21x^2 + 35x^3 + 35x^4 + 21x^5 + 7x^6 + x^7
# Per il significato di "for" vedi qui sotto
#
# Per ripetere più volte una sequenza di comandi o modificare l'esecuzione a seconda
# del valore di certe variabili si usano i comandi: if, ifelse, for, while. È inoltre
# spesso utile ricorrere ai connettivi. Vediamo cosa sono con dei semplici esempi.
#
for(i in -2:2) if(i > 0) print(i)
# 1 2
for(i in -2:2) if(i >= 0) print(i)
# 0 1 2
for(i in -2:2) if(i == 0) print(i)
# 0
for(i in -2:2) if(i != 0) print(i)
# -2 -1 1 2
for(i in -2:2) if( !(i==0) ) print(i)
# -2 -1 1 2
for(i in -2:2) if(i > 0 | i <0) print(i)
# -2 -1 1 2
for(i in -2:2) if(i >= 0 & i <= 0) print(i)
# 0
for(i in -2:2) if(i == 0) print(i) else print (1/i)
# -0.5 -1 0 1 0.5
for(i in -2:2) print( ifelse(i==0, i, 1/i) )
# -0.5 -1 0 1 0.5
for(k in c(1,5,10,50)) print(1/k)
# 1 0.2 0.1 0.02
n = 5; k = n; p = 1; while(k > 0) {print(k); p = p*k; k = k-1}; p
# 5 4 3 2 1 120
p = 1; n = 1; while(TRUE) {if(p > 10000) break else {print(p); n=n+1; p = p*n} }
# 1 2 6 24 120 720 5040
# { e } consentono di raggruppare più istruzioni. Cerca di capire da solo cosa fanno i
# vari comandi e, poi, usa help("if") help("ifelse") help("&") help("TRUE")
#
# ifelse è impiegato spesso per definire funzioni da calcolare in modi diversi
# in diversi parti del dominio. Un semplice esempio:
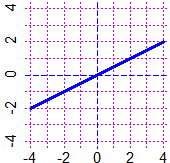
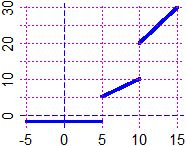
H = function(x) ifelse(x<5, -2, ifelse(x>10, x*2, x) )
# vale -2 per x<5, 2x per x>10, x altrove, ossia in [5,10]
BF=2.5; HF=2; graficoF(H, -5, 15, "blue")
 ## PARTI NUOVE
# 24 Calcolo approssimato
# (vedi il punto 31 per la rappresentazione grafica delle approssimazioni)
# Con le operazioni + - * / ^ posso procedere così:
# Area del rettangolo con lati A e B tra 30.5 e 31.5 e tra 1.3 e 1.4 centimetri
approssima( c(30.5,31.5), c(1.3,1.4), "*")
# [1] min [2] max
# 39.650 44.100
approssima2( c(30.5,31.5), c(1.3,1.4), "*")
# [1] centro [2] raggio
# 41.875 2.225
# Sta nell'intervallo [39.65 cm², 44.10 cm²], o: 41.9 ± 2.3 cm²
# Stesse cose per +, -, /, ^.
# Se uno dei due fattori è esatto posso metterlo direttamente:
x = 2.1 ± 0.1, y = 2.9 ± 0.1, 1/z = 1/x + 1/y. Quanto vale z?
x <- c(2.0,2.2); y <- c(2.8,3.0)
rx <- approssima(1,x, "/") # reciproco di x
ry <- approssima(1,y, "/")
rz <- approssima(rx,ry, "+")
z <- approssima(1,rz, "/"); z
# [1] min [2] max
# 1.166667 1.269231
# o:
approssima2(1,rz, "/")
# [1] centro [2] raggio
# 1.21794872 0.05128205 ovvero: 1.22±0.06
# In altri casi, per una qualunque funzione, posso procedere come sotto illustrato, im-
# piegando EPS(r) che genera a caso molti valori tra 0 ed r. Esempi:
# So che A = 10±2; B = 30±2; C = 20±1. Quanto vale A*B/C?
A=10+EPS(2); B=30+EPS(2); C=20+EPS(1)
f = function(x,y,z) x*y/z
min( f(A,B,C) ); max( f(A,B,C) )
# 10.67832 20.19008
# Se voglio una stima migliore (impiegando qualche secondo in più):
A=10+EPS2(2); B=30+EPS2(2); C=20+EPS2(1)
f = function(x,y,z) x*y/z; min( f(A,B,C) ); max( f(A,B,C) )
# 10.67067 20.19745
# Concludo che A*B/C è compreso tra 10.6 e 20.2, o che è 15.5±5
# (nota: in qualche libro di laboratorio di fisica per lo stesso problema si trova,
# usando a sproposito complesse tecniche di calcolo differenziale, 15±3.25, ossia
# un intervallo più piccolo e scentrato!!!).
# Invero in questo caso potrei procedere anche "a mano" calcolando (10-2)*(30-2)/(20+1)
# e (10+2)*(30+2)/(20-1).
# Altro esempio. Una bilia è lanciata in aria con velocità inziale v = 4±0.1 m/s.
# Dopo t = 0.6±0.06 s ha raggiunto l'altezza h = v*t-g*t^2/2, dove g = 9.80±0.001 m/s^2.
# Quanto vale h?
t = 0.6+EPS(0.06); v = 4+EPS(0.1); g = 9.8+EPS(0.001)
h = function(t,v,g) v*t-g*t^2/2; m=min( h(t,v,g) ); M=max( h(t,v,g) ); m; M
# 0.4394424 0.7851418 h sta tra questi due valori, ovvero:
(m+M)/2; (M-m)/2
# 0.6122921 0.1728497, cioè h = 0.612 +/- 0.173, ovvero h = 0.6 +/- 0.2 (metri)
# (non hanno senso le soluzioni con molte cifre che si trovano in parecchi manuali)
# 25 Animazioni e altro su Finestre e Punti. Centroide (baricentro)
# boxN apre un nuovo sistema di coordinate senza niente, né griglia né assi, riempendo
# la finestra (senza lo spazio usualmente impiegato per le coordinate). BoxN fa lo
# stesso nella finestra attualmente aperta. boxmN e BoxmN fanno lo stesso usando una
# scala monometrica. boxNN opera come boxN lasciando un margine superiore e a destra.
# Possono essere utili anche per figure animate. Esempio: (vedi qui per "attendi")
HF=3; BF=3
boxN(0,100, 0,100)
for (k in 0:10) { BoxN(0,100, 0,100)
cerchio(50,82, 7, "brown"); text(50,95,"aspetta")
spezzata( c(55,50,50),c(0,0,75), "blue" ); attendi(0.5)
BoxN(0,100, 0,100)
cerchio(50,82, 7, "brown"); text(50,95,"aspetta")
spezzata( c(35,30,50,70,75,70,50,50,35,50,65),
c(1.5,2,40,2,2.5, 2,40,75,45,75,45), "blue" );
attendi(0.5) }
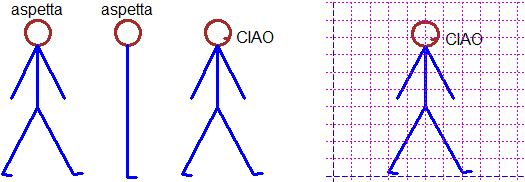
spezzata(c(53.5,55.85),c(79,79), "brown"); text(71,80,"CIAO"); CANCELLA(0,100, 90,100)
# ho aggiunto la bocca e la scritta "CIAO"; ho cancellato "aspetta"
# CANCELLA sovrappone un rettangolo bianco a quanto appare sulla finestra (in questo
# caso orizzontalmente da 0 a 100 e verticalmente da 90 a 100).
## PARTI NUOVE
# 24 Calcolo approssimato
# (vedi il punto 31 per la rappresentazione grafica delle approssimazioni)
# Con le operazioni + - * / ^ posso procedere così:
# Area del rettangolo con lati A e B tra 30.5 e 31.5 e tra 1.3 e 1.4 centimetri
approssima( c(30.5,31.5), c(1.3,1.4), "*")
# [1] min [2] max
# 39.650 44.100
approssima2( c(30.5,31.5), c(1.3,1.4), "*")
# [1] centro [2] raggio
# 41.875 2.225
# Sta nell'intervallo [39.65 cm², 44.10 cm²], o: 41.9 ± 2.3 cm²
# Stesse cose per +, -, /, ^.
# Se uno dei due fattori è esatto posso metterlo direttamente:
x = 2.1 ± 0.1, y = 2.9 ± 0.1, 1/z = 1/x + 1/y. Quanto vale z?
x <- c(2.0,2.2); y <- c(2.8,3.0)
rx <- approssima(1,x, "/") # reciproco di x
ry <- approssima(1,y, "/")
rz <- approssima(rx,ry, "+")
z <- approssima(1,rz, "/"); z
# [1] min [2] max
# 1.166667 1.269231
# o:
approssima2(1,rz, "/")
# [1] centro [2] raggio
# 1.21794872 0.05128205 ovvero: 1.22±0.06
# In altri casi, per una qualunque funzione, posso procedere come sotto illustrato, im-
# piegando EPS(r) che genera a caso molti valori tra 0 ed r. Esempi:
# So che A = 10±2; B = 30±2; C = 20±1. Quanto vale A*B/C?
A=10+EPS(2); B=30+EPS(2); C=20+EPS(1)
f = function(x,y,z) x*y/z
min( f(A,B,C) ); max( f(A,B,C) )
# 10.67832 20.19008
# Se voglio una stima migliore (impiegando qualche secondo in più):
A=10+EPS2(2); B=30+EPS2(2); C=20+EPS2(1)
f = function(x,y,z) x*y/z; min( f(A,B,C) ); max( f(A,B,C) )
# 10.67067 20.19745
# Concludo che A*B/C è compreso tra 10.6 e 20.2, o che è 15.5±5
# (nota: in qualche libro di laboratorio di fisica per lo stesso problema si trova,
# usando a sproposito complesse tecniche di calcolo differenziale, 15±3.25, ossia
# un intervallo più piccolo e scentrato!!!).
# Invero in questo caso potrei procedere anche "a mano" calcolando (10-2)*(30-2)/(20+1)
# e (10+2)*(30+2)/(20-1).
# Altro esempio. Una bilia è lanciata in aria con velocità inziale v = 4±0.1 m/s.
# Dopo t = 0.6±0.06 s ha raggiunto l'altezza h = v*t-g*t^2/2, dove g = 9.80±0.001 m/s^2.
# Quanto vale h?
t = 0.6+EPS(0.06); v = 4+EPS(0.1); g = 9.8+EPS(0.001)
h = function(t,v,g) v*t-g*t^2/2; m=min( h(t,v,g) ); M=max( h(t,v,g) ); m; M
# 0.4394424 0.7851418 h sta tra questi due valori, ovvero:
(m+M)/2; (M-m)/2
# 0.6122921 0.1728497, cioè h = 0.612 +/- 0.173, ovvero h = 0.6 +/- 0.2 (metri)
# (non hanno senso le soluzioni con molte cifre che si trovano in parecchi manuali)
# 25 Animazioni e altro su Finestre e Punti. Centroide (baricentro)
# boxN apre un nuovo sistema di coordinate senza niente, né griglia né assi, riempendo
# la finestra (senza lo spazio usualmente impiegato per le coordinate). BoxN fa lo
# stesso nella finestra attualmente aperta. boxmN e BoxmN fanno lo stesso usando una
# scala monometrica. boxNN opera come boxN lasciando un margine superiore e a destra.
# Possono essere utili anche per figure animate. Esempio: (vedi qui per "attendi")
HF=3; BF=3
boxN(0,100, 0,100)
for (k in 0:10) { BoxN(0,100, 0,100)
cerchio(50,82, 7, "brown"); text(50,95,"aspetta")
spezzata( c(55,50,50),c(0,0,75), "blue" ); attendi(0.5)
BoxN(0,100, 0,100)
cerchio(50,82, 7, "brown"); text(50,95,"aspetta")
spezzata( c(35,30,50,70,75,70,50,50,35,50,65),
c(1.5,2,40,2,2.5, 2,40,75,45,75,45), "blue" );
attendi(0.5) }
spezzata(c(53.5,55.85),c(79,79), "brown"); text(71,80,"CIAO"); CANCELLA(0,100, 90,100)
# ho aggiunto la bocca e la scritta "CIAO"; ho cancellato "aspetta"
# CANCELLA sovrappone un rettangolo bianco a quanto appare sulla finestra (in questo
# caso orizzontalmente da 0 a 100 e verticalmente da 90 a 100).
 # Se poi voglio vedere griglia e assi basta che batta BOX(), che li sovrappone alla
# immagine che compare nell'ultima finestra grafica. BOXs() la traccia senza assi,
# BOXg() la traccia con gli assi più grandi, ossia più spessi.
# Qui puoi vederne un altro esempio.
# Se poi voglio vedere griglia e assi basta che batta BOX(), che li sovrappone alla
# immagine che compare nell'ultima finestra grafica. BOXs() la traccia senza assi,
# BOXg() la traccia con gli assi più grandi, ossia più spessi.
# Qui puoi vederne un altro esempio.
 # Per una "quasi" animazione, batti Quadrilatero(a,b,c,d) dove al posto di a,b,c,d
# metti le direzioni in cui sono posti i vertici (in °, tra 0 e 360)
# Per una "quasi" animazione, batti Quadrilatero(a,b,c,d) dove al posto di a,b,c,d
# metti le direzioni in cui sono posti i vertici (in °, tra 0 e 360)
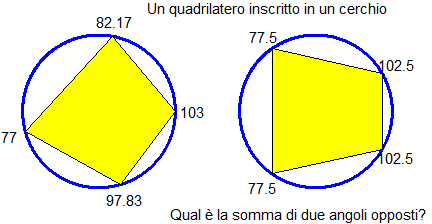 # [ la prima figura è stata ottenuta con Quadrilatero(0,80,195.67,286) ]
# [PianoN e PIANON operano in modo simile a BoxN e BoxmN]
# Per animazioni in cui vi siano assi e coordinate convengono i comandi recordPlot e
# replayPlot visti in 12. Vedi qui per un esempio. Vedi anche Esempi-27.
# Per relizzare animazioni con sistemi di riferimento che mutano puoi usare dev.off()
# e dev.new() che, rispettivamente, chiudono l'ultima finestra e ne aprono una nuova.
# NF() predispone una nuova finestra delle stesse dimensioni dell'ultima usata.
# PPP() memorizza come xP e yP le coord. del punto cliccato
# puntiB, puntiniB, punticiniB, palliniB scelgono automaticamente il box,
# puntiBm, puntiniBm, punticiniBm, palliniBm lo scelgono monometrico.
# Spezzata e Spezza a differenza di spezzata e spezza non connettono le "y".
# spezzat opera come spezza ma tratteggia i segmenti.
# Spezzat opera come spezza ma fa i segmenti un po' più spessi.
BF <- 2; HF <- 2; x <- c(0,2,3,6); y <- c(1,2,4,5)
PIANO(0,6,0,6); spezzata(x,y, "blue"); PIANO(0,6,0,6); Spezzata(x,y, "blue")
PIANO(0,6,0,6); spezzat(x,y, "red"); PIANO(0,6,0,6); Spezzat(x,y, "seagreen")
# [ la prima figura è stata ottenuta con Quadrilatero(0,80,195.67,286) ]
# [PianoN e PIANON operano in modo simile a BoxN e BoxmN]
# Per animazioni in cui vi siano assi e coordinate convengono i comandi recordPlot e
# replayPlot visti in 12. Vedi qui per un esempio. Vedi anche Esempi-27.
# Per relizzare animazioni con sistemi di riferimento che mutano puoi usare dev.off()
# e dev.new() che, rispettivamente, chiudono l'ultima finestra e ne aprono una nuova.
# NF() predispone una nuova finestra delle stesse dimensioni dell'ultima usata.
# PPP() memorizza come xP e yP le coord. del punto cliccato
# puntiB, puntiniB, punticiniB, palliniB scelgono automaticamente il box,
# puntiBm, puntiniBm, punticiniBm, palliniBm lo scelgono monometrico.
# Spezzata e Spezza a differenza di spezzata e spezza non connettono le "y".
# spezzat opera come spezza ma tratteggia i segmenti.
# Spezzat opera come spezza ma fa i segmenti un po' più spessi.
BF <- 2; HF <- 2; x <- c(0,2,3,6); y <- c(1,2,4,5)
PIANO(0,6,0,6); spezzata(x,y, "blue"); PIANO(0,6,0,6); Spezzata(x,y, "blue")
PIANO(0,6,0,6); spezzat(x,y, "red"); PIANO(0,6,0,6); Spezzat(x,y, "seagreen")
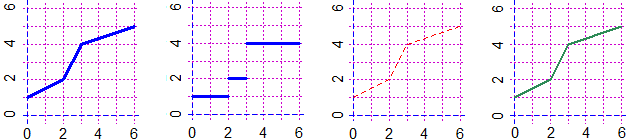 puntiB(x,y, "red"); puntiBm(x,y, "red")
puntiB(x,y, "red"); puntiBm(x,y, "red")


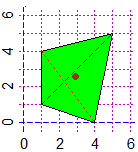 # Sopra come è possibile tracciare altri tipi di punti ("D" come "Delta"):
PIANO(0,6,0,6); puntoO(1,1,"blue"); puntoV(3,3,"red"); puntoD(4,2,"black")
# puntiO/V/D(x,y,col) se sono messi in x,y più punti, non li collegano
# Linea e LInea a differenza di linea, che traccia i segmenti come segm ma sottili,
# tratteggiano i segmenti (con tratto corto/lungo).
# Con centroPol(x,y) ho il centroide del poligono "x,y" (vedi sopra figura a destra).
BF <- 2; HF <- 2; x <- c(1,4,5,1); y <- c(1,0,5,4)
PIANO(0,6,0,6); spezzaC(x,y,"green"); Linea(1,4, 4,0, "red"); LInea(1,1, 5,5, "blue")
centroPol(x,y); PUNTI(centroPol(x,y)[1],centroPol(x,y)[2],"brown")
# [1] 2.904762 2.571429
# Nel caso di masse isolate m1, m2, … posizionate nei punti x1,y1, x2,y2, …, posto
# m = c(m1,m2,…), x = c(x1,x2,…), y = c(y1,y2,…), le coordinate del baricentro sono:
sum(m*x)/sum(m); sum(m*y)/sum(m)
# Sopra come è possibile tracciare altri tipi di punti ("D" come "Delta"):
PIANO(0,6,0,6); puntoO(1,1,"blue"); puntoV(3,3,"red"); puntoD(4,2,"black")
# puntiO/V/D(x,y,col) se sono messi in x,y più punti, non li collegano
# Linea e LInea a differenza di linea, che traccia i segmenti come segm ma sottili,
# tratteggiano i segmenti (con tratto corto/lungo).
# Con centroPol(x,y) ho il centroide del poligono "x,y" (vedi sopra figura a destra).
BF <- 2; HF <- 2; x <- c(1,4,5,1); y <- c(1,0,5,4)
PIANO(0,6,0,6); spezzaC(x,y,"green"); Linea(1,4, 4,0, "red"); LInea(1,1, 5,5, "blue")
centroPol(x,y); PUNTI(centroPol(x,y)[1],centroPol(x,y)[2],"brown")
# [1] 2.904762 2.571429
# Nel caso di masse isolate m1, m2, … posizionate nei punti x1,y1, x2,y2, …, posto
# m = c(m1,m2,…), x = c(x1,x2,…), y = c(y1,y2,…), le coordinate del baricentro sono:
sum(m*x)/sum(m); sum(m*y)/sum(m)
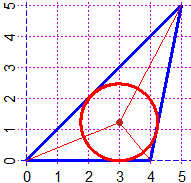
# Il comando incentro traccia il centro del cerchio
# inscritto in un triangolo (l'incentro del triangolo).
# Un esempio:
PIANO(0,5, 0,5); x=c(0,4,5,0); y=c(0,0,5,0)
C = incentro(x,y); spezzata(x,y,"blue")
POINT(C[1],C[2],"brown")
cerchio(C[1],C[2], C[2], "red")
linea(0,0,C[1],C[2],"red")
linea(4,0,C[1],C[2],"red")
linea(5,5,C[1],C[2],"red")
|
 |
# 26 Orologi e pause
Ore(), Minuti(), Secondi() forniscono informazioni sull'ora.
Sec() n. di sec. trascorsi da avvio del programma (utile per animazioni).
attendi(x) fa trascorrere x secondi (utile per animazioni) (vedi 25 e 27)
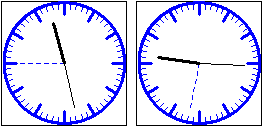
orologio() visualizza un orologio attuale per 10 secondi e stampa l'ora.
orologio2(h,m,s) visualizza un orologio con l'ora indicata
orologio()
orologio2(21,15,32)
 # 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
Puoi tracciare curve in forma parametrica battendo:
param(X,Y, a,b, col) se hai già definito 2 funz. X e Y di un parametro
che varia tra a e b, o in forma polare con:
polar(R, a,b, col) se hai def. R funz. dell'angolo tra a e b.
Es.: le seguenti istruzioni tracciano un'ellisse:
PIANO(-2,2,-2,2)
f <- function(t) 2*cos(t); g <- function(t) sin(t); param(f,g,0,2*pi,'red')
e queste una spirale
PIANO(-5,5,-5,5); r <- function(a) sqrt(a); polar(r,0,20,'blue')
Con para() par1() pola() pol1() si ha uno spessore minore
paramb, polarb, …, pol1b scelgono anche il box, monometrico
Per rototraslare la curva K(x,y)=0 di un angolo di A° attorno all'origine e
un vettore (h,k) e dilatarla orizzontalm. e vert. dei fattori mx e my usa:
rottramol(K, A, h,k, mx,my, col)
rottramo(..) rottram(..) come rotramol di spessore minore
rottra(K, A, h,k, col) si limita a rototraslarla
Per dilatarla e traslarla e, infine, ruotarla attorno all'origine:
moltrarot(K, mx,my, h,k, A, col) moltraro(..) moltrar(..)
moltra(K, mx,my, h,k, col) si limita a dilatarla e traslarla
trasla(K, h,k, col) a traslarla
moltiplica(K, mx,my, col) a dilatarla
Ad ogni trasformazione l'equazione della curva trasformata viene memorizzata nella
variabile ZZZ che, volendo, può essere memorizzata con un altro nome e, poi, eventual-
mente sottoposta ad altre trasformazioni. Per non visualizzare una curva intermedia le
diamo il colore -1 (col colore 0 viene tratteggiata).
Esempi - 27
# 28 Calcoli tra interi comunque grandi. Stringhe <-> Numeri Basi ≠ dieci
Se metti ad es. in x e y due interi ≥ 0 comunque grandi con som(x,y) e pro(x,y)
ne hai somma e prodotto. Se z è un altro intero ottieni ad es. (x*y)*(x+z) con
pro( pro(x,y), som(x,z) )
dif(x,y) calcola la differenza non negativa: x-y se x>=y, 0 altrimenti,
app(x) trasforma la stringa di numeri in un numero approssimato
[se un numero ha più di 17 cifre devi metterlo tra "]
Le stringhe sono delle sequenze di caratteri, racchiuse tra virgolette (" o '). Se
una stringa è formata solo da cifre posso trasformarla in un numero intero col comando
strtoi. Posso calcolare il numero dei caratteri di una stringa con nchar, estrarne una
sottostringa con substr. Posso invece trasformare un numero in stringa con toString, ma
conviene usare NUMERO che non mette le virgolette: NUMERO(3*2) è 6 inteso come stringa.
Per incollare ("paste") stringhe S,T,… con niente in mezzo uso paste0(S,T,…).
Per trasformare un numero intero N in notazione romana usa as.roman(N).
Per eprimere un rapporto M/N (M, N interi, M<N) in base B visualizzandone C cifre usa
MNB(M,N, B, C)
Esempi - 28
# 29 Disequazioni
diseq(F,G, h,k, colore) punteggia lo spazio tra i grafici di F e di
G [F(x) < G(x)] e le rette verticali di ascisse h e k nel colore scelto.
Ripeti eventualmente il comando per avere più punti.
diseq1(F, k, colore) punteggia dove la f. di 2 variabili F
è minore di k
diseq2(F, k, colore) punteggia dove la f. di 2 variabili F
è maggiore di k
Posso risolvere anche sistemi di disequazioni
Esempi - 29
# 30 Curve al variare dei parametri
Grafici di funzioni e curve al variare di parametri:
In (a,b)×(c,d), al variare di u,v,w
fun3p(f, a,b,c,d) polar3p(R, t1,t2, a,b,c,d)
In (a,b)×(c,d), al variare di u,v,w,k
curva4p(F, a,b,c,d)
Vedi gli esempi
Esempi - 30
# 31 Punti dotati di precisione. Retta approssimante
Rette che passano esattamente per (A,B) e passano per i punti di ascisse x e ordinate
y con le precisioni ex ed ey. Comando:
puntiapp(A,B, x,y, ex,ey)
puntiapp2(A,B, x,y, ex,ey) produce le uscite in forma frazionaria
Se invece uso il seguente comando rappresento i punti senza curve che li approssimino
puntiapp0(x,y, ex,ey)
# Posso cambiare colore ai rettangolini che rappresentano i punti col comando colRet
Esempi - 31
# 32 Risoluzione di sistemi lineari e di sistemi in due incognite
sistema(x) risolve il sistema lineare x
soluzione[n] è la soluzione n-esima (se prima di "sistema" metto noStampa=1 le
soluzioni non vengono stampate e le posso vedere solo col comando soluzione).
Vedi gli esempi per la risoluzione di altri sistemi
Esempi - 32
# 33 Pendenza di un grafico
Definisci una funz. f (o g, h1, …). Dando il comando seguente hai il grafico di f per
input tra a e b, output tra c e d, con evidenziato (x0,f(x0)). Se clicchi in un punto
hai il grafico della retta che passa per i punti del grafico di ascissa x0 e di quella
cliccata. Se clicchi l'ascissa x0 hai la retta tangente.
Premi in alto a sinistra per finire.
Comando: pend(f, a,b, c,d, x0)
Prova con: h <- function(x) x^2; pend(h, -1,1.5, 0,3, 1)
Esempi - 33
# 34 Calcolo vettor., differenz. e integrale, lunghezze ed aree
# (e num. complessi, matrici, limiti, serie)
prodv(x,y), prods(x,y), modulo(x), versore(x)
areaF(f, a,b, N) (o areaFun) calcola l'area dell'N-agono che approssima il grafico di f.
L'area del poligono che sta sotto al grafico di una funzione per punti, di coordinate
in x e y, posso calcolarla usando il comando areaPol, definendo la funzione
integr = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
areaPar(x,y, a,b, N), areaPolar(r, a,b, N) calcolano quella racchiusa da una curva in
forma parametrica e in forma polare (vedi 27 e 30). Per calcolare la lunghezza (quando
è finita) di una curva si usano lungFun(f,a,b,N), lungPar(x,y,a,b,N), lungPolar(r,a,b,N)
a seconda di come è definita. lungPar3(x,y,z,a,b,N) opera analogamente per una curva
nello spazio. Vedi qui per aree racchiuse da curve esprimibili solo in forma cartesiana.
derivata(f,NomeVariabile), derivata2,…,derivata6, integrale(f,a,b)
Se F è una fun. di almeno 2 variabili, se due di queste sono u e v, derivataxy(f,u,v)
calcola la derivata parziale seconda rispetto ad u e v, derivatayx(f,u,v) quella
rispetto a v e u (xy e yx indicano che le derivate sono "incrociate", anche se le var.
non sono x e y).
Grafico della funz. integrale: gintegrale(f,A,B,col), grafico del valore dell'integrale
da A ad x per x che varia tra A e B; gintegral, gintegra grafici più sottili.
Data una funzione F di x e di y, hessiano(F,a,b) calcola l'hessiano di F in (a,b).
Per operare con i numeri complessi e con le matrici rinviamo alla guida per l'uso
di R, qui (clicca le rispettive voci) e agli esercizi qui e qui. Lo stesso facciamo
per le funzioni di più variabili: vedi.
Per limiti e serie (anche di Fourier) vedi qui.
Esempi - 34
# 35 Immagini date le coordinate
Per caricare immagini di cui siano memorizzate le coordinate posso ricorrere
ai comandi xTab(D) e yTab(D) se in D c'è la collezione delle coordinate
x1,y1, x2,y2, ..., xN,yN. Ci sono anche appositi comandi per le tabelle.
Esempi - 35
# 36 Regressione, spline
Regressione lineare, quadratica e cubica: la funzione lineare con grafico
per un punto dato (p,q) e le generiche funzioni lineare, quadratica e cubica
che "meglio" approssimano alcuni dati sperimentali (x,y). Comandi:
regressione(x,y,p,q), regressione1(x,y), regressione2(x,y), regressione3(x,y)
Se i punti sono 2, 3 o 4 regressione1, regressione2 e regressione3 trovano
esattamente la curva. Negli es. è richiamato anche il calcolo delle spline.
Esempi - 36
# 37 Curve di Bezier
Puoi tracciare curve introducendo punti che ne guidino l'andamento
(metodo di Bezier). Messe le coordinate in X e Y, scelta una scala, usa
bezier(X,Y,N) dove N è 0 o un codice colore. Prova con
bezier(a,b,1) bezier(a,b,0) bezier(a,b,8) dopo aver introdotto:
a <- c(-3,2,2,-1); b <- c(2,2,-2,1); box(-3,3, -3,3)
Esempi - 37
# 38 Grafici multipli
C'è la possibilità di avere più grafici in un'unica finestra,
se via via i box sono introdotti con Bo…, usando i comandi:
rigcol(m,n) o colrig(n,m)
Esempi - 38
# 39 Equazioni differenziali
Soluzione di equazioni differenziali del 1° ordine e tracciamento del campo
direzionale coi comandi soledif(x0,y0, xf, N, col) e diredif(a,b,c,d, m,n)
Esempi - 39
# 40 Prospettiva
Esempi di visioni in prospettiva (vedi la guida ad R per approfondimenti).
Comandi: casa() GRAF3D() BOH() seba(0) seba(1)
( premi INVIO per far partire i programmi, dopo averli caricati )
Esempi - 40
# 41 Lancio di dadi
Lancio di dadi: Dado(n), DadoB(n)
# 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
Puoi tracciare curve in forma parametrica battendo:
param(X,Y, a,b, col) se hai già definito 2 funz. X e Y di un parametro
che varia tra a e b, o in forma polare con:
polar(R, a,b, col) se hai def. R funz. dell'angolo tra a e b.
Es.: le seguenti istruzioni tracciano un'ellisse:
PIANO(-2,2,-2,2)
f <- function(t) 2*cos(t); g <- function(t) sin(t); param(f,g,0,2*pi,'red')
e queste una spirale
PIANO(-5,5,-5,5); r <- function(a) sqrt(a); polar(r,0,20,'blue')
Con para() par1() pola() pol1() si ha uno spessore minore
paramb, polarb, …, pol1b scelgono anche il box, monometrico
Per rototraslare la curva K(x,y)=0 di un angolo di A° attorno all'origine e
un vettore (h,k) e dilatarla orizzontalm. e vert. dei fattori mx e my usa:
rottramol(K, A, h,k, mx,my, col)
rottramo(..) rottram(..) come rotramol di spessore minore
rottra(K, A, h,k, col) si limita a rototraslarla
Per dilatarla e traslarla e, infine, ruotarla attorno all'origine:
moltrarot(K, mx,my, h,k, A, col) moltraro(..) moltrar(..)
moltra(K, mx,my, h,k, col) si limita a dilatarla e traslarla
trasla(K, h,k, col) a traslarla
moltiplica(K, mx,my, col) a dilatarla
Ad ogni trasformazione l'equazione della curva trasformata viene memorizzata nella
variabile ZZZ che, volendo, può essere memorizzata con un altro nome e, poi, eventual-
mente sottoposta ad altre trasformazioni. Per non visualizzare una curva intermedia le
diamo il colore -1 (col colore 0 viene tratteggiata).
Esempi - 27
# 28 Calcoli tra interi comunque grandi. Stringhe <-> Numeri Basi ≠ dieci
Se metti ad es. in x e y due interi ≥ 0 comunque grandi con som(x,y) e pro(x,y)
ne hai somma e prodotto. Se z è un altro intero ottieni ad es. (x*y)*(x+z) con
pro( pro(x,y), som(x,z) )
dif(x,y) calcola la differenza non negativa: x-y se x>=y, 0 altrimenti,
app(x) trasforma la stringa di numeri in un numero approssimato
[se un numero ha più di 17 cifre devi metterlo tra "]
Le stringhe sono delle sequenze di caratteri, racchiuse tra virgolette (" o '). Se
una stringa è formata solo da cifre posso trasformarla in un numero intero col comando
strtoi. Posso calcolare il numero dei caratteri di una stringa con nchar, estrarne una
sottostringa con substr. Posso invece trasformare un numero in stringa con toString, ma
conviene usare NUMERO che non mette le virgolette: NUMERO(3*2) è 6 inteso come stringa.
Per incollare ("paste") stringhe S,T,… con niente in mezzo uso paste0(S,T,…).
Per trasformare un numero intero N in notazione romana usa as.roman(N).
Per eprimere un rapporto M/N (M, N interi, M<N) in base B visualizzandone C cifre usa
MNB(M,N, B, C)
Esempi - 28
# 29 Disequazioni
diseq(F,G, h,k, colore) punteggia lo spazio tra i grafici di F e di
G [F(x) < G(x)] e le rette verticali di ascisse h e k nel colore scelto.
Ripeti eventualmente il comando per avere più punti.
diseq1(F, k, colore) punteggia dove la f. di 2 variabili F
è minore di k
diseq2(F, k, colore) punteggia dove la f. di 2 variabili F
è maggiore di k
Posso risolvere anche sistemi di disequazioni
Esempi - 29
# 30 Curve al variare dei parametri
Grafici di funzioni e curve al variare di parametri:
In (a,b)×(c,d), al variare di u,v,w
fun3p(f, a,b,c,d) polar3p(R, t1,t2, a,b,c,d)
In (a,b)×(c,d), al variare di u,v,w,k
curva4p(F, a,b,c,d)
Vedi gli esempi
Esempi - 30
# 31 Punti dotati di precisione. Retta approssimante
Rette che passano esattamente per (A,B) e passano per i punti di ascisse x e ordinate
y con le precisioni ex ed ey. Comando:
puntiapp(A,B, x,y, ex,ey)
puntiapp2(A,B, x,y, ex,ey) produce le uscite in forma frazionaria
Se invece uso il seguente comando rappresento i punti senza curve che li approssimino
puntiapp0(x,y, ex,ey)
# Posso cambiare colore ai rettangolini che rappresentano i punti col comando colRet
Esempi - 31
# 32 Risoluzione di sistemi lineari e di sistemi in due incognite
sistema(x) risolve il sistema lineare x
soluzione[n] è la soluzione n-esima (se prima di "sistema" metto noStampa=1 le
soluzioni non vengono stampate e le posso vedere solo col comando soluzione).
Vedi gli esempi per la risoluzione di altri sistemi
Esempi - 32
# 33 Pendenza di un grafico
Definisci una funz. f (o g, h1, …). Dando il comando seguente hai il grafico di f per
input tra a e b, output tra c e d, con evidenziato (x0,f(x0)). Se clicchi in un punto
hai il grafico della retta che passa per i punti del grafico di ascissa x0 e di quella
cliccata. Se clicchi l'ascissa x0 hai la retta tangente.
Premi in alto a sinistra per finire.
Comando: pend(f, a,b, c,d, x0)
Prova con: h <- function(x) x^2; pend(h, -1,1.5, 0,3, 1)
Esempi - 33
# 34 Calcolo vettor., differenz. e integrale, lunghezze ed aree
# (e num. complessi, matrici, limiti, serie)
prodv(x,y), prods(x,y), modulo(x), versore(x)
areaF(f, a,b, N) (o areaFun) calcola l'area dell'N-agono che approssima il grafico di f.
L'area del poligono che sta sotto al grafico di una funzione per punti, di coordinate
in x e y, posso calcolarla usando il comando areaPol, definendo la funzione
integr = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
areaPar(x,y, a,b, N), areaPolar(r, a,b, N) calcolano quella racchiusa da una curva in
forma parametrica e in forma polare (vedi 27 e 30). Per calcolare la lunghezza (quando
è finita) di una curva si usano lungFun(f,a,b,N), lungPar(x,y,a,b,N), lungPolar(r,a,b,N)
a seconda di come è definita. lungPar3(x,y,z,a,b,N) opera analogamente per una curva
nello spazio. Vedi qui per aree racchiuse da curve esprimibili solo in forma cartesiana.
derivata(f,NomeVariabile), derivata2,…,derivata6, integrale(f,a,b)
Se F è una fun. di almeno 2 variabili, se due di queste sono u e v, derivataxy(f,u,v)
calcola la derivata parziale seconda rispetto ad u e v, derivatayx(f,u,v) quella
rispetto a v e u (xy e yx indicano che le derivate sono "incrociate", anche se le var.
non sono x e y).
Grafico della funz. integrale: gintegrale(f,A,B,col), grafico del valore dell'integrale
da A ad x per x che varia tra A e B; gintegral, gintegra grafici più sottili.
Data una funzione F di x e di y, hessiano(F,a,b) calcola l'hessiano di F in (a,b).
Per operare con i numeri complessi e con le matrici rinviamo alla guida per l'uso
di R, qui (clicca le rispettive voci) e agli esercizi qui e qui. Lo stesso facciamo
per le funzioni di più variabili: vedi.
Per limiti e serie (anche di Fourier) vedi qui.
Esempi - 34
# 35 Immagini date le coordinate
Per caricare immagini di cui siano memorizzate le coordinate posso ricorrere
ai comandi xTab(D) e yTab(D) se in D c'è la collezione delle coordinate
x1,y1, x2,y2, ..., xN,yN. Ci sono anche appositi comandi per le tabelle.
Esempi - 35
# 36 Regressione, spline
Regressione lineare, quadratica e cubica: la funzione lineare con grafico
per un punto dato (p,q) e le generiche funzioni lineare, quadratica e cubica
che "meglio" approssimano alcuni dati sperimentali (x,y). Comandi:
regressione(x,y,p,q), regressione1(x,y), regressione2(x,y), regressione3(x,y)
Se i punti sono 2, 3 o 4 regressione1, regressione2 e regressione3 trovano
esattamente la curva. Negli es. è richiamato anche il calcolo delle spline.
Esempi - 36
# 37 Curve di Bezier
Puoi tracciare curve introducendo punti che ne guidino l'andamento
(metodo di Bezier). Messe le coordinate in X e Y, scelta una scala, usa
bezier(X,Y,N) dove N è 0 o un codice colore. Prova con
bezier(a,b,1) bezier(a,b,0) bezier(a,b,8) dopo aver introdotto:
a <- c(-3,2,2,-1); b <- c(2,2,-2,1); box(-3,3, -3,3)
Esempi - 37
# 38 Grafici multipli
C'è la possibilità di avere più grafici in un'unica finestra,
se via via i box sono introdotti con Bo…, usando i comandi:
rigcol(m,n) o colrig(n,m)
Esempi - 38
# 39 Equazioni differenziali
Soluzione di equazioni differenziali del 1° ordine e tracciamento del campo
direzionale coi comandi soledif(x0,y0, xf, N, col) e diredif(a,b,c,d, m,n)
Esempi - 39
# 40 Prospettiva
Esempi di visioni in prospettiva (vedi la guida ad R per approfondimenti).
Comandi: casa() GRAF3D() BOH() seba(0) seba(1)
( premi INVIO per far partire i programmi, dopo averli caricati )
Esempi - 40
# 41 Lancio di dadi
Lancio di dadi: Dado(n), DadoB(n)
 Esempi - 41
# 42 Escher
Tassellazioni di Escher: escher()
Esempi - 42
# 43 Struttura dei termini
Visalizzazione della struttura dei termini
Esempi - 43
# 44 Grafi ad albero
Esempi - 44
# 45 Altre immagini
Esempi - 45
Oltre alle immagini animate come quelle viste in 25 e 27, si possono costruire
file html animati come questo nel modo spiegato qui. Per scaricare la cartella
contenente l'esempio e le spiegazioni clicca qui.
------------------------------------------------------------------
Esempi - 27 (vedi)
PIANO(-60,60, -60,60)
ro1 <- function(a) a^1.5
polar(ro1,0,5*pi, "red")
ro2 <- function(a) 30/(2+sin(a)-cos(a))
polar(ro2,0,5*pi, "green")
asc1 <- function(t) 2*t^2-3*t
ord1 <- function(t) t^3-t+1
param(asc1, ord1, -10,10, "blue")
asc2 <- function(t) -30+20*cos(t)
ord2 <- function(t) 10+30*sin(t)
param(asc2, ord2, 0,2*pi, "magenta")
H <- function(x,y) x*y-100
curva(H, "grey")
rottramo(H, 45, 0,0, 1.5,1, "black")
#
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, "blue")
punto(4,3, "red"); moltrarot(F, 8,4, 4,3, -30, "blue")
# figura a destra:
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, -1); C1 = ZZZ
PUNTO(4,3, "magenta"); moltrarot(F, 8,4, 4,3, -30, "blue")
moltrarot(C1, 1,1, 0,2, 0, "red"); moltrarot(C1, 1/2,1/2, 0,2, 0, "grey")
( in "polar" è inteso che l'ang. è in radianti; per fare il grafico di ro(a) con
a in gradi tra h e k fai quello di ro1(x) = ro(x/gradi) tra h/gradi e k/gradi )
# Come costruire un'immagine animata (vedi a metà del punto 25):
# La costruzione di un asteroide (la figura tracciata da un punto
# di un cerchio che ruota su un cerchio maggiore)
PIANO(-4,4, -4,4)
f <- function(t) 4*cos(t)^3; g <- function(t) 4*sin(t)^3
cerchio(0,0, 4, "grey"); param(f,g, 0,2*pi, "grey"); fig0 <- fig <- recordPlot()
i <- 0; x <- 4; y <- 0; dt <- 0.3
while(i < 90) {replayPlot(fig); PUNTI(x,y,"brown"); fig <- recordPlot()
i <- i+1
t <- 2*pi/90*i; cerchio(3*cos(t),3*sin(t), 1, "red");
freccia(3*cos(t),3*sin(t), 4*cos(t)^3, 4*sin(t)^3, "blue");
x <- c(x,4*cos(t)^3); y <- c(y,4*sin(t)^3); attendi(dt) }
attendi(dt); replayPlot(fig0); param(f,g, 0,2*pi, "brown")
# Per una versione senza "griglia" clicca qui.
Esempi - 41
# 42 Escher
Tassellazioni di Escher: escher()
Esempi - 42
# 43 Struttura dei termini
Visalizzazione della struttura dei termini
Esempi - 43
# 44 Grafi ad albero
Esempi - 44
# 45 Altre immagini
Esempi - 45
Oltre alle immagini animate come quelle viste in 25 e 27, si possono costruire
file html animati come questo nel modo spiegato qui. Per scaricare la cartella
contenente l'esempio e le spiegazioni clicca qui.
------------------------------------------------------------------
Esempi - 27 (vedi)
PIANO(-60,60, -60,60)
ro1 <- function(a) a^1.5
polar(ro1,0,5*pi, "red")
ro2 <- function(a) 30/(2+sin(a)-cos(a))
polar(ro2,0,5*pi, "green")
asc1 <- function(t) 2*t^2-3*t
ord1 <- function(t) t^3-t+1
param(asc1, ord1, -10,10, "blue")
asc2 <- function(t) -30+20*cos(t)
ord2 <- function(t) 10+30*sin(t)
param(asc2, ord2, 0,2*pi, "magenta")
H <- function(x,y) x*y-100
curva(H, "grey")
rottramo(H, 45, 0,0, 1.5,1, "black")
#
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, "blue")
punto(4,3, "red"); moltrarot(F, 8,4, 4,3, -30, "blue")
# figura a destra:
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, -1); C1 = ZZZ
PUNTO(4,3, "magenta"); moltrarot(F, 8,4, 4,3, -30, "blue")
moltrarot(C1, 1,1, 0,2, 0, "red"); moltrarot(C1, 1/2,1/2, 0,2, 0, "grey")
( in "polar" è inteso che l'ang. è in radianti; per fare il grafico di ro(a) con
a in gradi tra h e k fai quello di ro1(x) = ro(x/gradi) tra h/gradi e k/gradi )
# Come costruire un'immagine animata (vedi a metà del punto 25):
# La costruzione di un asteroide (la figura tracciata da un punto
# di un cerchio che ruota su un cerchio maggiore)
PIANO(-4,4, -4,4)
f <- function(t) 4*cos(t)^3; g <- function(t) 4*sin(t)^3
cerchio(0,0, 4, "grey"); param(f,g, 0,2*pi, "grey"); fig0 <- fig <- recordPlot()
i <- 0; x <- 4; y <- 0; dt <- 0.3
while(i < 90) {replayPlot(fig); PUNTI(x,y,"brown"); fig <- recordPlot()
i <- i+1
t <- 2*pi/90*i; cerchio(3*cos(t),3*sin(t), 1, "red");
freccia(3*cos(t),3*sin(t), 4*cos(t)^3, 4*sin(t)^3, "blue");
x <- c(x,4*cos(t)^3); y <- c(y,4*sin(t)^3); attendi(dt) }
attendi(dt); replayPlot(fig0); param(f,g, 0,2*pi, "brown")
# Per una versione senza "griglia" clicca qui.
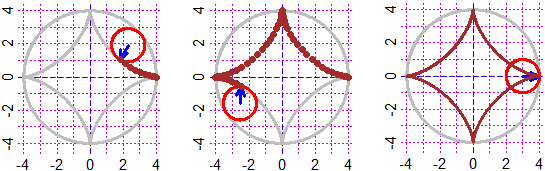 Esempi - 28 (vedi)
## Il calcolo di x*(10+x)+5*x^3 per x=123456789012345
x <- "123456789012345"
som( pro(x, som(10,x)), pro(5, pro(x, pro(x,x))))
# "9408381861768148891412848380186556157340600"
## Verifica. Batto il numero e ottengo la rappr. esponenziale:
9408381861768148891412848380186556157340600
# 9.408382e+42
## Cosa otterremmo direttamente:
x <- 123456789012345; x*(10+x)+5*x^3; piu(ultimo())
# 9.408382e+42 9.40838186176815e+42
#
## 40!
n <- 40; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "815915283247897734345611269596115894272000000000"
## 171!
n <- 171; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "1241018070217667823424840524103103992616605577501693185388951803
6119960752216917529927519781204875855764649595016703870528098898
5869071076733124203221848436431047357788996854827829075454156196
4852153468318044293239598173696899657235903947616152278558180061
176365108428800000000000000000000000000000000000000000"
## Un trucco per stampare una stringa lunga su più righe:
str <- z; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "12410180702176678234248405241031039926166055775016931853889518036119960752216917"
# "52992751978120487585576464959501670387052809889858690710767331242032218484364310"
# "47357788996854827829075454156196485215346831804429323959817369689965723590394761"
# "6152278558180061176365108428800000000000000000000000000000000000000000"
#
## 2^1024, non calcolabile direttamente
2^1023; 2^1024
# 8.988466e+307 Inf
## Col programma per 2^1024 ottengo:
y <- 1; for(i in 1:1024) y <- pro(y,2)
str <- y; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "17976931348623159077293051907890247336179769789423065727343008115773267580550096"
"31327084773224075360211201138798713933576587897688144166224928474306394741243777"
"67893424865485276302219601246094119453082952085005768838150682342462881473913110"
"7237163350510684586298239947245938479716304835356329624224137216"
## nchar(y) -> 309 Sono 309 cifre (quelle di 2^1023 erano 308)
#
## Approssimazione in notazione scientifica
x <- "12345678901234567890"; app(x)
# 1.234568e+19
#
## 1000^20-999^20
y <- 1; for(i in 1:20) y <- pro(y,999)
z <- 1; for(i in 1:20) z <- pro(z,1000)
dif(z,y)
# "19811135170465317394197775411834107481255499156139810019999"
app(z); app(y); app(dif(z,y))
# 1e+60 9.801889e+59 1.981114e+58
#
## Stringhe <-> Numeri
N <- NUMERO(137); S <- substr(N,2,3); S; nchar(S); strtoi(paste0(S,"0",S))
# "37" 2 37037
## Numeri romani
as.roman(1944)
# MCMXLIV
## Rapporti < 1 in basi varie (4/100 in base 2, 55 cifre)
MNB(4,100, 2,55)
# 0. 0 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0
# 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 resto 36
Esempi - 29 (vedi)
F <- function(x) x*(x-2); G <- function(x) x/2
graficoF(F,-1,3, "blue"); grafico(G,-1,3, "red")
# vedi i grafici sotto a sinistra
diseq(F,G,-1,3,"black")
diseq(F,G,-1,3,"black")
diseq(G,F,-1,3,"orange")
diseq(G,F,-1,3,"orange")
Esempi - 28 (vedi)
## Il calcolo di x*(10+x)+5*x^3 per x=123456789012345
x <- "123456789012345"
som( pro(x, som(10,x)), pro(5, pro(x, pro(x,x))))
# "9408381861768148891412848380186556157340600"
## Verifica. Batto il numero e ottengo la rappr. esponenziale:
9408381861768148891412848380186556157340600
# 9.408382e+42
## Cosa otterremmo direttamente:
x <- 123456789012345; x*(10+x)+5*x^3; piu(ultimo())
# 9.408382e+42 9.40838186176815e+42
#
## 40!
n <- 40; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "815915283247897734345611269596115894272000000000"
## 171!
n <- 171; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "1241018070217667823424840524103103992616605577501693185388951803
6119960752216917529927519781204875855764649595016703870528098898
5869071076733124203221848436431047357788996854827829075454156196
4852153468318044293239598173696899657235903947616152278558180061
176365108428800000000000000000000000000000000000000000"
## Un trucco per stampare una stringa lunga su più righe:
str <- z; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "12410180702176678234248405241031039926166055775016931853889518036119960752216917"
# "52992751978120487585576464959501670387052809889858690710767331242032218484364310"
# "47357788996854827829075454156196485215346831804429323959817369689965723590394761"
# "6152278558180061176365108428800000000000000000000000000000000000000000"
#
## 2^1024, non calcolabile direttamente
2^1023; 2^1024
# 8.988466e+307 Inf
## Col programma per 2^1024 ottengo:
y <- 1; for(i in 1:1024) y <- pro(y,2)
str <- y; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "17976931348623159077293051907890247336179769789423065727343008115773267580550096"
"31327084773224075360211201138798713933576587897688144166224928474306394741243777"
"67893424865485276302219601246094119453082952085005768838150682342462881473913110"
"7237163350510684586298239947245938479716304835356329624224137216"
## nchar(y) -> 309 Sono 309 cifre (quelle di 2^1023 erano 308)
#
## Approssimazione in notazione scientifica
x <- "12345678901234567890"; app(x)
# 1.234568e+19
#
## 1000^20-999^20
y <- 1; for(i in 1:20) y <- pro(y,999)
z <- 1; for(i in 1:20) z <- pro(z,1000)
dif(z,y)
# "19811135170465317394197775411834107481255499156139810019999"
app(z); app(y); app(dif(z,y))
# 1e+60 9.801889e+59 1.981114e+58
#
## Stringhe <-> Numeri
N <- NUMERO(137); S <- substr(N,2,3); S; nchar(S); strtoi(paste0(S,"0",S))
# "37" 2 37037
## Numeri romani
as.roman(1944)
# MCMXLIV
## Rapporti < 1 in basi varie (4/100 in base 2, 55 cifre)
MNB(4,100, 2,55)
# 0. 0 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0
# 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 resto 36
Esempi - 29 (vedi)
F <- function(x) x*(x-2); G <- function(x) x/2
graficoF(F,-1,3, "blue"); grafico(G,-1,3, "red")
# vedi i grafici sotto a sinistra
diseq(F,G,-1,3,"black")
diseq(F,G,-1,3,"black")
diseq(G,F,-1,3,"orange")
diseq(G,F,-1,3,"orange")
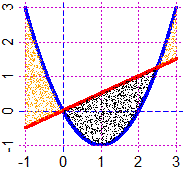
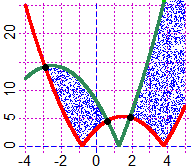 # Per il grafico a destra ( |x^2-3*x-3| < |x^2+5*x-8| ) vedi qui.
k <- function(x,y) abs(x)+abs(y)-1
PIANO(-2,2, -2,2); curva(k,"blue"); diseq1(k,0,"red")
#
h <- function(x,y) (x-1)^2+0.5*(y+3)^2
# dove h < 2 e dove h > 3
PIANO(-3,3, -6,0)
diseq1(h,2, "blue"); diseq1(h,2, "blue")
diseq2(h,3, "red"); diseq2(h,3, "red")
#
P <- function(x,y) x >= y & x-y <=1 & 0 <= x & x <= 1
# dove P è vera (val. 1) e dove è falsa (val. 0)
PIANO(-2,2, -2,2)
diseq1(P,1,"blue"); diseq1(P,1,"blue") # falsa
diseq2(P,0, "red"); diseq2(P,0, "red") # vera
for(i in 1:10) diseq1(P,1,"blue"); for(i in 1:10) diseq2(P,0,"red")
# Per il grafico a destra ( |x^2-3*x-3| < |x^2+5*x-8| ) vedi qui.
k <- function(x,y) abs(x)+abs(y)-1
PIANO(-2,2, -2,2); curva(k,"blue"); diseq1(k,0,"red")
#
h <- function(x,y) (x-1)^2+0.5*(y+3)^2
# dove h < 2 e dove h > 3
PIANO(-3,3, -6,0)
diseq1(h,2, "blue"); diseq1(h,2, "blue")
diseq2(h,3, "red"); diseq2(h,3, "red")
#
P <- function(x,y) x >= y & x-y <=1 & 0 <= x & x <= 1
# dove P è vera (val. 1) e dove è falsa (val. 0)
PIANO(-2,2, -2,2)
diseq1(P,1,"blue"); diseq1(P,1,"blue") # falsa
diseq2(P,0, "red"); diseq2(P,0, "red") # vera
for(i in 1:10) diseq1(P,1,"blue"); for(i in 1:10) diseq2(P,0,"red")
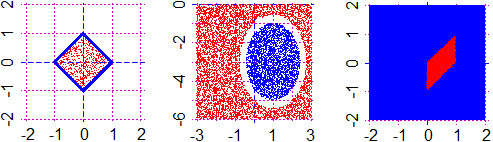 # Attenzione: il software non basta
# Vediamo la risoluzione di 3/(4*x – 5) > 4.
Piano(-5,5, -5,5)
f <- function(x) 3/(4*x-5); g <- function(x) 4
grafico(f,-5,5, 1); grafico(g,-5,5, "red")
# Capisco che le soluzioni sono in un intervallino tra 0 e 2, ma
# per rappresentare la diseq. devo avere un intervallo in cui i due
# grafici non abbiano salti. Dove è il salto? Risolvo l'equazione
# 4*x-5 = 0. È facile, ma vediamo come farlo col computer:
h <- function(x) 4*x-5; soluz(h,0, 0,2)
# 1.25
Piano(0,2,-1,8); grafico(f,0,2, 1); grafico(g,0,2, "red")
diseq(g,f, 1.25,2, "brown"); diseq(g,f, 1.25,2, "brown")
# Attenzione: il software non basta
# Vediamo la risoluzione di 3/(4*x – 5) > 4.
Piano(-5,5, -5,5)
f <- function(x) 3/(4*x-5); g <- function(x) 4
grafico(f,-5,5, 1); grafico(g,-5,5, "red")
# Capisco che le soluzioni sono in un intervallino tra 0 e 2, ma
# per rappresentare la diseq. devo avere un intervallo in cui i due
# grafici non abbiano salti. Dove è il salto? Risolvo l'equazione
# 4*x-5 = 0. È facile, ma vediamo come farlo col computer:
h <- function(x) 4*x-5; soluz(h,0, 0,2)
# 1.25
Piano(0,2,-1,8); grafico(f,0,2, 1); grafico(g,0,2, "red")
diseq(g,f, 1.25,2, "brown"); diseq(g,f, 1.25,2, "brown")
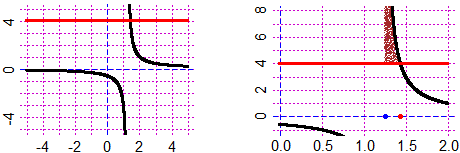 # Ho una conferma grafica: la punteggiatura mostra che la soluzione è l'intervallo
# (1.25,q). Per trovare q tengo conto che le curve si incontrano tra 1.25 e 1.5:
soluz2(f,g, 1.25,1.5)
# 1.4375
# Per avere l'intervallo in forma frazionaria:
frazio(1.25); frazio(1.4375)
# 5/4 23/16
puntino(5/4,0,"blue"); puntino(23/16,0,"red")
Esempi - 30 (vedi)
# Devo usare u,v,w come parametri e du,dv,dw come passi
# Cliccando puoi variare i parametri.
# In grigio viene tracciata la curva precedente.
# Cliccando il bottone blu vedi il grafico più spesso.
# I grafici polari sono in scala monometrica.
# Una parabola in (-5,5)×(-10,10) al variare dei coefficienti
h <- function(x) u*x^2+v*x+w
u <- 1; du <- 0.5; v <- 1; dv <- 1; w <- 0; dw <- 0.5
BF=5; HF=4 # se vuoi aumenta le dimensioni
fun3p(h,-5,5, -10,10)
# Ho una conferma grafica: la punteggiatura mostra che la soluzione è l'intervallo
# (1.25,q). Per trovare q tengo conto che le curve si incontrano tra 1.25 e 1.5:
soluz2(f,g, 1.25,1.5)
# 1.4375
# Per avere l'intervallo in forma frazionaria:
frazio(1.25); frazio(1.4375)
# 5/4 23/16
puntino(5/4,0,"blue"); puntino(23/16,0,"red")
Esempi - 30 (vedi)
# Devo usare u,v,w come parametri e du,dv,dw come passi
# Cliccando puoi variare i parametri.
# In grigio viene tracciata la curva precedente.
# Cliccando il bottone blu vedi il grafico più spesso.
# I grafici polari sono in scala monometrica.
# Una parabola in (-5,5)×(-10,10) al variare dei coefficienti
h <- function(x) u*x^2+v*x+w
u <- 1; du <- 0.5; v <- 1; dv <- 1; w <- 0; dw <- 0.5
BF=5; HF=4 # se vuoi aumenta le dimensioni
fun3p(h,-5,5, -10,10)
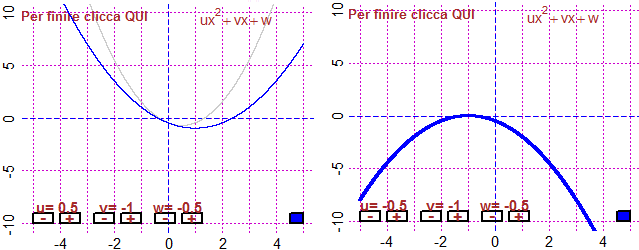 # Questo strumento può essere utile per esplorazioni. Per realizzare fasci di curve è
# più comodo usare direttamente i comandi standard nel modo seguente, ricordando che i
# colori possono essere indicati numericamente:
Ncolori()
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet, 7 yellow, 8 grey
h <- function(x) u*x^2+v*x
Piano(-5,5, -10,10) # grafici sotto a sinistra (v varia da -2 a 5)
u=1; N = c(-2,-1,0,1,2,3,4,5); for(co in 1:8) {v=N[co]; grafi(h,-5,5,co)}
Piano(-5,5, -10,10) # grafici sotto a destra (u varia da -2 a 5)
v=1; N = c(-2,-1,0,1,2,3,4,5); for(co in 1:8) {u=N[co]; grafi(h,-5,5,co)}
# Questo strumento può essere utile per esplorazioni. Per realizzare fasci di curve è
# più comodo usare direttamente i comandi standard nel modo seguente, ricordando che i
# colori possono essere indicati numericamente:
Ncolori()
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet, 7 yellow, 8 grey
h <- function(x) u*x^2+v*x
Piano(-5,5, -10,10) # grafici sotto a sinistra (v varia da -2 a 5)
u=1; N = c(-2,-1,0,1,2,3,4,5); for(co in 1:8) {v=N[co]; grafi(h,-5,5,co)}
Piano(-5,5, -10,10) # grafici sotto a destra (u varia da -2 a 5)
v=1; N = c(-2,-1,0,1,2,3,4,5); for(co in 1:8) {u=N[co]; grafi(h,-5,5,co)}
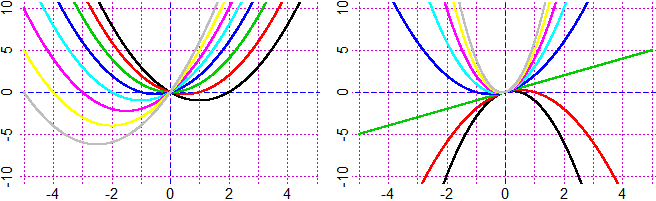 # Nell'esempio che segue uso solo 2 parametri
# Il grafico al variare di t tra 0 e 2π in (-3,9)×(-6,6)
ro <- function(t) u+v*cos(t)
u <- 2; du <- 0.1; v <- 2; dv <- 0.1; w <- 0; dw <- 0
BF=5; HF=4
polar3p(ro, 0,2*pi, -3,9, -6,6)
# Nell'esempio che segue uso solo 2 parametri
# Il grafico al variare di t tra 0 e 2π in (-3,9)×(-6,6)
ro <- function(t) u+v*cos(t)
u <- 2; du <- 0.1; v <- 2; dv <- 0.1; w <- 0; dw <- 0
BF=5; HF=4
polar3p(ro, 0,2*pi, -3,9, -6,6)
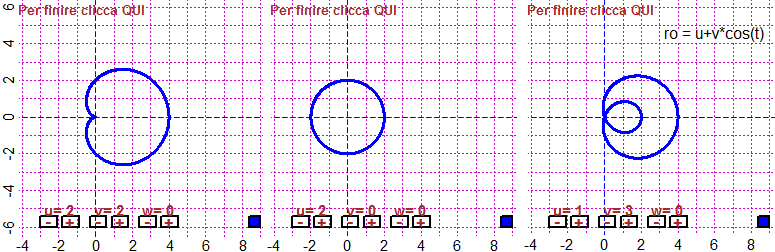 # Volendo tracciare direttamente un fascio di curve:
ro <- function(t) u+v*cos(t)
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet
PIANO(-2,5, -3.5,3.5) # v varia in 0.5 1 1.5 ... 3
u=2; N = c(0.5,1,1.5,2,2.5,3); for(co in 1:6) {v=N[co]; pola(ro, 0,2*pi,co)}
# Volendo tracciare direttamente un fascio di curve:
ro <- function(t) u+v*cos(t)
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet
PIANO(-2,5, -3.5,3.5) # v varia in 0.5 1 1.5 ... 3
u=2; N = c(0.5,1,1.5,2,2.5,3); for(co in 1:6) {v=N[co]; pola(ro, 0,2*pi,co)}
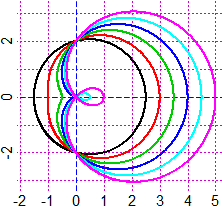 # Per una funz. di 2 var. posso usare anche k e dk.
# Una funz. polinomiale di 2 grado:
u <- 2; du <- 1; v <- 2; dv <- 1; w <- 2; dw <- 1; k <- 2; dk <- 1
G <- function(x,y) x^2*u+y^2*v+w*x - k
BF=5; HF=4
curva4p(G, -3,3, -3,3)
# Per una funz. di 2 var. posso usare anche k e dk.
# Una funz. polinomiale di 2 grado:
u <- 2; du <- 1; v <- 2; dv <- 1; w <- 2; dw <- 1; k <- 2; dk <- 1
G <- function(x,y) x^2*u+y^2*v+w*x - k
BF=5; HF=4
curva4p(G, -3,3, -3,3)
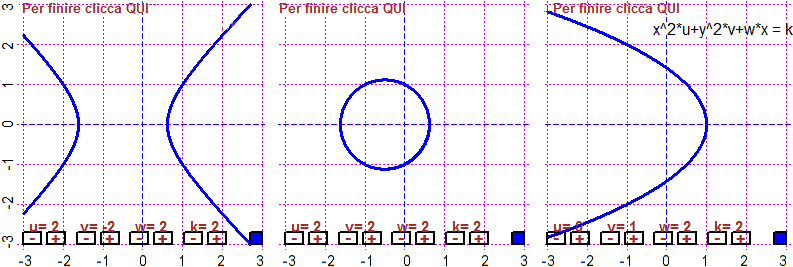 # Volendo tracciare direttamente un fascio di curve:
#1 black, 2 red, 3 green, 4 blue, 5 cyan
BF=4; HF=4
G <- function(x,y) x^2*u+y^2*v+w*x - k
PIANO(-3,3, -3,3) # v varia da -2 a 2
u=2;w=2;k=2; N = c(-2,-1,0,1,2); for(co in 1:5) {v=N[co]; curva(G,co)}
# Volendo tracciare direttamente un fascio di curve:
#1 black, 2 red, 3 green, 4 blue, 5 cyan
BF=4; HF=4
G <- function(x,y) x^2*u+y^2*v+w*x - k
PIANO(-3,3, -3,3) # v varia da -2 a 2
u=2;w=2;k=2; N = c(-2,-1,0,1,2); for(co in 1:5) {v=N[co]; curva(G,co)}
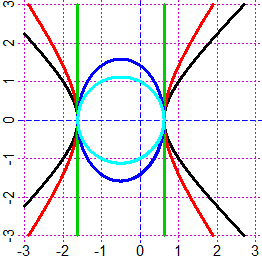 Esempi - 31 (vedi)
# Che cosa posso dire della funzione lineare F tale che F(5) = 10
# il cui grafico passa per i punti dotati di precisione
# x: 12±1 17±1 24±1 33±1.5
# y: 18±2 27±2 31±2.5 45±3
Piano(0,35, 0,50)
x <- c(12, 17, 24, 33); ex <- c(1, 1, 1, 1.5)
y <- c(18, 27, 31, 45); ey <- c(2, 2, 2.5, 3)
puntiapp(5,10, x,y, ex,ey)
# 1.153846 * x + 4.230769 1.153846 * (x - 5 ) + 10
# 1.305556 * x + 3.472222 1.305556 * (x - 5 ) + 10
# Ottengo la figura sottostante a destra:
Esempi - 31 (vedi)
# Che cosa posso dire della funzione lineare F tale che F(5) = 10
# il cui grafico passa per i punti dotati di precisione
# x: 12±1 17±1 24±1 33±1.5
# y: 18±2 27±2 31±2.5 45±3
Piano(0,35, 0,50)
x <- c(12, 17, 24, 33); ex <- c(1, 1, 1, 1.5)
y <- c(18, 27, 31, 45); ey <- c(2, 2, 2.5, 3)
puntiapp(5,10, x,y, ex,ey)
# 1.153846 * x + 4.230769 1.153846 * (x - 5 ) + 10
# 1.305556 * x + 3.472222 1.305556 * (x - 5 ) + 10
# Ottengo la figura sottostante a destra:
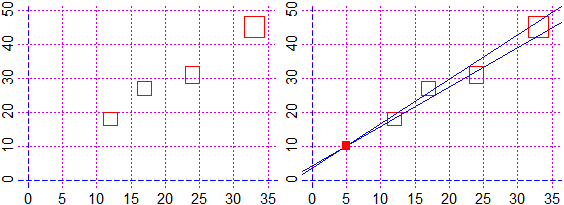 # Se volessi esprimere i valori in forma frazionaria:
puntiapp2(5,10, x,y, ex,ey)
# 15/13 55/13 15/13 5 10 47/36 125/36 47/36 5 10
# deduco: 15/13*x+55/13 15/13*(x-5)+10 47/36*x+125/36 47/36*(x-5)+10
# Se voglio tracciare i punti con le loro precisioni senza approssimarli con una
# retta uso il comando seguente, ottenendo la figura soprastante a sinistra:
puntiapp0(x,y, ex,ey)
# Se prima di questi comandi mettessi ad es. colRet="brown" i rettangolini verrebbero
# tracciati di colore marrone.
# Se le precisioni sono tutte le stesse, se ad es. i punti sono N e ex sono tutte 2,
# posso mettere ex = rep(2,N).
Esempi - 32 (vedi)
## Risolviamo il sistema
# 8x + 7y + 6z = 7.4
# 7x +10y +12z = 8.65
# x + 2y + 4z = 1.75 (vedi qui)
S <- c(8,7,6,7.4, 7,10,12,8.65, 1,2,4,1.75); sistema(S)
# 0.55 0.30 0.15
soluzione[2] # per avere solo la seconda soluzione (y)
# 0.3
# Se il sistema non ha soluzioni o ne ha infinite compare "sistema singolare"
#
# Per i sistemi non lineari si può procedere graficamente e trovare le soluzioni fino
# a 6 o 7 cifre. Ma quando ci si può ricondurre ad un'equazione in una variabile si
# può utilizzare la risoluzione delle equazioni. Vediamo un esempio semplice:
# Trovare le intersezioni tra 2y+3x-15=0 (retta) e (x-3)^2+(y-5)^2=4 (cerchio)
f = function(x) (15-3*x)/2; g = function(x,y) (x-3)^2+(y-5)^2-4
PIANO(0,7, 0,7); curva(g, "blue"); grafico( f, 0,7, "blue")
# ottengo il grafico sotto a sinistra:
# Se volessi esprimere i valori in forma frazionaria:
puntiapp2(5,10, x,y, ex,ey)
# 15/13 55/13 15/13 5 10 47/36 125/36 47/36 5 10
# deduco: 15/13*x+55/13 15/13*(x-5)+10 47/36*x+125/36 47/36*(x-5)+10
# Se voglio tracciare i punti con le loro precisioni senza approssimarli con una
# retta uso il comando seguente, ottenendo la figura soprastante a sinistra:
puntiapp0(x,y, ex,ey)
# Se prima di questi comandi mettessi ad es. colRet="brown" i rettangolini verrebbero
# tracciati di colore marrone.
# Se le precisioni sono tutte le stesse, se ad es. i punti sono N e ex sono tutte 2,
# posso mettere ex = rep(2,N).
Esempi - 32 (vedi)
## Risolviamo il sistema
# 8x + 7y + 6z = 7.4
# 7x +10y +12z = 8.65
# x + 2y + 4z = 1.75 (vedi qui)
S <- c(8,7,6,7.4, 7,10,12,8.65, 1,2,4,1.75); sistema(S)
# 0.55 0.30 0.15
soluzione[2] # per avere solo la seconda soluzione (y)
# 0.3
# Se il sistema non ha soluzioni o ne ha infinite compare "sistema singolare"
#
# Per i sistemi non lineari si può procedere graficamente e trovare le soluzioni fino
# a 6 o 7 cifre. Ma quando ci si può ricondurre ad un'equazione in una variabile si
# può utilizzare la risoluzione delle equazioni. Vediamo un esempio semplice:
# Trovare le intersezioni tra 2y+3x-15=0 (retta) e (x-3)^2+(y-5)^2=4 (cerchio)
f = function(x) (15-3*x)/2; g = function(x,y) (x-3)^2+(y-5)^2-4
PIANO(0,7, 0,7); curva(g, "blue"); grafico( f, 0,7, "blue")
# ottengo il grafico sotto a sinistra:
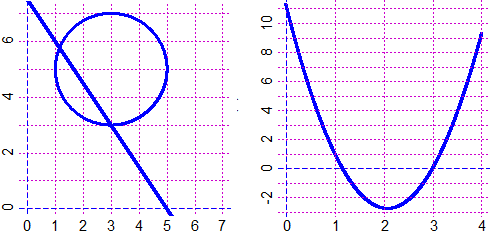 # Per trovare le intersezioni considero:
h = function(x) g(x, f(x)); graficoF( h, -5,5, "blue")
# ottengo il grafico sopra a destra, in cui vedo meglio le "x" soluzioni
soluz(h,0, 0,2)
# 1.153846
piu(soluz(h,0, 0,2))
# 1.15384615384615
frazio(soluz(h,0, 0,2))
# 15/13
soluz(h,0, 2,4)
# 3
# Le x sono 15/13 e 3, trovo le y
f(15/13); f(3)
# 5.769231 3
frazio( f(15/13) )
# 75/13
# Le soluzioni sono (x,y) = (15/13, 75/13) e (x,y) = (3,3), che posso controllare sul
# grafico sopra a sinistra.
Esempi - 33 (vedi)
f <- function(x) cos(x)
pend(f, -3.2,0, -1.6,1.6, -pi/2)
#Nel grafico è segnato un punto P. Cliccando vicino al grafico individua
#una ascissa. Viene tracciata la retta per P e per il punto del grafico
#con tale ascissa. Se vuoi, cliccando, puoi ripetere la prova. Quando
#vuoi finire clicca in alto a sinistra. Ora premi INVIO. 1:
# Per trovare le intersezioni considero:
h = function(x) g(x, f(x)); graficoF( h, -5,5, "blue")
# ottengo il grafico sopra a destra, in cui vedo meglio le "x" soluzioni
soluz(h,0, 0,2)
# 1.153846
piu(soluz(h,0, 0,2))
# 1.15384615384615
frazio(soluz(h,0, 0,2))
# 15/13
soluz(h,0, 2,4)
# 3
# Le x sono 15/13 e 3, trovo le y
f(15/13); f(3)
# 5.769231 3
frazio( f(15/13) )
# 75/13
# Le soluzioni sono (x,y) = (15/13, 75/13) e (x,y) = (3,3), che posso controllare sul
# grafico sopra a sinistra.
Esempi - 33 (vedi)
f <- function(x) cos(x)
pend(f, -3.2,0, -1.6,1.6, -pi/2)
#Nel grafico è segnato un punto P. Cliccando vicino al grafico individua
#una ascissa. Viene tracciata la retta per P e per il punto del grafico
#con tale ascissa. Se vuoi, cliccando, puoi ripetere la prova. Quando
#vuoi finire clicca in alto a sinistra. Ora premi INVIO. 1:
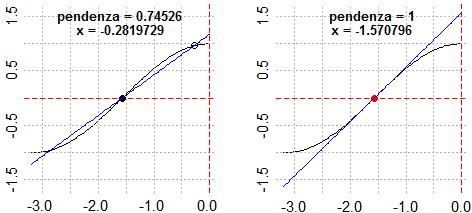 Esempi - 34 (vedi)
# prodotto scalare e (solo nel caso tridimensionale) prodotto vettoriale
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# la somma di vettori si fa col "+" (se li rappresento con freccia, non con Freccia,
# in cui - come abbiamo visto - metto i vettori come dir. e modulo):
v1 <- c(2,3); v2 <- c(-4,1)
PIANO(-4,2, -1,5)
freccia(0,0,v1[1],v1[2], "red")
freccia(0,0,v2[1],v2[2], "blue")
freccia(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
frec(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
frec(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# ricordo che mettere come colore 1 equivale a mettere "black"
Esempi - 34 (vedi)
# prodotto scalare e (solo nel caso tridimensionale) prodotto vettoriale
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# la somma di vettori si fa col "+" (se li rappresento con freccia, non con Freccia,
# in cui - come abbiamo visto - metto i vettori come dir. e modulo):
v1 <- c(2,3); v2 <- c(-4,1)
PIANO(-4,2, -1,5)
freccia(0,0,v1[1],v1[2], "red")
freccia(0,0,v2[1],v2[2], "blue")
freccia(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
frec(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
frec(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# ricordo che mettere come colore 1 equivale a mettere "black"
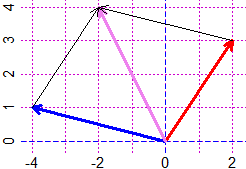 # la direzione e la lunghezza della freccia rossa:
dirFreccia(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# il suo versore e, con un altro comando, la sua lunghezza:
versore(v1); modulo(v1)
# 0.5547002 0.8320503 3.605551
# areaF; esempi per N = 2, 4, 10 mila, 100 mila per una certa f
BF=3; HF=2
f <- function(x) sqrt(1-x^2)
PIANO(-1,1, 0,1); areaF(f,-1,1,2) # 1
PIANO(-1,1, 0,1); areaF(f,-1,1,4) # 1.3660254
PIANO(-1,1, 0,1); areaF(f,-1,1,1e4) # 1.5707947
PIANO(-1,1, 0,1); areaF(f,-1,1,1e5) # 1.5707963 (=π/2)
# la direzione e la lunghezza della freccia rossa:
dirFreccia(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# il suo versore e, con un altro comando, la sua lunghezza:
versore(v1); modulo(v1)
# 0.5547002 0.8320503 3.605551
# areaF; esempi per N = 2, 4, 10 mila, 100 mila per una certa f
BF=3; HF=2
f <- function(x) sqrt(1-x^2)
PIANO(-1,1, 0,1); areaF(f,-1,1,2) # 1
PIANO(-1,1, 0,1); areaF(f,-1,1,4) # 1.3660254
PIANO(-1,1, 0,1); areaF(f,-1,1,1e4) # 1.5707947
PIANO(-1,1, 0,1); areaF(f,-1,1,1e5) # 1.5707963 (=π/2)
 # Usa areaF2 se (per N grande) vuoi un calcolo più veloce
# altro esempio (grafici sotto a sinistra):
Piano(0,3,0,3); areaF(floor, 0,3, 2) # 3.75
Piano(0,3,0,3); areaF(floor, 0,3, 1000) # 3.0015
# Usa areaF2 se (per N grande) vuoi un calcolo più veloce
# altro esempio (grafici sotto a sinistra):
Piano(0,3,0,3); areaF(floor, 0,3, 2) # 3.75
Piano(0,3,0,3); areaF(floor, 0,3, 1000) # 3.0015
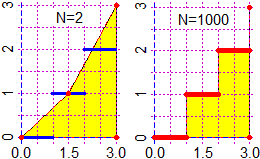
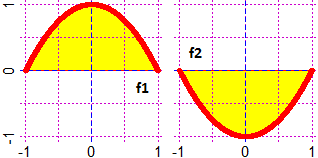 # Le aree sono orientate: positive/negative se stanno sopra/sotto l'asse x
# (figure sopra a destra)
f1 <- function(x) -x^2+1; f2 <- function(x) -f1(x)
BF=3; HF=3
PIANO(-1,1, -1,1); areaF(f1,-1,1,2000) # 1.333333
PIANO(-1,1, -1,1); areaF(f2,-1,1,2000) # -1.333333
# Calcolando opportuni integrali (vedi sotto) posso calcolare facilmente
# le aree di molte figure
#
# Vediamo come calcolare l'integrale di una funzione definita per punti:
# Le aree sono orientate: positive/negative se stanno sopra/sotto l'asse x
# (figure sopra a destra)
f1 <- function(x) -x^2+1; f2 <- function(x) -f1(x)
BF=3; HF=3
PIANO(-1,1, -1,1); areaF(f1,-1,1,2000) # 1.333333
PIANO(-1,1, -1,1); areaF(f2,-1,1,2000) # -1.333333
# Calcolando opportuni integrali (vedi sotto) posso calcolare facilmente
# le aree di molte figure
#
# Vediamo come calcolare l'integrale di una funzione definita per punti:
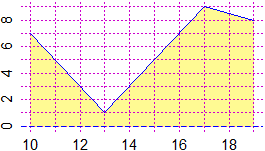 x = c(10,13, 17, 19); y = c(7,1,9,8)
Piano(min(x),max(x), 0,max(y)); spezza(x,y,"blue")
integr = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
integr(x,y) # 49
#
# lunghezza curve. Esempi (nei vari modi) per il calcolo della semicirconferenza
x = c(10,13, 17, 19); y = c(7,1,9,8)
Piano(min(x),max(x), 0,max(y)); spezza(x,y,"blue")
integr = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
integr(x,y) # 49
#
# lunghezza curve. Esempi (nei vari modi) per il calcolo della semicirconferenza
| 3.141593 | 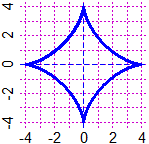 | lungh.= 24
area = 6 π
|
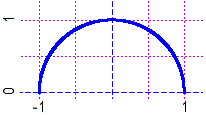 |
# descrizione come funzione (input: f, A,B, N)
f = function(x) sqrt(1-x^2)
# descrizione in forma parametrica (input: f,g, A,B, N)
x = function(t) cos(t); y = function(t) sin(t)
# descrizione in forma polare (input: r, A,B, N)
# (in questo caso particolare r non dipende da ang)
r = function(ang) 1
lungFun(f, -1,1, 100); lungFun(f, -1,1, 10000); lungFun(f, -1,1, 100000)
# 3.140761 3.141592 3.141593
lungPar(x,y, 0,pi, 100); lungPar(x,y, 0,pi, 1000); lungPar(x,y, 0,pi, 10000)
# 3.141463 3.141591 3.141593
lungPolar(r, 0,pi, 100); lungPolar(r, 0,pi, 1000); lungPolar(r, 0,pi, 10000)
# 3.141463 3.141591 3.141593
# lunghezza ed area dell'asteroide - vedi (27)
# asteroide di "raggio" 4
f = function(t) 4*cos(t)^3; g = function(t) 4*sin(t)^3
PIANO(-4,4, -4,4); param(f,g, 0,2*pi, "blue") # figura sopra a destra
lungPar(f,g,0,2*pi, 5000)
# 24
A = areaPar(f,g, 0,2*pi,5000); A
# 18.84957
A = areaPar(f,g, 0,2*pi,10000); A
# 18.84956
A/pi
# 6
# Per la lunghezza di curve tridimensionali vedi qui.
#
# derivate
G <- function(a) sin(a); derivata(G,"a")
# cos(a)
f <- function(x) 3*x^3-5*x^2+x+3
graficoF(f, -2,4, "blue")
derivata(f,"x")
# 3 * (3 * x^2) - 5 * (2 * x) + 1
# per utilizzare l'espressione prodotta da "derivata" occorre valutarla con eval:
df <- function(x) eval(derivata(f,"x")); grafico(df,-3,5, "red")
# potevo anche def. df scrivendo 3*(3*x^2)-5*(2*x)+1
derivata2(f,"x")
# 3 * (3 * (2 * x)) - 5 * 2
d2f <- function(x) eval(derivata2(f,"x")); grafico(d2f,-3,5, "violet")
derivata3(f,"x")
# 3 * (3 * 2)
d3f <- function(x) eval(derivata3(f,"x"))+x-x # metto la "x" con un trucco
grafico(d3f,-3,5, "green")
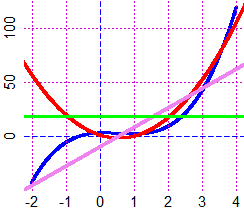 # Vedi qui per un esempio di "studio di funzione"
# Vedi qui per un esempio di "studio di funzione"
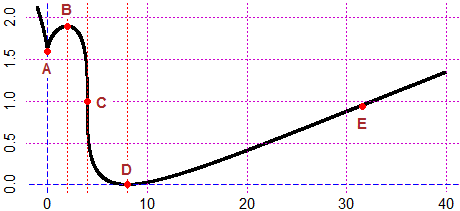 F = function(x,y,z) 5*x^2*y^3+x^3*z
derivata(F,"x"); derivata(F,"z")
# 5*(2*x)*y^3+3*x^2*z x^3
derivata2(F,"y"); derivata2(F,"z")
# 5*x^2*(3*(2*y)) 0
derivataxy(F,"x","y"); derivataxy(F,"x","z")
# 5*(2*x)*(3*y^2) 3*x^2
#
Q = function(x,y) x^4+6*x^2*y^2+y^4-32*(x^2+y^2)
# per calcolare l'hessiano le variabili devono essere x ed y
hessiano(Q,0,0), hessiano(Q,0,4); hessiano(Q,2,-2)
# 4096 16384 -8192
#
# integrali
g <- function(x) sin(x)
integrale(sin, 0,pi/2); integrale(sin, 0,pi); integrale(sin, 0,2*pi)
# 1 2 2.032977e-16 ("praticamente" 0)
Piano(-pi,2*pi, -1,1); grafic(cos, -pi,2*pi, "blue")
gintegra(cos, 0,2*pi, "red"); gintegra(cos, 0,-pi, "violet")
punto(0,0, "red")
F = function(x,y,z) 5*x^2*y^3+x^3*z
derivata(F,"x"); derivata(F,"z")
# 5*(2*x)*y^3+3*x^2*z x^3
derivata2(F,"y"); derivata2(F,"z")
# 5*x^2*(3*(2*y)) 0
derivataxy(F,"x","y"); derivataxy(F,"x","z")
# 5*(2*x)*(3*y^2) 3*x^2
#
Q = function(x,y) x^4+6*x^2*y^2+y^4-32*(x^2+y^2)
# per calcolare l'hessiano le variabili devono essere x ed y
hessiano(Q,0,0), hessiano(Q,0,4); hessiano(Q,2,-2)
# 4096 16384 -8192
#
# integrali
g <- function(x) sin(x)
integrale(sin, 0,pi/2); integrale(sin, 0,pi); integrale(sin, 0,2*pi)
# 1 2 2.032977e-16 ("praticamente" 0)
Piano(-pi,2*pi, -1,1); grafic(cos, -pi,2*pi, "blue")
gintegra(cos, 0,2*pi, "red"); gintegra(cos, 0,-pi, "violet")
punto(0,0, "red")
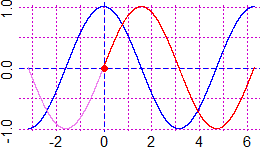 # È facile integrare numericamente e graficamente funzioni non facili da studiare "a
# mano". Vedi qui per un esempio.
# Nota 1. Se l'integrale tra -Inf e Inf viene 0 controlla se è finito anche quello tra
# 0 e Inf: se non accade significa che l'integrale diverge (è venuto 0 solo per una
# semplificazione formale)
# Nota 2. Per integrare una funzione tra a e b se essa non è definita in un punto c
# compreso tra a e b fai la somma dell'integrale tra a e c e di quello tra c e b
#
# Vedi qui come calcolare aree usando gli integrali
# È facile integrare numericamente e graficamente funzioni non facili da studiare "a
# mano". Vedi qui per un esempio.
# Nota 1. Se l'integrale tra -Inf e Inf viene 0 controlla se è finito anche quello tra
# 0 e Inf: se non accade significa che l'integrale diverge (è venuto 0 solo per una
# semplificazione formale)
# Nota 2. Per integrare una funzione tra a e b se essa non è definita in un punto c
# compreso tra a e b fai la somma dell'integrale tra a e c e di quello tra c e b
#
# Vedi qui come calcolare aree usando gli integrali
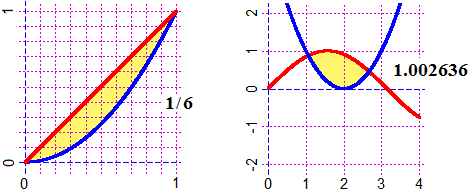 Esempi - 35 (vedi)
A <- c(1,4, 5,4, 5,0, 1,0, 1,4, 3,5, 5,4); xTab(A); yTab(A)
# 1 5 5 1 1 3 5
# 4 4 0 0 4 5 4
PIANO(0,6, 0,6); spezzata(xTab(A), yTab(A), "red")
PIANO(0,6, 0,6); spezzaC(xTab(A), yTab(A), "yellow")
Esempi - 35 (vedi)
A <- c(1,4, 5,4, 5,0, 1,0, 1,4, 3,5, 5,4); xTab(A); yTab(A)
# 1 5 5 1 1 3 5
# 4 4 0 0 4 5 4
PIANO(0,6, 0,6); spezzata(xTab(A), yTab(A), "red")
PIANO(0,6, 0,6); spezzaC(xTab(A), yTab(A), "yellow")
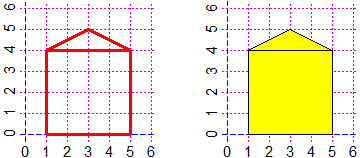 # Posso caricare coordinate (separate da ",") presenti in un file esterno.
# Ad es. se copio le coordinate presenti nel file penisola e le incollo
# dopo avere battuto
# I <- c( e infine battendo ) in modo da ottenere:
# I <- c(
# 8,46,
# 7.87,45.9,
# ...
# 8,46
# )
# Ecco che cosa ho come esito con questi altri comandi:
X <- xTab(I); Y <- yTab(I)
Piano(min(X),max(X), min(Y),max(Y)); spezzata(X,Y, "blue")
C <- centroPol(X,Y); C; PUNTI(C[1],C[2],"red")
# 12.18996 43.48932
# per centroPol vedi 25
Piano(min(X),max(X), min(Y),max(Y)); spezzaC(X,Y, "green"); spezza(X,Y, "red")
PUNTI(C[1],C[2],"red")
# Posso caricare coordinate (separate da ",") presenti in un file esterno.
# Ad es. se copio le coordinate presenti nel file penisola e le incollo
# dopo avere battuto
# I <- c( e infine battendo ) in modo da ottenere:
# I <- c(
# 8,46,
# 7.87,45.9,
# ...
# 8,46
# )
# Ecco che cosa ho come esito con questi altri comandi:
X <- xTab(I); Y <- yTab(I)
Piano(min(X),max(X), min(Y),max(Y)); spezzata(X,Y, "blue")
C <- centroPol(X,Y); C; PUNTI(C[1],C[2],"red")
# 12.18996 43.48932
# per centroPol vedi 25
Piano(min(X),max(X), min(Y),max(Y)); spezzaC(X,Y, "green"); spezza(X,Y, "red")
PUNTI(C[1],C[2],"red")
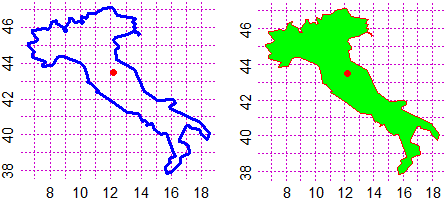 # Vedi qui per caricare dati come quelli di "penisola" salvati come tabella
#
# Un pipistrello:
boxmN(-6,6, -6,6) # con PIANO(-6,6, -6,6) avrei anche la griglia; con PIANOss(-6,6, -6,6)
# non avrei la griglia ma l'immagine riempirebbe meno la finestra
P <- c(
0, 1.05, 0.1,1.05, 0.35,1, 0.8,1.3, 0.6,0.95,
1.5,0.9, 5,4, 5.55,4, 6,3, 5,1,
1.45,-1.9, 1.8,-2.4, 1.6,-2.5, 1.35,-2, 0,-2.9,
-1.35,-2, -1.6,-2.5, -1.8,-2.4, -1.45,-1.9, -5,1,
-6,3, -5.55,4, -5,4, -1.5,0.9, -0.6,0.95,
-0.8,1.3, -0.35,1, -0.1,1.05, 0,1.05 )
X <- xTab(P); Y <- yTab(P)
spezzaC(X,Y,"grey"); spezzata(X,Y,"black")
# Vedi qui per caricare dati come quelli di "penisola" salvati come tabella
#
# Un pipistrello:
boxmN(-6,6, -6,6) # con PIANO(-6,6, -6,6) avrei anche la griglia; con PIANOss(-6,6, -6,6)
# non avrei la griglia ma l'immagine riempirebbe meno la finestra
P <- c(
0, 1.05, 0.1,1.05, 0.35,1, 0.8,1.3, 0.6,0.95,
1.5,0.9, 5,4, 5.55,4, 6,3, 5,1,
1.45,-1.9, 1.8,-2.4, 1.6,-2.5, 1.35,-2, 0,-2.9,
-1.35,-2, -1.6,-2.5, -1.8,-2.4, -1.45,-1.9, -5,1,
-6,3, -5.55,4, -5,4, -1.5,0.9, -0.6,0.95,
-0.8,1.3, -0.35,1, -0.1,1.05, 0,1.05 )
X <- xTab(P); Y <- yTab(P)
spezzaC(X,Y,"grey"); spezzata(X,Y,"black")
 Esempi - 36 (vedi)
x <- c(-0.2, 1.3, 1.7, 3.2, 4.1, 4.6)
y <- c(9.1, 17.5, 20.7, 25.4, 35.7, 51.2)
Piano(-1,6,-10,70); PUNTI(x,y,1)
regressione(x,y, 0,0); PUNTI(0,0,"blue")
# 9.829 * x
f <- function(x) 9.829 * x; grafico(f,-1,6, "red")
regressione1(x,y)
# 7.628 * x + 7.911
g <- function(x) 7.628 * x + 7.911; grafico(g,-1,6, "blue")
regressione2(x,y)
# 1.37 * x^2 + 1.38 * x + 11.2
h <- function(x) 1.37 * x^2 + 1.38 * x + 11.2; grafico(h,-1,6, "violet")
regressione3(x,y)
# 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6
k <- function(x) 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6; grafico(k,-1,6, "green")
PUNTI(0,0,"blue"); PUNTI(x,y,1)
Esempi - 36 (vedi)
x <- c(-0.2, 1.3, 1.7, 3.2, 4.1, 4.6)
y <- c(9.1, 17.5, 20.7, 25.4, 35.7, 51.2)
Piano(-1,6,-10,70); PUNTI(x,y,1)
regressione(x,y, 0,0); PUNTI(0,0,"blue")
# 9.829 * x
f <- function(x) 9.829 * x; grafico(f,-1,6, "red")
regressione1(x,y)
# 7.628 * x + 7.911
g <- function(x) 7.628 * x + 7.911; grafico(g,-1,6, "blue")
regressione2(x,y)
# 1.37 * x^2 + 1.38 * x + 11.2
h <- function(x) 1.37 * x^2 + 1.38 * x + 11.2; grafico(h,-1,6, "violet")
regressione3(x,y)
# 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6
k <- function(x) 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6; grafico(k,-1,6, "green")
PUNTI(0,0,"blue"); PUNTI(x,y,1)
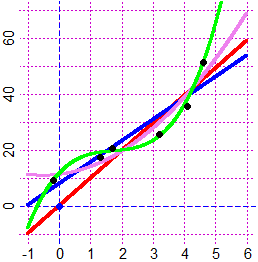
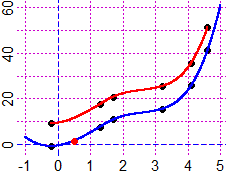 # A destra è rappresenta invece la spline cubica che interpola i punti (vedi):
Piano(-1,6,-10,70); PUNTI(x,y,1); L=spline(x,y,1000)
# ho calcolato e messo in L le coordinate di 1000 punti della
# spline passante per i punti x,y
spezzata(L$x,L$y,"red") # l'ho tracciata in rosso
# Quella "prolungata" che passa per gli stessi punti abbassati di 10
PUNTI(x,y-10,1); L1=spline(x,y-10,1000, xmin=-1,xmax=5)
spezzata(L1$x,L1$y, "blue")
#
# La curva che passa esattamente per (-1,-10),(0,-1),(1,-2),(2,5)
PIANO(-2,3,-20,20)
punto(-1,-10, 1); punto(0,-1,"red"); punto(1,-2,"green"); punto(2,5,"blue")
regressione3( c(-1,0,1,2), c(-10,-1,-2,5) )
# 3 * x^3 + -5 * x^2 + 1 * x + -1
f <- function(x) 3 * x^3 + -5 * x^2 + 1 * x + -1
grafico(f,-2,3, 6)
# A destra è rappresenta invece la spline cubica che interpola i punti (vedi):
Piano(-1,6,-10,70); PUNTI(x,y,1); L=spline(x,y,1000)
# ho calcolato e messo in L le coordinate di 1000 punti della
# spline passante per i punti x,y
spezzata(L$x,L$y,"red") # l'ho tracciata in rosso
# Quella "prolungata" che passa per gli stessi punti abbassati di 10
PUNTI(x,y-10,1); L1=spline(x,y-10,1000, xmin=-1,xmax=5)
spezzata(L1$x,L1$y, "blue")
#
# La curva che passa esattamente per (-1,-10),(0,-1),(1,-2),(2,5)
PIANO(-2,3,-20,20)
punto(-1,-10, 1); punto(0,-1,"red"); punto(1,-2,"green"); punto(2,5,"blue")
regressione3( c(-1,0,1,2), c(-10,-1,-2,5) )
# 3 * x^3 + -5 * x^2 + 1 * x + -1
f <- function(x) 3 * x^3 + -5 * x^2 + 1 * x + -1
grafico(f,-2,3, 6)
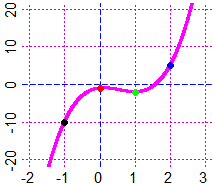 Esempi - 37 (vedi)
xx <- c(-1,-1,0,0,1,1)
yy <- c(0,1,1,-1,-1,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,0); bezier(xx,-yy,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,"red"); bezier(xx,-yy,"black")
Esempi - 37 (vedi)
xx <- c(-1,-1,0,0,1,1)
yy <- c(0,1,1,-1,-1,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,0); bezier(xx,-yy,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,"red"); bezier(xx,-yy,"black")
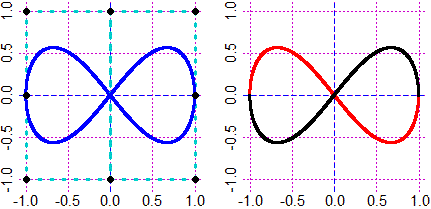 # altri esempi qui
Esempi - 38 (vedi)
x <- c(0,2,3,6); y <- c(1,2,4,5)
rigcol(2,3) # 2 righe e 3 colonne
Boxm_(0,6,0,6); Spezzata(x,y, "blue"); Boxm_(0,6,0,6); Spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzata(x,y, "blue"); Boxm_(0,6,0,6); spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzat(x,y, "blue"); Boxm_(0,6,0,6); PUNTI(x,y, "blue")
# Boxm_ apre una finestra nel riquadro monometrica, lasciando i margini
# altri esempi qui
Esempi - 38 (vedi)
x <- c(0,2,3,6); y <- c(1,2,4,5)
rigcol(2,3) # 2 righe e 3 colonne
Boxm_(0,6,0,6); Spezzata(x,y, "blue"); Boxm_(0,6,0,6); Spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzata(x,y, "blue"); Boxm_(0,6,0,6); spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzat(x,y, "blue"); Boxm_(0,6,0,6); PUNTI(x,y, "blue")
# Boxm_ apre una finestra nel riquadro monometrica, lasciando i margini
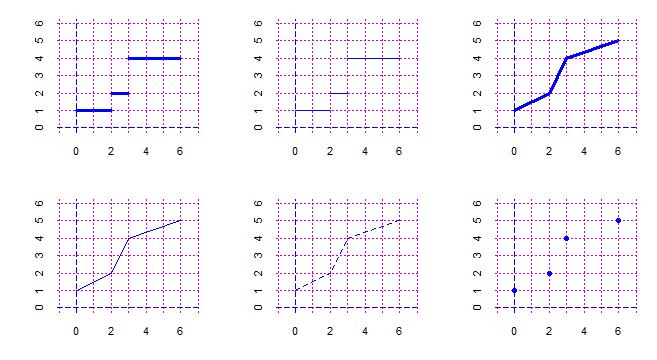 rigcol(2,3)
Box_(0,6,0,6); Spezzata(x,y, "blue"); Box_(0,6,0,6); Spezza(x,y, "blue")
Box_(0,6,0,6); spezzata(x,y, "blue"); Box_(0,6,0,6); spezza(x,y, "blue")
Box_(0,6,0,6); spezzat(x,y, "blue"); Box_(0,6,0,6); PUNTI(x,y, "blue")
# Box_ apre una finestra nel riquadro, lasciando i margini
rigcol(2,3)
Box_(0,6,0,6); Spezzata(x,y, "blue"); Box_(0,6,0,6); Spezza(x,y, "blue")
Box_(0,6,0,6); spezzata(x,y, "blue"); Box_(0,6,0,6); spezza(x,y, "blue")
Box_(0,6,0,6); spezzat(x,y, "blue"); Box_(0,6,0,6); PUNTI(x,y, "blue")
# Box_ apre una finestra nel riquadro, lasciando i margini
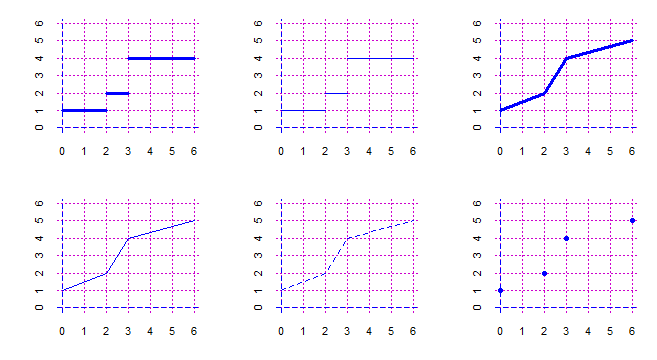 rigcol(2,3)
BoxN(0,6,0,6); BOX(); Spezzata(x,y, "blue"); BoxN(0,6,0,6); Spezza(x,y, "blue")
BoxN(0,6,0,6); spezzata(x,y, "blue"); BoxN(0,6,0,6); spezza(x,y, "blue")
BoxN(0,6,0,6); BOX(); spezzat(x,y, "blue"); BoxN(0,6,0,6); PUNTI(x,y, "blue")
# BoxN già visto in 25 (non lascia margini)
rigcol(2,3)
BoxN(0,6,0,6); BOX(); Spezzata(x,y, "blue"); BoxN(0,6,0,6); Spezza(x,y, "blue")
BoxN(0,6,0,6); spezzata(x,y, "blue"); BoxN(0,6,0,6); spezza(x,y, "blue")
BoxN(0,6,0,6); BOX(); spezzat(x,y, "blue"); BoxN(0,6,0,6); PUNTI(x,y, "blue")
# BoxN già visto in 25 (non lascia margini)
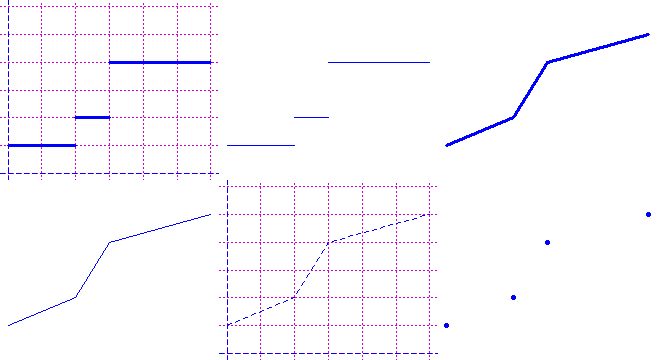 Esempi - 39 (vedi)
# Soluzione grafica di eq.diff. del 1° ord. col metodo di Eulero:
# soledif(x0,y0,xf,N,col) traccia la poligonale approssimante con N passi il graf. della
# sol. di y' = f(x,y) (quella passante per (x0,y0), da x0 a xf), con f messa in Dy
# Esempio: y'=x-y tale che (x0,y0)=(-1,3) per -1 <= x <= 5
Dy <- function(x,y) x-y
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "brown")
soledif(-1,3, 5, 1e3, "blue")
# Capisco che con N = 1000 il grafico si è stabilizzato. In genere N = 1e4
soledif(4,2.5, -1, 1e4, "red")
# è sufficiente; se il grafico ha molte oscillazioni occorre aumentare N
# Se voglio vedere il campo direzionale per 20 righe e 25 colonne faccio
diredif(-1,5, -2,5, 25,20)
# Se voglio vedere solo questo non metto le righe "soledif"
# Altri esempi per la stessa equazione (fig. a destra):
Piano(-1,5, -2,5)
soledif(1,0, 5, 1e4, "brown"); soledif(1,0, -1, 1e4, "blue")
soledif(2,1.5, 5, 1e4, "brown"); soledif(2,1.5, -1, 1e4, "blue")
soledif(3,1, 5, 1e4, "brown"); soledif(3,1, -1, 1e4, "blue")
Esempi - 39 (vedi)
# Soluzione grafica di eq.diff. del 1° ord. col metodo di Eulero:
# soledif(x0,y0,xf,N,col) traccia la poligonale approssimante con N passi il graf. della
# sol. di y' = f(x,y) (quella passante per (x0,y0), da x0 a xf), con f messa in Dy
# Esempio: y'=x-y tale che (x0,y0)=(-1,3) per -1 <= x <= 5
Dy <- function(x,y) x-y
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "brown")
soledif(-1,3, 5, 1e3, "blue")
# Capisco che con N = 1000 il grafico si è stabilizzato. In genere N = 1e4
soledif(4,2.5, -1, 1e4, "red")
# è sufficiente; se il grafico ha molte oscillazioni occorre aumentare N
# Se voglio vedere il campo direzionale per 20 righe e 25 colonne faccio
diredif(-1,5, -2,5, 25,20)
# Se voglio vedere solo questo non metto le righe "soledif"
# Altri esempi per la stessa equazione (fig. a destra):
Piano(-1,5, -2,5)
soledif(1,0, 5, 1e4, "brown"); soledif(1,0, -1, 1e4, "blue")
soledif(2,1.5, 5, 1e4, "brown"); soledif(2,1.5, -1, 1e4, "blue")
soledif(3,1, 5, 1e4, "brown"); soledif(3,1, -1, 1e4, "blue")
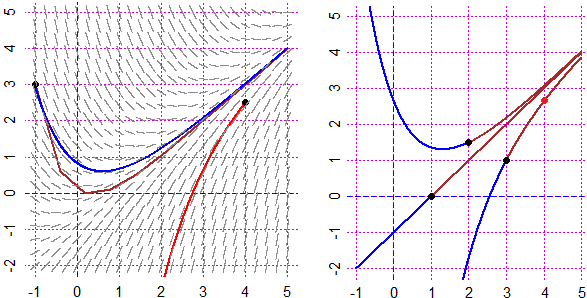 # soledifp(x0,y0,xf,N,col) traccia solo gli N+1 punti senza congiungerli
Piano(-1,5, -2,5)
soledifp(-1,3, 5, 10, "black")
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "red")
soledifp(-1,3, 5, 10, "black")
# soledifp(x0,y0,xf,N,col) traccia solo gli N+1 punti senza congiungerli
Piano(-1,5, -2,5)
soledifp(-1,3, 5, 10, "black")
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "red")
soledifp(-1,3, 5, 10, "black")
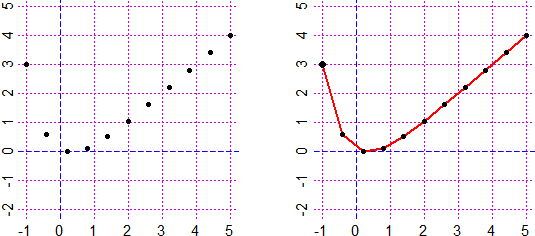 Esempi - 40 (vedi)
casa()
( poi premi INVIO per far partire il programma )
# teta, fi e ind.dist indicano la posizione dell'occhio: la direzione
# dello sguardo proiettata sul piano orizzontale, la sua inclinazione
# rispetto a tale piano e la distanza dell'occhio dal centro del box.
Esempi - 40 (vedi)
casa()
( poi premi INVIO per far partire il programma )
# teta, fi e ind.dist indicano la posizione dell'occhio: la direzione
# dello sguardo proiettata sul piano orizzontale, la sua inclinazione
# rispetto a tale piano e la distanza dell'occhio dal centro del box.
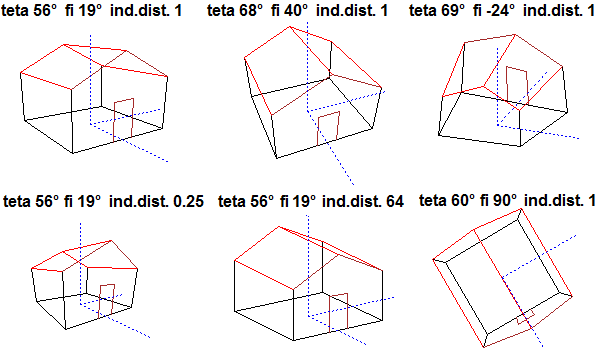 GRAF3DIM()
Se batti GRAF3D(10,5,1) vedi il grafico della funzione che dentro
al cerchio di centro (0,0) e raggio 1 vale sqrt(x^2+y^2) e al
di fuori vale 0, vista dalla direzione teta=10°, fi=5° e da una
particolare distanza. Con GRAF3D(10,5,3) allontani l'occhio.
Prova con GRAF3D(0,30,1/2) GRAF3D(10,30,2) GRAF3D(10,-30,2)
GRAF3DIM()
Se batti GRAF3D(10,5,1) vedi il grafico della funzione che dentro
al cerchio di centro (0,0) e raggio 1 vale sqrt(x^2+y^2) e al
di fuori vale 0, vista dalla direzione teta=10°, fi=5° e da una
particolare distanza. Con GRAF3D(10,5,3) allontani l'occhio.
Prova con GRAF3D(0,30,1/2) GRAF3D(10,30,2) GRAF3D(10,-30,2)
 BOH()
Se batti INCL(5,10) vedi una figura da una inclinazione di 5°, con
scala tale che le porzioni di assi x,y,z (colorati nero, verde e
rosso) siano lunghe 10. La stiamo guardando un po' a sinistra del
piano yz. La figura è una parabola. E' possibile? Prova con
INCL(10,10), INCL(15,10), INCL(40,10), INCL(40,200), INCL(40,2000)
INCL(5,10)
BOH()
Se batti INCL(5,10) vedi una figura da una inclinazione di 5°, con
scala tale che le porzioni di assi x,y,z (colorati nero, verde e
rosso) siano lunghe 10. La stiamo guardando un po' a sinistra del
piano yz. La figura è una parabola. E' possibile? Prova con
INCL(10,10), INCL(15,10), INCL(40,10), INCL(40,200), INCL(40,2000)
INCL(5,10)
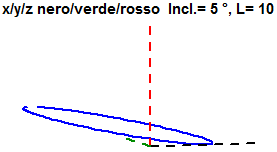
# Un'immagine simile al S.Sebastiano di Antonello da Messina
# (alto 1.80 cm visto dal pittore dall'altezza di 0.30 m)
# Prova a cambiare il punto di vista (direzione e distanza).
seba(0) seba(1)
( poi premi INVIO per far paratire il programma )
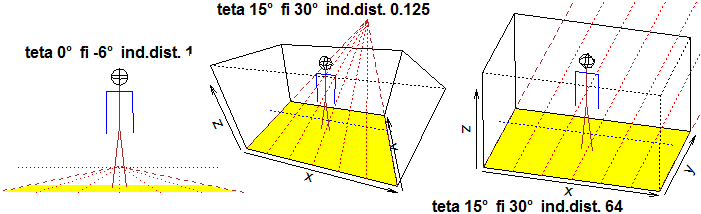 |  |
Esempi - 41 (vedi)
Con Dado(1) e DadoB(1) viene visualizzata l'uscita di un dado. Con Dado(N) e DadoB(N) con
N ≥ 2 ne vengono generate N e ne viene visualizzato l'istogramma di distribuzione.
Uno dei due dadi è realizzato in legno, l'altro col cartoncino, nel modo illustrato sotto;
batti DADO() se vuoi avere lo sviluppo del dado che puoi usare per costruirlo.
Quali sono gli istogrammi di distribuzione dei due dadi?
Fai delle prove, con N ≤ 20000, e valuta la probabilità con cui l'uscita è minore o eguale
a 3 in un caso e nell'altro.
Quale tra Dado(1) e DadoB(1) useresti per realizzare un gioco non truccato?
Dado2(N) e DadoB2(N) (con N>1) visualizzano la distribuzione di N uscite del lancio
di 2 dadi.
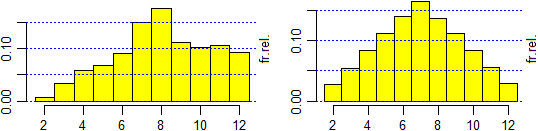 Esempi - 42 (vedi)
# Batti ripetutamente escher() Otterrai successive tassellazioni casuali.
escher();
escher();
...
Vedi qui per approfondimenti.
Esempi - 42 (vedi)
# Batti ripetutamente escher() Otterrai successive tassellazioni casuali.
escher();
escher();
...
Vedi qui per approfondimenti.
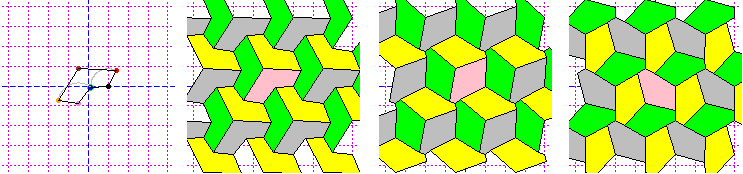 Esempi - 43 (vedi)
struttura(1*2+3) # la somma (+) del prodotto (*) di 1 per 2 e di 3
# `+`
# `*`
# [1] 1
# [1] 2
# [1] 3
struttura(1+2*3) # la "+" di 1 e del "*" di 2 per 3
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
struttura(1+2*3+4) # la "+" della ("+" di 1 e del "*" di 2 per 3) e di 4
# `+`
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
# [1] 4
struttura( 1*(2+3) ) # il "*" di 1 per la "+" di 2 e 3
# `*`
# [1] 1
# `(`
# `+`
# [1] 2
# [1] 3
# La parentesi "(" compare solo per specificare che il 2º termine di * non è un singolo
# termine [questo è il motivo per cui non compare ")"]
struttura( -sqrt(1+2)*3 ) # il "*" della "negaz" della ("√" della "+" di 1 e 2) per 3
# `*`
# `-`
# sqrt
# `+`
# [1] 1
# [1] 2
# [1] 3
struttura( -1-2*3^-4 ) # la "-" tra la "negaz" di 1 e il "*" di 2 per (3 alla "negaz" di 4)
# `-`
# `-`
# [1] 1
# `*`
# [1] 2
# `^`
# [1] 3
# `-`
# [1] 4
Esempi - 44 (vedi)
Per la realizzazione di grafi ad albero con opportuni comandi vedi qui.
Per realizzare grafi di flusso vedi qui.
Esempi - 43 (vedi)
struttura(1*2+3) # la somma (+) del prodotto (*) di 1 per 2 e di 3
# `+`
# `*`
# [1] 1
# [1] 2
# [1] 3
struttura(1+2*3) # la "+" di 1 e del "*" di 2 per 3
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
struttura(1+2*3+4) # la "+" della ("+" di 1 e del "*" di 2 per 3) e di 4
# `+`
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
# [1] 4
struttura( 1*(2+3) ) # il "*" di 1 per la "+" di 2 e 3
# `*`
# [1] 1
# `(`
# `+`
# [1] 2
# [1] 3
# La parentesi "(" compare solo per specificare che il 2º termine di * non è un singolo
# termine [questo è il motivo per cui non compare ")"]
struttura( -sqrt(1+2)*3 ) # il "*" della "negaz" della ("√" della "+" di 1 e 2) per 3
# `*`
# `-`
# sqrt
# `+`
# [1] 1
# [1] 2
# [1] 3
struttura( -1-2*3^-4 ) # la "-" tra la "negaz" di 1 e il "*" di 2 per (3 alla "negaz" di 4)
# `-`
# `-`
# [1] 1
# `*`
# [1] 2
# `^`
# [1] 3
# `-`
# [1] 4
Esempi - 44 (vedi)
Per la realizzazione di grafi ad albero con opportuni comandi vedi qui.
Per realizzare grafi di flusso vedi qui.

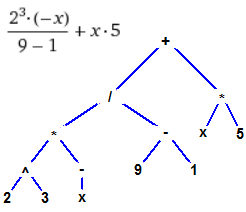
 Esempi - 45 (vedi)
Vai qui
Esempi - 45 (vedi)
Vai qui


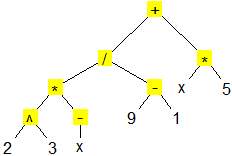 # Controlliamo la struttura dell'ultimo grafo:
struttura( (1^2)*-3/(4-5)+6*7 )
# `+`
# `/`
# `*`
# `(`
# `^`
# [1] 1
# [1] 2
# `-`
# [1] 3
# `(`
# `-`
# [1] 4
# [1] 5
# `*`
# [1] 6
# [1] 7
# Un esercizio:
# dalle uscite relative a un termine incognito risalire ad esso e al grafo.
`+`
`/`
`*`
A
`-`
`(`
`+`
A
B
`(`
`-`
A
`(`
`+`
C
D
E
# Controlliamo la struttura dell'ultimo grafo:
struttura( (1^2)*-3/(4-5)+6*7 )
# `+`
# `/`
# `*`
# `(`
# `^`
# [1] 1
# [1] 2
# `-`
# [1] 3
# `(`
# `-`
# [1] 4
# [1] 5
# `*`
# [1] 6
# [1] 7
# Un esercizio:
# dalle uscite relative a un termine incognito risalire ad esso e al grafo.
`+`
`/`
`*`
A
`-`
`(`
`+`
A
B
`(`
`-`
A
`(`
`+`
C
D
E
+
_______________/ \_______________
/ E
_______/ \_______
* -
__/ \__ __/ \__
A - A +
| / \
+ C D
/ \
A B
+
_______________/ \_______________
/ E
_______/ \_______
* -
__/ \__ __/ \__
A - A +
| / \
+ C D
/ \
A B
+
_______________/ \_______________
/ E
_______/ \_______
* -
__/ \__ __/ \__
A - A +
| / \
+ C D
/ \
A B
+
_______________/ \_______________
/ E
_______/ \_______
* -
__/ \__ __/ \__
A - A +
| / \
+ C D
/ \
A B
+
_______________/ \_______________
/ E
_______/ \_______
* -
__/ \__ __/ \__
A - A +
| / \
+ C D
/ \
A B
# Quindi: A*-(A+B)/(A-(C+D)) + E
# Verifica:
struttura( A*-(A+B)/(A-(C+D)) + E )
...
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
#
# Da "Esempi - 35".
# Il file penisola utilizzato sopra lo abbiamo copiato e poi incollato in R. Vediamo
# come si sarebbe potuto procedere se avessimo caricato direttamente i dati da un
# file di testo con questo contenuto:
# penisola italiana
8,46
7.87,45.9
7.6,45.95
...
8,46
# Vediamo come si può esaminare il contenuto di un file. Con
readLines("http://macosa.dima.unige.it/R/penisola.txt",n=4)
# comando la visualizzazione delle prime 4 righe del file "penisola.txt". Ottengo:
# "# penisola italiana" "8,46" "7.87,45.9" "7.6,45.95"
# Capisco che il file è una tabella di coppie di dati preceduta da un commento;
# solo il primo e il secondo elemento di ogni coppia sono separati da ",".
# Metto la tabella in un file (chiamiamolo "T") col seguente comando, in cui
# specifico che devo saltare (skip) una riga (il commento) e che i dati
# sono separati da ",":
T <- read.table("http://macosa.dima.unige.it//R/penisola.txt",skip=1,sep=",")
# Non stampo la tabella per non occupare spazio; la visualizzo con:
data.entry(T) # Compare la finestra seguente che poi chiudo:
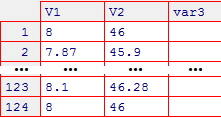 # Le due colonne di dati sono chiamate V1 e V2. Le metto in X e Y con:
X <- T$V1; Y <- T$V2 # Volendo guardo i dati con data.entry(X) e ...(Y)
# Procedo come sopra:
HF=4; BF=4
Piano(min(X),max(X), min(Y),max(Y)); spezza(X,Y, "blue")
C <- centroPol(X,Y); PUNTO(C[1],C[2], "black")
# Le due colonne di dati sono chiamate V1 e V2. Le metto in X e Y con:
X <- T$V1; Y <- T$V2 # Volendo guardo i dati con data.entry(X) e ...(Y)
# Procedo come sopra:
HF=4; BF=4
Piano(min(X),max(X), min(Y),max(Y)); spezza(X,Y, "blue")
C <- centroPol(X,Y); PUNTO(C[1],C[2], "black")
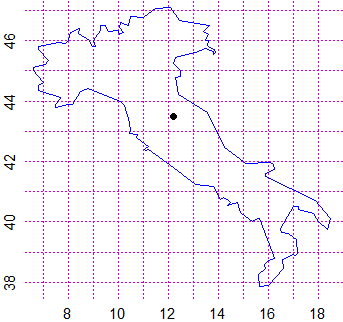 #
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice
# (da 01 a 23 i comandi scritti in blu sono illustrati nel documento precedente):
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
abs sign rad2-rad5 factorial choose %/% ?Math gradi funz.circolari
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
prod
# 06 Rivedere i comandi (^ v). function
cancellare variabili messaggi d'errore str
# 07 Arrotondare numeri e risultati.
trunc print signif piu ultimo write cat tabulazioni
# 08 Le sequenze di numeri: seq :
ricorsione
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
operare su varie finestre grafiche
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
arco P()
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
l'indicazione dei colori con numeri
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
semir r2p a2p cartamm rect
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
poligono regolare poligo poligoC
spezzaL spezza2L text \n frec2 freccia2 Direzionex Direzioney
RotTraMol MolTraRot xpunta ypunta (il punto finale dell'ultimo segmento)
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
scriviC scriviR scriviRC
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
sottoassex suAssex sottoassex ...
# 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm1/…, TERMOMETRO
tortaC TortaC TortaM StrisciaC Torta2C … torta2 torta_C …
BarreC BARREC BARRE BARRE2
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
quantile(daticlas, …) boxAB hist
Approfondimenti (simulazioni)
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
curva cur graficF grafic grafiF grafi distPF (distanza punto-grafico)
# 23 Risolvere equazioni (soluz).
soluz2 equazioni polinomiali solpol sommap prodp
if for while { } connettivi
####
# 24 Calcolo approssimato.
# approssima approssima2 EPS
# 25 Animazioni e altro su Finestre e Punti. Centroide (baricentro)
# boxN BoxN boxmN BoxmN BOX() BOXs() BOXg() NF() PPP() puntiB puntiniB punticiniB
# palliniB puntiBm puntiniBm punticiniBm palliniBm Spezzata Spezza spezzat
# puntoO puntoV puntoD puntiO/V/D linea Linea LInea centroPol
# 26 Orologi e pause
# Ore Minuti Secondi Sec attendi orologio orologio2
# 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
# param polar para par1 pola pol1 rottramol rottra moltrarot ZZZ
# 28 Calcoli tra interi comunque grandi. Stringhe <-> Numeri Basi ≠ dieci
# som pro dif app strtoi nchar substr NUMERO paste0 as.roman MNB
# 29 Disequazioni
# diseq diseq1 diseq2
# 30 Curve al variare dei parametri
# fun3p polar3p curva4p
# 31 Punti dotati di precisione. Retta approssimante
# puntiapp
# 32 Risoluzione di sistemi lineari e di sistemi in due incognite
# sistema soluzione
# 33 Pendenza di un grafico
# pend
# 34 Calcolo vettor., differenz. e integrale, lunghezze ed aree
# (e num. complessi, matrici, funz. più var., limiti, serie)
# prodv prods modulo versore derivata integrale gintegrale gintegra
# lungFun lungPar lungPolar areaPar areaPolar derivataxy hessiano
# 35 Immagini date le coordinate
# xTab yTab
# 36 Regressione, spline
# regressione regressione1 regressione2 regressione3 spline
# 37 Curve di Bezier
# 38 Grafici multipli
# rigcol colrig
# 39 Equazioni differenziali
# soledif diredif
# 40 Prospettiva
# 41 Lancio di dadi
# 42 Escher
# 43 Struttura dei termini
# 44 Grafi ad albero
# 45 Altre immagini
#
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice
# (da 01 a 23 i comandi scritti in blu sono illustrati nel documento precedente):
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
abs sign rad2-rad5 factorial choose %/% ?Math gradi funz.circolari
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
prod
# 06 Rivedere i comandi (^ v). function
cancellare variabili messaggi d'errore str
# 07 Arrotondare numeri e risultati.
trunc print signif piu ultimo write cat tabulazioni
# 08 Le sequenze di numeri: seq :
ricorsione
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
operare su varie finestre grafiche
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
arco P()
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
l'indicazione dei colori con numeri
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
semir r2p a2p cartamm rect
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
poligono regolare poligo poligoC
spezzaL spezza2L text \n frec2 freccia2 Direzionex Direzioney
RotTraMol MolTraRot xpunta ypunta (il punto finale dell'ultimo segmento)
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
scriviC scriviR scriviRC
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
sottoassex suAssex sottoassex ...
# 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm1/…, TERMOMETRO
tortaC TortaC TortaM StrisciaC Torta2C … torta2 torta_C …
BarreC BARREC BARRE BARRE2
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
quantile(daticlas, …) boxAB hist
Approfondimenti (simulazioni)
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
curva cur graficF grafic grafiF grafi distPF (distanza punto-grafico)
# 23 Risolvere equazioni (soluz).
soluz2 equazioni polinomiali solpol sommap prodp
if for while { } connettivi
####
# 24 Calcolo approssimato.
# approssima approssima2 EPS
# 25 Animazioni e altro su Finestre e Punti. Centroide (baricentro)
# boxN BoxN boxmN BoxmN BOX() BOXs() BOXg() NF() PPP() puntiB puntiniB punticiniB
# palliniB puntiBm puntiniBm punticiniBm palliniBm Spezzata Spezza spezzat
# puntoO puntoV puntoD puntiO/V/D linea Linea LInea centroPol
# 26 Orologi e pause
# Ore Minuti Secondi Sec attendi orologio orologio2
# 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
# param polar para par1 pola pol1 rottramol rottra moltrarot ZZZ
# 28 Calcoli tra interi comunque grandi. Stringhe <-> Numeri Basi ≠ dieci
# som pro dif app strtoi nchar substr NUMERO paste0 as.roman MNB
# 29 Disequazioni
# diseq diseq1 diseq2
# 30 Curve al variare dei parametri
# fun3p polar3p curva4p
# 31 Punti dotati di precisione. Retta approssimante
# puntiapp
# 32 Risoluzione di sistemi lineari e di sistemi in due incognite
# sistema soluzione
# 33 Pendenza di un grafico
# pend
# 34 Calcolo vettor., differenz. e integrale, lunghezze ed aree
# (e num. complessi, matrici, funz. più var., limiti, serie)
# prodv prods modulo versore derivata integrale gintegrale gintegra
# lungFun lungPar lungPolar areaPar areaPolar derivataxy hessiano
# 35 Immagini date le coordinate
# xTab yTab
# 36 Regressione, spline
# regressione regressione1 regressione2 regressione3 spline
# 37 Curve di Bezier
# 38 Grafici multipli
# rigcol colrig
# 39 Equazioni differenziali
# soledif diredif
# 40 Prospettiva
# 41 Lancio di dadi
# 42 Escher
# 43 Struttura dei termini
# 44 Grafi ad albero
# 45 Altre immagini
Comando (Paragrafo "qui") (Paragrafo in "Es. d'uso di base")
|
| 03 | |
: | 08 |
|
?Math %/% %% (funzioni) | 03 |
| [^] [v] | 06 |
[…] # | 01 |
[…] | 05 |
| [X] | 12 |
{ } | 23 |
= -> <- | 04 |
| abline | 20 |
abs | 03 |
Albero | 03 |
| altrestat | 20 |
analisiTesto | 20 |
angolo cerchioA cerchio3pA | 17 |
| app | 28 |
approssima … EPS | 24 |
arc arco | 13 |
| areaPol | 16 |
areaF areaPar areaPolar | 34 |
as.roman | 28 |
| 15 |
attendi | 26 |
ATTESA | 21 |
| Barre cartamm1 QUADRETTI | 19 |
BarreC BARRE BARRE2 … | 19 |
bezier | 37 |
| BF HF | 11 |
BOH | 40 |
boxAB | 20 |
| boxN BoxN boxmN … BOX … | 25 |
break | 23 |
c(…) | 05 |
| CANCELLA | 25 |
casa | 40 |
cartamm cMmM cErChi | 15 |
| cat | 07 |
centroPol (baric.) incentro | 25 |
cerchio cerchio3p centro3p | 13 |
| cerchio_cerchio | 16 |
cerch cerch3p | 13 |
cex.axis | 20 |
| choose (coeff. binomiale) | 03 |
Codifica Decodifica | 20 |
| 14 |
| coltrat | 22 |
(connettivi) | 23 |
cur curva (coniche) | 22 |
| curva4p | 30 |
Dado Dado2 | 41 |
data.entry | 35 |
| derivata … derivata6 derivataxy | 34 |
dev.new | 20 |
dev.new dev.off | 25 |
| dif | 28 |
diredif | 39 |
Direzione … dirFreccia | 16 |
| Direzione | 16 |
diseq diseq1 diseq2 | 29 |
distPF | 22 |
| distribuzione | 19 |
div divisori frazio | 09 |
e | 03 |
| escher | 42 |
factorial | 03 |
floor | 07 |
| for | 23 |
| freccia frec | freccia2 … 16 |
| 16 |
fun3p | 30 |
| function | 06 |
(funz. di più variab.) | 34 |
(gaussiana …) | 20 |
| gintegrale … | 34 |
gonio() | 19 |
gradi | 03 |
| GRAF3D | 40 |
(grafi ad albero e di flusso) | 44 |
| grafico graficoF | grafi … 22 |
| 22 |
| GRIGLIA Griglia … Griglias | 15 |
grigliaO … GrigliaV (→BOX) | 15 |
help | 23 |
| hessiano | 34 |
hist | 20 |
if ifelse | 23 |
| INPUT | 21 |
integrale | 34 |
istoclas | 20 |
| istogramma Istogramma | 20 |
length | 20 |
(limiti) | 34 |
| linea | 15 |
Linea LInea | 25 |
lung | 16 |
| lungFun lungPar lungPolar … | 34 |
(matrici) | 34 |
max min | 20 |
| max | 18 |
maxmin minmax | 22 |
MCD MCM | 09 |
| mean median | 20 |
medio2p | 15 |
Minuti | 26 |
| MNB | 28 |
modulo | 34 |
MolTraRot | 16 |
| moltrarot moltraro … | 27 |
nchar | 28 |
noClassi | 20 |
| NF | 25 |
noGriglia | 19 |
NpuntiF NPuntiF NPUNTIF | 22 |
| (numeri complessi) | 34 |
NUMERO | 28 |
Ore orologio … | 26 |
| OUTPUT | 21 |
P | 13 |
PPP (x,y punto cliccato) | 25 |
| param paramb par1 … | 27 |
pend | 33 |
pendenza inclinazione | 16 |
| PERCENTUALI pi | 21 |
| 14 |
PIANO2 Piano2 TACCHE… | 22 |
| PIANOP PianoP | 18 |
PIANOS PianoS ... Pianoss | 15 |
piu | 07 |
| polar polarb pol1 … | 27 |
polar3p | 30 |
poligono poligo poligoC | 16 |
| (polinomi) | 23 |
primi | 09 |
pro | 28 |
| prod | 05 |
prodp | 23 |
prodv prods | 34 |
| punto punti PUNTI Punti Punt | 13 |
punticino | 16 |
puntiB puntiniB palliniB … | 25 |
| puntoO puntoV puntoD … | 25 |
puntiapp | 31 |
punto_punto …_retta …_inclina | 16 |
| percentile quantile | 20 |
rad2 rad3 … | 03 |
raggio3p | 13 |
| RAPP | 10 |
RAPPORTI | 21 |
readLines read.table | 35 |
| 25 |
rect | 15 |
regressione … | 36 |
| rep | 20 |
retta_retta retta_retta2 | 16 |
| 15 |
| (ricorsione) | 08 |
rigcol colrig | 38 |
rigth=FALSE | 20 |
| rm(list=ls()) | 06 |
RotTraMol | 16 |
rottramol rottra … | 27 |
| round | 07 |
rm(list=ls()) | 06 |
runif sample set.seed | 20 |
| scrivi | (scriviC scriviR) 17 |
| 17 |
seba | 40 |
Sec Secondi | 26 |
| segm Segm semiretta | 15 |
semir | 15 |
seq | 08 |
| (serie) | 34 |
sign | 03 |
signif | 07 |
| (simulazioni, runif …) | 20 |
sistema soluzione | 32 |
soledif | 39 |
| soluz | 23 |
soluz2 solpol soluzione sommap | 23 |
som | 28 |
| sort | 09 |
sottoassex suAssex … | 18 |
spezzata spezza spezzaC | 16 |
| spezzaL spezza2L | 16 |
Spezzata Spezza spezzat … | 25 |
spline | 36 |
| sqrt | 03 |
(statistica - 1) | 20 |
stem | 20 |
| (statistica - 2) | 20 |
str (struttura dati, comandi) | 06 |
Striscia | 19 |
| StrisciaC | 19 |
strtoi | 28 |
struttura | 43 |
| suassex suassey | 18 |
suAssex SottoAssey … | 18 |
som | 28 |
| substr | 05 |
text \n (simboli) | 16 |
TERMOMETRO … torta … | 19 |
| tortaC torta2 torta_ … | 19 |
toString | 28 |
| 27 |
| trasla | 27 |
(tratteggi) | 22 |
triLLL triLAL triALA (triangoli) | 17 |
| trunc | 07 |
ultimo | 07 |
(Var Sq SqM) | 20 |
| versore | 34 |
while | 23 |
write | 07 |
| xTab yTab | 35 |
xpunta ypunta | 16 |
xrot yrot | 17 |
| xy (coord. punti cliccati) | 14 |
ZZZ | 27 |
|
 # 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# Si può rilavorare su un'immagine in un secondo tempo. Costruito un grafico o una
# figura in una finestra grafica, se batto Nome <- recordPlot() (Nome è un nome
# qualunque) l'immagine viene memorizzata. Se poi, dopo altre attività, apro una
# finestra e aziono replayPlot(Nome) viene visualizzata l'immagine iniziale, su cui
# posso continuare a lavorare. È utile anche per le animazioni (vedi 25).
# 13 punto punti Punti cerchio cerchio3p centro3p raggio3p
# Col comando arco(xCentro,yCentro, raggio, da,a, col) traccio archi di cerchio:
HF=2.5; BF=2.5; PIANO(-4,4, -4,4); cerchio(0,0, 4, "violet")
arco(-3,0, 1, 0,180, "blue"); arco(1,0, 3, 180,360, "red")
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
# Si può rilavorare su un'immagine in un secondo tempo. Costruito un grafico o una
# figura in una finestra grafica, se batto Nome <- recordPlot() (Nome è un nome
# qualunque) l'immagine viene memorizzata. Se poi, dopo altre attività, apro una
# finestra e aziono replayPlot(Nome) viene visualizzata l'immagine iniziale, su cui
# posso continuare a lavorare. È utile anche per le animazioni (vedi 25).
# 13 punto punti Punti cerchio cerchio3p centro3p raggio3p
# Col comando arco(xCentro,yCentro, raggio, da,a, col) traccio archi di cerchio:
HF=2.5; BF=2.5; PIANO(-4,4, -4,4); cerchio(0,0, 4, "violet")
arco(-3,0, 1, 0,180, "blue"); arco(1,0, 3, 180,360, "red")

 # Un altro esempio: traccio un triangolo rettangolo ed evidenzio l'angolo retto.
PIANO(-1,10, -1,10)
segm(9,1, 3,8, "red"); inclinazione(9,1, 3,8)
# [1] -49.39871 (l'inclinazione del segmento rosso)
# Traccio da 3,8 nella direzione diminuita di 90° un segmento lungo 5
Direzione(3,8, inclinazione(9,1, 3,8)-90, 5, "blue")
# Traccio da x,y del punto di arrivo di Direzione il segm. fino a 9,1
segm(Direzionex,Direzioney, 9,1, "violet")
# Traccio l'arco centrato in 3,8 di raggio 2 che va da un lato all'altro
arco(3,8, 2, inclinazione(9,1, 3,8)-90, inclinazione(9,1, 3,8), "orange")
scrivi(3,5,"90°")
#
# cerch, cerch3p, arc fanno le stesse curve di cerchio, cerchio3p, arco ma sottili.
#
# P() consente di cliccare un punto e di leggerne le coordinate. La cosa è utile in
# tutti i casi in cui si ha che fare con grafici e immagini. Può essere utile anche
# per tracciare figure, un esempio:
HF=3; BF=3; PIANO(0,10, 0,10)
P() # clicco più o meno nel punto 5,9 e ottengo;
# xP <- ... ; yP <- ...
# poi riproduco ciascuna delle righe seguenti e clicco più o meno in 2,2 8,2 5,9
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "red")
# xP <- ... ; yP <- ... cose analoghe dopo le due righe seguenti
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
# Ottengo il triangolo rosso sotto a sinistra.
# Un altro esempio: traccio un triangolo rettangolo ed evidenzio l'angolo retto.
PIANO(-1,10, -1,10)
segm(9,1, 3,8, "red"); inclinazione(9,1, 3,8)
# [1] -49.39871 (l'inclinazione del segmento rosso)
# Traccio da 3,8 nella direzione diminuita di 90° un segmento lungo 5
Direzione(3,8, inclinazione(9,1, 3,8)-90, 5, "blue")
# Traccio da x,y del punto di arrivo di Direzione il segm. fino a 9,1
segm(Direzionex,Direzioney, 9,1, "violet")
# Traccio l'arco centrato in 3,8 di raggio 2 che va da un lato all'altro
arco(3,8, 2, inclinazione(9,1, 3,8)-90, inclinazione(9,1, 3,8), "orange")
scrivi(3,5,"90°")
#
# cerch, cerch3p, arc fanno le stesse curve di cerchio, cerchio3p, arco ma sottili.
#
# P() consente di cliccare un punto e di leggerne le coordinate. La cosa è utile in
# tutti i casi in cui si ha che fare con grafici e immagini. Può essere utile anche
# per tracciare figure, un esempio:
HF=3; BF=3; PIANO(0,10, 0,10)
P() # clicco più o meno nel punto 5,9 e ottengo;
# xP <- ... ; yP <- ...
# poi riproduco ciascuna delle righe seguenti e clicco più o meno in 2,2 8,2 5,9
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "red")
# xP <- ... ; yP <- ... cose analoghe dopo le due righe seguenti
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
x <- xP; y <- yP; P(); segm((xP,yP, x,y, "red")
# Ottengo il triangolo rosso sotto a sinistra.
 # In modo analogo traccio la figura blu:
P()
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
# Poi, se voglio riprodurre la figura senza scala posso usare i valori x,y via via
# stampati, ottenendo la figura a destra (se usassi "spezzata" avrei le linee spesse)
PIANOss(0,10, 0,10)
x <- c(2,8,5,2); y <- c(2,2,9,2); spezza(x,y, "red")
x <- c(6,5,4); y <- c(2,5,2); spezza(x,y, "blue")
# 14 xy(n): le coordinate del punto che clicco. I colori.
# Puoi usare, oltre a 1 (nero), i successivi numeri interi per indicare alcuni colori (8):
HF=1; BF=4; PIANO(0,21,-1,1); for (c in 1:20) PUNTO(c,0, c)
# La cosa può essere comoda in alcuni casi
# In modo analogo traccio la figura blu:
P()
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
x <- xP; y <- yP; P(); segm(xP,yP, x,y, "blue")
# Poi, se voglio riprodurre la figura senza scala posso usare i valori x,y via via
# stampati, ottenendo la figura a destra (se usassi "spezzata" avrei le linee spesse)
PIANOss(0,10, 0,10)
x <- c(2,8,5,2); y <- c(2,2,9,2); spezza(x,y, "red")
x <- c(6,5,4); y <- c(2,5,2); spezza(x,y, "blue")
# 14 xy(n): le coordinate del punto che clicco. I colori.
# Puoi usare, oltre a 1 (nero), i successivi numeri interi per indicare alcuni colori (8):
HF=1; BF=4; PIANO(0,21,-1,1); for (c in 1:20) PUNTO(c,0, c)
# La cosa può essere comoda in alcuni casi
 # Col comando Ncolori() posso richiamare i numeri associati ai colori:
Ncolori()
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet, 7 yellow, 8 grey
# Più in generale puoi specificare i colori indicandoli con rgb(a,b,c) con a,b,c numeri
# tra 0 ed 1 che indicano la quantità di rosso (red), verde (green) e blu (blue) che li
# formano: PUNTO(2,3, rgb(1,0,0) ) fa il punto (2,3) rosso, PUNTO(4,5, rgb(1,0.5,0) )
# fa (4,5) arancione, PUNTO(3,2, rgb(0.7,0.7,0.7) ) fa (3,2) grigio
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# Per altri modi di realizzare un piano senza griglie vedi il punto 25
# semir, r2p e a2p funzionano come semiretta, retta2p e asse2p ma usano tratti sottili.
# cartamm consente di realizzare carta millimetrata. Volendo posso tracciarvi grafici o
# (usando rect, con le coordinate di vertici opposti - in col metto il colore interno,
# in border potrei mettere quello del bordo) istogrammi:
cartamm(40,25); x <- c(1,23,38); y <- c(23,9,17); spezzata(x,y,"red")
cartamm(40,25)
rect(5,0, 10,17, col="red"); rect(10,0, 15,22, col="green")
rect(15,0, 20,9, col="blue"); rect(20,0, 25,15, col="cyan")
rect(25,0, 30,19,col="violet"); rect(30,0, 35,12, col="yellow")
# Col comando Ncolori() posso richiamare i numeri associati ai colori:
Ncolori()
#1 black, 2 red, 3 green, 4 blue, 5 cyan, 6 violet, 7 yellow, 8 grey
# Più in generale puoi specificare i colori indicandoli con rgb(a,b,c) con a,b,c numeri
# tra 0 ed 1 che indicano la quantità di rosso (red), verde (green) e blu (blue) che li
# formano: PUNTO(2,3, rgb(1,0,0) ) fa il punto (2,3) rosso, PUNTO(4,5, rgb(1,0.5,0) )
# fa (4,5) arancione, PUNTO(3,2, rgb(0.7,0.7,0.7) ) fa (3,2) grigio
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
# Per altri modi di realizzare un piano senza griglie vedi il punto 25
# semir, r2p e a2p funzionano come semiretta, retta2p e asse2p ma usano tratti sottili.
# cartamm consente di realizzare carta millimetrata. Volendo posso tracciarvi grafici o
# (usando rect, con le coordinate di vertici opposti - in col metto il colore interno,
# in border potrei mettere quello del bordo) istogrammi:
cartamm(40,25); x <- c(1,23,38); y <- c(23,9,17); spezzata(x,y,"red")
cartamm(40,25)
rect(5,0, 10,17, col="red"); rect(10,0, 15,22, col="green")
rect(15,0, 20,9, col="blue"); rect(20,0, 25,15, col="cyan")
rect(25,0, 30,19,col="violet"); rect(30,0, 35,12, col="yellow")
 # Cartamm ritraccia la carta mm sullo stesso schermo. La figura sopra a destra è stata
# ottenuta con Cartamm(40,25) (e ritracciando i rettangoli senza col=...).
# Se nel comando cartamm dò come input (50,50) l'immagine viene prodotta in dimensioni
# fissate, circa 50 mm × 50 mm. Posso rappresentare nella stessa scala cerchi come
# quelli sottostanti. Per dettagli vedi qui (le immagini seguenti sono ridotte).
# (vedi anche cartamm1(),...,cartamm3() discussi al punto 19 del documento precedente)
# Cartamm ritraccia la carta mm sullo stesso schermo. La figura sopra a destra è stata
# ottenuta con Cartamm(40,25) (e ritracciando i rettangoli senza col=...).
# Se nel comando cartamm dò come input (50,50) l'immagine viene prodotta in dimensioni
# fissate, circa 50 mm × 50 mm. Posso rappresentare nella stessa scala cerchi come
# quelli sottostanti. Per dettagli vedi qui (le immagini seguenti sono ridotte).
# (vedi anche cartamm1(),...,cartamm3() discussi al punto 19 del documento precedente)
 # 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
# Direzione punto_punto punto_retta retta_retta punto_incl poligono
# spezzaL, spezza2L operano come spezzaC evidenziando il poligono con
# linee (± fitte) con inclinazione data in input invece che con un colore
PIANO(-1,5, -1,5)
x <- c(-1,1,5,2); y <- c(0,-1,2,4); spezzaL(x,y, 45, "red")
x1 <- c(0,3,5); y1 <- c(5,-1,1); spezza2L(x1,y1, -45, "brown")
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
# Direzione punto_punto punto_retta retta_retta punto_incl poligono
# spezzaL, spezza2L operano come spezzaC evidenziando il poligono con
# linee (± fitte) con inclinazione data in input invece che con un colore
PIANO(-1,5, -1,5)
x <- c(-1,1,5,2); y <- c(0,-1,2,4); spezzaL(x,y, 45, "red")
x1 <- c(0,3,5); y1 <- c(5,-1,1); spezza2L(x1,y1, -45, "brown")


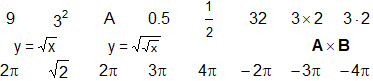 #
# Se nel comando già visto Direzione(x,y, d,r, colore) si sceglie 0 come colore il
# "raggio" lungo r da x,y nella direzione d non viene tracciato. Ciò consente di avere
# comunque in Direzionex e Direzioney le coordinate del punto di arrivo. Un esempio:
# (vedi qui per i comandi)
#
# Se nel comando già visto Direzione(x,y, d,r, colore) si sceglie 0 come colore il
# "raggio" lungo r da x,y nella direzione d non viene tracciato. Ciò consente di avere
# comunque in Direzionex e Direzioney le coordinate del punto di arrivo. Un esempio:
# (vedi qui per i comandi)
 # Altri comandi utili per tracciare figure.
# Per traslare, ruotare, moltiplicare le coordinate dei punti posso usare i comandi:
# MolTraRot(x,y, mx,my, tx,ty, ang) e RotTraMol(x,y, ang, tx,ty, mx,my). Dato (x,y) il
# primo ne moltiplica le coordinate per mx ed my, poi lo trasla di tx,ty e infine lo
# ruota attorno a (0,0) di ang. Il secondo invece prima lo ruota attorno a (0,0), poi
# lo trasla e infine ne moltiplica le coordinate. Se aggiungo al comando [1] o [2] ho
# la 1ª o la 2ª coordinata. Per operare su curve vedi 27.
# Vedi qui per un esempio, che genera la figura seguente.
# Altri comandi utili per tracciare figure.
# Per traslare, ruotare, moltiplicare le coordinate dei punti posso usare i comandi:
# MolTraRot(x,y, mx,my, tx,ty, ang) e RotTraMol(x,y, ang, tx,ty, mx,my). Dato (x,y) il
# primo ne moltiplica le coordinate per mx ed my, poi lo trasla di tx,ty e infine lo
# ruota attorno a (0,0) di ang. Il secondo invece prima lo ruota attorno a (0,0), poi
# lo trasla e infine ne moltiplica le coordinate. Se aggiungo al comando [1] o [2] ho
# la 1ª o la 2ª coordinata. Per operare su curve vedi 27.
# Vedi qui per un esempio, che genera la figura seguente.
 # Tracciato un segmento o una freccia (con i comandi freccia, segm, linea, ...) le
# coordinate del punto finale sono memorizzate in xpunta e ypunta. La cosa può essere
# utile per costruire vari tipi di figure. Un punto inziale può essere tracciato con
# punticino: le sue coordinate sono messe in xpunta, ypunta. Vedi qui per un esempio,
# che genera la figura sopra a destra.
# punticino2 traccia invece un punto leggeremente più grande (3 pixel di diametro).
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
# Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
# Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# Se voglio mettere una scritta S su una parte con sfondo nel colore COLOR posso usare
# scriviC(x,y, COLOR, S) invece di scrivi(x,y, S)
# Per inserire un "a capo" posso inserire \n in S (vedi 16).
# Posso scrivere scritte ruotate col comando scriviR(x,y, Angolo, S) con Angolo in
# gradi e scritte ruotate e su sfondo colorato con scriviRC(x,y, Angolo, COLOR, S)
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# sottoassex(scritta), sottoassey(scritta) operano come suassex, suassey
# suAssex(scritta,x), suAssey(scritta,y), sottoAssex(…), sottoAssey(…)
# consentono di scegliere le coordinate in cui mettere le scritte
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
BF=4; HF=2.5
Griglia(1880,1980, 0,90) # Per Griglia vedi (15) di "es. uso di base":
# fa la griglia senza scritte lungo gli assi
spezzata(anni,frutta, "blue"); PUNTI(anni,frutta,"brown")
sottoassex("anni"); sottoassey("frutta")
sottoAssex("1880", 1880); sottoAssex("1980", 1980)
suAssey("90",90); suAssey("0",0); suAssey("50",50)
# Se la scritta invece che "frutta" è "90" posso fare a mano di mettere le virgolette:
# invece di suAssey("90",90) potrei mettere suAssey(90,90) o anche suAssey(9*10,90)
# Tracciato un segmento o una freccia (con i comandi freccia, segm, linea, ...) le
# coordinate del punto finale sono memorizzate in xpunta e ypunta. La cosa può essere
# utile per costruire vari tipi di figure. Un punto inziale può essere tracciato con
# punticino: le sue coordinate sono messe in xpunta, ypunta. Vedi qui per un esempio,
# che genera la figura sopra a destra.
# punticino2 traccia invece un punto leggeremente più grande (3 pixel di diametro).
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
# Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
# Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
# Se voglio mettere una scritta S su una parte con sfondo nel colore COLOR posso usare
# scriviC(x,y, COLOR, S) invece di scrivi(x,y, S)
# Per inserire un "a capo" posso inserire \n in S (vedi 16).
# Posso scrivere scritte ruotate col comando scriviR(x,y, Angolo, S) con Angolo in
# gradi e scritte ruotate e su sfondo colorato con scriviRC(x,y, Angolo, COLOR, S)
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
# sottoassex(scritta), sottoassey(scritta) operano come suassex, suassey
# suAssex(scritta,x), suAssey(scritta,y), sottoAssex(…), sottoAssey(…)
# consentono di scegliere le coordinate in cui mettere le scritte
anni <- c(1880,1890,1900,1910,1920,1930,1940,1950,1960,1970,1980)
frutta <- c(19,21,23,28,31,27,23,37,65,88,79)
BF=4; HF=2.5
Griglia(1880,1980, 0,90) # Per Griglia vedi (15) di "es. uso di base":
# fa la griglia senza scritte lungo gli assi
spezzata(anni,frutta, "blue"); PUNTI(anni,frutta,"brown")
sottoassex("anni"); sottoassey("frutta")
sottoAssex("1880", 1880); sottoAssex("1980", 1980)
suAssey("90",90); suAssey("0",0); suAssey("50",50)
# Se la scritta invece che "frutta" è "90" posso fare a mano di mettere le virgolette:
# invece di suAssey("90",90) potrei mettere suAssey(90,90) o anche suAssey(9*10,90)
 sottoassex2 scrive in una riga sottostante a quella usata da "sottoassex":
sottoassex2("kg di frutta all'anno consumati da un Italiano")
# Con la S maiuscola SuAssey e SottoAssey scrivono i numeri orizzontali.
n=c(90,0,50); for(i in 1:3) SuAssey(n[i],n[i])
sottoassex2 scrive in una riga sottostante a quella usata da "sottoassex":
sottoassex2("kg di frutta all'anno consumati da un Italiano")
# Con la S maiuscola SuAssey e SottoAssey scrivono i numeri orizzontali.
n=c(90,0,50); for(i in 1:3) SuAssey(n[i],n[i])
 # Il comando PianoP(x,y), dati dei punti con ascisse x e ordinate y, sceglie automatica-
# mente un "piano" che li contenga (è qualcosa di analogo a graficoF per le funzioni);
# PIANOP(x,y) lo sceglie monometrico. La cosa può essere comoda in molte situazioni.
# Vediamolo, per brevità, in questa:
PianoP(anni,frutta); spezzata(anni,frutta, "blue")
PIANOP(anni,frutta); spezzata(anni,frutta, "blue")
# Il comando PianoP(x,y), dati dei punti con ascisse x e ordinate y, sceglie automatica-
# mente un "piano" che li contenga (è qualcosa di analogo a graficoF per le funzioni);
# PIANOP(x,y) lo sceglie monometrico. La cosa può essere comoda in molte situazioni.
# Vediamolo, per brevità, in questa:
PianoP(anni,frutta); spezzata(anni,frutta, "blue")
PIANOP(anni,frutta); spezzata(anni,frutta, "blue")
 # 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm, TERMOMETRO
# Mentre torta, Torta, Tortam, Barre, Striscia scelgono automaticamente i colori
# con tortaC, TortaC, TortaM, StrisciaC, BarreC puoi aggiungere i colori.
da<- c(237.5,137.5,125); co<- c("red","yellow","blue")
nomiStriscia = c("A","B","C"); StrisciaC(da,co)
nomiBarre = c("A","B","C"); BarreC(da,co)
tortaC( da, c("grey50", "grey75", "grey95"))
# % 47.5 27.5 25
# 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm, TERMOMETRO
# Mentre torta, Torta, Tortam, Barre, Striscia scelgono automaticamente i colori
# con tortaC, TortaC, TortaM, StrisciaC, BarreC puoi aggiungere i colori.
da<- c(237.5,137.5,125); co<- c("red","yellow","blue")
nomiStriscia = c("A","B","C"); StrisciaC(da,co)
nomiBarre = c("A","B","C"); BarreC(da,co)
tortaC( da, c("grey50", "grey75", "grey95"))
# % 47.5 27.5 25
 # Il 2° diagramma a barre è stato ottenuto premettendo noGrglia=1.
# L'areogramma circolare a destra, in cui sono state aggiunte automaticamente delle
# lettere ai vari settori è stato ottenuto con Torta2C. Aggiungono automaticamente
# delle lettere anche torta2C, Torta2, torta2.
# Se nel grafico a barre voglio rappresentare i dati invece che le percentuali uso:
nomiBarre = c("A","B","C"); BARREC(da,co)
# ovvero (vedi l'uscita sotto a sinistra):
BARRE(da)
# giallo,celeste,... 237.5 137.5 125
# giallo,celeste,... % 47.5 27.5 25
# Il 2° diagramma a barre è stato ottenuto premettendo noGrglia=1.
# L'areogramma circolare a destra, in cui sono state aggiunte automaticamente delle
# lettere ai vari settori è stato ottenuto con Torta2C. Aggiungono automaticamente
# delle lettere anche torta2C, Torta2, torta2.
# Se nel grafico a barre voglio rappresentare i dati invece che le percentuali uso:
nomiBarre = c("A","B","C"); BARREC(da,co)
# ovvero (vedi l'uscita sotto a sinistra):
BARRE(da)
# giallo,celeste,... 237.5 137.5 125
# giallo,celeste,... % 47.5 27.5 25
 # Agli areogrammi circolari per semplicità i nomi sono assegnati automaticamente. Se
# devo distinguere vari areogrammi posso dar loro nomi diversi coi comandi Torta_C,
# torta_C, Torta_, torta_, analoghi ai comandi con 2 al posto di _, a cui aggiungo,
# dopo una virgola, un numero che indica il nome del primo settore: le lettere A,B,…,Z
# sono indicate dai numeri 1,2,…,26, le lettere a,b,…,z dai numeri 27,28,…,52.
da2 <- c(100,50,25); Torta_(da, 4); torta_C(da2,co, 27)
# % 47.5 27.5 25 % 57.14286 28.57143 14.28571
# Nota: È totalmente senza senso (anche se è usato da chi vuole ingannare il lettore)
# utilizzare areogrammi a settori circolari a forma di disco inclinato. Vedi qui.
# Usando BARRE2 è posso realizzare diagrammi a barre che non partono da 0: vedi qui.
# Agli areogrammi circolari per semplicità i nomi sono assegnati automaticamente. Se
# devo distinguere vari areogrammi posso dar loro nomi diversi coi comandi Torta_C,
# torta_C, Torta_, torta_, analoghi ai comandi con 2 al posto di _, a cui aggiungo,
# dopo una virgola, un numero che indica il nome del primo settore: le lettere A,B,…,Z
# sono indicate dai numeri 1,2,…,26, le lettere a,b,…,z dai numeri 27,28,…,52.
da2 <- c(100,50,25); Torta_(da, 4); torta_C(da2,co, 27)
# % 47.5 27.5 25 % 57.14286 28.57143 14.28571
# Nota: È totalmente senza senso (anche se è usato da chi vuole ingannare il lettore)
# utilizzare areogrammi a settori circolari a forma di disco inclinato. Vedi qui.
# Usando BARRE2 è posso realizzare diagrammi a barre che non partono da 0: vedi qui.
 # 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# Per avere altri percentili, dopo aver battuto altrestat(), puoi usare, ad es. per il
# 3° percentile, quantile(daticlas, 3/100). Con quantile(daticlas,1/2) hai la mediana.
# [ non aprire "daticlas": può contenere molti dati; eventualmente usa str(daticlass) ]
# Ma - sempre dopo aver battuto altrestat(), o dopo istogramma(…) - puoi più sempli-
# cemente battere: percentile(3)
#
# Posso confrontare boxplot relativi ad un dato fenomeno al passare, ad es., del tempo
# usando la stessa scala, assegnando l'intervallo in cui tracciare il boxplot a boxAB:
#
# altezze ventenni italiani maschi nel 1880 negli intervalli ampi 5 da 145 a 185 (cm)
# (tra 145 e 150 vi erano il 4% dei maschi, ...; sotto a 145 e sopra a 185
# le percentuali erano trascurabili)
freq1 <- c(4.0, 6.8, 20.4, 28.4, 23.5, 11.7, 3.7, 1.5)
interv1 <- seq(145,185, 5)
BF=4; HF=3; istoclas(interv1,freq1)
# ora dimensiono le finestre grafiche larghe e basse
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# altezze ventenni italiani maschi nel 1992 negli intervalli ampi 5 da 155 a 195 (cm)
freq2 <- c(1.7, 6.8, 18.6, 29.1, 25.2, 13.2, 4.3, 1.1)
interv2 <- seq(155,195, 5)
BF=4; HF=3; istoclas(interv2,freq2)
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# I boxplot ottenuti, a cui si sono aggiunte delle scritte:
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
# Per avere altri percentili, dopo aver battuto altrestat(), puoi usare, ad es. per il
# 3° percentile, quantile(daticlas, 3/100). Con quantile(daticlas,1/2) hai la mediana.
# [ non aprire "daticlas": può contenere molti dati; eventualmente usa str(daticlass) ]
# Ma - sempre dopo aver battuto altrestat(), o dopo istogramma(…) - puoi più sempli-
# cemente battere: percentile(3)
#
# Posso confrontare boxplot relativi ad un dato fenomeno al passare, ad es., del tempo
# usando la stessa scala, assegnando l'intervallo in cui tracciare il boxplot a boxAB:
#
# altezze ventenni italiani maschi nel 1880 negli intervalli ampi 5 da 145 a 185 (cm)
# (tra 145 e 150 vi erano il 4% dei maschi, ...; sotto a 145 e sopra a 185
# le percentuali erano trascurabili)
freq1 <- c(4.0, 6.8, 20.4, 28.4, 23.5, 11.7, 3.7, 1.5)
interv1 <- seq(145,185, 5)
BF=4; HF=3; istoclas(interv1,freq1)
# ora dimensiono le finestre grafiche larghe e basse
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# altezze ventenni italiani maschi nel 1992 negli intervalli ampi 5 da 155 a 195 (cm)
freq2 <- c(1.7, 6.8, 18.6, 29.1, 25.2, 13.2, 4.3, 1.1)
interv2 <- seq(155,195, 5)
BF=4; HF=3; istoclas(interv2,freq2)
BF=4; HF=1.4; boxAB=c(145,195); altrestat()
# I boxplot ottenuti, a cui si sono aggiunte delle scritte:
 # Gli istogrammi che si erano ottenuti con istoclass
# Gli istogrammi che si erano ottenuti con istoclass
 #
# Quando si hanno dati singoli che possono essere classificati in intervalli diversi
# può essere comodo rappresentarli con un istogramma di area 1, in modo che l'area di
# ogni colonnina corrisponda alla frequenza relativa di essa, come abbiamo visto si
# fa per i dati già classificati in intervalli (vedi qui). Per far questo si ricorre
# al comando hist. Ecco qualche esempio d'uso relativamente alle fave considerate nella
# prima parte di questo documento. dev.new() serve per aprire una nuova finestra,
# abline per tracciare linee parallele agli assi. Il numero delle classi viene scelto
# automaticamente o può essere precisato, approssimativamente, con nclass. Con cex.axis
# posso dimensionare i caratteri. right=FALSE specifica che gli intervalli in cui sono
# classificati i dati sono del tipo […,…).
# L'essenziale è: hist(fave, right=FALSE, probability=TRUE).
# "Density" indica che sull'asse y è rappresentata la densità di frequenza, ossia la
# frequenza percentuale unitaria (invece di probability=TRUE posso usare freq=FALSE).
dev.new()
hist(fave, nclass=5, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey")
abline(h=axTicks(2),lty=3)
# e quello che ottengo con nclass=20 e con nclass=10 (o senza specificare nclass)
#
# Quando si hanno dati singoli che possono essere classificati in intervalli diversi
# può essere comodo rappresentarli con un istogramma di area 1, in modo che l'area di
# ogni colonnina corrisponda alla frequenza relativa di essa, come abbiamo visto si
# fa per i dati già classificati in intervalli (vedi qui). Per far questo si ricorre
# al comando hist. Ecco qualche esempio d'uso relativamente alle fave considerate nella
# prima parte di questo documento. dev.new() serve per aprire una nuova finestra,
# abline per tracciare linee parallele agli assi. Il numero delle classi viene scelto
# automaticamente o può essere precisato, approssimativamente, con nclass. Con cex.axis
# posso dimensionare i caratteri. right=FALSE specifica che gli intervalli in cui sono
# classificati i dati sono del tipo […,…).
# L'essenziale è: hist(fave, right=FALSE, probability=TRUE).
# "Density" indica che sull'asse y è rappresentata la densità di frequenza, ossia la
# frequenza percentuale unitaria (invece di probability=TRUE posso usare freq=FALSE).
dev.new()
hist(fave, nclass=5, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey")
abline(h=axTicks(2),lty=3)
# e quello che ottengo con nclass=20 e con nclass=10 (o senza specificare nclass)
 # Se vuoi aggiungere un istogramma in una pagina grafica aperta aggiungi alle opzioni
# ,add=TRUE Se non vuoi colorare la parte interna non mettere ,col=… Se vuoi colorare
# diversamente il bordo aggiungi ,border=… Per altro vedi gli approfondimenti.
# Per consoscere l'altezza di un istogramma (la densità massima), ad es. nel 1º caso:
max( hist(fave, nclass=5, right=FALSE, probability=TRUE, plot=FALSE)$density )
# 2.461538
# Ricordiamo che i valori di media e percentili relativi a dati non già classificati
# hanno senso solo se i dati sono arrotondati. Se ad es. ho dati troncati agli interi
# devo prima trasformarli aggiungendo 1/2 (dati = dati+1/2); se sono troncati ai decimi
# devo aggiungere 1/2 decimo (dati = dati+0.1/2); se sono troncati alle centininaia
# devo aggiungere 1/2 centinaia (dati = dati+100/2).
# Per simulare (con runif e sample, e set.seed) fenomeni e analizzare problemi probabi-
# listici (uso di Var, Sd, SdM, studio della gaussiana ed altre distribuzioni), e per
# (de)codificare messaggi, vedi gli approfondimenti (verso il fondo).
# Approfondimenti QUI
# Col comando analisiTesto(testo) posso analizzare statisticamente testi. Vedi qui come
# usare il comando (e le variabili maxIsto e maxIstoN, impiegabili per confrontare nella
# stessa scala istogrammi di fenomeni diversi). Sotto alcune delle uscite ottenibili
# confrontando lo stesso brano di "Alice nel paese delle meraviglie" in italiano e in
# inglese.
# Se vuoi aggiungere un istogramma in una pagina grafica aperta aggiungi alle opzioni
# ,add=TRUE Se non vuoi colorare la parte interna non mettere ,col=… Se vuoi colorare
# diversamente il bordo aggiungi ,border=… Per altro vedi gli approfondimenti.
# Per consoscere l'altezza di un istogramma (la densità massima), ad es. nel 1º caso:
max( hist(fave, nclass=5, right=FALSE, probability=TRUE, plot=FALSE)$density )
# 2.461538
# Ricordiamo che i valori di media e percentili relativi a dati non già classificati
# hanno senso solo se i dati sono arrotondati. Se ad es. ho dati troncati agli interi
# devo prima trasformarli aggiungendo 1/2 (dati = dati+1/2); se sono troncati ai decimi
# devo aggiungere 1/2 decimo (dati = dati+0.1/2); se sono troncati alle centininaia
# devo aggiungere 1/2 centinaia (dati = dati+100/2).
# Per simulare (con runif e sample, e set.seed) fenomeni e analizzare problemi probabi-
# listici (uso di Var, Sd, SdM, studio della gaussiana ed altre distribuzioni), e per
# (de)codificare messaggi, vedi gli approfondimenti (verso il fondo).
# Approfondimenti QUI
# Col comando analisiTesto(testo) posso analizzare statisticamente testi. Vedi qui come
# usare il comando (e le variabili maxIsto e maxIstoN, impiegabili per confrontare nella
# stessa scala istogrammi di fenomeni diversi). Sotto alcune delle uscite ottenibili
# confrontando lo stesso brano di "Alice nel paese delle meraviglie" in italiano e in
# inglese.
 # 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
# Oltre che grafici di funzioni di una variabile posso tracciare curve descritte come
# funzioni di due variabili, K(x,y)=0, mediante il comando curva(K, col). Esempi:
PIANO(-5,5, -5,5)
f <- function(x,y) y-(x^2-3); curva(f, "red")
g <- function(x,y) x-(y^2-3); curva(g, "blue")
h <- function(x,y) x^2+y^2-16; curva(h, "violet")
k <- function(x,y) x*y-1; cur(k, "black")
# Per altri modi di descrivere curve vedi qui [le coniche] e sotto il punto 27.
# Per risolvere eq. del tipo F(x,y)=0 rispetto ad x (fissato y=k) o ad y (fissato x=k)
# vedi qui.
# cur traccia le curve sottili.
# Analogamente graficF e grafic operano come graficoF e grafico ma con linee sottili
# grafiF e grafi le fanno di uno spessore intermedio
Piano(-5,5, -5,15)
q <- function(x) x^2-4; grafico(q,-5,5, "blue")
s <- function(x) x^2-2; grafic(s,-5,0, "red"); grafi(s,0,5, "seagreen")
# f, g, h, k q, s
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
# Oltre che grafici di funzioni di una variabile posso tracciare curve descritte come
# funzioni di due variabili, K(x,y)=0, mediante il comando curva(K, col). Esempi:
PIANO(-5,5, -5,5)
f <- function(x,y) y-(x^2-3); curva(f, "red")
g <- function(x,y) x-(y^2-3); curva(g, "blue")
h <- function(x,y) x^2+y^2-16; curva(h, "violet")
k <- function(x,y) x*y-1; cur(k, "black")
# Per altri modi di descrivere curve vedi qui [le coniche] e sotto il punto 27.
# Per risolvere eq. del tipo F(x,y)=0 rispetto ad x (fissato y=k) o ad y (fissato x=k)
# vedi qui.
# cur traccia le curve sottili.
# Analogamente graficF e grafic operano come graficoF e grafico ma con linee sottili
# grafiF e grafi le fanno di uno spessore intermedio
Piano(-5,5, -5,15)
q <- function(x) x^2-4; grafico(q,-5,5, "blue")
s <- function(x) x^2-2; grafic(s,-5,0, "red"); grafi(s,0,5, "seagreen")
# f, g, h, k q, s
 #
# NOTA. I comandi grafico e graficoF impiegano abbastanza tempo a tracciare i grafici
# delle funzioni ad 1 input ma li fanno precisi. Vedi qui per prestare attenzione all'
# uso del comando curva e del comando plot (che non abbiamo discusso finora). Nella
# figura seguente vedi i grafici corretti di alcune funzioni che presentano dei salti
# ottenuti con grafico e quelli scorretti ottenuti con curva e con plot.
#
# NOTA. I comandi grafico e graficoF impiegano abbastanza tempo a tracciare i grafici
# delle funzioni ad 1 input ma li fanno precisi. Vedi qui per prestare attenzione all'
# uso del comando curva e del comando plot (che non abbiamo discusso finora). Nella
# figura seguente vedi i grafici corretti di alcune funzioni che presentano dei salti
# ottenuti con grafico e quelli scorretti ottenuti con curva e con plot.
 #
# Abbiamo visto come calcolare la distanza di un punto da un altro punto o una retta.
# Il comando distPF(x,y, F, a,b) calcola la distanza tra un punto x,y e il grafico di
# una funzione F ad 1 input e 1 output nel dominio a,b.
# Vediamo ad es. come calcolare le distanze seguenti, di (2,0) - punto blu - da K e G
# (voglio capire quale delle due curve è più vicina al punto):
#
# Abbiamo visto come calcolare la distanza di un punto da un altro punto o una retta.
# Il comando distPF(x,y, F, a,b) calcola la distanza tra un punto x,y e il grafico di
# una funzione F ad 1 input e 1 output nel dominio a,b.
# Vediamo ad es. come calcolare le distanze seguenti, di (2,0) - punto blu - da K e G
# (voglio capire quale delle due curve è più vicina al punto):
 PIANO(-1,2, -1,2)
K <- function(x) 2*x-0.5; grafico(K,-1,2, "red")
G <- function(x) x^2; grafico(G,-1,2, "brown")
PUNTO(2,-1, "blue"); distPF(2,-1, K, -1,2)
distanza e punto più vicino:
# 2.012461 0.200000 -0.100000
PUNTO(0.2,-0.1, "black"); linea(0.2,-0.1, 2,-1, "blue")
# in questo caso la distanza l'avrei trovata anche col comando punto_retta
punto_retta(2,-1, 0,-1/2, 1,1.5)
# 2.012461
# Per G, che non ha come grafico una retta non posso farlo
distPF(2,-1, G, -1,2)
distanza e punto più vicino:
# 1.9490881 0.5535740 0.3064442
# Posso migliorare la precisione partendo da un intervallo più piccolo
distPF(2,-1, G, 0.5,0.6)
# 1.9490881 0.5535738 0.3064440
PUNTO(0.5535740, 0.3064442, 1); linea(0.5535740, 0.3064442, 2,-1, "blue")
# È più vicina la curva G
# Calcoliamo la distanza del punto rosso, (0,1), da G:
PUNTO(0,1, "red"); distPF(0,1, G, -1,2)
# 0.8660254 -0.7071070 0.5000003 Miglioro la precisione:
distPF(0,1, G, -0.8,-0.6)
# 0.8660254 -0.7071068 0.5000000 Oltre a 0.866... anche 0.707… e 0.5 mi
# sembrano delle radici quadrate di frazioni tra interi. Verifico:
frazio(distPF(0,1, G, -0.8,-0.6)^2)
# 0.8660254 -0.7071068 0.5000000
# 3/4 1/2 1/4 La distanza è √3/2
# Traccio (0.707…, 0.5)
PUNTO(sqrt(1/2), 1/2, "seagreen"); linea(0,1, sqrt(1/2),1/2, "blue")
#
# NOTA: curva(h,...) per fare il grafico di h(x,y)=0 cerca dove h cambia
# segno; se ovunque h(x,y)≥0 o h(x,y)≤0 il grafico non viene tracciato.
# Prova allora a fare quello di abs(h(x,y))-eps = 0 con eps piccolo.
# Un esempio facile, per capire:
PIANO(-4,4, -4,4)
g <- function(x,y) x^2+4*y^2-4*x*y; curva(g,"green")
# non ottengo nulla ( anche se in questo caso so che la curva
# è x-2*y = 0 in quanto x^2+4*y^2-4*x*y = (x-2*y)^2 )
eps <- 1e-4; k <- function(x,y) abs(g(x,y))-eps; curva(k,"blue")
PIANO(-1,2, -1,2)
K <- function(x) 2*x-0.5; grafico(K,-1,2, "red")
G <- function(x) x^2; grafico(G,-1,2, "brown")
PUNTO(2,-1, "blue"); distPF(2,-1, K, -1,2)
distanza e punto più vicino:
# 2.012461 0.200000 -0.100000
PUNTO(0.2,-0.1, "black"); linea(0.2,-0.1, 2,-1, "blue")
# in questo caso la distanza l'avrei trovata anche col comando punto_retta
punto_retta(2,-1, 0,-1/2, 1,1.5)
# 2.012461
# Per G, che non ha come grafico una retta non posso farlo
distPF(2,-1, G, -1,2)
distanza e punto più vicino:
# 1.9490881 0.5535740 0.3064442
# Posso migliorare la precisione partendo da un intervallo più piccolo
distPF(2,-1, G, 0.5,0.6)
# 1.9490881 0.5535738 0.3064440
PUNTO(0.5535740, 0.3064442, 1); linea(0.5535740, 0.3064442, 2,-1, "blue")
# È più vicina la curva G
# Calcoliamo la distanza del punto rosso, (0,1), da G:
PUNTO(0,1, "red"); distPF(0,1, G, -1,2)
# 0.8660254 -0.7071070 0.5000003 Miglioro la precisione:
distPF(0,1, G, -0.8,-0.6)
# 0.8660254 -0.7071068 0.5000000 Oltre a 0.866... anche 0.707… e 0.5 mi
# sembrano delle radici quadrate di frazioni tra interi. Verifico:
frazio(distPF(0,1, G, -0.8,-0.6)^2)
# 0.8660254 -0.7071068 0.5000000
# 3/4 1/2 1/4 La distanza è √3/2
# Traccio (0.707…, 0.5)
PUNTO(sqrt(1/2), 1/2, "seagreen"); linea(0,1, sqrt(1/2),1/2, "blue")
#
# NOTA: curva(h,...) per fare il grafico di h(x,y)=0 cerca dove h cambia
# segno; se ovunque h(x,y)≥0 o h(x,y)≤0 il grafico non viene tracciato.
# Prova allora a fare quello di abs(h(x,y))-eps = 0 con eps piccolo.
# Un esempio facile, per capire:
PIANO(-4,4, -4,4)
g <- function(x,y) x^2+4*y^2-4*x*y; curva(g,"green")
# non ottengo nulla ( anche se in questo caso so che la curva
# è x-2*y = 0 in quanto x^2+4*y^2-4*x*y = (x-2*y)^2 )
eps <- 1e-4; k <- function(x,y) abs(g(x,y))-eps; curva(k,"blue")
 # Posso provare a fare automaticamente ciò col comando seguente ("n" sta per nulla):
curvan(g,1,"red") # o curvan(g,N,col) con N > 1 o < 1, o curn per una curva sottile
#
# Posso tracciare griglie e indicare le scale in forma non decimale. Questo può essere
# utile, ad esempio, nel caso di funzioni trigonometriche, ma non solo. Si possono
# indicare le distanze tra i lati della griglia coi comandi TACCHEx e TACCHEy e usare
# i comandi Piano2 o PIANO2 per tracciare la parte di piano cartesiano voluta. Vedi
# qui per ottenere grafici come il seguente:
# Posso provare a fare automaticamente ciò col comando seguente ("n" sta per nulla):
curvan(g,1,"red") # o curvan(g,N,col) con N > 1 o < 1, o curn per una curva sottile
#
# Posso tracciare griglie e indicare le scale in forma non decimale. Questo può essere
# utile, ad esempio, nel caso di funzioni trigonometriche, ma non solo. Si possono
# indicare le distanze tra i lati della griglia coi comandi TACCHEx e TACCHEy e usare
# i comandi Piano2 o PIANO2 per tracciare la parte di piano cartesiano voluta. Vedi
# qui per ottenere grafici come il seguente:
 # 23 Risolvere equazioni (soluz).
# Se hai un'equazione del tipo F(x)=G(x) puoi risolverla definendo H come F-G e usando
# soluz. Ma puoi più anche usare soluz2(F,G, a,b) se la soluzione è tra a e b:
f <- function(x) x^2-2; g <- function(x) x^3+1
graficoF(f, -3,3, "blue"); grafico(g, -3,3, "brown")
x <- soluz2(f,g, -2,0); x; piu(x); punto(x,f(x), "red")
# -1.174559 -1.17455941029298
# 23 Risolvere equazioni (soluz).
# Se hai un'equazione del tipo F(x)=G(x) puoi risolverla definendo H come F-G e usando
# soluz. Ma puoi più anche usare soluz2(F,G, a,b) se la soluzione è tra a e b:
f <- function(x) x^2-2; g <- function(x) x^3+1
graficoF(f, -3,3, "blue"); grafico(g, -3,3, "brown")
x <- soluz2(f,g, -2,0); x; piu(x); punto(x,f(x), "red")
# -1.174559 -1.17455941029298
 # Puoi anche ricorrere a WolframAlpha, ma le uscite non sono sempre facili da
# interpretare: vedi.
#
# Puoi risolvere le equazioni polinomiali in cui l'unica variabile che compare è l'
# incognita: soluzione di -78 + 73*x - 57*x^2 + 73*x^3 + 21*x^4 = 0
# ( occorre mettere i coefficienti per grado crescente )
q <- c(-78, 73, -57, 73, 21); solpol(q)
# 0.857142857142857 -4.33333333333333
# Le uscite sono temporaneamente messe in soluzione
a = soluzione[1]; b = soluzione[2]; a; piu( b)
# 0.8571429 -4.33333333333333
frazio( soluzione )
# 6/7 -13/3
# Controllo grafico (vedi sotto a sinistra):
f <- function(x) -78+73*x-57*x^2+73*x^3+21*x^4
graficoF(f, -5,2, "blue")
# Puoi anche ricorrere a WolframAlpha, ma le uscite non sono sempre facili da
# interpretare: vedi.
#
# Puoi risolvere le equazioni polinomiali in cui l'unica variabile che compare è l'
# incognita: soluzione di -78 + 73*x - 57*x^2 + 73*x^3 + 21*x^4 = 0
# ( occorre mettere i coefficienti per grado crescente )
q <- c(-78, 73, -57, 73, 21); solpol(q)
# 0.857142857142857 -4.33333333333333
# Le uscite sono temporaneamente messe in soluzione
a = soluzione[1]; b = soluzione[2]; a; piu( b)
# 0.8571429 -4.33333333333333
frazio( soluzione )
# 6/7 -13/3
# Controllo grafico (vedi sotto a sinistra):
f <- function(x) -78+73*x-57*x^2+73*x^3+21*x^4
graficoF(f, -5,2, "blue")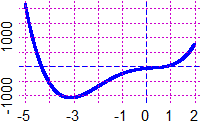
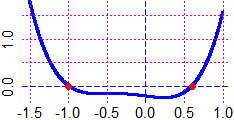
 ## PARTI NUOVE
# 24 Calcolo approssimato
# (vedi il punto 31 per la rappresentazione grafica delle approssimazioni)
#
## PARTI NUOVE
# 24 Calcolo approssimato
# (vedi il punto 31 per la rappresentazione grafica delle approssimazioni)
#  # Se poi voglio vedere griglia e assi basta che batta BOX(), che li sovrappone alla
# immagine che compare nell'ultima finestra grafica. BOXs() la traccia senza assi,
# BOXg() la traccia con gli assi più grandi, ossia più spessi.
# Qui puoi vederne un altro esempio.
# Se poi voglio vedere griglia e assi basta che batta BOX(), che li sovrappone alla
# immagine che compare nell'ultima finestra grafica. BOXs() la traccia senza assi,
# BOXg() la traccia con gli assi più grandi, ossia più spessi.
# Qui puoi vederne un altro esempio.
 # Per una "quasi" animazione, batti Quadrilatero(a,b,c,d) dove al posto di a,b,c,d
# metti le direzioni in cui sono posti i vertici (in °, tra 0 e 360)
# Per una "quasi" animazione, batti Quadrilatero(a,b,c,d) dove al posto di a,b,c,d
# metti le direzioni in cui sono posti i vertici (in °, tra 0 e 360)
 # [ la prima figura è stata ottenuta con Quadrilatero(0,80,195.67,286) ]
# [PianoN e PIANON operano in modo simile a BoxN e BoxmN]
# Per animazioni in cui vi siano assi e coordinate convengono i comandi recordPlot e
# replayPlot visti in 12. Vedi qui per un esempio. Vedi anche Esempi-27.
# Per relizzare animazioni con sistemi di riferimento che mutano puoi usare dev.off()
# e dev.new() che, rispettivamente, chiudono l'ultima finestra e ne aprono una nuova.
# NF() predispone una nuova finestra delle stesse dimensioni dell'ultima usata.
# PPP() memorizza come xP e yP le coord. del punto cliccato
# puntiB, puntiniB, punticiniB, palliniB scelgono automaticamente il box,
# puntiBm, puntiniBm, punticiniBm, palliniBm lo scelgono monometrico.
# Spezzata e Spezza a differenza di spezzata e spezza non connettono le "y".
# spezzat opera come spezza ma tratteggia i segmenti.
# Spezzat opera come spezza ma fa i segmenti un po' più spessi.
BF <- 2; HF <- 2; x <- c(0,2,3,6); y <- c(1,2,4,5)
PIANO(0,6,0,6); spezzata(x,y, "blue"); PIANO(0,6,0,6); Spezzata(x,y, "blue")
PIANO(0,6,0,6); spezzat(x,y, "red"); PIANO(0,6,0,6); Spezzat(x,y, "seagreen")
# [ la prima figura è stata ottenuta con Quadrilatero(0,80,195.67,286) ]
# [PianoN e PIANON operano in modo simile a BoxN e BoxmN]
# Per animazioni in cui vi siano assi e coordinate convengono i comandi recordPlot e
# replayPlot visti in 12. Vedi qui per un esempio. Vedi anche Esempi-27.
# Per relizzare animazioni con sistemi di riferimento che mutano puoi usare dev.off()
# e dev.new() che, rispettivamente, chiudono l'ultima finestra e ne aprono una nuova.
# NF() predispone una nuova finestra delle stesse dimensioni dell'ultima usata.
# PPP() memorizza come xP e yP le coord. del punto cliccato
# puntiB, puntiniB, punticiniB, palliniB scelgono automaticamente il box,
# puntiBm, puntiniBm, punticiniBm, palliniBm lo scelgono monometrico.
# Spezzata e Spezza a differenza di spezzata e spezza non connettono le "y".
# spezzat opera come spezza ma tratteggia i segmenti.
# Spezzat opera come spezza ma fa i segmenti un po' più spessi.
BF <- 2; HF <- 2; x <- c(0,2,3,6); y <- c(1,2,4,5)
PIANO(0,6,0,6); spezzata(x,y, "blue"); PIANO(0,6,0,6); Spezzata(x,y, "blue")
PIANO(0,6,0,6); spezzat(x,y, "red"); PIANO(0,6,0,6); Spezzat(x,y, "seagreen")
 puntiB(x,y, "red"); puntiBm(x,y, "red")
puntiB(x,y, "red"); puntiBm(x,y, "red")


 # Sopra come è possibile tracciare altri tipi di punti ("D" come "Delta"):
PIANO(0,6,0,6); puntoO(1,1,"blue"); puntoV(3,3,"red"); puntoD(4,2,"black")
# puntiO/V/D(x,y,col) se sono messi in x,y più punti, non li collegano
# Linea e LInea a differenza di linea, che traccia i segmenti come segm ma sottili,
# tratteggiano i segmenti (con tratto corto/lungo).
# Con centroPol(x,y) ho il centroide del poligono "x,y" (vedi sopra figura a destra).
BF <- 2; HF <- 2; x <- c(1,4,5,1); y <- c(1,0,5,4)
PIANO(0,6,0,6); spezzaC(x,y,"green"); Linea(1,4, 4,0, "red"); LInea(1,1, 5,5, "blue")
centroPol(x,y); PUNTI(centroPol(x,y)[1],centroPol(x,y)[2],"brown")
# [1] 2.904762 2.571429
# Nel caso di masse isolate m1, m2, … posizionate nei punti x1,y1, x2,y2, …, posto
# m = c(m1,m2,…), x = c(x1,x2,…), y = c(y1,y2,…), le coordinate del baricentro sono:
sum(m*x)/sum(m); sum(m*y)/sum(m)
# Sopra come è possibile tracciare altri tipi di punti ("D" come "Delta"):
PIANO(0,6,0,6); puntoO(1,1,"blue"); puntoV(3,3,"red"); puntoD(4,2,"black")
# puntiO/V/D(x,y,col) se sono messi in x,y più punti, non li collegano
# Linea e LInea a differenza di linea, che traccia i segmenti come segm ma sottili,
# tratteggiano i segmenti (con tratto corto/lungo).
# Con centroPol(x,y) ho il centroide del poligono "x,y" (vedi sopra figura a destra).
BF <- 2; HF <- 2; x <- c(1,4,5,1); y <- c(1,0,5,4)
PIANO(0,6,0,6); spezzaC(x,y,"green"); Linea(1,4, 4,0, "red"); LInea(1,1, 5,5, "blue")
centroPol(x,y); PUNTI(centroPol(x,y)[1],centroPol(x,y)[2],"brown")
# [1] 2.904762 2.571429
# Nel caso di masse isolate m1, m2, … posizionate nei punti x1,y1, x2,y2, …, posto
# m = c(m1,m2,…), x = c(x1,x2,…), y = c(y1,y2,…), le coordinate del baricentro sono:
sum(m*x)/sum(m); sum(m*y)/sum(m)

 # 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
Puoi tracciare curve in forma parametrica battendo:
param(X,Y, a,b, col) se hai già definito 2 funz. X e Y di un parametro
che varia tra a e b, o in forma polare con:
polar(R, a,b, col) se hai def. R funz. dell'angolo tra a e b.
Es.: le seguenti istruzioni tracciano un'ellisse:
PIANO(-2,2,-2,2)
f <- function(t) 2*cos(t); g <- function(t) sin(t); param(f,g,0,2*pi,'red')
e queste una spirale
PIANO(-5,5,-5,5); r <- function(a) sqrt(a); polar(r,0,20,'blue')
Con para() par1() pola() pol1() si ha uno spessore minore
paramb, polarb, …, pol1b scelgono anche il box, monometrico
# 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
Puoi tracciare curve in forma parametrica battendo:
param(X,Y, a,b, col) se hai già definito 2 funz. X e Y di un parametro
che varia tra a e b, o in forma polare con:
polar(R, a,b, col) se hai def. R funz. dell'angolo tra a e b.
Es.: le seguenti istruzioni tracciano un'ellisse:
PIANO(-2,2,-2,2)
f <- function(t) 2*cos(t); g <- function(t) sin(t); param(f,g,0,2*pi,'red')
e queste una spirale
PIANO(-5,5,-5,5); r <- function(a) sqrt(a); polar(r,0,20,'blue')
Con para() par1() pola() pol1() si ha uno spessore minore
paramb, polarb, …, pol1b scelgono anche il box, monometrico
 Esempi - 41
# 42 Escher
Tassellazioni di Escher: escher()
Esempi - 42
# 43 Struttura dei termini
Visalizzazione della struttura dei termini
Esempi - 43
# 44 Grafi ad albero
Esempi - 44
# 45 Altre immagini
Esempi - 45
Oltre alle immagini animate come quelle viste in 25 e 27, si possono costruire
file html animati come questo nel modo spiegato qui. Per scaricare la cartella
contenente l'esempio e le spiegazioni clicca qui.
------------------------------------------------------------------
Esempi - 27 (vedi)
PIANO(-60,60, -60,60)
ro1 <- function(a) a^1.5
polar(ro1,0,5*pi, "red")
ro2 <- function(a) 30/(2+sin(a)-cos(a))
polar(ro2,0,5*pi, "green")
asc1 <- function(t) 2*t^2-3*t
ord1 <- function(t) t^3-t+1
param(asc1, ord1, -10,10, "blue")
asc2 <- function(t) -30+20*cos(t)
ord2 <- function(t) 10+30*sin(t)
param(asc2, ord2, 0,2*pi, "magenta")
H <- function(x,y) x*y-100
curva(H, "grey")
rottramo(H, 45, 0,0, 1.5,1, "black")
#
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, "blue")
punto(4,3, "red"); moltrarot(F, 8,4, 4,3, -30, "blue")
# figura a destra:
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, -1); C1 = ZZZ
PUNTO(4,3, "magenta"); moltrarot(F, 8,4, 4,3, -30, "blue")
moltrarot(C1, 1,1, 0,2, 0, "red"); moltrarot(C1, 1/2,1/2, 0,2, 0, "grey")
Esempi - 41
# 42 Escher
Tassellazioni di Escher: escher()
Esempi - 42
# 43 Struttura dei termini
Visalizzazione della struttura dei termini
Esempi - 43
# 44 Grafi ad albero
Esempi - 44
# 45 Altre immagini
Esempi - 45
Oltre alle immagini animate come quelle viste in 25 e 27, si possono costruire
file html animati come questo nel modo spiegato qui. Per scaricare la cartella
contenente l'esempio e le spiegazioni clicca qui.
------------------------------------------------------------------
Esempi - 27 (vedi)
PIANO(-60,60, -60,60)
ro1 <- function(a) a^1.5
polar(ro1,0,5*pi, "red")
ro2 <- function(a) 30/(2+sin(a)-cos(a))
polar(ro2,0,5*pi, "green")
asc1 <- function(t) 2*t^2-3*t
ord1 <- function(t) t^3-t+1
param(asc1, ord1, -10,10, "blue")
asc2 <- function(t) -30+20*cos(t)
ord2 <- function(t) 10+30*sin(t)
param(asc2, ord2, 0,2*pi, "magenta")
H <- function(x,y) x*y-100
curva(H, "grey")
rottramo(H, 45, 0,0, 1.5,1, "black")
#
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, "blue")
punto(4,3, "red"); moltrarot(F, 8,4, 4,3, -30, "blue")
# figura a destra:
PIANO(-8,12, -5,9)
F <- function(x,y) x^2+y^2-1; curva(F,"brown")
moltrarot(F, 8,4, 0,0, 0, -1); C1 = ZZZ
PUNTO(4,3, "magenta"); moltrarot(F, 8,4, 4,3, -30, "blue")
moltrarot(C1, 1,1, 0,2, 0, "red"); moltrarot(C1, 1/2,1/2, 0,2, 0, "grey")
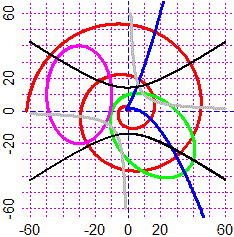
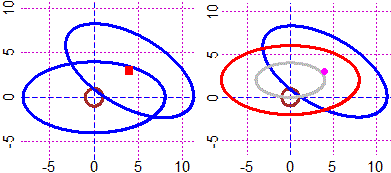
 Esempi - 28 (vedi)
## Il calcolo di x*(10+x)+5*x^3 per x=123456789012345
x <- "123456789012345"
som( pro(x, som(10,x)), pro(5, pro(x, pro(x,x))))
# "9408381861768148891412848380186556157340600"
## Verifica. Batto il numero e ottengo la rappr. esponenziale:
9408381861768148891412848380186556157340600
# 9.408382e+42
## Cosa otterremmo direttamente:
x <- 123456789012345; x*(10+x)+5*x^3; piu(ultimo())
# 9.408382e+42 9.40838186176815e+42
#
## 40!
n <- 40; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "815915283247897734345611269596115894272000000000"
## 171!
n <- 171; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "1241018070217667823424840524103103992616605577501693185388951803
6119960752216917529927519781204875855764649595016703870528098898
5869071076733124203221848436431047357788996854827829075454156196
4852153468318044293239598173696899657235903947616152278558180061
176365108428800000000000000000000000000000000000000000"
## Un trucco per stampare una stringa lunga su più righe:
str <- z; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "12410180702176678234248405241031039926166055775016931853889518036119960752216917"
# "52992751978120487585576464959501670387052809889858690710767331242032218484364310"
# "47357788996854827829075454156196485215346831804429323959817369689965723590394761"
# "6152278558180061176365108428800000000000000000000000000000000000000000"
#
## 2^1024, non calcolabile direttamente
2^1023; 2^1024
# 8.988466e+307 Inf
## Col programma per 2^1024 ottengo:
y <- 1; for(i in 1:1024) y <- pro(y,2)
str <- y; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "17976931348623159077293051907890247336179769789423065727343008115773267580550096"
"31327084773224075360211201138798713933576587897688144166224928474306394741243777"
"67893424865485276302219601246094119453082952085005768838150682342462881473913110"
"7237163350510684586298239947245938479716304835356329624224137216"
## nchar(y) -> 309 Sono 309 cifre (quelle di 2^1023 erano 308)
#
## Approssimazione in notazione scientifica
x <- "12345678901234567890"; app(x)
# 1.234568e+19
#
## 1000^20-999^20
y <- 1; for(i in 1:20) y <- pro(y,999)
z <- 1; for(i in 1:20) z <- pro(z,1000)
dif(z,y)
# "19811135170465317394197775411834107481255499156139810019999"
app(z); app(y); app(dif(z,y))
# 1e+60 9.801889e+59 1.981114e+58
#
## Stringhe <-> Numeri
N <- NUMERO(137); S <- substr(N,2,3); S; nchar(S); strtoi(paste0(S,"0",S))
# "37" 2 37037
## Numeri romani
as.roman(1944)
# MCMXLIV
## Rapporti < 1 in basi varie (4/100 in base 2, 55 cifre)
MNB(4,100, 2,55)
# 0. 0 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0
# 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 resto 36
Esempi - 29 (vedi)
F <- function(x) x*(x-2); G <- function(x) x/2
graficoF(F,-1,3, "blue"); grafico(G,-1,3, "red")
# vedi i grafici sotto a sinistra
diseq(F,G,-1,3,"black")
diseq(F,G,-1,3,"black")
diseq(G,F,-1,3,"orange")
diseq(G,F,-1,3,"orange")
Esempi - 28 (vedi)
## Il calcolo di x*(10+x)+5*x^3 per x=123456789012345
x <- "123456789012345"
som( pro(x, som(10,x)), pro(5, pro(x, pro(x,x))))
# "9408381861768148891412848380186556157340600"
## Verifica. Batto il numero e ottengo la rappr. esponenziale:
9408381861768148891412848380186556157340600
# 9.408382e+42
## Cosa otterremmo direttamente:
x <- 123456789012345; x*(10+x)+5*x^3; piu(ultimo())
# 9.408382e+42 9.40838186176815e+42
#
## 40!
n <- 40; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "815915283247897734345611269596115894272000000000"
## 171!
n <- 171; y <- 0;z <- 1;j <- 1; while(j<=n){y<- som(y,1); z<- pro(z,y); j<-j+1}; z
# "1241018070217667823424840524103103992616605577501693185388951803
6119960752216917529927519781204875855764649595016703870528098898
5869071076733124203221848436431047357788996854827829075454156196
4852153468318044293239598173696899657235903947616152278558180061
176365108428800000000000000000000000000000000000000000"
## Un trucco per stampare una stringa lunga su più righe:
str <- z; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "12410180702176678234248405241031039926166055775016931853889518036119960752216917"
# "52992751978120487585576464959501670387052809889858690710767331242032218484364310"
# "47357788996854827829075454156196485215346831804429323959817369689965723590394761"
# "6152278558180061176365108428800000000000000000000000000000000000000000"
#
## 2^1024, non calcolabile direttamente
2^1023; 2^1024
# 8.988466e+307 Inf
## Col programma per 2^1024 ottengo:
y <- 1; for(i in 1:1024) y <- pro(y,2)
str <- y; col <- 80; for(n in 0:(nchar(str)/col)) print(substr(str,n*col+1,(n+1)*col))
# "17976931348623159077293051907890247336179769789423065727343008115773267580550096"
"31327084773224075360211201138798713933576587897688144166224928474306394741243777"
"67893424865485276302219601246094119453082952085005768838150682342462881473913110"
"7237163350510684586298239947245938479716304835356329624224137216"
## nchar(y) -> 309 Sono 309 cifre (quelle di 2^1023 erano 308)
#
## Approssimazione in notazione scientifica
x <- "12345678901234567890"; app(x)
# 1.234568e+19
#
## 1000^20-999^20
y <- 1; for(i in 1:20) y <- pro(y,999)
z <- 1; for(i in 1:20) z <- pro(z,1000)
dif(z,y)
# "19811135170465317394197775411834107481255499156139810019999"
app(z); app(y); app(dif(z,y))
# 1e+60 9.801889e+59 1.981114e+58
#
## Stringhe <-> Numeri
N <- NUMERO(137); S <- substr(N,2,3); S; nchar(S); strtoi(paste0(S,"0",S))
# "37" 2 37037
## Numeri romani
as.roman(1944)
# MCMXLIV
## Rapporti < 1 in basi varie (4/100 in base 2, 55 cifre)
MNB(4,100, 2,55)
# 0. 0 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0
# 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 resto 36
Esempi - 29 (vedi)
F <- function(x) x*(x-2); G <- function(x) x/2
graficoF(F,-1,3, "blue"); grafico(G,-1,3, "red")
# vedi i grafici sotto a sinistra
diseq(F,G,-1,3,"black")
diseq(F,G,-1,3,"black")
diseq(G,F,-1,3,"orange")
diseq(G,F,-1,3,"orange")

 # Per il grafico a destra ( |x^2-3*x-3| < |x^2+5*x-8| ) vedi qui.
k <- function(x,y) abs(x)+abs(y)-1
PIANO(-2,2, -2,2); curva(k,"blue"); diseq1(k,0,"red")
#
h <- function(x,y) (x-1)^2+0.5*(y+3)^2
# dove h < 2 e dove h > 3
PIANO(-3,3, -6,0)
diseq1(h,2, "blue"); diseq1(h,2, "blue")
diseq2(h,3, "red"); diseq2(h,3, "red")
#
P <- function(x,y) x >= y & x-y <=1 & 0 <= x & x <= 1
# dove P è vera (val. 1) e dove è falsa (val. 0)
PIANO(-2,2, -2,2)
diseq1(P,1,"blue"); diseq1(P,1,"blue") # falsa
diseq2(P,0, "red"); diseq2(P,0, "red") # vera
for(i in 1:10) diseq1(P,1,"blue"); for(i in 1:10) diseq2(P,0,"red")
# Per il grafico a destra ( |x^2-3*x-3| < |x^2+5*x-8| ) vedi qui.
k <- function(x,y) abs(x)+abs(y)-1
PIANO(-2,2, -2,2); curva(k,"blue"); diseq1(k,0,"red")
#
h <- function(x,y) (x-1)^2+0.5*(y+3)^2
# dove h < 2 e dove h > 3
PIANO(-3,3, -6,0)
diseq1(h,2, "blue"); diseq1(h,2, "blue")
diseq2(h,3, "red"); diseq2(h,3, "red")
#
P <- function(x,y) x >= y & x-y <=1 & 0 <= x & x <= 1
# dove P è vera (val. 1) e dove è falsa (val. 0)
PIANO(-2,2, -2,2)
diseq1(P,1,"blue"); diseq1(P,1,"blue") # falsa
diseq2(P,0, "red"); diseq2(P,0, "red") # vera
for(i in 1:10) diseq1(P,1,"blue"); for(i in 1:10) diseq2(P,0,"red")
 # Attenzione: il software non basta
# Vediamo la risoluzione di 3/(4*x – 5) > 4.
Piano(-5,5, -5,5)
f <- function(x) 3/(4*x-5); g <- function(x) 4
grafico(f,-5,5, 1); grafico(g,-5,5, "red")
# Capisco che le soluzioni sono in un intervallino tra 0 e 2, ma
# per rappresentare la diseq. devo avere un intervallo in cui i due
# grafici non abbiano salti. Dove è il salto? Risolvo l'equazione
# 4*x-5 = 0. È facile, ma vediamo come farlo col computer:
h <- function(x) 4*x-5; soluz(h,0, 0,2)
# 1.25
Piano(0,2,-1,8); grafico(f,0,2, 1); grafico(g,0,2, "red")
diseq(g,f, 1.25,2, "brown"); diseq(g,f, 1.25,2, "brown")
# Attenzione: il software non basta
# Vediamo la risoluzione di 3/(4*x – 5) > 4.
Piano(-5,5, -5,5)
f <- function(x) 3/(4*x-5); g <- function(x) 4
grafico(f,-5,5, 1); grafico(g,-5,5, "red")
# Capisco che le soluzioni sono in un intervallino tra 0 e 2, ma
# per rappresentare la diseq. devo avere un intervallo in cui i due
# grafici non abbiano salti. Dove è il salto? Risolvo l'equazione
# 4*x-5 = 0. È facile, ma vediamo come farlo col computer:
h <- function(x) 4*x-5; soluz(h,0, 0,2)
# 1.25
Piano(0,2,-1,8); grafico(f,0,2, 1); grafico(g,0,2, "red")
diseq(g,f, 1.25,2, "brown"); diseq(g,f, 1.25,2, "brown")
 # Ho una conferma grafica: la punteggiatura mostra che la soluzione è l'intervallo
# (1.25,q). Per trovare q tengo conto che le curve si incontrano tra 1.25 e 1.5:
soluz2(f,g, 1.25,1.5)
# 1.4375
# Per avere l'intervallo in forma frazionaria:
frazio(1.25); frazio(1.4375)
# 5/4 23/16
puntino(5/4,0,"blue"); puntino(23/16,0,"red")
Esempi - 30 (vedi)
# Devo usare u,v,w come parametri e du,dv,dw come passi
# Cliccando puoi variare i parametri.
# In grigio viene tracciata la curva precedente.
# Cliccando il bottone blu vedi il grafico più spesso.
# I grafici polari sono in scala monometrica.
# Una parabola in (-5,5)×(-10,10) al variare dei coefficienti
h <- function(x) u*x^2+v*x+w
u <- 1; du <- 0.5; v <- 1; dv <- 1; w <- 0; dw <- 0.5
BF=5; HF=4 # se vuoi aumenta le dimensioni
fun3p(h,-5,5, -10,10)
# Ho una conferma grafica: la punteggiatura mostra che la soluzione è l'intervallo
# (1.25,q). Per trovare q tengo conto che le curve si incontrano tra 1.25 e 1.5:
soluz2(f,g, 1.25,1.5)
# 1.4375
# Per avere l'intervallo in forma frazionaria:
frazio(1.25); frazio(1.4375)
# 5/4 23/16
puntino(5/4,0,"blue"); puntino(23/16,0,"red")
Esempi - 30 (vedi)
# Devo usare u,v,w come parametri e du,dv,dw come passi
# Cliccando puoi variare i parametri.
# In grigio viene tracciata la curva precedente.
# Cliccando il bottone blu vedi il grafico più spesso.
# I grafici polari sono in scala monometrica.
# Una parabola in (-5,5)×(-10,10) al variare dei coefficienti
h <- function(x) u*x^2+v*x+w
u <- 1; du <- 0.5; v <- 1; dv <- 1; w <- 0; dw <- 0.5
BF=5; HF=4 # se vuoi aumenta le dimensioni
fun3p(h,-5,5, -10,10)





 Esempi - 31 (vedi)
# Che cosa posso dire della funzione lineare F tale che F(5) = 10
# il cui grafico passa per i punti dotati di precisione
# x: 12±1 17±1 24±1 33±1.5
# y: 18±2 27±2 31±2.5 45±3
Piano(0,35, 0,50)
x <- c(12, 17, 24, 33); ex <- c(1, 1, 1, 1.5)
y <- c(18, 27, 31, 45); ey <- c(2, 2, 2.5, 3)
puntiapp(5,10, x,y, ex,ey)
# 1.153846 * x + 4.230769 1.153846 * (x - 5 ) + 10
# 1.305556 * x + 3.472222 1.305556 * (x - 5 ) + 10
# Ottengo la figura sottostante a destra:
Esempi - 31 (vedi)
# Che cosa posso dire della funzione lineare F tale che F(5) = 10
# il cui grafico passa per i punti dotati di precisione
# x: 12±1 17±1 24±1 33±1.5
# y: 18±2 27±2 31±2.5 45±3
Piano(0,35, 0,50)
x <- c(12, 17, 24, 33); ex <- c(1, 1, 1, 1.5)
y <- c(18, 27, 31, 45); ey <- c(2, 2, 2.5, 3)
puntiapp(5,10, x,y, ex,ey)
# 1.153846 * x + 4.230769 1.153846 * (x - 5 ) + 10
# 1.305556 * x + 3.472222 1.305556 * (x - 5 ) + 10
# Ottengo la figura sottostante a destra:
 # Se volessi esprimere i valori in forma frazionaria:
puntiapp2(5,10, x,y, ex,ey)
# 15/13 55/13 15/13 5 10 47/36 125/36 47/36 5 10
# deduco: 15/13*x+55/13 15/13*(x-5)+10 47/36*x+125/36 47/36*(x-5)+10
# Se volessi esprimere i valori in forma frazionaria:
puntiapp2(5,10, x,y, ex,ey)
# 15/13 55/13 15/13 5 10 47/36 125/36 47/36 5 10
# deduco: 15/13*x+55/13 15/13*(x-5)+10 47/36*x+125/36 47/36*(x-5)+10
 # Per trovare le intersezioni considero:
h = function(x) g(x, f(x)); graficoF( h, -5,5, "blue")
# ottengo il grafico sopra a destra, in cui vedo meglio le "x" soluzioni
soluz(h,0, 0,2)
# 1.153846
piu(soluz(h,0, 0,2))
# 1.15384615384615
frazio(soluz(h,0, 0,2))
# 15/13
soluz(h,0, 2,4)
# 3
# Le x sono 15/13 e 3, trovo le y
f(15/13); f(3)
# 5.769231 3
frazio( f(15/13) )
# 75/13
# Le soluzioni sono (x,y) = (15/13, 75/13) e (x,y) = (3,3), che posso controllare sul
# grafico sopra a sinistra.
Esempi - 33 (vedi)
f <- function(x) cos(x)
pend(f, -3.2,0, -1.6,1.6, -pi/2)
# Per trovare le intersezioni considero:
h = function(x) g(x, f(x)); graficoF( h, -5,5, "blue")
# ottengo il grafico sopra a destra, in cui vedo meglio le "x" soluzioni
soluz(h,0, 0,2)
# 1.153846
piu(soluz(h,0, 0,2))
# 1.15384615384615
frazio(soluz(h,0, 0,2))
# 15/13
soluz(h,0, 2,4)
# 3
# Le x sono 15/13 e 3, trovo le y
f(15/13); f(3)
# 5.769231 3
frazio( f(15/13) )
# 75/13
# Le soluzioni sono (x,y) = (15/13, 75/13) e (x,y) = (3,3), che posso controllare sul
# grafico sopra a sinistra.
Esempi - 33 (vedi)
f <- function(x) cos(x)
pend(f, -3.2,0, -1.6,1.6, -pi/2)
 Esempi - 34 (vedi)
# prodotto scalare e (solo nel caso tridimensionale) prodotto vettoriale
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# la somma di vettori si fa col "+" (se li rappresento con freccia, non con Freccia,
# in cui - come abbiamo visto - metto i vettori come dir. e modulo):
v1 <- c(2,3); v2 <- c(-4,1)
PIANO(-4,2, -1,5)
freccia(0,0,v1[1],v1[2], "red")
freccia(0,0,v2[1],v2[2], "blue")
freccia(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
frec(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
frec(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# ricordo che mettere come colore 1 equivale a mettere "black"
Esempi - 34 (vedi)
# prodotto scalare e (solo nel caso tridimensionale) prodotto vettoriale
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# la somma di vettori si fa col "+" (se li rappresento con freccia, non con Freccia,
# in cui - come abbiamo visto - metto i vettori come dir. e modulo):
v1 <- c(2,3); v2 <- c(-4,1)
PIANO(-4,2, -1,5)
freccia(0,0,v1[1],v1[2], "red")
freccia(0,0,v2[1],v2[2], "blue")
freccia(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
frec(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
frec(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# ricordo che mettere come colore 1 equivale a mettere "black"
 # la direzione e la lunghezza della freccia rossa:
dirFreccia(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# il suo versore e, con un altro comando, la sua lunghezza:
versore(v1); modulo(v1)
# 0.5547002 0.8320503 3.605551
# areaF; esempi per N = 2, 4, 10 mila, 100 mila per una certa f
BF=3; HF=2
f <- function(x) sqrt(1-x^2)
PIANO(-1,1, 0,1); areaF(f,-1,1,2) # 1
PIANO(-1,1, 0,1); areaF(f,-1,1,4) # 1.3660254
PIANO(-1,1, 0,1); areaF(f,-1,1,1e4) # 1.5707947
PIANO(-1,1, 0,1); areaF(f,-1,1,1e5) # 1.5707963 (=π/2)
# la direzione e la lunghezza della freccia rossa:
dirFreccia(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# il suo versore e, con un altro comando, la sua lunghezza:
versore(v1); modulo(v1)
# 0.5547002 0.8320503 3.605551
# areaF; esempi per N = 2, 4, 10 mila, 100 mila per una certa f
BF=3; HF=2
f <- function(x) sqrt(1-x^2)
PIANO(-1,1, 0,1); areaF(f,-1,1,2) # 1
PIANO(-1,1, 0,1); areaF(f,-1,1,4) # 1.3660254
PIANO(-1,1, 0,1); areaF(f,-1,1,1e4) # 1.5707947
PIANO(-1,1, 0,1); areaF(f,-1,1,1e5) # 1.5707963 (=π/2)
 # Usa areaF2 se (per N grande) vuoi un calcolo più veloce
# altro esempio (grafici sotto a sinistra):
Piano(0,3,0,3); areaF(floor, 0,3, 2) # 3.75
Piano(0,3,0,3); areaF(floor, 0,3, 1000) # 3.0015
# Usa areaF2 se (per N grande) vuoi un calcolo più veloce
# altro esempio (grafici sotto a sinistra):
Piano(0,3,0,3); areaF(floor, 0,3, 2) # 3.75
Piano(0,3,0,3); areaF(floor, 0,3, 1000) # 3.0015

 # Le aree sono orientate: positive/negative se stanno sopra/sotto l'asse x
# (figure sopra a destra)
f1 <- function(x) -x^2+1; f2 <- function(x) -f1(x)
BF=3; HF=3
PIANO(-1,1, -1,1); areaF(f1,-1,1,2000) # 1.333333
PIANO(-1,1, -1,1); areaF(f2,-1,1,2000) # -1.333333
# Calcolando opportuni integrali (vedi sotto) posso calcolare facilmente
# le aree di molte figure
#
# Vediamo come calcolare l'integrale di una funzione definita per punti:
# Le aree sono orientate: positive/negative se stanno sopra/sotto l'asse x
# (figure sopra a destra)
f1 <- function(x) -x^2+1; f2 <- function(x) -f1(x)
BF=3; HF=3
PIANO(-1,1, -1,1); areaF(f1,-1,1,2000) # 1.333333
PIANO(-1,1, -1,1); areaF(f2,-1,1,2000) # -1.333333
# Calcolando opportuni integrali (vedi sotto) posso calcolare facilmente
# le aree di molte figure
#
# Vediamo come calcolare l'integrale di una funzione definita per punti:
 x = c(10,13, 17, 19); y = c(7,1,9,8)
Piano(min(x),max(x), 0,max(y)); spezza(x,y,"blue")
integr = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
integr(x,y) # 49
#
# lunghezza curve. Esempi (nei vari modi) per il calcolo della semicirconferenza
x = c(10,13, 17, 19); y = c(7,1,9,8)
Piano(min(x),max(x), 0,max(y)); spezza(x,y,"blue")
integr = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
integr(x,y) # 49
#
# lunghezza curve. Esempi (nei vari modi) per il calcolo della semicirconferenza


 # Vedi qui per un esempio di "studio di funzione"
# Vedi qui per un esempio di "studio di funzione"
 F = function(x,y,z) 5*x^2*y^3+x^3*z
derivata(F,"x"); derivata(F,"z")
# 5*(2*x)*y^3+3*x^2*z x^3
derivata2(F,"y"); derivata2(F,"z")
# 5*x^2*(3*(2*y)) 0
derivataxy(F,"x","y"); derivataxy(F,"x","z")
# 5*(2*x)*(3*y^2) 3*x^2
#
Q = function(x,y) x^4+6*x^2*y^2+y^4-32*(x^2+y^2)
# per calcolare l'hessiano le variabili devono essere x ed y
hessiano(Q,0,0), hessiano(Q,0,4); hessiano(Q,2,-2)
# 4096 16384 -8192
#
# integrali
g <- function(x) sin(x)
integrale(sin, 0,pi/2); integrale(sin, 0,pi); integrale(sin, 0,2*pi)
# 1 2 2.032977e-16 ("praticamente" 0)
Piano(-pi,2*pi, -1,1); grafic(cos, -pi,2*pi, "blue")
gintegra(cos, 0,2*pi, "red"); gintegra(cos, 0,-pi, "violet")
punto(0,0, "red")
F = function(x,y,z) 5*x^2*y^3+x^3*z
derivata(F,"x"); derivata(F,"z")
# 5*(2*x)*y^3+3*x^2*z x^3
derivata2(F,"y"); derivata2(F,"z")
# 5*x^2*(3*(2*y)) 0
derivataxy(F,"x","y"); derivataxy(F,"x","z")
# 5*(2*x)*(3*y^2) 3*x^2
#
Q = function(x,y) x^4+6*x^2*y^2+y^4-32*(x^2+y^2)
# per calcolare l'hessiano le variabili devono essere x ed y
hessiano(Q,0,0), hessiano(Q,0,4); hessiano(Q,2,-2)
# 4096 16384 -8192
#
# integrali
g <- function(x) sin(x)
integrale(sin, 0,pi/2); integrale(sin, 0,pi); integrale(sin, 0,2*pi)
# 1 2 2.032977e-16 ("praticamente" 0)
Piano(-pi,2*pi, -1,1); grafic(cos, -pi,2*pi, "blue")
gintegra(cos, 0,2*pi, "red"); gintegra(cos, 0,-pi, "violet")
punto(0,0, "red")
 # È facile integrare numericamente e graficamente funzioni non facili da studiare "a
# mano". Vedi qui per un esempio.
# Nota 1. Se l'integrale tra -Inf e Inf viene 0 controlla se è finito anche quello tra
# 0 e Inf: se non accade significa che l'integrale diverge (è venuto 0 solo per una
# semplificazione formale)
# Nota 2. Per integrare una funzione tra a e b se essa non è definita in un punto c
# compreso tra a e b fai la somma dell'integrale tra a e c e di quello tra c e b
#
# Vedi qui come calcolare aree usando gli integrali
# È facile integrare numericamente e graficamente funzioni non facili da studiare "a
# mano". Vedi qui per un esempio.
# Nota 1. Se l'integrale tra -Inf e Inf viene 0 controlla se è finito anche quello tra
# 0 e Inf: se non accade significa che l'integrale diverge (è venuto 0 solo per una
# semplificazione formale)
# Nota 2. Per integrare una funzione tra a e b se essa non è definita in un punto c
# compreso tra a e b fai la somma dell'integrale tra a e c e di quello tra c e b
#
# Vedi qui come calcolare aree usando gli integrali
 Esempi - 35 (vedi)
A <- c(1,4, 5,4, 5,0, 1,0, 1,4, 3,5, 5,4); xTab(A); yTab(A)
# 1 5 5 1 1 3 5
# 4 4 0 0 4 5 4
PIANO(0,6, 0,6); spezzata(xTab(A), yTab(A), "red")
PIANO(0,6, 0,6); spezzaC(xTab(A), yTab(A), "yellow")
Esempi - 35 (vedi)
A <- c(1,4, 5,4, 5,0, 1,0, 1,4, 3,5, 5,4); xTab(A); yTab(A)
# 1 5 5 1 1 3 5
# 4 4 0 0 4 5 4
PIANO(0,6, 0,6); spezzata(xTab(A), yTab(A), "red")
PIANO(0,6, 0,6); spezzaC(xTab(A), yTab(A), "yellow")
 # Posso caricare coordinate (separate da ",") presenti in un file esterno.
# Ad es. se copio le coordinate presenti nel file penisola e le incollo
# dopo avere battuto
# I <- c( e infine battendo ) in modo da ottenere:
# I <- c(
# 8,46,
# 7.87,45.9,
# ...
# 8,46
# )
# Ecco che cosa ho come esito con questi altri comandi:
X <- xTab(I); Y <- yTab(I)
Piano(min(X),max(X), min(Y),max(Y)); spezzata(X,Y, "blue")
C <- centroPol(X,Y); C; PUNTI(C[1],C[2],"red")
# 12.18996 43.48932
# per centroPol vedi 25
Piano(min(X),max(X), min(Y),max(Y)); spezzaC(X,Y, "green"); spezza(X,Y, "red")
PUNTI(C[1],C[2],"red")
# Posso caricare coordinate (separate da ",") presenti in un file esterno.
# Ad es. se copio le coordinate presenti nel file penisola e le incollo
# dopo avere battuto
# I <- c( e infine battendo ) in modo da ottenere:
# I <- c(
# 8,46,
# 7.87,45.9,
# ...
# 8,46
# )
# Ecco che cosa ho come esito con questi altri comandi:
X <- xTab(I); Y <- yTab(I)
Piano(min(X),max(X), min(Y),max(Y)); spezzata(X,Y, "blue")
C <- centroPol(X,Y); C; PUNTI(C[1],C[2],"red")
# 12.18996 43.48932
# per centroPol vedi 25
Piano(min(X),max(X), min(Y),max(Y)); spezzaC(X,Y, "green"); spezza(X,Y, "red")
PUNTI(C[1],C[2],"red")
 # Vedi qui per caricare dati come quelli di "penisola" salvati come tabella
#
# Un pipistrello:
boxmN(-6,6, -6,6) # con PIANO(-6,6, -6,6) avrei anche la griglia; con PIANOss(-6,6, -6,6)
# non avrei la griglia ma l'immagine riempirebbe meno la finestra
P <- c(
0, 1.05, 0.1,1.05, 0.35,1, 0.8,1.3, 0.6,0.95,
1.5,0.9, 5,4, 5.55,4, 6,3, 5,1,
1.45,-1.9, 1.8,-2.4, 1.6,-2.5, 1.35,-2, 0,-2.9,
-1.35,-2, -1.6,-2.5, -1.8,-2.4, -1.45,-1.9, -5,1,
-6,3, -5.55,4, -5,4, -1.5,0.9, -0.6,0.95,
-0.8,1.3, -0.35,1, -0.1,1.05, 0,1.05 )
X <- xTab(P); Y <- yTab(P)
spezzaC(X,Y,"grey"); spezzata(X,Y,"black")
# Vedi qui per caricare dati come quelli di "penisola" salvati come tabella
#
# Un pipistrello:
boxmN(-6,6, -6,6) # con PIANO(-6,6, -6,6) avrei anche la griglia; con PIANOss(-6,6, -6,6)
# non avrei la griglia ma l'immagine riempirebbe meno la finestra
P <- c(
0, 1.05, 0.1,1.05, 0.35,1, 0.8,1.3, 0.6,0.95,
1.5,0.9, 5,4, 5.55,4, 6,3, 5,1,
1.45,-1.9, 1.8,-2.4, 1.6,-2.5, 1.35,-2, 0,-2.9,
-1.35,-2, -1.6,-2.5, -1.8,-2.4, -1.45,-1.9, -5,1,
-6,3, -5.55,4, -5,4, -1.5,0.9, -0.6,0.95,
-0.8,1.3, -0.35,1, -0.1,1.05, 0,1.05 )
X <- xTab(P); Y <- yTab(P)
spezzaC(X,Y,"grey"); spezzata(X,Y,"black")
 Esempi - 36 (vedi)
x <- c(-0.2, 1.3, 1.7, 3.2, 4.1, 4.6)
y <- c(9.1, 17.5, 20.7, 25.4, 35.7, 51.2)
Piano(-1,6,-10,70); PUNTI(x,y,1)
regressione(x,y, 0,0); PUNTI(0,0,"blue")
# 9.829 * x
f <- function(x) 9.829 * x; grafico(f,-1,6, "red")
regressione1(x,y)
# 7.628 * x + 7.911
g <- function(x) 7.628 * x + 7.911; grafico(g,-1,6, "blue")
regressione2(x,y)
# 1.37 * x^2 + 1.38 * x + 11.2
h <- function(x) 1.37 * x^2 + 1.38 * x + 11.2; grafico(h,-1,6, "violet")
regressione3(x,y)
# 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6
k <- function(x) 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6; grafico(k,-1,6, "green")
PUNTI(0,0,"blue"); PUNTI(x,y,1)
Esempi - 36 (vedi)
x <- c(-0.2, 1.3, 1.7, 3.2, 4.1, 4.6)
y <- c(9.1, 17.5, 20.7, 25.4, 35.7, 51.2)
Piano(-1,6,-10,70); PUNTI(x,y,1)
regressione(x,y, 0,0); PUNTI(0,0,"blue")
# 9.829 * x
f <- function(x) 9.829 * x; grafico(f,-1,6, "red")
regressione1(x,y)
# 7.628 * x + 7.911
g <- function(x) 7.628 * x + 7.911; grafico(g,-1,6, "blue")
regressione2(x,y)
# 1.37 * x^2 + 1.38 * x + 11.2
h <- function(x) 1.37 * x^2 + 1.38 * x + 11.2; grafico(h,-1,6, "violet")
regressione3(x,y)
# 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6
k <- function(x) 1.21 * x^3 + -6.3 * x^2 + 11.9 * x + 11.6; grafico(k,-1,6, "green")
PUNTI(0,0,"blue"); PUNTI(x,y,1)

 # A destra è rappresenta invece la spline cubica che interpola i punti (vedi):
Piano(-1,6,-10,70); PUNTI(x,y,1); L=spline(x,y,1000)
# ho calcolato e messo in L le coordinate di 1000 punti della
# spline passante per i punti x,y
spezzata(L$x,L$y,"red") # l'ho tracciata in rosso
# Quella "prolungata" che passa per gli stessi punti abbassati di 10
PUNTI(x,y-10,1); L1=spline(x,y-10,1000, xmin=-1,xmax=5)
spezzata(L1$x,L1$y, "blue")
#
# La curva che passa esattamente per (-1,-10),(0,-1),(1,-2),(2,5)
PIANO(-2,3,-20,20)
punto(-1,-10, 1); punto(0,-1,"red"); punto(1,-2,"green"); punto(2,5,"blue")
regressione3( c(-1,0,1,2), c(-10,-1,-2,5) )
# 3 * x^3 + -5 * x^2 + 1 * x + -1
f <- function(x) 3 * x^3 + -5 * x^2 + 1 * x + -1
grafico(f,-2,3, 6)
# A destra è rappresenta invece la spline cubica che interpola i punti (vedi):
Piano(-1,6,-10,70); PUNTI(x,y,1); L=spline(x,y,1000)
# ho calcolato e messo in L le coordinate di 1000 punti della
# spline passante per i punti x,y
spezzata(L$x,L$y,"red") # l'ho tracciata in rosso
# Quella "prolungata" che passa per gli stessi punti abbassati di 10
PUNTI(x,y-10,1); L1=spline(x,y-10,1000, xmin=-1,xmax=5)
spezzata(L1$x,L1$y, "blue")
#
# La curva che passa esattamente per (-1,-10),(0,-1),(1,-2),(2,5)
PIANO(-2,3,-20,20)
punto(-1,-10, 1); punto(0,-1,"red"); punto(1,-2,"green"); punto(2,5,"blue")
regressione3( c(-1,0,1,2), c(-10,-1,-2,5) )
# 3 * x^3 + -5 * x^2 + 1 * x + -1
f <- function(x) 3 * x^3 + -5 * x^2 + 1 * x + -1
grafico(f,-2,3, 6)
 Esempi - 37 (vedi)
xx <- c(-1,-1,0,0,1,1)
yy <- c(0,1,1,-1,-1,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,0); bezier(xx,-yy,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,"red"); bezier(xx,-yy,"black")
Esempi - 37 (vedi)
xx <- c(-1,-1,0,0,1,1)
yy <- c(0,1,1,-1,-1,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,0); bezier(xx,-yy,0)
PIANO(-1,1,-1,1)
bezier(xx,yy,"red"); bezier(xx,-yy,"black")
 # altri esempi qui
Esempi - 38 (vedi)
x <- c(0,2,3,6); y <- c(1,2,4,5)
rigcol(2,3) # 2 righe e 3 colonne
Boxm_(0,6,0,6); Spezzata(x,y, "blue"); Boxm_(0,6,0,6); Spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzata(x,y, "blue"); Boxm_(0,6,0,6); spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzat(x,y, "blue"); Boxm_(0,6,0,6); PUNTI(x,y, "blue")
# Boxm_ apre una finestra nel riquadro monometrica, lasciando i margini
# altri esempi qui
Esempi - 38 (vedi)
x <- c(0,2,3,6); y <- c(1,2,4,5)
rigcol(2,3) # 2 righe e 3 colonne
Boxm_(0,6,0,6); Spezzata(x,y, "blue"); Boxm_(0,6,0,6); Spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzata(x,y, "blue"); Boxm_(0,6,0,6); spezza(x,y, "blue")
Boxm_(0,6,0,6); spezzat(x,y, "blue"); Boxm_(0,6,0,6); PUNTI(x,y, "blue")
# Boxm_ apre una finestra nel riquadro monometrica, lasciando i margini
 rigcol(2,3)
Box_(0,6,0,6); Spezzata(x,y, "blue"); Box_(0,6,0,6); Spezza(x,y, "blue")
Box_(0,6,0,6); spezzata(x,y, "blue"); Box_(0,6,0,6); spezza(x,y, "blue")
Box_(0,6,0,6); spezzat(x,y, "blue"); Box_(0,6,0,6); PUNTI(x,y, "blue")
# Box_ apre una finestra nel riquadro, lasciando i margini
rigcol(2,3)
Box_(0,6,0,6); Spezzata(x,y, "blue"); Box_(0,6,0,6); Spezza(x,y, "blue")
Box_(0,6,0,6); spezzata(x,y, "blue"); Box_(0,6,0,6); spezza(x,y, "blue")
Box_(0,6,0,6); spezzat(x,y, "blue"); Box_(0,6,0,6); PUNTI(x,y, "blue")
# Box_ apre una finestra nel riquadro, lasciando i margini
 rigcol(2,3)
BoxN(0,6,0,6); BOX(); Spezzata(x,y, "blue"); BoxN(0,6,0,6); Spezza(x,y, "blue")
BoxN(0,6,0,6); spezzata(x,y, "blue"); BoxN(0,6,0,6); spezza(x,y, "blue")
BoxN(0,6,0,6); BOX(); spezzat(x,y, "blue"); BoxN(0,6,0,6); PUNTI(x,y, "blue")
# BoxN già visto in 25 (non lascia margini)
rigcol(2,3)
BoxN(0,6,0,6); BOX(); Spezzata(x,y, "blue"); BoxN(0,6,0,6); Spezza(x,y, "blue")
BoxN(0,6,0,6); spezzata(x,y, "blue"); BoxN(0,6,0,6); spezza(x,y, "blue")
BoxN(0,6,0,6); BOX(); spezzat(x,y, "blue"); BoxN(0,6,0,6); PUNTI(x,y, "blue")
# BoxN già visto in 25 (non lascia margini)
 Esempi - 39 (vedi)
# Soluzione grafica di eq.diff. del 1° ord. col metodo di Eulero:
# soledif(x0,y0,xf,N,col) traccia la poligonale approssimante con N passi il graf. della
# sol. di y' = f(x,y) (quella passante per (x0,y0), da x0 a xf), con f messa in Dy
# Esempio: y'=x-y tale che (x0,y0)=(-1,3) per -1 <= x <= 5
Dy <- function(x,y) x-y
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "brown")
soledif(-1,3, 5, 1e3, "blue")
# Capisco che con N = 1000 il grafico si è stabilizzato. In genere N = 1e4
soledif(4,2.5, -1, 1e4, "red")
# è sufficiente; se il grafico ha molte oscillazioni occorre aumentare N
# Se voglio vedere il campo direzionale per 20 righe e 25 colonne faccio
diredif(-1,5, -2,5, 25,20)
# Se voglio vedere solo questo non metto le righe "soledif"
# Altri esempi per la stessa equazione (fig. a destra):
Piano(-1,5, -2,5)
soledif(1,0, 5, 1e4, "brown"); soledif(1,0, -1, 1e4, "blue")
soledif(2,1.5, 5, 1e4, "brown"); soledif(2,1.5, -1, 1e4, "blue")
soledif(3,1, 5, 1e4, "brown"); soledif(3,1, -1, 1e4, "blue")
Esempi - 39 (vedi)
# Soluzione grafica di eq.diff. del 1° ord. col metodo di Eulero:
# soledif(x0,y0,xf,N,col) traccia la poligonale approssimante con N passi il graf. della
# sol. di y' = f(x,y) (quella passante per (x0,y0), da x0 a xf), con f messa in Dy
# Esempio: y'=x-y tale che (x0,y0)=(-1,3) per -1 <= x <= 5
Dy <- function(x,y) x-y
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "brown")
soledif(-1,3, 5, 1e3, "blue")
# Capisco che con N = 1000 il grafico si è stabilizzato. In genere N = 1e4
soledif(4,2.5, -1, 1e4, "red")
# è sufficiente; se il grafico ha molte oscillazioni occorre aumentare N
# Se voglio vedere il campo direzionale per 20 righe e 25 colonne faccio
diredif(-1,5, -2,5, 25,20)
# Se voglio vedere solo questo non metto le righe "soledif"
# Altri esempi per la stessa equazione (fig. a destra):
Piano(-1,5, -2,5)
soledif(1,0, 5, 1e4, "brown"); soledif(1,0, -1, 1e4, "blue")
soledif(2,1.5, 5, 1e4, "brown"); soledif(2,1.5, -1, 1e4, "blue")
soledif(3,1, 5, 1e4, "brown"); soledif(3,1, -1, 1e4, "blue")
 # soledifp(x0,y0,xf,N,col) traccia solo gli N+1 punti senza congiungerli
Piano(-1,5, -2,5)
soledifp(-1,3, 5, 10, "black")
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "red")
soledifp(-1,3, 5, 10, "black")
# soledifp(x0,y0,xf,N,col) traccia solo gli N+1 punti senza congiungerli
Piano(-1,5, -2,5)
soledifp(-1,3, 5, 10, "black")
Piano(-1,5, -2,5)
soledif(-1,3, 5, 10, "red")
soledifp(-1,3, 5, 10, "black")
 Esempi - 40 (vedi)
casa()
( poi premi INVIO per far partire il programma )
# teta, fi e ind.dist indicano la posizione dell'occhio: la direzione
# dello sguardo proiettata sul piano orizzontale, la sua inclinazione
# rispetto a tale piano e la distanza dell'occhio dal centro del box.
Esempi - 40 (vedi)
casa()
( poi premi INVIO per far partire il programma )
# teta, fi e ind.dist indicano la posizione dell'occhio: la direzione
# dello sguardo proiettata sul piano orizzontale, la sua inclinazione
# rispetto a tale piano e la distanza dell'occhio dal centro del box.
 GRAF3DIM()
Se batti GRAF3D(10,5,1) vedi il grafico della funzione che dentro
al cerchio di centro (0,0) e raggio 1 vale sqrt(x^2+y^2) e al
di fuori vale 0, vista dalla direzione teta=10°, fi=5° e da una
particolare distanza. Con GRAF3D(10,5,3) allontani l'occhio.
Prova con GRAF3D(0,30,1/2) GRAF3D(10,30,2) GRAF3D(10,-30,2)
GRAF3DIM()
Se batti GRAF3D(10,5,1) vedi il grafico della funzione che dentro
al cerchio di centro (0,0) e raggio 1 vale sqrt(x^2+y^2) e al
di fuori vale 0, vista dalla direzione teta=10°, fi=5° e da una
particolare distanza. Con GRAF3D(10,5,3) allontani l'occhio.
Prova con GRAF3D(0,30,1/2) GRAF3D(10,30,2) GRAF3D(10,-30,2)
 BOH()
Se batti INCL(5,10) vedi una figura da una inclinazione di 5°, con
scala tale che le porzioni di assi x,y,z (colorati nero, verde e
rosso) siano lunghe 10. La stiamo guardando un po' a sinistra del
piano yz. La figura è una parabola. E' possibile? Prova con
INCL(10,10), INCL(15,10), INCL(40,10), INCL(40,200), INCL(40,2000)
INCL(5,10)
BOH()
Se batti INCL(5,10) vedi una figura da una inclinazione di 5°, con
scala tale che le porzioni di assi x,y,z (colorati nero, verde e
rosso) siano lunghe 10. La stiamo guardando un po' a sinistra del
piano yz. La figura è una parabola. E' possibile? Prova con
INCL(10,10), INCL(15,10), INCL(40,10), INCL(40,200), INCL(40,2000)
INCL(5,10)




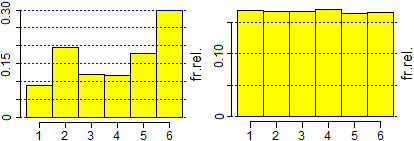
 Esempi - 42 (vedi)
# Batti ripetutamente escher() Otterrai successive tassellazioni casuali.
escher();
escher();
...
Vedi qui per approfondimenti.
Esempi - 42 (vedi)
# Batti ripetutamente escher() Otterrai successive tassellazioni casuali.
escher();
escher();
...
Vedi qui per approfondimenti.
 Esempi - 43 (vedi)
struttura(1*2+3) # la somma (+) del prodotto (*) di 1 per 2 e di 3
# `+`
# `*`
# [1] 1
# [1] 2
# [1] 3
struttura(1+2*3) # la "+" di 1 e del "*" di 2 per 3
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
struttura(1+2*3+4) # la "+" della ("+" di 1 e del "*" di 2 per 3) e di 4
# `+`
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
# [1] 4
struttura( 1*(2+3) ) # il "*" di 1 per la "+" di 2 e 3
# `*`
# [1] 1
# `(`
# `+`
# [1] 2
# [1] 3
# La parentesi "(" compare solo per specificare che il 2º termine di * non è un singolo
# termine [questo è il motivo per cui non compare ")"]
struttura( -sqrt(1+2)*3 ) # il "*" della "negaz" della ("√" della "+" di 1 e 2) per 3
# `*`
# `-`
# sqrt
# `+`
# [1] 1
# [1] 2
# [1] 3
struttura( -1-2*3^-4 ) # la "-" tra la "negaz" di 1 e il "*" di 2 per (3 alla "negaz" di 4)
# `-`
# `-`
# [1] 1
# `*`
# [1] 2
# `^`
# [1] 3
# `-`
# [1] 4
Esempi - 44 (vedi)
Per la realizzazione di grafi ad albero con opportuni comandi vedi qui.
Per realizzare grafi di flusso vedi qui.
Esempi - 43 (vedi)
struttura(1*2+3) # la somma (+) del prodotto (*) di 1 per 2 e di 3
# `+`
# `*`
# [1] 1
# [1] 2
# [1] 3
struttura(1+2*3) # la "+" di 1 e del "*" di 2 per 3
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
struttura(1+2*3+4) # la "+" della ("+" di 1 e del "*" di 2 per 3) e di 4
# `+`
# `+`
# [1] 1
# `*`
# [1] 2
# [1] 3
# [1] 4
struttura( 1*(2+3) ) # il "*" di 1 per la "+" di 2 e 3
# `*`
# [1] 1
# `(`
# `+`
# [1] 2
# [1] 3
# La parentesi "(" compare solo per specificare che il 2º termine di * non è un singolo
# termine [questo è il motivo per cui non compare ")"]
struttura( -sqrt(1+2)*3 ) # il "*" della "negaz" della ("√" della "+" di 1 e 2) per 3
# `*`
# `-`
# sqrt
# `+`
# [1] 1
# [1] 2
# [1] 3
struttura( -1-2*3^-4 ) # la "-" tra la "negaz" di 1 e il "*" di 2 per (3 alla "negaz" di 4)
# `-`
# `-`
# [1] 1
# `*`
# [1] 2
# `^`
# [1] 3
# `-`
# [1] 4
Esempi - 44 (vedi)
Per la realizzazione di grafi ad albero con opportuni comandi vedi qui.
Per realizzare grafi di flusso vedi qui.



 Esempi - 45 (vedi)
Vai qui
Esempi - 45 (vedi)
Vai qui



 # Controlliamo la struttura dell'ultimo grafo:
struttura( (1^2)*-3/(4-5)+6*7 )
# `+`
# `/`
# `*`
# `(`
# `^`
# [1] 1
# [1] 2
# `-`
# [1] 3
# `(`
# `-`
# [1] 4
# [1] 5
# `*`
# [1] 6
# [1] 7
# Un esercizio:
# dalle uscite relative a un termine incognito risalire ad esso e al grafo.
`+`
`/`
`*`
A
`-`
`(`
`+`
A
B
`(`
`-`
A
`(`
`+`
C
D
E
# Controlliamo la struttura dell'ultimo grafo:
struttura( (1^2)*-3/(4-5)+6*7 )
# `+`
# `/`
# `*`
# `(`
# `^`
# [1] 1
# [1] 2
# `-`
# [1] 3
# `(`
# `-`
# [1] 4
# [1] 5
# `*`
# [1] 6
# [1] 7
# Un esercizio:
# dalle uscite relative a un termine incognito risalire ad esso e al grafo.
`+`
`/`
`*`
A
`-`
`(`
`+`
A
B
`(`
`-`
A
`(`
`+`
C
D
E
 # Le due colonne di dati sono chiamate V1 e V2. Le metto in X e Y con:
X <- T$V1; Y <- T$V2 # Volendo guardo i dati con data.entry(X) e ...(Y)
# Procedo come sopra:
HF=4; BF=4
Piano(min(X),max(X), min(Y),max(Y)); spezza(X,Y, "blue")
C <- centroPol(X,Y); PUNTO(C[1],C[2], "black")
# Le due colonne di dati sono chiamate V1 e V2. Le metto in X e Y con:
X <- T$V1; Y <- T$V2 # Volendo guardo i dati con data.entry(X) e ...(Y)
# Procedo come sopra:
HF=4; BF=4
Piano(min(X),max(X), min(Y),max(Y)); spezza(X,Y, "blue")
C <- centroPol(X,Y); PUNTO(C[1],C[2], "black")
 #
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice
# (da 01 a 23 i comandi scritti in blu sono illustrati nel documento precedente):
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
abs sign rad2-rad5 factorial choose %/% ?Math gradi funz.circolari
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
prod
# 06 Rivedere i comandi (^ v). function
cancellare variabili messaggi d'errore str
# 07 Arrotondare numeri e risultati.
trunc print signif piu ultimo write cat tabulazioni
# 08 Le sequenze di numeri: seq :
ricorsione
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
operare su varie finestre grafiche
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
arco P()
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
l'indicazione dei colori con numeri
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
semir r2p a2p cartamm rect
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
poligono regolare poligo poligoC
spezzaL spezza2L text \n frec2 freccia2 Direzionex Direzioney
RotTraMol MolTraRot xpunta ypunta (il punto finale dell'ultimo segmento)
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
scriviC scriviR scriviRC
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
sottoassex suAssex sottoassex ...
# 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm1/…, TERMOMETRO
tortaC TortaC TortaM StrisciaC Torta2C … torta2 torta_C …
BarreC BARREC BARRE BARRE2
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
quantile(daticlas, …) boxAB hist
Approfondimenti (simulazioni)
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
curva cur graficF grafic grafiF grafi distPF (distanza punto-grafico)
# 23 Risolvere equazioni (soluz).
soluz2 equazioni polinomiali solpol sommap prodp
if for while { } connettivi
####
# 24 Calcolo approssimato.
# approssima approssima2 EPS
# 25 Animazioni e altro su Finestre e Punti. Centroide (baricentro)
# boxN BoxN boxmN BoxmN BOX() BOXs() BOXg() NF() PPP() puntiB puntiniB punticiniB
# palliniB puntiBm puntiniBm punticiniBm palliniBm Spezzata Spezza spezzat
# puntoO puntoV puntoD puntiO/V/D linea Linea LInea centroPol
# 26 Orologi e pause
# Ore Minuti Secondi Sec attendi orologio orologio2
# 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
# param polar para par1 pola pol1 rottramol rottra moltrarot ZZZ
# 28 Calcoli tra interi comunque grandi. Stringhe <-> Numeri Basi ≠ dieci
# som pro dif app strtoi nchar substr NUMERO paste0 as.roman MNB
# 29 Disequazioni
# diseq diseq1 diseq2
# 30 Curve al variare dei parametri
# fun3p polar3p curva4p
# 31 Punti dotati di precisione. Retta approssimante
# puntiapp
# 32 Risoluzione di sistemi lineari e di sistemi in due incognite
# sistema soluzione
# 33 Pendenza di un grafico
# pend
# 34 Calcolo vettor., differenz. e integrale, lunghezze ed aree
# (e num. complessi, matrici, funz. più var., limiti, serie)
# prodv prods modulo versore derivata integrale gintegrale gintegra
# lungFun lungPar lungPolar areaPar areaPolar derivataxy hessiano
# 35 Immagini date le coordinate
# xTab yTab
# 36 Regressione, spline
# regressione regressione1 regressione2 regressione3 spline
# 37 Curve di Bezier
# 38 Grafici multipli
# rigcol colrig
# 39 Equazioni differenziali
# soledif diredif
# 40 Prospettiva
# 41 Lancio di dadi
# 42 Escher
# 43 Struttura dei termini
# 44 Grafi ad albero
# 45 Altre immagini
#
#
# INDICE
# Guarda uscite e immagini per cercare ciò che ti serve. Comunque ecco qui un indice
# (da 01 a 23 i comandi scritti in blu sono illustrati nel documento precedente):
# 01 Che cosa caricare all'avvio. Come sono visualizzate le uscite.
# 02 Più comandi sulla stessa riga. Il punto decimale. *
# 03 Notazione esponenziale. ^ sqrt Grafi ad albero: Alberi()
abs sign rad2-rad5 factorial choose %/% ?Math gradi funz.circolari
# 04 Le variabili. <- = Le dimensioni delle lettere.
# 05 Le collezioni di numeri. [ ] sum
prod
# 06 Rivedere i comandi (^ v). function
cancellare variabili messaggi d'errore str
# 07 Arrotondare numeri e risultati.
trunc print signif piu ultimo write cat tabulazioni
# 08 Le sequenze di numeri: seq :
ricorsione
# 09 Frazioni. Ordinare numeri. Divisioni. Divisori. Numeri primi. MCD MCM
# 10 Il PIANO (monometrico).
# 11 Le dimensioni della finestra dei grafici (BF HF)
# 12 Spostare, ridimensionare, cancellare le finestre grafiche.
operare su varie finestre grafiche
# 13 punto punti Punti PUNTI cerchio cerchio3p centro3p raggio3p
arco P()
# 14 Il Piano non monometrico. xy(n): le coordinate del punto che clicco. I colori.
l'indicazione dei colori con numeri
# 15 segm semiretta retta2p medio2p asse2p Piano senza e con griglie
semir r2p a2p cartamm rect
# 16 spezzata lung inclinazione pendenza spezzaC areaPol freccia
Direzione Distanze punto_punto punto_retta Intersezione retta_retta
poligono regolare poligo poligoC
spezzaL spezza2L text \n frec2 freccia2 Direzionex Direzioney
RotTraMol MolTraRot xpunta ypunta (il punto finale dell'ultimo segmento)
# 17 Inserire scritte (scrivi). Misurare gli angoli (angolo).
Punti di un cerchio date le direzioni (cerchioA / A2 cerchio3pA / A2 xrot yrot)
Un triangolo dati i 3 lati o 2 lati e 1 angolo o 1 lato e 2 angoli
scriviC scriviR scriviRC
# 18 Come realizzare grafici per punti, come mettere scritte sugli assi
sottoassex suAssex sottoassex ...
# 19 Diagrammi a torta, barre, striscia. Goniometro. cartamm1/…, TERMOMETRO
tortaC TortaC TortaM StrisciaC Torta2C … torta2 torta_C …
BarreC BARREC BARRE BARRE2
# 20 istogramma max min length median mean Istogramma noClassi stem di dati
# rep altrestat (e boxplot) Andare a capo
quantile(daticlas, …) boxAB hist
Approfondimenti (simulazioni)
# 21 pi greca PERCENTUALI RAPPORTI
# 22 Grafici di funzioni a 1 input/1 output graficoF grafico NpuntiF maxmin tratteggi
curva cur graficF grafic grafiF grafi distPF (distanza punto-grafico)
# 23 Risolvere equazioni (soluz).
soluz2 equazioni polinomiali solpol sommap prodp
if for while { } connettivi
####
# 24 Calcolo approssimato.
# approssima approssima2 EPS
# 25 Animazioni e altro su Finestre e Punti. Centroide (baricentro)
# boxN BoxN boxmN BoxmN BOX() BOXs() BOXg() NF() PPP() puntiB puntiniB punticiniB
# palliniB puntiBm puntiniBm punticiniBm palliniBm Spezzata Spezza spezzat
# puntoO puntoV puntoD puntiO/V/D linea Linea LInea centroPol
# 26 Orologi e pause
# Ore Minuti Secondi Sec attendi orologio orologio2
# 27 Curve in forma parametrica/polare, rotaz./trasl./dilataz.
# param polar para par1 pola pol1 rottramol rottra moltrarot ZZZ
# 28 Calcoli tra interi comunque grandi. Stringhe <-> Numeri Basi ≠ dieci
# som pro dif app strtoi nchar substr NUMERO paste0 as.roman MNB
# 29 Disequazioni
# diseq diseq1 diseq2
# 30 Curve al variare dei parametri
# fun3p polar3p curva4p
# 31 Punti dotati di precisione. Retta approssimante
# puntiapp
# 32 Risoluzione di sistemi lineari e di sistemi in due incognite
# sistema soluzione
# 33 Pendenza di un grafico
# pend
# 34 Calcolo vettor., differenz. e integrale, lunghezze ed aree
# (e num. complessi, matrici, funz. più var., limiti, serie)
# prodv prods modulo versore derivata integrale gintegrale gintegra
# lungFun lungPar lungPolar areaPar areaPolar derivataxy hessiano
# 35 Immagini date le coordinate
# xTab yTab
# 36 Regressione, spline
# regressione regressione1 regressione2 regressione3 spline
# 37 Curve di Bezier
# 38 Grafici multipli
# rigcol colrig
# 39 Equazioni differenziali
# soledif diredif
# 40 Prospettiva
# 41 Lancio di dadi
# 42 Escher
# 43 Struttura dei termini
# 44 Grafi ad albero
# 45 Altre immagini