# Another example:
# Integral of (x,y) → x^3*y in T.
# I define F so:
F = function(x,y) ifelse(x^2+y^2<=1, x^3*y, 0)
# What is the range of F?
MAXF2(F, 0,1, 0,1)
# ~ max in x,y F(max) 0.8675266 0.4973907 0.3247477
MINF2(F, 0,1, 0,1)
# ~ min in x,y F(min) 0.7265506 0.7270941 0.0000000
# From 0 to 0.3; I expect an integral much lower than 1
INTEGRAL(F, 0,1, 0,1, 200)
# 0.04166803
INTEGRAL(F, 0,1, 0,1, 400)
# 0.04166006
INTEGRAL(F, 0,1, 0,1, 800)
# 0.0416674
INTEGRAL(F, 0,1, 0,1, 1600)
# 0.04166695
fraction(0.0416666666666)
# 1/24
# | 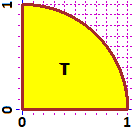 |
#
# Another example:
# integral of f in the triangle ->
f = function(x,y) exp((y-x)/(x+y))
PLANE(0,3, 0,3); g = function(x,y) x+y-2; CURVE(g, "brown")
# I define F so:
F = function(x,y) ifelse(y <= 2-x, f(x,y), 0)
# I put the found values in u: |  |


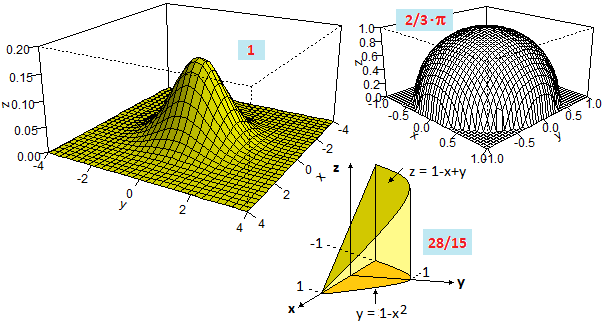 # [1] A bivariate gaussian (just a small N value is enough):
F = function(x,y) 1/(2*pi)*exp(-(x^2+y^2)/2)
u = INTEGRAL(F,-20,20, -20,20, 10); u
# 0.1865616
u = INTEGRAL(F,-20,20, -20,20, 20); u
# 0.9714394
u =INTEGRAL(F,-20,20, -20,20, 50); u
# 1
#
# [2] The half-sphere of radius 1 (I put 0 out of the domain):
g = function(x,y) ifelse(x^2+y^2>1, 0, sqrt(1-x^2-y^2) )
u = INTEGRAL(g,-1,1, -1,1, 500); u
# 2.094412
u = INTEGRAL(g,-1,1, -1,1, 1000); u
# 2.094397
u/pi
# 0.6666674
fraction(0.6666666666666)
# 2/3 The integral is 2/3·π
#
# [3] The function in the 3rd graph (I put 0 out of the domain):
F = function(x,y) ifelse(y > 1-x^2, 0, 1-x+y)
u = INTEGRAL(F,-1,1, 0,1, 250); more(u)
# 1.86677023999999
u = INTEGR(F,-1,1, 0,1, 500); more(u)
# 1.86705564800002
u = INTEGR(F,-1,1, 0,1, 1000); more(u)
# 1.86669718
fraction(1.866666666666666)
# 28/15
# Using WolframAlpha:
# integrate(integrate 1-x+y, y =0..1-x^2), x = -1..1
# 28/15
#
# I N is very large, approximation errors can become preponderant.
#
# Another example: integral of (x,y) -> x*y^2 in the following figure
# between y=x^2 and x=y^2
# [1] A bivariate gaussian (just a small N value is enough):
F = function(x,y) 1/(2*pi)*exp(-(x^2+y^2)/2)
u = INTEGRAL(F,-20,20, -20,20, 10); u
# 0.1865616
u = INTEGRAL(F,-20,20, -20,20, 20); u
# 0.9714394
u =INTEGRAL(F,-20,20, -20,20, 50); u
# 1
#
# [2] The half-sphere of radius 1 (I put 0 out of the domain):
g = function(x,y) ifelse(x^2+y^2>1, 0, sqrt(1-x^2-y^2) )
u = INTEGRAL(g,-1,1, -1,1, 500); u
# 2.094412
u = INTEGRAL(g,-1,1, -1,1, 1000); u
# 2.094397
u/pi
# 0.6666674
fraction(0.6666666666666)
# 2/3 The integral is 2/3·π
#
# [3] The function in the 3rd graph (I put 0 out of the domain):
F = function(x,y) ifelse(y > 1-x^2, 0, 1-x+y)
u = INTEGRAL(F,-1,1, 0,1, 250); more(u)
# 1.86677023999999
u = INTEGR(F,-1,1, 0,1, 500); more(u)
# 1.86705564800002
u = INTEGR(F,-1,1, 0,1, 1000); more(u)
# 1.86669718
fraction(1.866666666666666)
# 28/15
# Using WolframAlpha:
# integrate(integrate 1-x+y, y =0..1-x^2), x = -1..1
# 28/15
#
# I N is very large, approximation errors can become preponderant.
#
# Another example: integral of (x,y) -> x*y^2 in the following figure
# between y=x^2 and x=y^2



