#
# Vediamo come fare qualche altra analisi statistica di dati.
#
# Ecco un modo alternativo a quelli visti in g.htm e g_1.htm per costruire un
# diagramma a torta ("pie" in inglese). Vediamo come rappresentare
# le estensioni complessive delle zone di collina, montagna e pianura
# del Piemonte espresse in decine di chilometri quadrati:
# primo modo (semplicissimo):
pie(c(770,1099,671))
# modo più sofisticato (aggiungo i nomi):
piemonte <- c(770,1099,671)
names(piemonte) <- c("col","mon","pia")
pie(piemonte)
# scelgo anche i colori:
pie(piemonte,col=c("yellow","brown","green"))
 #
# Se voglio mantenere il precedente diagramma posso fare il successivo
# in una nuova finestra, che posso aprire col comando dev.new()
#
# La rappresentazione con un diagramma a barre ("barplot"), primo modo:
barplot(piemonte)
# Eccola riducendo lo spazio tra le colonne e mettendo una griglia
barplot(piemonte,space=0)
# Traccia linee orizzontali a certe quote, tratteggiate
abline(h=c(200,400,600,800,1000),lty=3)
# Eccola aggiungendo colori:
barplot(piemonte,space=0,col=c("yellow","brown","green"))
abline(h=c(200,400,600,800,1000),lty=3)
#
# Se voglio mantenere il precedente diagramma posso fare il successivo
# in una nuova finestra, che posso aprire col comando dev.new()
#
# La rappresentazione con un diagramma a barre ("barplot"), primo modo:
barplot(piemonte)
# Eccola riducendo lo spazio tra le colonne e mettendo una griglia
barplot(piemonte,space=0)
# Traccia linee orizzontali a certe quote, tratteggiate
abline(h=c(200,400,600,800,1000),lty=3)
# Eccola aggiungendo colori:
barplot(piemonte,space=0,col=c("yellow","brown","green"))
abline(h=c(200,400,600,800,1000),lty=3)
 # La distribuzione percentuale (sum fa la somma):
piemonte/sum(piemonte)*100
col mon pia
30.31496 43.26772 26.41732
# Il suo arrotondamento agli interi
round(piemonte/sum(piemonte)*100)
col mon pia
30 43 26
# e ai decimi
round(piemonte/sum(piemonte)*100, 1)
col mon pia
30.3 43.3 26.4
# Ecco il diagramma con le percentuali:
colori <- c("yellow","brown","green")
barplot(piemonte/sum(piemonte)*100,space=0,col=colori)
abline(h=c(10,20,30,40),lty=3)
# La distribuzione percentuale (sum fa la somma):
piemonte/sum(piemonte)*100
col mon pia
30.31496 43.26772 26.41732
# Il suo arrotondamento agli interi
round(piemonte/sum(piemonte)*100)
col mon pia
30 43 26
# e ai decimi
round(piemonte/sum(piemonte)*100, 1)
col mon pia
30.3 43.3 26.4
# Ecco il diagramma con le percentuali:
colori <- c("yellow","brown","green")
barplot(piemonte/sum(piemonte)*100,space=0,col=colori)
abline(h=c(10,20,30,40),lty=3)
 #
#
# Ecco le altezze di 3 ragazze di scuola media e l'esito di alcuni calcoli:
x <- c(145,152,147)
c( min(x), max(x), sum(x) )
[1] 145 152 444
c( length(x), sum(x)/length(x), mean(x) )
[1] 3 148 148
# si sono trovati il minimo, il massimo e la somma dei dati; poi si sono
# scritti quanti sono i dati (la "lunghezza" di x), la loro media, espressa
# come somma divisa per il numero dei dati o direttamente.
#
# Vediamo la analoga analisi fatta su più dati:
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
c( min(alu), max(alu), length(alu) )
[1] 140 161 18
# Mettiamo i dati in ordine ("sort" in inglese significa "sorta", "specie" ma
# anche "ordinamento")
sort(alu)
[1] 140 145 146 147 147 149 150 152 152 153 153 154 155 155 156 157 158 161
c( min(alu), max(alu), length(alu), mean(alu), median(alu) )
[1] 140.0000 161.0000 18.0000 151.6667 152.5000
# Si noti che quando si stampano più dati usando c(...) essi vengono tutti
# scritti con cifre dopo il "." se ce n'è qualcuno che ne ha.
# Alla fine abbiamo stampato anche il valore della mediana ossia il valore
# che sta al centro dell'elenco.
#
# Ecco l'istogramma. Il programma sceglie automaticamente le classi in cui
# classificare i dati. Il comando è hist.
hist(alu, right=FALSE)
# L'espressione "right=FALSE" serve per comunicare al programma che vogliamo che gli
# intervalli siano del tipo […,…), in modo che ad esempio 150 non sia classificato
# tra 145 e 150 ma tra 150 e 155: 150 non sta in [145,150) ma sta in [150,155).
#
#
# Ecco le altezze di 3 ragazze di scuola media e l'esito di alcuni calcoli:
x <- c(145,152,147)
c( min(x), max(x), sum(x) )
[1] 145 152 444
c( length(x), sum(x)/length(x), mean(x) )
[1] 3 148 148
# si sono trovati il minimo, il massimo e la somma dei dati; poi si sono
# scritti quanti sono i dati (la "lunghezza" di x), la loro media, espressa
# come somma divisa per il numero dei dati o direttamente.
#
# Vediamo la analoga analisi fatta su più dati:
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
c( min(alu), max(alu), length(alu) )
[1] 140 161 18
# Mettiamo i dati in ordine ("sort" in inglese significa "sorta", "specie" ma
# anche "ordinamento")
sort(alu)
[1] 140 145 146 147 147 149 150 152 152 153 153 154 155 155 156 157 158 161
c( min(alu), max(alu), length(alu), mean(alu), median(alu) )
[1] 140.0000 161.0000 18.0000 151.6667 152.5000
# Si noti che quando si stampano più dati usando c(...) essi vengono tutti
# scritti con cifre dopo il "." se ce n'è qualcuno che ne ha.
# Alla fine abbiamo stampato anche il valore della mediana ossia il valore
# che sta al centro dell'elenco.
#
# Ecco l'istogramma. Il programma sceglie automaticamente le classi in cui
# classificare i dati. Il comando è hist.
hist(alu, right=FALSE)
# L'espressione "right=FALSE" serve per comunicare al programma che vogliamo che gli
# intervalli siano del tipo […,…), in modo che ad esempio 150 non sia classificato
# tra 145 e 150 ma tra 150 e 155: 150 non sta in [145,150) ma sta in [150,155).
 # Vengono rappresentate le frequenze delle varie classi in cui sono stati
# suddivisi i dati. Se aggiungiamo probability=TRUE otteniamo la stessa figura
# (vedi immagine di sopra, a destra), ma cambia la scala verticale: sono
# rappresentate non le frequenze ma le frequenze relative unitarie (o densità di
# frequenza), ossia le frequenze relative divise per l'ampiezza degli intervalli.
hist(alu, right=FALSE, probability=TRUE, col="yellow"); abline(h=0.06,lty=3)
# Tra 150 e 155 c'erano 6 dati; i dati sono 18, quindi la frequenza relativa è
# 6/18 = 0.333… (cioè 33.333…%), e quella unitaria è 6/18/5 = 0.06666… = 6.7%.
#
# Come faccio a trovare frequenze assolute e quelle percentuali (ossia le
# frequenze relative in forma percentuale) facilmente? Ecco:
hist(alu,right=FALSE)$counts
[1] 1 5 6 5 1
hist(alu,right=FALSE)$counts/length(alu)*100
[1] 5.555556 27.777778 33.333333 27.777778 5.555556
#
#
# Volendo posso decidere una sequenza di classi in cui classificare i dati.
# Basta che usi seq(A,B,h) per classificarli tra A e B in classi ampie h.
# Utilizziamo i dati alu già impiegati in precedenza.
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
hist(alu, right=FALSE, seq(140,161,3))
# Vengono rappresentate le frequenze delle varie classi in cui sono stati
# suddivisi i dati. Se aggiungiamo probability=TRUE otteniamo la stessa figura
# (vedi immagine di sopra, a destra), ma cambia la scala verticale: sono
# rappresentate non le frequenze ma le frequenze relative unitarie (o densità di
# frequenza), ossia le frequenze relative divise per l'ampiezza degli intervalli.
hist(alu, right=FALSE, probability=TRUE, col="yellow"); abline(h=0.06,lty=3)
# Tra 150 e 155 c'erano 6 dati; i dati sono 18, quindi la frequenza relativa è
# 6/18 = 0.333… (cioè 33.333…%), e quella unitaria è 6/18/5 = 0.06666… = 6.7%.
#
# Come faccio a trovare frequenze assolute e quelle percentuali (ossia le
# frequenze relative in forma percentuale) facilmente? Ecco:
hist(alu,right=FALSE)$counts
[1] 1 5 6 5 1
hist(alu,right=FALSE)$counts/length(alu)*100
[1] 5.555556 27.777778 33.333333 27.777778 5.555556
#
#
# Volendo posso decidere una sequenza di classi in cui classificare i dati.
# Basta che usi seq(A,B,h) per classificarli tra A e B in classi ampie h.
# Utilizziamo i dati alu già impiegati in precedenza.
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
hist(alu, right=FALSE, seq(140,161,3))
 # Per scritte sugli assi più piccole potrei mettere hist(…, cex.axis=0.88)
#
# Con summary ho una sintesi delle informazioni numeriche sui dati.
# Vengono stampati anche il 1° e il 3° quartile, cioè i dati che stanno
# a metà della prima metà e a metà della seconda metà dei dati; la
# mediana sarebbe il 2° quartile.
summary(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
# Volendo, se hai caricato il file seguente:
# source("http://macosa.dima.unige.it/r.R")
# hai gli stessi esiti e una loro rappresentazione grafica con:
statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
# Per scritte sugli assi più piccole potrei mettere hist(…, cex.axis=0.88)
#
# Con summary ho una sintesi delle informazioni numeriche sui dati.
# Vengono stampati anche il 1° e il 3° quartile, cioè i dati che stanno
# a metà della prima metà e a metà della seconda metà dei dati; la
# mediana sarebbe il 2° quartile.
summary(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
# Volendo, se hai caricato il file seguente:
# source("http://macosa.dima.unige.it/r.R")
# hai gli stessi esiti e una loro rappresentazione grafica con:
statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
 # in cui il "box" azzuro rappresenta i dati dal 1° al 3° quartile e i
# pallini rappresentano i valori che corrispondono a dove starebbero il
# 5º e il 95º dato se i dati, distribuiti in modo simile, fossero 100.
#
# Se abbiamo più dati da analizzare li mettiamo su più righe:
alu2 <- c(146,158,152,140,157,147,161,147,149,154,155,153,
155,156,150,153,152,145,158,140,147,149,155,156,153,145,
141,156,158,151,161,148,157,159,160,162,149,163,152,149,
157,155)
# Ecco la loro analisi statistica:
hist(alu2,right=FALSE)
hist(alu2,right=FALSE,seq(140,164,3))
# in cui il "box" azzuro rappresenta i dati dal 1° al 3° quartile e i
# pallini rappresentano i valori che corrispondono a dove starebbero il
# 5º e il 95º dato se i dati, distribuiti in modo simile, fossero 100.
#
# Se abbiamo più dati da analizzare li mettiamo su più righe:
alu2 <- c(146,158,152,140,157,147,161,147,149,154,155,153,
155,156,150,153,152,145,158,140,147,149,155,156,153,145,
141,156,158,151,161,148,157,159,160,162,149,163,152,149,
157,155)
# Ecco la loro analisi statistica:
hist(alu2,right=FALSE)
hist(alu2,right=FALSE,seq(140,164,3))
 summary(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
# Posso anche usare come sopra statistiche() fissando la stessa scala per alu e alu2,
# col comando boxAB:
BF=4;HF=1.2
boxAB=c(140,163); statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
boxAB=c(140,163); statistiche(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
I pallini sono il 5° e il 95° percentile
summary(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
# Posso anche usare come sopra statistiche() fissando la stessa scala per alu e alu2,
# col comando boxAB:
BF=4;HF=1.2
boxAB=c(140,163); statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
boxAB=c(140,163); statistiche(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
I pallini sono il 5° e il 95° percentile
 #
# Ecco come possiamo confrontare graficamente i due insiemi di dati:
hist(alu,seq(140,164,3),angle=45,density=7,probability=TRUE)
hist(alu2,seq(140,164,3),probability=TRUE,add=TRUE,angle=135,density=10)
# Ho aggiunto add=TRUE al comando per tracciare il 2° istogramma.
#
# Ecco come possiamo confrontare graficamente i due insiemi di dati:
hist(alu,seq(140,164,3),angle=45,density=7,probability=TRUE)
hist(alu2,seq(140,164,3),probability=TRUE,add=TRUE,angle=135,density=10)
# Ho aggiunto add=TRUE al comando per tracciare il 2° istogramma.

 # La rappresentazione a destra è stata ottenuta con questi comandi.
#
# Volendo posso introdurre una quantità variabile di input direttamente
# da tastiera mediante il comando scan(file="",n=...) in cui al posto
# di ... occorre mettere i dati da leggere. Due esempi. Il primo (faccio
# la somma di 3 numeri):
numeri <- scan(file="", n=3); sum(numeri)
1: 3
2: 7
3: 5
Read 3 items
[1] 15
# Il secondo (introduco un numero N e, poi, una quantità N di dati, di
# cui viene calcolata la media):
nalu <- scan(file="",n=1); altalu <- scan(file="",n=nalu); mean(altalu)
1: 7
Read 1 item
1: 154
2: 156
3: 163
4: 170
5: 161
6: 156
7: 159
Read 7 items
[1] 159.8571
#
#
# Un altro esempio di come i comandi possono essere spezzati su più
# righe. Ecco le lunghezze di molte fave (ossia semi di fava) raccolte
# da una classe di alunni di 12 anni. Occorre copiare e incollare tutte
# le righe, da "fave <- c(" alla riga finale ")".
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
# e il loro istogramma
hist(fave,right=FALSE)
# La rappresentazione a destra è stata ottenuta con questi comandi.
#
# Volendo posso introdurre una quantità variabile di input direttamente
# da tastiera mediante il comando scan(file="",n=...) in cui al posto
# di ... occorre mettere i dati da leggere. Due esempi. Il primo (faccio
# la somma di 3 numeri):
numeri <- scan(file="", n=3); sum(numeri)
1: 3
2: 7
3: 5
Read 3 items
[1] 15
# Il secondo (introduco un numero N e, poi, una quantità N di dati, di
# cui viene calcolata la media):
nalu <- scan(file="",n=1); altalu <- scan(file="",n=nalu); mean(altalu)
1: 7
Read 1 item
1: 154
2: 156
3: 163
4: 170
5: 161
6: 156
7: 159
Read 7 items
[1] 159.8571
#
#
# Un altro esempio di come i comandi possono essere spezzati su più
# righe. Ecco le lunghezze di molte fave (ossia semi di fava) raccolte
# da una classe di alunni di 12 anni. Occorre copiare e incollare tutte
# le righe, da "fave <- c(" alla riga finale ")".
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
# e il loro istogramma
hist(fave,right=FALSE)
 # e quello delle frequenze relative, con aggiunte delle righe
# tratteggiate orizzontali:
hist(fave,right=FALSE,probability=TRUE)
abline(h=c(1/2, 1, 1.5, 2, 2.5), lty=3)
# e quello delle frequenze relative, con aggiunte delle righe
# tratteggiate orizzontali:
hist(fave,right=FALSE,probability=TRUE)
abline(h=c(1/2, 1, 1.5, 2, 2.5), lty=3)
 # (il 2.5% dei dati sta tra 1.6 e 1.7 e un altro 2.5% tra 1.7 e 1.8)
# La sintesi delle informazioni:
summary(fave)
# ovvero, caricato: source("http://macosa.dima.unige.it/r.R")
statistiche(fave)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 1.550 1.650 1.659 1.750 2.300
# (il 2.5% dei dati sta tra 1.6 e 1.7 e un altro 2.5% tra 1.7 e 1.8)
# La sintesi delle informazioni:
summary(fave)
# ovvero, caricato: source("http://macosa.dima.unige.it/r.R")
statistiche(fave)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 1.550 1.650 1.659 1.750 2.300
 #
# Volendo posso scegliere io gli estremi degli intervalli. Se non li scelgo
# di uguale ampiezza viene tracciato l'istogramma con le frequenze relative.
hist(fave,c(1,1.3,1.5,1.7,1.9,2.3))
#
# Volendo posso scegliere io gli estremi degli intervalli. Se non li scelgo
# di uguale ampiezza viene tracciato l'istogramma con le frequenze relative.
hist(fave,c(1,1.3,1.5,1.7,1.9,2.3))
 #
# I dati possono essere copiati da rete e incollati in R o possono essere
# caricati da rete. Un esempio (il file"t-sec.txt" nella cartella "R").
# Leggo alcune righe (ad es. 4) di un file (ne leggo poche in quanto il file può
# essere lunghissimo, ad es. contenere qualche migliaia di dati):
readLines("http://macosa.dima.unige.it/R/t-sec.txt",n=4)
#[1] "# misure (troncate ai centesimi di sec) della durata di 1 s cronometrata a mano"
#[2] "111"
#[3] "103"
#[4] "109"
# Vedo che sono singoli dati interi e che c'è 1 riga da saltare. Lo faccio col
# comando skip. I dati sono separati da "aCapo"; li leggo col comando "scan"
# (se fossero separati da, ad es., ";" aggiungerei sep=";" )
dati <- scan("http://macosa.dima.unige.it/R/t-sec.txt", skip=1)
# Read 47 items
# In alternativa, posso esaminare il file da un browser (programma per navigare
# in Internet), copiarlo e poi usare scan("clipboard", skip=1)
# Il comando str visualizza la struttura di oggetti. Lo uso per esaminare dati
str(dati)
# num [1:47] 111 103 109 97 99 110 99 103 109 106 ...
# sono 47 dati. I dati sono troncati agli interi. Per fare valutazioni corrette
# devo avere dati arrotondati: aggiungo 1/2
DATI <- dati+1/2
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.86 108.00 129.50
hist(DATI,right=FALSE,seq(65,135,10))
# visto il grafico, scelgo la scala verticale in modo da vedere la quota 25
hist(DATI,right=FALSE,seq(65,135,10),ylim=c(0,25))
abline(h=c(5,10,15,20,25), lty=3)
#
# I dati possono essere copiati da rete e incollati in R o possono essere
# caricati da rete. Un esempio (il file"t-sec.txt" nella cartella "R").
# Leggo alcune righe (ad es. 4) di un file (ne leggo poche in quanto il file può
# essere lunghissimo, ad es. contenere qualche migliaia di dati):
readLines("http://macosa.dima.unige.it/R/t-sec.txt",n=4)
#[1] "# misure (troncate ai centesimi di sec) della durata di 1 s cronometrata a mano"
#[2] "111"
#[3] "103"
#[4] "109"
# Vedo che sono singoli dati interi e che c'è 1 riga da saltare. Lo faccio col
# comando skip. I dati sono separati da "aCapo"; li leggo col comando "scan"
# (se fossero separati da, ad es., ";" aggiungerei sep=";" )
dati <- scan("http://macosa.dima.unige.it/R/t-sec.txt", skip=1)
# Read 47 items
# In alternativa, posso esaminare il file da un browser (programma per navigare
# in Internet), copiarlo e poi usare scan("clipboard", skip=1)
# Il comando str visualizza la struttura di oggetti. Lo uso per esaminare dati
str(dati)
# num [1:47] 111 103 109 97 99 110 99 103 109 106 ...
# sono 47 dati. I dati sono troncati agli interi. Per fare valutazioni corrette
# devo avere dati arrotondati: aggiungo 1/2
DATI <- dati+1/2
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.86 108.00 129.50
hist(DATI,right=FALSE,seq(65,135,10))
# visto il grafico, scelgo la scala verticale in modo da vedere la quota 25
hist(DATI,right=FALSE,seq(65,135,10),ylim=c(0,25))
abline(h=c(5,10,15,20,25), lty=3)
 #
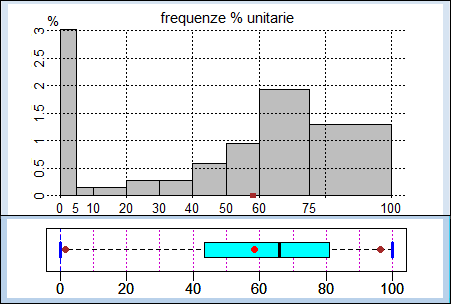
# Un'ultima osservazione.
# Se dispongo di dati già classificati, in intervalli di diversa ampiezza,
# posso riccorrere al comando istoclas presente nel file richiamabile con:
source("http://macosa.dima.unige.it/r.R")
# Vedi qui per un esempio:
#
# Un'ultima osservazione.
# Se dispongo di dati già classificati, in intervalli di diversa ampiezza,
# posso riccorrere al comando istoclas presente nel file richiamabile con:
source("http://macosa.dima.unige.it/r.R")
# Vedi qui per un esempio:
 #
# Possiamo generare dei numeri a caso. Ad es.
runif(4, min=1, max=10)
# [posso ottenere 9.139260 3.747637 3.847650 2.825768]
# genera 4 numeri casuali distribuiti "uniformemente" nell'intervallo (1,10).
# Invece:
trunc(runif(10, min=1, max=7))
# [ottengo ad esempio 2 4 1 4 5 3 4 6 2 5; "trunc" tronca un numero agli interi]
# genera 10 numeri casuali interi compresi tra 1 e 6
# Vediamo il lancio, 10 mila volte, di due dadi "equi":
n <- 10000; dadi <- trunc(runif(n, min=1, max=7))+trunc(runif(n, min=1, max=7))
# I valori sono stati messi in "dadi". Eccone alcuni:
dadi[1]; dadi[1:10]
# [1] 7
# [1] 7 9 9 7 8 6 4 10 7 7
hist(dadi, seq(1.5,12.5,1),probability=TRUE,col="yellow")
abline(h=c(0.05,0.1,0.15), lty=3)
#
# Possiamo generare dei numeri a caso. Ad es.
runif(4, min=1, max=10)
# [posso ottenere 9.139260 3.747637 3.847650 2.825768]
# genera 4 numeri casuali distribuiti "uniformemente" nell'intervallo (1,10).
# Invece:
trunc(runif(10, min=1, max=7))
# [ottengo ad esempio 2 4 1 4 5 3 4 6 2 5; "trunc" tronca un numero agli interi]
# genera 10 numeri casuali interi compresi tra 1 e 6
# Vediamo il lancio, 10 mila volte, di due dadi "equi":
n <- 10000; dadi <- trunc(runif(n, min=1, max=7))+trunc(runif(n, min=1, max=7))
# I valori sono stati messi in "dadi". Eccone alcuni:
dadi[1]; dadi[1:10]
# [1] 7
# [1] 7 9 9 7 8 6 4 10 7 7
hist(dadi, seq(1.5,12.5,1),probability=TRUE,col="yellow")
abline(h=c(0.05,0.1,0.15), lty=3)
 # Le uscite possibili sono 6*6 = 36; avendo supposto il dado "equo" sono tutte
# equiprobabili, ossia con probabilità 1/36. Ad es. 3 può uscire in 2 casi:
# 1 e 2, 2 ed 1; quindi la probabilità che esca è 2*1/36, ossia 0.0555…; e con
# 10 mila lanci ho ottenuto una frequenza relativa è vicina a 0.0555…
# L'istogramma a destra è stato ottenuto col comando Istogramma:
noClassi=1; Istogramma(dadi, 1.5,12.5, 1)
# Frequenze e frequenze percentuali:
#277, 554, 857, 1084, 1442, 1663, 1337, 1126, 862, 532, 266
#2.77,5.54,8.57,10.84,14.42,16.63,13.37,11.26,8.62,5.32,2.66
# La freq. relativa di 3 è 5.54% (ossia 0.0554).
#
# Posso trovare anche probabilità relative a fenomeni non facilmente studiabili in
# modo teorico. Vediamo come studiare le uscite del lancio di una coppia di dadi
# equi, assumendo come uscita la differenza dei valori che escono, che può
# andare da 0 a 5. Ci aspettiamo che 5 sia l'uscita meno probabile (viene solo se
# escono un 6 ed un 1), ma non è facile valutare gli altri casi.
# Per fare la differenza posso prendere il valore assoluto della sottrazione della
# seconda uscita dalla prima.
n=1e7; dadi=abs(trunc(runif(n, min=1,max=7))-trunc(runif(n, min=1,max=7)))
Istogramma(dadi,-0.5,5.5,1)
Frequenze e frequenze percentuali:
1666379, 2778367, 2221573, 1665591, 1111816, 556274
16.66,27.78,22.22,16.66,11.12,5.56
# Le uscite possibili sono 6*6 = 36; avendo supposto il dado "equo" sono tutte
# equiprobabili, ossia con probabilità 1/36. Ad es. 3 può uscire in 2 casi:
# 1 e 2, 2 ed 1; quindi la probabilità che esca è 2*1/36, ossia 0.0555…; e con
# 10 mila lanci ho ottenuto una frequenza relativa è vicina a 0.0555…
# L'istogramma a destra è stato ottenuto col comando Istogramma:
noClassi=1; Istogramma(dadi, 1.5,12.5, 1)
# Frequenze e frequenze percentuali:
#277, 554, 857, 1084, 1442, 1663, 1337, 1126, 862, 532, 266
#2.77,5.54,8.57,10.84,14.42,16.63,13.37,11.26,8.62,5.32,2.66
# La freq. relativa di 3 è 5.54% (ossia 0.0554).
#
# Posso trovare anche probabilità relative a fenomeni non facilmente studiabili in
# modo teorico. Vediamo come studiare le uscite del lancio di una coppia di dadi
# equi, assumendo come uscita la differenza dei valori che escono, che può
# andare da 0 a 5. Ci aspettiamo che 5 sia l'uscita meno probabile (viene solo se
# escono un 6 ed un 1), ma non è facile valutare gli altri casi.
# Per fare la differenza posso prendere il valore assoluto della sottrazione della
# seconda uscita dalla prima.
n=1e7; dadi=abs(trunc(runif(n, min=1,max=7))-trunc(runif(n, min=1,max=7)))
Istogramma(dadi,-0.5,5.5,1)
Frequenze e frequenze percentuali:
1666379, 2778367, 2221573, 1665591, 1111816, 556274
16.66,27.78,22.22,16.66,11.12,5.56
 # Per n = 10^7 (così come per n = 10^6) ottengo che l'uscita più frequente è 1
# (27.78% di probabilità).
# A questo punto posso provare a studiare il problema anche teoricamente ...
#
# Questo era un esempio di simulazione. Per valutare la precisione della stima si
# può ricorrere al seguente comando:
Pr <- function(n) {f <- 0; for (i in 1:n) f <- f + ifelse(Evento(),1,0);
fr <- f/n; S <- sqrt(fr*(1-fr)/(n-1)); cat(fr, "+/-", 3*S,'\n') }
# Introdotte queste righe e messo in Evento() una rappresentazione di un fenomeno
# di cui si vuole valutare la probabilità che valga 1 se esso si verifica e 0
# altrimenti, valutiamo, riferendoci all'esempio precedente, la probabilità che
# lanciando una coppia di dadi equi la loro differenza sia 1.
Evento <- function() abs(floor(runif(1)*6)-floor(runif(1)*6)) == 1
Pr(1e4)
#0.2825 +/- 0.01350713
Pr(1e5)
#0.27771 +/- 0.004248885
Pr(1e6)
#0.277448 +/- 0.001343219
Pr(1e7)
#0.2777537 +/- 0.000424907
# Possiamo dedurre che la probabilità è 0.2825±0.0135, anzi … 0.2777537±0.000425,
# ovvero 0.27775±0.00043. Andando avanti (se ho tempo …) posso trovare valutazioni
# più precise (queste valutazioni non sono certe, ma sono probabili al 99.7%).
# Una valutazione più complessa:
# qual è la probabilità, pescando 10 carte da un mazzo da 40, di ottenere almeno un
# tris (cioè 3 o 4 carte dello stesso valore)?
Evento <- function() {
ca <- array(rep(0,40),dim=c(4,10)); nu <- array(rep(0,10),dim=10)
tris <- 0; for (i in 1:10)
{ripeti <- 1; while(ripeti==1)
{seme <- floor(runif(1)*4)+1; valore <- floor(runif(1)*10)+1;
if (ca[seme,valore]==0) ripeti <- 0 }
ca[seme,valore] <- 1; nu[valore] <- nu[valore]+1;
for(valore in 1:10)
if (nu[valore]==3 | nu[valore]==4) {tris <- 1; valore <- 10}
};
ifelse(tris==1,1,0) }
# Descritto l'evento, valutiamo la probabilità:
Pr(1e3)
#0.409 +/- 0.04666528
Pr(1e4)
#0.3765 +/- 0.01453596
Pr(1e5)
#0.38396 +/- 0.004613929
Pr(1e6) # Per questa uscita occorre aspettare qualche minuto
#0.384978 +/- 0.001459771
# La probabilità cercata è 0.3850±0.0015, ovvero (38.50±0.15)%.
#
# Volendo generare P uscite casuali intere diverse tra loro che cadono tra M,M+1,...,N
# (N = P-1) uso sample(M:N). Esempi
sample(14:20)
#14 16 20 15 17 19 18
# La cosa è utile in molte situazioni. Es.: un generico ordine in cui posso estrarre
# le tredici carte di cuori:
sample(1:13)
#4 9 12 3 13 7 10 11 5 6 2 1 8
# Posso estrarre (del tutto a caso) 4 numeri tra 1 e 13:
sample(1:13, 4)
#6 10 11 12
#
# I numeri generati con runif e sample appaiono distribuiti in modo del tutto casuale.
# In realtà posso ottenere la stessa sequenza di numeri se batto set.seed(n) ("poni
# il seme eguale a n") con il medesimo numero intero n. Esempio:
sample(5:10); set.seed(273); sample(5:10); set.seed(273); sample(5:10)
# 6 10 7 5 8 9
# 6 7 5 9 10 8
# 6 7 5 9 10 8
set.seed(273); sample(5:10,3)
# 6 7 5
# La cosa è ad es. utile per controllare dei procedimenti che si vogliono realizzare
# in cui si impiega il generatore di numeri casuali.
# Per approfondimenti su come "è fatto" il generatore di numeri casuali vedi qui.
#
# Con questi comandi sono stati realizzati anche Codifica(seme,testo) e Decodifica(…,…)
# per realizzare codifiche "segrete"; occorre mettere in "seme" un numero intero.
# Ecco qualche esempio (vedi qui se vuoi vedere come sono stati realizzati):
frase = "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
Codifica(314, frase)
# "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/"
Decodifica(314, "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/")
# "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
frase2 = "195/3 = 65"
Codifica(-10, frase2)
# "F!I74TXTSI"
Decodifica(-10, "F!I74TXTSI")
# "195/3 = 65"
#
#
# NOTA tecnica su come "salvare" i grafici e i comandi usati.
# Per memorizzare un'immagine posso cliccare su di essa e dal menu che si
# apre salvarla come BitMap e poi o
# -- incollarla direttamente in un documento del programma con cui si sta
# scrivendo (OpenOffice, LibreOffice, Wordpad, Word, ...) o
# -- incollarla in Paint (o un altro programma di grafica), aggiungere
# quello che si vuole, spostarla e ridurre i margini, e poi o
# - copiarla nell'eventuale documento in cui si sta scrivendo o,
# - da Paint, salvarla in formato PNG o GIF, che occupano poco spazio.
# Per memorizzare i comandi usati posso, dal menu File, azionare il comando
# Save History che consente di salvare in un file (in formato testo) tutti
# i comandi eseguiti (devo dare un nome al file; posso lasciargli la
# estensione "Rhistory" o mettere l'estensione "txt"). Poi, dopo, posso
# [ o caricare automaticamente i comandi dal file usando il comando Load
# History, che può essere usato anche per richiamare automaticamente
# comandi caricati in altri file, o ]
# aprire il file con BloccoNote (NotePad) o un altro editor e copiare e
# incollare in R la sequenza di comandi che voglio.
#
# Per un formulario completo di tutti i comandi vai qui.
#
# Per usi più avanzati (scarto quadratico medio, gaussiana, altre distribuzioni,
# tabelle di contingenza, …) vai qui. Ricordiamo solo che accanto ai comandi presenti
# nel software var(dati) e sd(dati), che calcolano varianza e deviazione standard (o
# scarto quadratico medio) "sperimentali", sono presenti, se hai caricato:
# source("http://macosa.dima.unige.it/r.R")
# i comandi Var(dati), Sd(dati) e SdM(dati) che calcolano la varianza, la deviazione
# standard (o scarto quadratico medio) "teorici" e la deviazione standard della media.
#
# Per n = 10^7 (così come per n = 10^6) ottengo che l'uscita più frequente è 1
# (27.78% di probabilità).
# A questo punto posso provare a studiare il problema anche teoricamente ...
#
# Questo era un esempio di simulazione. Per valutare la precisione della stima si
# può ricorrere al seguente comando:
Pr <- function(n) {f <- 0; for (i in 1:n) f <- f + ifelse(Evento(),1,0);
fr <- f/n; S <- sqrt(fr*(1-fr)/(n-1)); cat(fr, "+/-", 3*S,'\n') }
# Introdotte queste righe e messo in Evento() una rappresentazione di un fenomeno
# di cui si vuole valutare la probabilità che valga 1 se esso si verifica e 0
# altrimenti, valutiamo, riferendoci all'esempio precedente, la probabilità che
# lanciando una coppia di dadi equi la loro differenza sia 1.
Evento <- function() abs(floor(runif(1)*6)-floor(runif(1)*6)) == 1
Pr(1e4)
#0.2825 +/- 0.01350713
Pr(1e5)
#0.27771 +/- 0.004248885
Pr(1e6)
#0.277448 +/- 0.001343219
Pr(1e7)
#0.2777537 +/- 0.000424907
# Possiamo dedurre che la probabilità è 0.2825±0.0135, anzi … 0.2777537±0.000425,
# ovvero 0.27775±0.00043. Andando avanti (se ho tempo …) posso trovare valutazioni
# più precise (queste valutazioni non sono certe, ma sono probabili al 99.7%).
# Una valutazione più complessa:
# qual è la probabilità, pescando 10 carte da un mazzo da 40, di ottenere almeno un
# tris (cioè 3 o 4 carte dello stesso valore)?
Evento <- function() {
ca <- array(rep(0,40),dim=c(4,10)); nu <- array(rep(0,10),dim=10)
tris <- 0; for (i in 1:10)
{ripeti <- 1; while(ripeti==1)
{seme <- floor(runif(1)*4)+1; valore <- floor(runif(1)*10)+1;
if (ca[seme,valore]==0) ripeti <- 0 }
ca[seme,valore] <- 1; nu[valore] <- nu[valore]+1;
for(valore in 1:10)
if (nu[valore]==3 | nu[valore]==4) {tris <- 1; valore <- 10}
};
ifelse(tris==1,1,0) }
# Descritto l'evento, valutiamo la probabilità:
Pr(1e3)
#0.409 +/- 0.04666528
Pr(1e4)
#0.3765 +/- 0.01453596
Pr(1e5)
#0.38396 +/- 0.004613929
Pr(1e6) # Per questa uscita occorre aspettare qualche minuto
#0.384978 +/- 0.001459771
# La probabilità cercata è 0.3850±0.0015, ovvero (38.50±0.15)%.
#
# Volendo generare P uscite casuali intere diverse tra loro che cadono tra M,M+1,...,N
# (N = P-1) uso sample(M:N). Esempi
sample(14:20)
#14 16 20 15 17 19 18
# La cosa è utile in molte situazioni. Es.: un generico ordine in cui posso estrarre
# le tredici carte di cuori:
sample(1:13)
#4 9 12 3 13 7 10 11 5 6 2 1 8
# Posso estrarre (del tutto a caso) 4 numeri tra 1 e 13:
sample(1:13, 4)
#6 10 11 12
#
# I numeri generati con runif e sample appaiono distribuiti in modo del tutto casuale.
# In realtà posso ottenere la stessa sequenza di numeri se batto set.seed(n) ("poni
# il seme eguale a n") con il medesimo numero intero n. Esempio:
sample(5:10); set.seed(273); sample(5:10); set.seed(273); sample(5:10)
# 6 10 7 5 8 9
# 6 7 5 9 10 8
# 6 7 5 9 10 8
set.seed(273); sample(5:10,3)
# 6 7 5
# La cosa è ad es. utile per controllare dei procedimenti che si vogliono realizzare
# in cui si impiega il generatore di numeri casuali.
# Per approfondimenti su come "è fatto" il generatore di numeri casuali vedi qui.
#
# Con questi comandi sono stati realizzati anche Codifica(seme,testo) e Decodifica(…,…)
# per realizzare codifiche "segrete"; occorre mettere in "seme" un numero intero.
# Ecco qualche esempio (vedi qui se vuoi vedere come sono stati realizzati):
frase = "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
Codifica(314, frase)
# "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/"
Decodifica(314, "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/")
# "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
frase2 = "195/3 = 65"
Codifica(-10, frase2)
# "F!I74TXTSI"
Decodifica(-10, "F!I74TXTSI")
# "195/3 = 65"
#
#
# NOTA tecnica su come "salvare" i grafici e i comandi usati.
# Per memorizzare un'immagine posso cliccare su di essa e dal menu che si
# apre salvarla come BitMap e poi o
# -- incollarla direttamente in un documento del programma con cui si sta
# scrivendo (OpenOffice, LibreOffice, Wordpad, Word, ...) o
# -- incollarla in Paint (o un altro programma di grafica), aggiungere
# quello che si vuole, spostarla e ridurre i margini, e poi o
# - copiarla nell'eventuale documento in cui si sta scrivendo o,
# - da Paint, salvarla in formato PNG o GIF, che occupano poco spazio.
# Per memorizzare i comandi usati posso, dal menu File, azionare il comando
# Save History che consente di salvare in un file (in formato testo) tutti
# i comandi eseguiti (devo dare un nome al file; posso lasciargli la
# estensione "Rhistory" o mettere l'estensione "txt"). Poi, dopo, posso
# [ o caricare automaticamente i comandi dal file usando il comando Load
# History, che può essere usato anche per richiamare automaticamente
# comandi caricati in altri file, o ]
# aprire il file con BloccoNote (NotePad) o un altro editor e copiare e
# incollare in R la sequenza di comandi che voglio.
#
# Per un formulario completo di tutti i comandi vai qui.
#
# Per usi più avanzati (scarto quadratico medio, gaussiana, altre distribuzioni,
# tabelle di contingenza, …) vai qui. Ricordiamo solo che accanto ai comandi presenti
# nel software var(dati) e sd(dati), che calcolano varianza e deviazione standard (o
# scarto quadratico medio) "sperimentali", sono presenti, se hai caricato:
# source("http://macosa.dima.unige.it/r.R")
# i comandi Var(dati), Sd(dati) e SdM(dati) che calcolano la varianza, la deviazione
# standard (o scarto quadratico medio) "teorici" e la deviazione standard della media.
#
 #
# Se voglio mantenere il precedente diagramma posso fare il successivo
# in una nuova finestra, che posso aprire col comando dev.new()
#
# La rappresentazione con un diagramma a barre ("barplot"), primo modo:
barplot(piemonte)
# Eccola riducendo lo spazio tra le colonne e mettendo una griglia
barplot(piemonte,space=0)
# Traccia linee orizzontali a certe quote, tratteggiate
abline(h=c(200,400,600,800,1000),lty=3)
# Eccola aggiungendo colori:
barplot(piemonte,space=0,col=c("yellow","brown","green"))
abline(h=c(200,400,600,800,1000),lty=3)
#
# Se voglio mantenere il precedente diagramma posso fare il successivo
# in una nuova finestra, che posso aprire col comando dev.new()
#
# La rappresentazione con un diagramma a barre ("barplot"), primo modo:
barplot(piemonte)
# Eccola riducendo lo spazio tra le colonne e mettendo una griglia
barplot(piemonte,space=0)
# Traccia linee orizzontali a certe quote, tratteggiate
abline(h=c(200,400,600,800,1000),lty=3)
# Eccola aggiungendo colori:
barplot(piemonte,space=0,col=c("yellow","brown","green"))
abline(h=c(200,400,600,800,1000),lty=3)
 # La distribuzione percentuale (sum fa la somma):
piemonte/sum(piemonte)*100
col mon pia
30.31496 43.26772 26.41732
# Il suo arrotondamento agli interi
round(piemonte/sum(piemonte)*100)
col mon pia
30 43 26
# e ai decimi
round(piemonte/sum(piemonte)*100, 1)
col mon pia
30.3 43.3 26.4
# Ecco il diagramma con le percentuali:
colori <- c("yellow","brown","green")
barplot(piemonte/sum(piemonte)*100,space=0,col=colori)
abline(h=c(10,20,30,40),lty=3)
# La distribuzione percentuale (sum fa la somma):
piemonte/sum(piemonte)*100
col mon pia
30.31496 43.26772 26.41732
# Il suo arrotondamento agli interi
round(piemonte/sum(piemonte)*100)
col mon pia
30 43 26
# e ai decimi
round(piemonte/sum(piemonte)*100, 1)
col mon pia
30.3 43.3 26.4
# Ecco il diagramma con le percentuali:
colori <- c("yellow","brown","green")
barplot(piemonte/sum(piemonte)*100,space=0,col=colori)
abline(h=c(10,20,30,40),lty=3)
 #
#
# Ecco le altezze di 3 ragazze di scuola media e l'esito di alcuni calcoli:
x <- c(145,152,147)
c( min(x), max(x), sum(x) )
[1] 145 152 444
c( length(x), sum(x)/length(x), mean(x) )
[1] 3 148 148
# si sono trovati il minimo, il massimo e la somma dei dati; poi si sono
# scritti quanti sono i dati (la "lunghezza" di x), la loro media, espressa
# come somma divisa per il numero dei dati o direttamente.
#
# Vediamo la analoga analisi fatta su più dati:
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
c( min(alu), max(alu), length(alu) )
[1] 140 161 18
# Mettiamo i dati in ordine ("sort" in inglese significa "sorta", "specie" ma
# anche "ordinamento")
sort(alu)
[1] 140 145 146 147 147 149 150 152 152 153 153 154 155 155 156 157 158 161
c( min(alu), max(alu), length(alu), mean(alu), median(alu) )
[1] 140.0000 161.0000 18.0000 151.6667 152.5000
# Si noti che quando si stampano più dati usando c(...) essi vengono tutti
# scritti con cifre dopo il "." se ce n'è qualcuno che ne ha.
# Alla fine abbiamo stampato anche il valore della mediana ossia il valore
# che sta al centro dell'elenco.
#
# Ecco l'istogramma. Il programma sceglie automaticamente le classi in cui
# classificare i dati. Il comando è hist.
hist(alu, right=FALSE)
# L'espressione "right=FALSE" serve per comunicare al programma che vogliamo che gli
# intervalli siano del tipo […,…), in modo che ad esempio 150 non sia classificato
# tra 145 e 150 ma tra 150 e 155: 150 non sta in [145,150) ma sta in [150,155).
#
#
# Ecco le altezze di 3 ragazze di scuola media e l'esito di alcuni calcoli:
x <- c(145,152,147)
c( min(x), max(x), sum(x) )
[1] 145 152 444
c( length(x), sum(x)/length(x), mean(x) )
[1] 3 148 148
# si sono trovati il minimo, il massimo e la somma dei dati; poi si sono
# scritti quanti sono i dati (la "lunghezza" di x), la loro media, espressa
# come somma divisa per il numero dei dati o direttamente.
#
# Vediamo la analoga analisi fatta su più dati:
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
c( min(alu), max(alu), length(alu) )
[1] 140 161 18
# Mettiamo i dati in ordine ("sort" in inglese significa "sorta", "specie" ma
# anche "ordinamento")
sort(alu)
[1] 140 145 146 147 147 149 150 152 152 153 153 154 155 155 156 157 158 161
c( min(alu), max(alu), length(alu), mean(alu), median(alu) )
[1] 140.0000 161.0000 18.0000 151.6667 152.5000
# Si noti che quando si stampano più dati usando c(...) essi vengono tutti
# scritti con cifre dopo il "." se ce n'è qualcuno che ne ha.
# Alla fine abbiamo stampato anche il valore della mediana ossia il valore
# che sta al centro dell'elenco.
#
# Ecco l'istogramma. Il programma sceglie automaticamente le classi in cui
# classificare i dati. Il comando è hist.
hist(alu, right=FALSE)
# L'espressione "right=FALSE" serve per comunicare al programma che vogliamo che gli
# intervalli siano del tipo […,…), in modo che ad esempio 150 non sia classificato
# tra 145 e 150 ma tra 150 e 155: 150 non sta in [145,150) ma sta in [150,155).
 # Vengono rappresentate le frequenze delle varie classi in cui sono stati
# suddivisi i dati. Se aggiungiamo probability=TRUE otteniamo la stessa figura
# (vedi immagine di sopra, a destra), ma cambia la scala verticale: sono
# rappresentate non le frequenze ma le frequenze relative unitarie (o densità di
# frequenza), ossia le frequenze relative divise per l'ampiezza degli intervalli.
hist(alu, right=FALSE, probability=TRUE, col="yellow"); abline(h=0.06,lty=3)
# Tra 150 e 155 c'erano 6 dati; i dati sono 18, quindi la frequenza relativa è
# 6/18 = 0.333… (cioè 33.333…%), e quella unitaria è 6/18/5 = 0.06666… = 6.7%.
#
# Come faccio a trovare frequenze assolute e quelle percentuali (ossia le
# frequenze relative in forma percentuale) facilmente? Ecco:
hist(alu,right=FALSE)$counts
[1] 1 5 6 5 1
hist(alu,right=FALSE)$counts/length(alu)*100
[1] 5.555556 27.777778 33.333333 27.777778 5.555556
#
#
# Volendo posso decidere una sequenza di classi in cui classificare i dati.
# Basta che usi seq(A,B,h) per classificarli tra A e B in classi ampie h.
# Utilizziamo i dati alu già impiegati in precedenza.
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
hist(alu, right=FALSE, seq(140,161,3))
# Vengono rappresentate le frequenze delle varie classi in cui sono stati
# suddivisi i dati. Se aggiungiamo probability=TRUE otteniamo la stessa figura
# (vedi immagine di sopra, a destra), ma cambia la scala verticale: sono
# rappresentate non le frequenze ma le frequenze relative unitarie (o densità di
# frequenza), ossia le frequenze relative divise per l'ampiezza degli intervalli.
hist(alu, right=FALSE, probability=TRUE, col="yellow"); abline(h=0.06,lty=3)
# Tra 150 e 155 c'erano 6 dati; i dati sono 18, quindi la frequenza relativa è
# 6/18 = 0.333… (cioè 33.333…%), e quella unitaria è 6/18/5 = 0.06666… = 6.7%.
#
# Come faccio a trovare frequenze assolute e quelle percentuali (ossia le
# frequenze relative in forma percentuale) facilmente? Ecco:
hist(alu,right=FALSE)$counts
[1] 1 5 6 5 1
hist(alu,right=FALSE)$counts/length(alu)*100
[1] 5.555556 27.777778 33.333333 27.777778 5.555556
#
#
# Volendo posso decidere una sequenza di classi in cui classificare i dati.
# Basta che usi seq(A,B,h) per classificarli tra A e B in classi ampie h.
# Utilizziamo i dati alu già impiegati in precedenza.
alu <- c(146,158,152,140,157,147,161,147,149,154,155,153,155,156,150,153,152,145)
hist(alu, right=FALSE, seq(140,161,3))
 # Per scritte sugli assi più piccole potrei mettere hist(…, cex.axis=0.88)
#
# Con summary ho una sintesi delle informazioni numeriche sui dati.
# Vengono stampati anche il 1° e il 3° quartile, cioè i dati che stanno
# a metà della prima metà e a metà della seconda metà dei dati; la
# mediana sarebbe il 2° quartile.
summary(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
# Volendo, se hai caricato il file seguente:
# source("http://macosa.dima.unige.it/r.R")
# hai gli stessi esiti e una loro rappresentazione grafica con:
statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
# Per scritte sugli assi più piccole potrei mettere hist(…, cex.axis=0.88)
#
# Con summary ho una sintesi delle informazioni numeriche sui dati.
# Vengono stampati anche il 1° e il 3° quartile, cioè i dati che stanno
# a metà della prima metà e a metà della seconda metà dei dati; la
# mediana sarebbe il 2° quartile.
summary(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
# Volendo, se hai caricato il file seguente:
# source("http://macosa.dima.unige.it/r.R")
# hai gli stessi esiti e una loro rappresentazione grafica con:
statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
 # in cui il "box" azzuro rappresenta i dati dal 1° al 3° quartile e i
# pallini rappresentano i valori che corrispondono a dove starebbero il
# 5º e il 95º dato se i dati, distribuiti in modo simile, fossero 100.
#
# Se abbiamo più dati da analizzare li mettiamo su più righe:
alu2 <- c(146,158,152,140,157,147,161,147,149,154,155,153,
155,156,150,153,152,145,158,140,147,149,155,156,153,145,
141,156,158,151,161,148,157,159,160,162,149,163,152,149,
157,155)
# Ecco la loro analisi statistica:
hist(alu2,right=FALSE)
hist(alu2,right=FALSE,seq(140,164,3))
# in cui il "box" azzuro rappresenta i dati dal 1° al 3° quartile e i
# pallini rappresentano i valori che corrispondono a dove starebbero il
# 5º e il 95º dato se i dati, distribuiti in modo simile, fossero 100.
#
# Se abbiamo più dati da analizzare li mettiamo su più righe:
alu2 <- c(146,158,152,140,157,147,161,147,149,154,155,153,
155,156,150,153,152,145,158,140,147,149,155,156,153,145,
141,156,158,151,161,148,157,159,160,162,149,163,152,149,
157,155)
# Ecco la loro analisi statistica:
hist(alu2,right=FALSE)
hist(alu2,right=FALSE,seq(140,164,3))
 summary(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
# Posso anche usare come sopra statistiche() fissando la stessa scala per alu e alu2,
# col comando boxAB:
BF=4;HF=1.2
boxAB=c(140,163); statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
boxAB=c(140,163); statistiche(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
I pallini sono il 5° e il 95° percentile
summary(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
# Posso anche usare come sopra statistiche() fissando la stessa scala per alu e alu2,
# col comando boxAB:
BF=4;HF=1.2
boxAB=c(140,163); statistiche(alu)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 147.5 152.5 151.7 155.0 161.0
I pallini sono il 5° e il 95° percentile
boxAB=c(140,163); statistiche(alu2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
140.0 149.0 153.0 152.6 157.0 163.0
I pallini sono il 5° e il 95° percentile
 #
# Ecco come possiamo confrontare graficamente i due insiemi di dati:
hist(alu,seq(140,164,3),angle=45,density=7,probability=TRUE)
hist(alu2,seq(140,164,3),probability=TRUE,add=TRUE,angle=135,density=10)
# Ho aggiunto add=TRUE al comando per tracciare il 2° istogramma.
#
# Ecco come possiamo confrontare graficamente i due insiemi di dati:
hist(alu,seq(140,164,3),angle=45,density=7,probability=TRUE)
hist(alu2,seq(140,164,3),probability=TRUE,add=TRUE,angle=135,density=10)
# Ho aggiunto add=TRUE al comando per tracciare il 2° istogramma.

 # La rappresentazione a destra è stata ottenuta con questi comandi.
#
# Volendo posso introdurre una quantità variabile di input direttamente
# da tastiera mediante il comando scan(file="",n=...) in cui al posto
# di ... occorre mettere i dati da leggere. Due esempi. Il primo (faccio
# la somma di 3 numeri):
numeri <- scan(file="", n=3); sum(numeri)
1: 3
2: 7
3: 5
Read 3 items
[1] 15
# Il secondo (introduco un numero N e, poi, una quantità N di dati, di
# cui viene calcolata la media):
nalu <- scan(file="",n=1); altalu <- scan(file="",n=nalu); mean(altalu)
1: 7
Read 1 item
1: 154
2: 156
3: 163
4: 170
5: 161
6: 156
7: 159
Read 7 items
[1] 159.8571
#
#
# Un altro esempio di come i comandi possono essere spezzati su più
# righe. Ecco le lunghezze di molte fave (ossia semi di fava) raccolte
# da una classe di alunni di 12 anni. Occorre copiare e incollare tutte
# le righe, da "fave <- c(" alla riga finale ")".
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
# e il loro istogramma
hist(fave,right=FALSE)
# La rappresentazione a destra è stata ottenuta con questi comandi.
#
# Volendo posso introdurre una quantità variabile di input direttamente
# da tastiera mediante il comando scan(file="",n=...) in cui al posto
# di ... occorre mettere i dati da leggere. Due esempi. Il primo (faccio
# la somma di 3 numeri):
numeri <- scan(file="", n=3); sum(numeri)
1: 3
2: 7
3: 5
Read 3 items
[1] 15
# Il secondo (introduco un numero N e, poi, una quantità N di dati, di
# cui viene calcolata la media):
nalu <- scan(file="",n=1); altalu <- scan(file="",n=nalu); mean(altalu)
1: 7
Read 1 item
1: 154
2: 156
3: 163
4: 170
5: 161
6: 156
7: 159
Read 7 items
[1] 159.8571
#
#
# Un altro esempio di come i comandi possono essere spezzati su più
# righe. Ecco le lunghezze di molte fave (ossia semi di fava) raccolte
# da una classe di alunni di 12 anni. Occorre copiare e incollare tutte
# le righe, da "fave <- c(" alla riga finale ")".
fave <- c(
1.35,1.65,1.80,1.40,1.65,1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,
1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,
1.55,1.70,1.55,1.70,1.55,1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,
1.80,1.60,1.80,1.60,1.80,1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,
1.70,1.75,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,
1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,
1.45,1.60,1.70,1.80,1.50,1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,
1.85,1.50,1.60,1.75,1.90,1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,
1.75,1.95,1.55,1.65,1.75,2.00,1.55,1.65,1.75,2.30,1.35,1.65,1.80,1.40,1.65,
1.80,1.40,1.65,1.85,1.40,1.65,1.85,1.50,1.65,1.90,1.50,1.65,1.90,1.50,1.65,
1.90,1.50,1.70,1.90,1.50,1.70,1.90,1.50,1.70,2.25,1.55,1.70,1.55,1.70,1.55,
1.70,1.60,1.70,1.60,1.75,1.60,1.75,1.60,1.80,1.60,1.80,1.60,1.80,1.60,1.80,
1.00,1.55,1.70,1.75,1.30,1.55,1.70,1.75,1.40,1.60,1.70,1.75,1.40,1.60,1.70,
1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,
1.70,1.80,1.40,1.60,1.70,1.80,1.40,1.60,1.70,1.80,1.45,1.60,1.70,1.80,1.50,
1.60,1.70,1.80,1.50,1.60,1.70,1.85,1.50,1.60,1.70,1.85,1.50,1.60,1.75,1.90,
1.50,1.60,1.75,1.90,1.50,1.65,1.75,1.90,1.55,1.65,1.75,1.95,1.55,1.65,1.75,
2.00,1.55,1.65,1.75,2.30
)
# e il loro istogramma
hist(fave,right=FALSE)
 # e quello delle frequenze relative, con aggiunte delle righe
# tratteggiate orizzontali:
hist(fave,right=FALSE,probability=TRUE)
abline(h=c(1/2, 1, 1.5, 2, 2.5), lty=3)
# e quello delle frequenze relative, con aggiunte delle righe
# tratteggiate orizzontali:
hist(fave,right=FALSE,probability=TRUE)
abline(h=c(1/2, 1, 1.5, 2, 2.5), lty=3)
 # (il 2.5% dei dati sta tra 1.6 e 1.7 e un altro 2.5% tra 1.7 e 1.8)
# La sintesi delle informazioni:
summary(fave)
# ovvero, caricato: source("http://macosa.dima.unige.it/r.R")
statistiche(fave)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 1.550 1.650 1.659 1.750 2.300
# (il 2.5% dei dati sta tra 1.6 e 1.7 e un altro 2.5% tra 1.7 e 1.8)
# La sintesi delle informazioni:
summary(fave)
# ovvero, caricato: source("http://macosa.dima.unige.it/r.R")
statistiche(fave)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 1.550 1.650 1.659 1.750 2.300
 #
# Volendo posso scegliere io gli estremi degli intervalli. Se non li scelgo
# di uguale ampiezza viene tracciato l'istogramma con le frequenze relative.
hist(fave,c(1,1.3,1.5,1.7,1.9,2.3))
#
# Volendo posso scegliere io gli estremi degli intervalli. Se non li scelgo
# di uguale ampiezza viene tracciato l'istogramma con le frequenze relative.
hist(fave,c(1,1.3,1.5,1.7,1.9,2.3))
 #
# I dati possono essere copiati da rete e incollati in R o possono essere
# caricati da rete. Un esempio (il file"t-sec.txt" nella cartella "R").
# Leggo alcune righe (ad es. 4) di un file (ne leggo poche in quanto il file può
# essere lunghissimo, ad es. contenere qualche migliaia di dati):
readLines("http://macosa.dima.unige.it/R/t-sec.txt",n=4)
#[1] "# misure (troncate ai centesimi di sec) della durata di 1 s cronometrata a mano"
#[2] "111"
#[3] "103"
#[4] "109"
# Vedo che sono singoli dati interi e che c'è 1 riga da saltare. Lo faccio col
# comando skip. I dati sono separati da "aCapo"; li leggo col comando "scan"
# (se fossero separati da, ad es., ";" aggiungerei sep=";" )
dati <- scan("http://macosa.dima.unige.it/R/t-sec.txt", skip=1)
# Read 47 items
# In alternativa, posso esaminare il file da un browser (programma per navigare
# in Internet), copiarlo e poi usare scan("clipboard", skip=1)
# Il comando str visualizza la struttura di oggetti. Lo uso per esaminare dati
str(dati)
# num [1:47] 111 103 109 97 99 110 99 103 109 106 ...
# sono 47 dati. I dati sono troncati agli interi. Per fare valutazioni corrette
# devo avere dati arrotondati: aggiungo 1/2
DATI <- dati+1/2
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.86 108.00 129.50
hist(DATI,right=FALSE,seq(65,135,10))
# visto il grafico, scelgo la scala verticale in modo da vedere la quota 25
hist(DATI,right=FALSE,seq(65,135,10),ylim=c(0,25))
abline(h=c(5,10,15,20,25), lty=3)
#
# I dati possono essere copiati da rete e incollati in R o possono essere
# caricati da rete. Un esempio (il file"t-sec.txt" nella cartella "R").
# Leggo alcune righe (ad es. 4) di un file (ne leggo poche in quanto il file può
# essere lunghissimo, ad es. contenere qualche migliaia di dati):
readLines("http://macosa.dima.unige.it/R/t-sec.txt",n=4)
#[1] "# misure (troncate ai centesimi di sec) della durata di 1 s cronometrata a mano"
#[2] "111"
#[3] "103"
#[4] "109"
# Vedo che sono singoli dati interi e che c'è 1 riga da saltare. Lo faccio col
# comando skip. I dati sono separati da "aCapo"; li leggo col comando "scan"
# (se fossero separati da, ad es., ";" aggiungerei sep=";" )
dati <- scan("http://macosa.dima.unige.it/R/t-sec.txt", skip=1)
# Read 47 items
# In alternativa, posso esaminare il file da un browser (programma per navigare
# in Internet), copiarlo e poi usare scan("clipboard", skip=1)
# Il comando str visualizza la struttura di oggetti. Lo uso per esaminare dati
str(dati)
# num [1:47] 111 103 109 97 99 110 99 103 109 106 ...
# sono 47 dati. I dati sono troncati agli interi. Per fare valutazioni corrette
# devo avere dati arrotondati: aggiungo 1/2
DATI <- dati+1/2
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.86 108.00 129.50
hist(DATI,right=FALSE,seq(65,135,10))
# visto il grafico, scelgo la scala verticale in modo da vedere la quota 25
hist(DATI,right=FALSE,seq(65,135,10),ylim=c(0,25))
abline(h=c(5,10,15,20,25), lty=3)
 #
# Un'ultima osservazione.
# Se dispongo di dati già classificati, in intervalli di diversa ampiezza,
# posso riccorrere al comando istoclas presente nel file richiamabile con:
source("http://macosa.dima.unige.it/r.R")
# Vedi qui per un esempio:
#
# Un'ultima osservazione.
# Se dispongo di dati già classificati, in intervalli di diversa ampiezza,
# posso riccorrere al comando istoclas presente nel file richiamabile con:
source("http://macosa.dima.unige.it/r.R")
# Vedi qui per un esempio:
 #
# Possiamo generare dei numeri a caso. Ad es.
runif(4, min=1, max=10)
# [posso ottenere 9.139260 3.747637 3.847650 2.825768]
# genera 4 numeri casuali distribuiti "uniformemente" nell'intervallo (1,10).
# Invece:
trunc(runif(10, min=1, max=7))
# [ottengo ad esempio 2 4 1 4 5 3 4 6 2 5; "trunc" tronca un numero agli interi]
# genera 10 numeri casuali interi compresi tra 1 e 6
# Vediamo il lancio, 10 mila volte, di due dadi "equi":
n <- 10000; dadi <- trunc(runif(n, min=1, max=7))+trunc(runif(n, min=1, max=7))
# I valori sono stati messi in "dadi". Eccone alcuni:
dadi[1]; dadi[1:10]
# [1] 7
# [1] 7 9 9 7 8 6 4 10 7 7
hist(dadi, seq(1.5,12.5,1),probability=TRUE,col="yellow")
abline(h=c(0.05,0.1,0.15), lty=3)
#
# Possiamo generare dei numeri a caso. Ad es.
runif(4, min=1, max=10)
# [posso ottenere 9.139260 3.747637 3.847650 2.825768]
# genera 4 numeri casuali distribuiti "uniformemente" nell'intervallo (1,10).
# Invece:
trunc(runif(10, min=1, max=7))
# [ottengo ad esempio 2 4 1 4 5 3 4 6 2 5; "trunc" tronca un numero agli interi]
# genera 10 numeri casuali interi compresi tra 1 e 6
# Vediamo il lancio, 10 mila volte, di due dadi "equi":
n <- 10000; dadi <- trunc(runif(n, min=1, max=7))+trunc(runif(n, min=1, max=7))
# I valori sono stati messi in "dadi". Eccone alcuni:
dadi[1]; dadi[1:10]
# [1] 7
# [1] 7 9 9 7 8 6 4 10 7 7
hist(dadi, seq(1.5,12.5,1),probability=TRUE,col="yellow")
abline(h=c(0.05,0.1,0.15), lty=3)
 # Le uscite possibili sono 6*6 = 36; avendo supposto il dado "equo" sono tutte
# equiprobabili, ossia con probabilità 1/36. Ad es. 3 può uscire in 2 casi:
# 1 e 2, 2 ed 1; quindi la probabilità che esca è 2*1/36, ossia 0.0555…; e con
# 10 mila lanci ho ottenuto una frequenza relativa è vicina a 0.0555…
# L'istogramma a destra è stato ottenuto col comando Istogramma:
noClassi=1; Istogramma(dadi, 1.5,12.5, 1)
# Frequenze e frequenze percentuali:
#277, 554, 857, 1084, 1442, 1663, 1337, 1126, 862, 532, 266
#2.77,5.54,8.57,10.84,14.42,16.63,13.37,11.26,8.62,5.32,2.66
# La freq. relativa di 3 è 5.54% (ossia 0.0554).
#
# Posso trovare anche probabilità relative a fenomeni non facilmente studiabili in
# modo teorico. Vediamo come studiare le uscite del lancio di una coppia di dadi
# equi, assumendo come uscita la differenza dei valori che escono, che può
# andare da 0 a 5. Ci aspettiamo che 5 sia l'uscita meno probabile (viene solo se
# escono un 6 ed un 1), ma non è facile valutare gli altri casi.
# Per fare la differenza posso prendere il valore assoluto della sottrazione della
# seconda uscita dalla prima.
n=1e7; dadi=abs(trunc(runif(n, min=1,max=7))-trunc(runif(n, min=1,max=7)))
Istogramma(dadi,-0.5,5.5,1)
Frequenze e frequenze percentuali:
1666379, 2778367, 2221573, 1665591, 1111816, 556274
16.66,27.78,22.22,16.66,11.12,5.56
# Le uscite possibili sono 6*6 = 36; avendo supposto il dado "equo" sono tutte
# equiprobabili, ossia con probabilità 1/36. Ad es. 3 può uscire in 2 casi:
# 1 e 2, 2 ed 1; quindi la probabilità che esca è 2*1/36, ossia 0.0555…; e con
# 10 mila lanci ho ottenuto una frequenza relativa è vicina a 0.0555…
# L'istogramma a destra è stato ottenuto col comando Istogramma:
noClassi=1; Istogramma(dadi, 1.5,12.5, 1)
# Frequenze e frequenze percentuali:
#277, 554, 857, 1084, 1442, 1663, 1337, 1126, 862, 532, 266
#2.77,5.54,8.57,10.84,14.42,16.63,13.37,11.26,8.62,5.32,2.66
# La freq. relativa di 3 è 5.54% (ossia 0.0554).
#
# Posso trovare anche probabilità relative a fenomeni non facilmente studiabili in
# modo teorico. Vediamo come studiare le uscite del lancio di una coppia di dadi
# equi, assumendo come uscita la differenza dei valori che escono, che può
# andare da 0 a 5. Ci aspettiamo che 5 sia l'uscita meno probabile (viene solo se
# escono un 6 ed un 1), ma non è facile valutare gli altri casi.
# Per fare la differenza posso prendere il valore assoluto della sottrazione della
# seconda uscita dalla prima.
n=1e7; dadi=abs(trunc(runif(n, min=1,max=7))-trunc(runif(n, min=1,max=7)))
Istogramma(dadi,-0.5,5.5,1)
Frequenze e frequenze percentuali:
1666379, 2778367, 2221573, 1665591, 1111816, 556274
16.66,27.78,22.22,16.66,11.12,5.56
 # Per n = 10^7 (così come per n = 10^6) ottengo che l'uscita più frequente è 1
# (27.78% di probabilità).
# A questo punto posso provare a studiare il problema anche teoricamente ...
#
# Questo era un esempio di simulazione. Per valutare la precisione della stima si
# può ricorrere al seguente comando:
Pr <- function(n) {f <- 0; for (i in 1:n) f <- f + ifelse(Evento(),1,0);
fr <- f/n; S <- sqrt(fr*(1-fr)/(n-1)); cat(fr, "+/-", 3*S,'\n') }
# Introdotte queste righe e messo in Evento() una rappresentazione di un fenomeno
# di cui si vuole valutare la probabilità che valga 1 se esso si verifica e 0
# altrimenti, valutiamo, riferendoci all'esempio precedente, la probabilità che
# lanciando una coppia di dadi equi la loro differenza sia 1.
Evento <- function() abs(floor(runif(1)*6)-floor(runif(1)*6)) == 1
Pr(1e4)
#0.2825 +/- 0.01350713
Pr(1e5)
#0.27771 +/- 0.004248885
Pr(1e6)
#0.277448 +/- 0.001343219
Pr(1e7)
#0.2777537 +/- 0.000424907
# Possiamo dedurre che la probabilità è 0.2825±0.0135, anzi … 0.2777537±0.000425,
# ovvero 0.27775±0.00043. Andando avanti (se ho tempo …) posso trovare valutazioni
# più precise (queste valutazioni non sono certe, ma sono probabili al 99.7%).
# Una valutazione più complessa:
# qual è la probabilità, pescando 10 carte da un mazzo da 40, di ottenere almeno un
# tris (cioè 3 o 4 carte dello stesso valore)?
Evento <- function() {
ca <- array(rep(0,40),dim=c(4,10)); nu <- array(rep(0,10),dim=10)
tris <- 0; for (i in 1:10)
{ripeti <- 1; while(ripeti==1)
{seme <- floor(runif(1)*4)+1; valore <- floor(runif(1)*10)+1;
if (ca[seme,valore]==0) ripeti <- 0 }
ca[seme,valore] <- 1; nu[valore] <- nu[valore]+1;
for(valore in 1:10)
if (nu[valore]==3 | nu[valore]==4) {tris <- 1; valore <- 10}
};
ifelse(tris==1,1,0) }
# Descritto l'evento, valutiamo la probabilità:
Pr(1e3)
#0.409 +/- 0.04666528
Pr(1e4)
#0.3765 +/- 0.01453596
Pr(1e5)
#0.38396 +/- 0.004613929
Pr(1e6) # Per questa uscita occorre aspettare qualche minuto
#0.384978 +/- 0.001459771
# La probabilità cercata è 0.3850±0.0015, ovvero (38.50±0.15)%.
#
# Volendo generare P uscite casuali intere diverse tra loro che cadono tra M,M+1,...,N
# (N = P-1) uso sample(M:N). Esempi
sample(14:20)
#14 16 20 15 17 19 18
# La cosa è utile in molte situazioni. Es.: un generico ordine in cui posso estrarre
# le tredici carte di cuori:
sample(1:13)
#4 9 12 3 13 7 10 11 5 6 2 1 8
# Posso estrarre (del tutto a caso) 4 numeri tra 1 e 13:
sample(1:13, 4)
#6 10 11 12
#
# I numeri generati con runif e sample appaiono distribuiti in modo del tutto casuale.
# In realtà posso ottenere la stessa sequenza di numeri se batto set.seed(n) ("poni
# il seme eguale a n") con il medesimo numero intero n. Esempio:
sample(5:10); set.seed(273); sample(5:10); set.seed(273); sample(5:10)
# 6 10 7 5 8 9
# 6 7 5 9 10 8
# 6 7 5 9 10 8
set.seed(273); sample(5:10,3)
# 6 7 5
# La cosa è ad es. utile per controllare dei procedimenti che si vogliono realizzare
# in cui si impiega il generatore di numeri casuali.
# Per approfondimenti su come "è fatto" il generatore di numeri casuali vedi qui.
#
# Con questi comandi sono stati realizzati anche Codifica(seme,testo) e Decodifica(…,…)
# per realizzare codifiche "segrete"; occorre mettere in "seme" un numero intero.
# Ecco qualche esempio (vedi qui se vuoi vedere come sono stati realizzati):
frase = "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
Codifica(314, frase)
# "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/"
Decodifica(314, "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/")
# "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
frase2 = "195/3 = 65"
Codifica(-10, frase2)
# "F!I74TXTSI"
Decodifica(-10, "F!I74TXTSI")
# "195/3 = 65"
#
#
# NOTA tecnica su come "salvare" i grafici e i comandi usati.
# Per memorizzare un'immagine posso cliccare su di essa e dal menu che si
# apre salvarla come BitMap e poi o
# -- incollarla direttamente in un documento del programma con cui si sta
# scrivendo (OpenOffice, LibreOffice, Wordpad, Word, ...) o
# -- incollarla in Paint (o un altro programma di grafica), aggiungere
# quello che si vuole, spostarla e ridurre i margini, e poi o
# - copiarla nell'eventuale documento in cui si sta scrivendo o,
# - da Paint, salvarla in formato PNG o GIF, che occupano poco spazio.
# Per memorizzare i comandi usati posso, dal menu File, azionare il comando
# Save History che consente di salvare in un file (in formato testo) tutti
# i comandi eseguiti (devo dare un nome al file; posso lasciargli la
# estensione "Rhistory" o mettere l'estensione "txt"). Poi, dopo, posso
# [ o caricare automaticamente i comandi dal file usando il comando Load
# History, che può essere usato anche per richiamare automaticamente
# comandi caricati in altri file, o ]
# aprire il file con BloccoNote (NotePad) o un altro editor e copiare e
# incollare in R la sequenza di comandi che voglio.
#
# Per un formulario completo di tutti i comandi vai qui.
#
# Per usi più avanzati (scarto quadratico medio, gaussiana, altre distribuzioni,
# tabelle di contingenza, …) vai qui. Ricordiamo solo che accanto ai comandi presenti
# nel software var(dati) e sd(dati), che calcolano varianza e deviazione standard (o
# scarto quadratico medio) "sperimentali", sono presenti, se hai caricato:
# source("http://macosa.dima.unige.it/r.R")
# i comandi Var(dati), Sd(dati) e SdM(dati) che calcolano la varianza, la deviazione
# standard (o scarto quadratico medio) "teorici" e la deviazione standard della media.
#
# Per n = 10^7 (così come per n = 10^6) ottengo che l'uscita più frequente è 1
# (27.78% di probabilità).
# A questo punto posso provare a studiare il problema anche teoricamente ...
#
# Questo era un esempio di simulazione. Per valutare la precisione della stima si
# può ricorrere al seguente comando:
Pr <- function(n) {f <- 0; for (i in 1:n) f <- f + ifelse(Evento(),1,0);
fr <- f/n; S <- sqrt(fr*(1-fr)/(n-1)); cat(fr, "+/-", 3*S,'\n') }
# Introdotte queste righe e messo in Evento() una rappresentazione di un fenomeno
# di cui si vuole valutare la probabilità che valga 1 se esso si verifica e 0
# altrimenti, valutiamo, riferendoci all'esempio precedente, la probabilità che
# lanciando una coppia di dadi equi la loro differenza sia 1.
Evento <- function() abs(floor(runif(1)*6)-floor(runif(1)*6)) == 1
Pr(1e4)
#0.2825 +/- 0.01350713
Pr(1e5)
#0.27771 +/- 0.004248885
Pr(1e6)
#0.277448 +/- 0.001343219
Pr(1e7)
#0.2777537 +/- 0.000424907
# Possiamo dedurre che la probabilità è 0.2825±0.0135, anzi … 0.2777537±0.000425,
# ovvero 0.27775±0.00043. Andando avanti (se ho tempo …) posso trovare valutazioni
# più precise (queste valutazioni non sono certe, ma sono probabili al 99.7%).
# Una valutazione più complessa:
# qual è la probabilità, pescando 10 carte da un mazzo da 40, di ottenere almeno un
# tris (cioè 3 o 4 carte dello stesso valore)?
Evento <- function() {
ca <- array(rep(0,40),dim=c(4,10)); nu <- array(rep(0,10),dim=10)
tris <- 0; for (i in 1:10)
{ripeti <- 1; while(ripeti==1)
{seme <- floor(runif(1)*4)+1; valore <- floor(runif(1)*10)+1;
if (ca[seme,valore]==0) ripeti <- 0 }
ca[seme,valore] <- 1; nu[valore] <- nu[valore]+1;
for(valore in 1:10)
if (nu[valore]==3 | nu[valore]==4) {tris <- 1; valore <- 10}
};
ifelse(tris==1,1,0) }
# Descritto l'evento, valutiamo la probabilità:
Pr(1e3)
#0.409 +/- 0.04666528
Pr(1e4)
#0.3765 +/- 0.01453596
Pr(1e5)
#0.38396 +/- 0.004613929
Pr(1e6) # Per questa uscita occorre aspettare qualche minuto
#0.384978 +/- 0.001459771
# La probabilità cercata è 0.3850±0.0015, ovvero (38.50±0.15)%.
#
# Volendo generare P uscite casuali intere diverse tra loro che cadono tra M,M+1,...,N
# (N = P-1) uso sample(M:N). Esempi
sample(14:20)
#14 16 20 15 17 19 18
# La cosa è utile in molte situazioni. Es.: un generico ordine in cui posso estrarre
# le tredici carte di cuori:
sample(1:13)
#4 9 12 3 13 7 10 11 5 6 2 1 8
# Posso estrarre (del tutto a caso) 4 numeri tra 1 e 13:
sample(1:13, 4)
#6 10 11 12
#
# I numeri generati con runif e sample appaiono distribuiti in modo del tutto casuale.
# In realtà posso ottenere la stessa sequenza di numeri se batto set.seed(n) ("poni
# il seme eguale a n") con il medesimo numero intero n. Esempio:
sample(5:10); set.seed(273); sample(5:10); set.seed(273); sample(5:10)
# 6 10 7 5 8 9
# 6 7 5 9 10 8
# 6 7 5 9 10 8
set.seed(273); sample(5:10,3)
# 6 7 5
# La cosa è ad es. utile per controllare dei procedimenti che si vogliono realizzare
# in cui si impiega il generatore di numeri casuali.
# Per approfondimenti su come "è fatto" il generatore di numeri casuali vedi qui.
#
# Con questi comandi sono stati realizzati anche Codifica(seme,testo) e Decodifica(…,…)
# per realizzare codifiche "segrete"; occorre mettere in "seme" un numero intero.
# Ecco qualche esempio (vedi qui se vuoi vedere come sono stati realizzati):
frase = "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
Codifica(314, frase)
# "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/"
Decodifica(314, "\"m%rfgmcew%c~~f%5(*-?%gcrcdqm%c%vcac%q|c6%\"mcw/")
# "Ci vediamo alle 17:30 davanti a casa tua. Ciao!"
frase2 = "195/3 = 65"
Codifica(-10, frase2)
# "F!I74TXTSI"
Decodifica(-10, "F!I74TXTSI")
# "195/3 = 65"
#
#
# NOTA tecnica su come "salvare" i grafici e i comandi usati.
# Per memorizzare un'immagine posso cliccare su di essa e dal menu che si
# apre salvarla come BitMap e poi o
# -- incollarla direttamente in un documento del programma con cui si sta
# scrivendo (OpenOffice, LibreOffice, Wordpad, Word, ...) o
# -- incollarla in Paint (o un altro programma di grafica), aggiungere
# quello che si vuole, spostarla e ridurre i margini, e poi o
# - copiarla nell'eventuale documento in cui si sta scrivendo o,
# - da Paint, salvarla in formato PNG o GIF, che occupano poco spazio.
# Per memorizzare i comandi usati posso, dal menu File, azionare il comando
# Save History che consente di salvare in un file (in formato testo) tutti
# i comandi eseguiti (devo dare un nome al file; posso lasciargli la
# estensione "Rhistory" o mettere l'estensione "txt"). Poi, dopo, posso
# [ o caricare automaticamente i comandi dal file usando il comando Load
# History, che può essere usato anche per richiamare automaticamente
# comandi caricati in altri file, o ]
# aprire il file con BloccoNote (NotePad) o un altro editor e copiare e
# incollare in R la sequenza di comandi che voglio.
#
# Per un formulario completo di tutti i comandi vai qui.
#
# Per usi più avanzati (scarto quadratico medio, gaussiana, altre distribuzioni,
# tabelle di contingenza, …) vai qui. Ricordiamo solo che accanto ai comandi presenti
# nel software var(dati) e sd(dati), che calcolano varianza e deviazione standard (o
# scarto quadratico medio) "sperimentali", sono presenti, se hai caricato:
# source("http://macosa.dima.unige.it/r.R")
# i comandi Var(dati), Sd(dati) e SdM(dati) che calcolano la varianza, la deviazione
# standard (o scarto quadratico medio) "teorici" e la deviazione standard della media.
#