source("http://macosa.dima.unige.it/r.R") # If I have not already loaded the library
---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
S 03 Vector Calculus
 [prodv (or crossp) prods (or dotp) modulus (or magnitude) versor; see also J-2, #J]
# dot product or scalar product, and (only in three-dimensional space) cross product or
# vector product
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# The sum of vectors is done with "+" (If I represent them with arrow, not with Arrow,
# where - as we have seen - I put the vectors as "direction" and "modulus" instead of
# as "x" and "y":
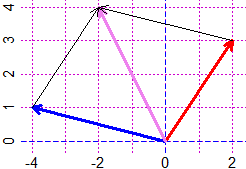
v1 <- c(2,3); v2 <- c(-4,1)
PLANE(-4,2, -1,5)
arrow(0,0,v1[1],v1[2], "red")
arrow(0,0,v2[1],v2[2], "blue")
arrow(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
dart(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
dart(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# I remember putting 1 as a color is equivalent to putting "black"
[prodv (or crossp) prods (or dotp) modulus (or magnitude) versor; see also J-2, #J]
# dot product or scalar product, and (only in three-dimensional space) cross product or
# vector product
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# The sum of vectors is done with "+" (If I represent them with arrow, not with Arrow,
# where - as we have seen - I put the vectors as "direction" and "modulus" instead of
# as "x" and "y":
v1 <- c(2,3); v2 <- c(-4,1)
PLANE(-4,2, -1,5)
arrow(0,0,v1[1],v1[2], "red")
arrow(0,0,v2[1],v2[2], "blue")
arrow(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
dart(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
dart(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# I remember putting 1 as a color is equivalent to putting "black"
 # The direction and the length of the red arrow:
dirArrow(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# Its versor and, with another command, its length:
versor(v1); modulus(v1)
# 0.5547002 0.8320503 3.605551
Other examples of use
# The direction and the length of the red arrow:
dirArrow(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# Its versor and, with another command, its length:
versor(v1); modulus(v1)
# 0.5547002 0.8320503 3.605551
Other examples of use
 [prodv (or crossp) prods (or dotp) modulus (or magnitude) versor; see also J-2, #J]
# dot product or scalar product, and (only in three-dimensional space) cross product or
# vector product
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# The sum of vectors is done with "+" (If I represent them with arrow, not with Arrow,
# where - as we have seen - I put the vectors as "direction" and "modulus" instead of
# as "x" and "y":
v1 <- c(2,3); v2 <- c(-4,1)
PLANE(-4,2, -1,5)
arrow(0,0,v1[1],v1[2], "red")
arrow(0,0,v2[1],v2[2], "blue")
arrow(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
dart(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
dart(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# I remember putting 1 as a color is equivalent to putting "black"
[prodv (or crossp) prods (or dotp) modulus (or magnitude) versor; see also J-2, #J]
# dot product or scalar product, and (only in three-dimensional space) cross product or
# vector product
v1 <- c(1,-2,2); v2 <- c(-4,0,2); prods(v1,v2); prodv(v1,v2)
# 0 -4 -10 -8
v1 <- c(1,-2,2); v2 <- c(-4,1,2); prods(v1,v2); prodv(v1,v2)
# -2 -6 -10 -7
v1 <- c(0,0,1); v2 <- c(1,0,0); prods(v1,v2); prodv(v1,v2)
# 0 0 1 0
# The sum of vectors is done with "+" (If I represent them with arrow, not with Arrow,
# where - as we have seen - I put the vectors as "direction" and "modulus" instead of
# as "x" and "y":
v1 <- c(2,3); v2 <- c(-4,1)
PLANE(-4,2, -1,5)
arrow(0,0,v1[1],v1[2], "red")
arrow(0,0,v2[1],v2[2], "blue")
arrow(0,0,(v1+v2)[1],(v1+v2)[2], "violet")
dart(v1[1],v1[2], (v1+v2)[1],(v1+v2)[2], 1)
dart(v2[1],v2[2], (v1+v2)[1],(v1+v2)[2], 1)
# I remember putting 1 as a color is equivalent to putting "black"
 # The direction and the length of the red arrow:
dirArrow(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# Its versor and, with another command, its length:
versor(v1); modulus(v1)
# 0.5547002 0.8320503 3.605551
Other examples of use
# The direction and the length of the red arrow:
dirArrow(0,0, v1[1],v1[2])
# direz. = 56.30993 ° lungh. = 3.605551
# Its versor and, with another command, its length:
versor(v1); modulus(v1)
# 0.5547002 0.8320503 3.605551
Other examples of use