source("http://macosa.dima.unige.it/r.R") # If I have not already loaded the library
---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
S 04 Lenghts and Areas
# areaF(f, a,b, N) (or areaFun) calculates the area of the N-gon that approximates the
# graph of f.
# Examples for N = 2, 4, 10 thousand, 100 thousand for a certain f
BF=3; HF=2
f <- function(x) sqrt(1-x^2)
PLANE(-1,1, 0,1); areaF(f,-1,1,2) # 1
PLANE(-1,1, 0,1); areaF(f,-1,1,4) # 1.3660254
PLANE(-1,1, 0,1); areaF(f,-1,1,1e4) # 1.5707947
# Use areaF2 if (for great N) you want a faster computation
PLANE(-1,1, 0,1); areaF2(f,-1,1,1e5) # 1.5707963 (=π/2)
# Another example (graphs on the left):
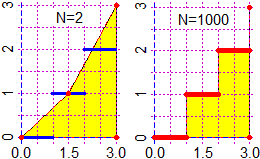
Plane(0,3,0,3); areaF(floor, 0,3, 2) # 3.75
Plane(0,3,0,3); areaF(floor, 0,3, 1000) # 3.0015
Plane(0,3,0,3); areaF2(floor, 0,3, 1e4) # 3.00015
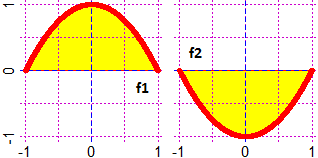# The areas are signed: positive/negative if they are above/below the x axis
# (graphs above on the right)
f1 <- function(x) -x^2+1; f2 <- function(x) -f1(x)
BF=3; HF=3
PLANE(-1,1, -1,1); areaF(f1,-1,1,2000) # 1.333333
PLANE(-1,1, -1,1); areaF(f2,-1,1,2000) # -1.333333
#
# I can calculate the area of the polygon that is under the graph of a piecewise linear
# function (with coordinates in x and y), using the areaPol command, if I define the
# function AREA (but I can use another name) in this way:
AREA = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
# Example:
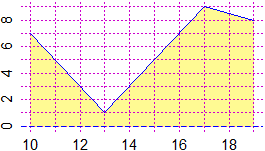x = c(10,13, 17, 19); y = c(7,1,9,8)
Plane(min(x),max(x), 0,max(y)); polyl(x,y,"blue")
AREA = function(x,y) areaPol( c(x[length(x)],x[1],x), c(0,0,y) )
AREA(x,y) # 49
#
# areaPar(x,y, a,b, N), areaPolar(r, a,b, N) calculate the area enclosed by a curve
# in parametric form and polar form (see S01). To calculate the length of a curve (when
# it is finite), I use lengFun(f,a,b,N), lengPar(x,y,a,b,N) or lengPolar(r,a,b,N)
# depending on how it is defined. lengPar3(x,y,z,a,b,N) works analogously in the case
# of a curve in the space. [N is the number of sides of the polygonal chain
that approximates the curve]
# As can be seen in S08, to calculate the area of figures, integration can be used.
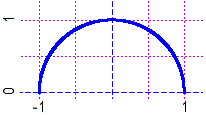
# Examples for calculating the length of the semicircle (in various ways):
| |
3.141593 | |
 |
length = 24
area = 6 π
|
 |
# as a function (input: f, A,B, N)
f = function(x) sqrt(1-x^2)
# in a parametric representation (input: f,g, A,B, N)
x = function(t) cos(t); y = function(t) sin(t)
# as a polar equation (input: r, A,B, N)
# (in this particular case r does not depend on ang)
r = function(ang) 1
lengFun(f, -1,1, 100); lengFun(f, -1,1, 10000); lengFun(f, -1,1, 100000)
# 3.140761 3.141592 3.141593
lengPar(x,y, 0,pi, 100); lengPar(x,y, 0,pi, 1000); lengPar(x,y, 0,pi, 10000)
# 3.141463 3.141591 3.141593
lengPolar(r, 0,pi, 100); lengPolar(r, 0,pi, 1000); lengPolar(r, 0,pi, 10000)
# 3.141463 3.141591 3.141593
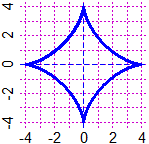
# Length and area of asteroid
# asteroid of "radius" 4
f = function(t) 4*cos(t)^3; g = function(t) 4*sin(t)^3
PLANE(-4,4, -4,4); param(f,g, 0,2*pi, "blue") # (graph above on the right)
lengPar(f,g,0,2*pi, 5000)
# 24
A = areaPar(f,g, 0,2*pi,5000); A
# 18.84957
A = areaPar(f,g, 0,2*pi,10000); A
# 18.84956
A/pi
# 6
# For the length of three-dimensional curves, see here.
#
# See here for areas enclosed by curves expressible only in Cartesian form.
# ( startP() xClick yClick )
#
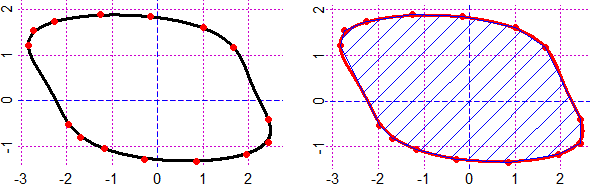# See here for a continuous function in a finite closed interval that has an infinite
# length graph and neither right nor left derivative.
# and for ...
# and a continuous function that is not derivable at any point
Other examples of use