---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
# Vediamo, per esteso, un esercizio non facile da risolvere a mano (e neanche con
# WoframAlpha, che, come gran parte del software di calcolo simbolico, non è affidabi-
# lissimo per lo studio di funzioni in quanto occorre usare dei trucchi per operare con
# le potenze ad esponente dispari e per evitare che siano fatte semplificazioni non le-
# cite, del tipo, per intenderci, √-1 / √-1 → 1).
#
# Sudiare il grafico della funzione x → (x/4)2/3 - (x-4)1/3 individuando
# punti di minimo e massimo (relativi) e cambi di concavità
#
# Innazi tutto mi pongo il problema che per il software z^a è definito solo per z ≥ 0;
# allora uso rad3 che in questa versione di R è definita ovunque:
g = function(x) rad3((x/4)^2) - rad3(x-4)
# eventualmente dopo aver caricato: source("http://macosa.dima.unige.it/r.R")
#
# Faccio prima lo studio graficamente, senza "calcoli"
# (qui ho messo HF=2.7; BF=2.7 per avere una finestra piccola)
# Inizio con un intervallo ampio, e poi mi restringo
graficoF( g, -100,100, 1)
# Ottengo il primo grafico sotto a sinistra.
# Per avere conferma che per x che cresce o decresce g(x) tende a crescere oltre ogni
# limite facciamo delle prove numeriche (provo con 10, 100, 1000, ... e -10, -100,
# -1000, ..., e arrorondo gli output per scriverli accorciati)
n=1:12; round(g(10^n))
# [1] 0 4 30 163 809 3869 18205 85035 395850 1839861 8545238 39675026
n=1:12; round(g(-10^n))
# [1] 4 13 50 206 901 4069 18636 85963 397850 1844170 8554521 39695026
# Si vede che in entrambi i casi gli output si moltiplicano circa per 100 al moltipli-
# carsi dell'input per 1000. OK [posso dire che cresce come |x|^(2/3), cosa capibile
# dall'espressione di g(x) in quanto 2^3 > 1/3 (vedi in fondo i grafici in un intervallo
# più ampio)]. Formalizzando, il limite per x → Inf e per x → -Inf è Inf.
# Posso dunque restringere l'intervallo degli input:
graficoF( g, -10,100, 1)
# Ottengo il secondo grafico.
 # Ho segnato in rosso quelli che, a prima vista, potrebbero essere i punti cercati.
# Vediamo prima la parte sinistra del grafico di g.
graficoF( g, -2,12, 1)
# Ottengo il grafico sopra a destra.
# Il grafico viene fatto per punti: il tratto verticale punteggiato non significa che
# ivi la funzione non sia continua. Posso verificarlo con degli zoom:
graficoF( g, 3.9,4.1, 1)
# Ho segnato in rosso quelli che, a prima vista, potrebbero essere i punti cercati.
# Vediamo prima la parte sinistra del grafico di g.
graficoF( g, -2,12, 1)
# Ottengo il grafico sopra a destra.
# Il grafico viene fatto per punti: il tratto verticale punteggiato non significa che
# ivi la funzione non sia continua. Posso verificarlo con degli zoom:
graficoF( g, 3.9,4.1, 1)

 # Ottengo il grafico soprastante a sinistra.
#
# Intuisco, guardando l'espressione di g(x), che per x=0 e x=4 (dove x/4 e x-4 cambia-
# no segno) ho dei punti critici, in cui ci sono un minimo relativo e un cambio di con-
# cavità (flesso). Per studiare che cosa accade a destra di 12 mi converrà effettuare
# il calcolo delle derivate. Vediamo che cosa possiamo fare a sinistra senza di esse.
#
h = minmax(g, -2,2); h; g(h)
# [1] -1.589587e-14 "praticamente" 0
# [1] 1.587401
# Provo a mettere 1.587401 in WolframAlpha, e vedo che è un'approssimazione di 2^(2/3)
# Verifico: g(0) = rad3(4), ovvero 4^(1/3), ovvero (2^2)^(1/3) = 2^(2*1/3) = 2^(2/3)
# Dunque A = (0,rad3(4)) è un punto di minimo relativo
#
# Per x=4 g(x)=1. Come intuisco dal grafico dunque in C = (4,1) ho un flesso verticale.
#
# Troviamo B e D:
j = minmax(g, 1,3); j; g(j); k = minmax(g, 5,10); k; g(k)
# [1] 2
# [1] 1.889882
# [1] 8
# [1] 0
# Se metto 1.889882 in WolframAlpha vedo che è un'approssimazione di 3/2^(2/3)
# [=3*2^(1/3)/2]. Posso (come sopra) verificare la cosa. B = (2,3*rad3(2)/2) è un punto
# di massimo relativo. Invece D = (8,0) è un punto di minimo relativo.
#
# Studiamo la parte del grafico a destra del punto D.
# C'è un punto di flesso obliquo? Sopra ho segnato un ipotetico punto E di tal genere.
# Per verificare la cosa devo calcolare le derivate prima e vedere dove questa cresce o
# decresce (o devo calcolare la derivata seconda). Faccio entrambe le cose con R.
# Ne approffitto anche per studiare in questo modo i problemi già risolti sopra.
# Posso calcolare la derivata di g con derivata(g,"x"); per salvarla come funzione
# posso fare: dfg <- function(x) eval(derivata(g,"x"))
derivata(g,"x")
# Error: 'rad3' non presente nelle tavole delle derivate
# rad3 l'ho definita io; mi conviene spezzare la funzione a destra e sinistra di 4,
# dove l'input di rad3(x-4) cambia segno.
g1 = function(x) ((x/4)^2)^(1/3)+(4-x)^(1/3)
g2 = function(x) ((x/4)^2)^(1/3)-(x-4)^(1/3)
# Verifico graficamente la cosa.
HF=2.7; BF=2.7
graficoF( g, -2,12, 1)
grafico( g1, -2,4, "red")
grafico( g2, 4,12, "blue")
# OK
# Ottengo il grafico soprastante a sinistra.
#
# Intuisco, guardando l'espressione di g(x), che per x=0 e x=4 (dove x/4 e x-4 cambia-
# no segno) ho dei punti critici, in cui ci sono un minimo relativo e un cambio di con-
# cavità (flesso). Per studiare che cosa accade a destra di 12 mi converrà effettuare
# il calcolo delle derivate. Vediamo che cosa possiamo fare a sinistra senza di esse.
#
h = minmax(g, -2,2); h; g(h)
# [1] -1.589587e-14 "praticamente" 0
# [1] 1.587401
# Provo a mettere 1.587401 in WolframAlpha, e vedo che è un'approssimazione di 2^(2/3)
# Verifico: g(0) = rad3(4), ovvero 4^(1/3), ovvero (2^2)^(1/3) = 2^(2*1/3) = 2^(2/3)
# Dunque A = (0,rad3(4)) è un punto di minimo relativo
#
# Per x=4 g(x)=1. Come intuisco dal grafico dunque in C = (4,1) ho un flesso verticale.
#
# Troviamo B e D:
j = minmax(g, 1,3); j; g(j); k = minmax(g, 5,10); k; g(k)
# [1] 2
# [1] 1.889882
# [1] 8
# [1] 0
# Se metto 1.889882 in WolframAlpha vedo che è un'approssimazione di 3/2^(2/3)
# [=3*2^(1/3)/2]. Posso (come sopra) verificare la cosa. B = (2,3*rad3(2)/2) è un punto
# di massimo relativo. Invece D = (8,0) è un punto di minimo relativo.
#
# Studiamo la parte del grafico a destra del punto D.
# C'è un punto di flesso obliquo? Sopra ho segnato un ipotetico punto E di tal genere.
# Per verificare la cosa devo calcolare le derivate prima e vedere dove questa cresce o
# decresce (o devo calcolare la derivata seconda). Faccio entrambe le cose con R.
# Ne approffitto anche per studiare in questo modo i problemi già risolti sopra.
# Posso calcolare la derivata di g con derivata(g,"x"); per salvarla come funzione
# posso fare: dfg <- function(x) eval(derivata(g,"x"))
derivata(g,"x")
# Error: 'rad3' non presente nelle tavole delle derivate
# rad3 l'ho definita io; mi conviene spezzare la funzione a destra e sinistra di 4,
# dove l'input di rad3(x-4) cambia segno.
g1 = function(x) ((x/4)^2)^(1/3)+(4-x)^(1/3)
g2 = function(x) ((x/4)^2)^(1/3)-(x-4)^(1/3)
# Verifico graficamente la cosa.
HF=2.7; BF=2.7
graficoF( g, -2,12, 1)
grafico( g1, -2,4, "red")
grafico( g2, 4,12, "blue")
# OK  dg1 <- function(x) eval( derivata(g1,"x") )
soluz(dg1,0, 1,3)
# [1] 2
dg2 <- function(x) eval( derivata(g2,"x") )
soluz(dg2,0, 5,10)
# [1] 8
# Ho ritrovato B e D. Ma sono proprio gli stessi valori?
piu( minmax(g, 1,3) ); piu(soluz(dg1,0, 1,3))
# 1.99999998773738 2
# Il secondo metodo è più preciso in quanto l'algoritmo per trovare il minimo e il
# massimo senza ricorrere alla derivate (pur essendo più generale) è più approssimativo
# (ma sono differenze che dal punto di vista applicativo sono in genere trascurabili).
#
# Per trovare E posso studiare dove cresce/decresce D(g)
maxmin(dg2,10,100)
# [1] 31.52936
# Oppure posso studiare dove si azzera la derivata 2^a
d2g2 <- function(x) eval( derivata2(g2,"x") )
soluz(d2g2,0, 10,100)
# [1] 31.52936
# Ho trovato lo stesso valore. In realtà i due procedimenti non danno gli stessi valori:
piu( maxmin(dg2,10,100) ); piu( soluz(d2g2,0, 10,100) )
# 31.5293616373527 31.5293611968877
# Anche in questo caso il secondo metodo dà un risultato più preciso.
# La y corrispondente è:
g( soluz(d2g2,0, 10,100) )
# [1] 0.9412041
# Dunque E = (31.52936, 0.9412041)
#
# Volendo potrei calcolare le derivate a mano, o con R. Con derivata(g2,"x") ho:
# ((x/4)^2)^((1/3)-1)*((1/3)*(2*(1/4*(x/4))))-(x-4)^((1/3)-1)*(1/3) che posso sempli-
# ficare in (x/4)^(-1/3)/6 - (x-4)^(-2/3)/3 ... o posso usare WolgramAlpha. Se
# metto: solve ( d/dx d/dx ((x/4)^2)^(1/3)-(x-4)^(1/3) ) = 0
# ottengo 31.52936119688764498693379…
#
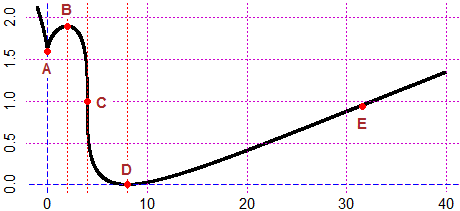
# Ecco come è stato ottenuto il grafico con le soluzioni:
HF=2.7; BF=2.7*2
graficoF( g, -1,40, 1)
grafico ( g, 3,5, 1)
a = 0; b = 2; c = 4; d = 8; e = soluz(d2g2,0, 10,100)
PUNTO( c(a,b,c,d,e), g( c(a,b,c,d,e) ), "red")
# altro:
coltrat="red"; grigliaV(2); grigliaV(4); grigliaV(8)
scrivi(0,1.4,"A"); scrivi(2,2.1,"B"); scrivi(5.5,1,"C")
scrivi(8,0.2,"D"); scrivi(31.53,0.75,"E")
(l'esempio è tratto da "Complementi ed esercizi di Analisi Matematica" di Aldo Ghizzetti)
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Confronto di g con:
f = function(x) abs(x)^(2/3)
graficoF (g, -1e5,1e5, "black"); graficoF (f, -1e5,1e5, "brown")
dg1 <- function(x) eval( derivata(g1,"x") )
soluz(dg1,0, 1,3)
# [1] 2
dg2 <- function(x) eval( derivata(g2,"x") )
soluz(dg2,0, 5,10)
# [1] 8
# Ho ritrovato B e D. Ma sono proprio gli stessi valori?
piu( minmax(g, 1,3) ); piu(soluz(dg1,0, 1,3))
# 1.99999998773738 2
# Il secondo metodo è più preciso in quanto l'algoritmo per trovare il minimo e il
# massimo senza ricorrere alla derivate (pur essendo più generale) è più approssimativo
# (ma sono differenze che dal punto di vista applicativo sono in genere trascurabili).
#
# Per trovare E posso studiare dove cresce/decresce D(g)
maxmin(dg2,10,100)
# [1] 31.52936
# Oppure posso studiare dove si azzera la derivata 2^a
d2g2 <- function(x) eval( derivata2(g2,"x") )
soluz(d2g2,0, 10,100)
# [1] 31.52936
# Ho trovato lo stesso valore. In realtà i due procedimenti non danno gli stessi valori:
piu( maxmin(dg2,10,100) ); piu( soluz(d2g2,0, 10,100) )
# 31.5293616373527 31.5293611968877
# Anche in questo caso il secondo metodo dà un risultato più preciso.
# La y corrispondente è:
g( soluz(d2g2,0, 10,100) )
# [1] 0.9412041
# Dunque E = (31.52936, 0.9412041)
#
# Volendo potrei calcolare le derivate a mano, o con R. Con derivata(g2,"x") ho:
# ((x/4)^2)^((1/3)-1)*((1/3)*(2*(1/4*(x/4))))-(x-4)^((1/3)-1)*(1/3) che posso sempli-
# ficare in (x/4)^(-1/3)/6 - (x-4)^(-2/3)/3 ... o posso usare WolgramAlpha. Se
# metto: solve ( d/dx d/dx ((x/4)^2)^(1/3)-(x-4)^(1/3) ) = 0
# ottengo 31.52936119688764498693379…
#
# Ecco come è stato ottenuto il grafico con le soluzioni:
HF=2.7; BF=2.7*2
graficoF( g, -1,40, 1)
grafico ( g, 3,5, 1)
a = 0; b = 2; c = 4; d = 8; e = soluz(d2g2,0, 10,100)
PUNTO( c(a,b,c,d,e), g( c(a,b,c,d,e) ), "red")
# altro:
coltrat="red"; grigliaV(2); grigliaV(4); grigliaV(8)
scrivi(0,1.4,"A"); scrivi(2,2.1,"B"); scrivi(5.5,1,"C")
scrivi(8,0.2,"D"); scrivi(31.53,0.75,"E")
(l'esempio è tratto da "Complementi ed esercizi di Analisi Matematica" di Aldo Ghizzetti)
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Confronto di g con:
f = function(x) abs(x)^(2/3)
graficoF (g, -1e5,1e5, "black"); graficoF (f, -1e5,1e5, "brown")
 # Si vede che per x che tende a Inf e a -Inf entrambe le curve salgono oltre ogni
# limite e con la concavità verso il basso.
# Si vede che per x che tende a Inf e a -Inf entrambe le curve salgono oltre ogni
# limite e con la concavità verso il basso.
 # Ho segnato in rosso quelli che, a prima vista, potrebbero essere i punti cercati.
# Vediamo prima la parte sinistra del grafico di g.
graficoF( g, -2,12, 1)
# Ottengo il grafico sopra a destra.
# Il grafico viene fatto per punti: il tratto verticale punteggiato non significa che
# ivi la funzione non sia continua. Posso verificarlo con degli zoom:
graficoF( g, 3.9,4.1, 1)
# Ho segnato in rosso quelli che, a prima vista, potrebbero essere i punti cercati.
# Vediamo prima la parte sinistra del grafico di g.
graficoF( g, -2,12, 1)
# Ottengo il grafico sopra a destra.
# Il grafico viene fatto per punti: il tratto verticale punteggiato non significa che
# ivi la funzione non sia continua. Posso verificarlo con degli zoom:
graficoF( g, 3.9,4.1, 1)

 # Ottengo il grafico soprastante a sinistra.
#
# Intuisco, guardando l'espressione di g(x), che per x=0 e x=4 (dove x/4 e x-4 cambia-
# no segno) ho dei punti critici, in cui ci sono un minimo relativo e un cambio di con-
# cavità (flesso). Per studiare che cosa accade a destra di 12 mi converrà effettuare
# il calcolo delle derivate. Vediamo che cosa possiamo fare a sinistra senza di esse.
#
h = minmax(g, -2,2); h; g(h)
# [1] -1.589587e-14 "praticamente" 0
# [1] 1.587401
# Provo a mettere 1.587401 in WolframAlpha, e vedo che è un'approssimazione di 2^(2/3)
# Verifico: g(0) = rad3(4), ovvero 4^(1/3), ovvero (2^2)^(1/3) = 2^(2*1/3) = 2^(2/3)
# Dunque A = (0,rad3(4)) è un punto di minimo relativo
#
# Per x=4 g(x)=1. Come intuisco dal grafico dunque in C = (4,1) ho un flesso verticale.
#
# Troviamo B e D:
j = minmax(g, 1,3); j; g(j); k = minmax(g, 5,10); k; g(k)
# [1] 2
# [1] 1.889882
# [1] 8
# [1] 0
# Se metto 1.889882 in WolframAlpha vedo che è un'approssimazione di 3/2^(2/3)
# [=3*2^(1/3)/2]. Posso (come sopra) verificare la cosa. B = (2,3*rad3(2)/2) è un punto
# di massimo relativo. Invece D = (8,0) è un punto di minimo relativo.
#
# Studiamo la parte del grafico a destra del punto D.
# C'è un punto di flesso obliquo? Sopra ho segnato un ipotetico punto E di tal genere.
# Per verificare la cosa devo calcolare le derivate prima e vedere dove questa cresce o
# decresce (o devo calcolare la derivata seconda). Faccio entrambe le cose con R.
# Ne approffitto anche per studiare in questo modo i problemi già risolti sopra.
# Posso calcolare la derivata di g con derivata(g,"x"); per salvarla come funzione
# posso fare: dfg <- function(x) eval(derivata(g,"x"))
derivata(g,"x")
# Error: 'rad3' non presente nelle tavole delle derivate
# rad3 l'ho definita io; mi conviene spezzare la funzione a destra e sinistra di 4,
# dove l'input di rad3(x-4) cambia segno.
g1 = function(x) ((x/4)^2)^(1/3)+(4-x)^(1/3)
g2 = function(x) ((x/4)^2)^(1/3)-(x-4)^(1/3)
# Verifico graficamente la cosa.
HF=2.7; BF=2.7
graficoF( g, -2,12, 1)
grafico( g1, -2,4, "red")
grafico( g2, 4,12, "blue")
# OK
# Ottengo il grafico soprastante a sinistra.
#
# Intuisco, guardando l'espressione di g(x), che per x=0 e x=4 (dove x/4 e x-4 cambia-
# no segno) ho dei punti critici, in cui ci sono un minimo relativo e un cambio di con-
# cavità (flesso). Per studiare che cosa accade a destra di 12 mi converrà effettuare
# il calcolo delle derivate. Vediamo che cosa possiamo fare a sinistra senza di esse.
#
h = minmax(g, -2,2); h; g(h)
# [1] -1.589587e-14 "praticamente" 0
# [1] 1.587401
# Provo a mettere 1.587401 in WolframAlpha, e vedo che è un'approssimazione di 2^(2/3)
# Verifico: g(0) = rad3(4), ovvero 4^(1/3), ovvero (2^2)^(1/3) = 2^(2*1/3) = 2^(2/3)
# Dunque A = (0,rad3(4)) è un punto di minimo relativo
#
# Per x=4 g(x)=1. Come intuisco dal grafico dunque in C = (4,1) ho un flesso verticale.
#
# Troviamo B e D:
j = minmax(g, 1,3); j; g(j); k = minmax(g, 5,10); k; g(k)
# [1] 2
# [1] 1.889882
# [1] 8
# [1] 0
# Se metto 1.889882 in WolframAlpha vedo che è un'approssimazione di 3/2^(2/3)
# [=3*2^(1/3)/2]. Posso (come sopra) verificare la cosa. B = (2,3*rad3(2)/2) è un punto
# di massimo relativo. Invece D = (8,0) è un punto di minimo relativo.
#
# Studiamo la parte del grafico a destra del punto D.
# C'è un punto di flesso obliquo? Sopra ho segnato un ipotetico punto E di tal genere.
# Per verificare la cosa devo calcolare le derivate prima e vedere dove questa cresce o
# decresce (o devo calcolare la derivata seconda). Faccio entrambe le cose con R.
# Ne approffitto anche per studiare in questo modo i problemi già risolti sopra.
# Posso calcolare la derivata di g con derivata(g,"x"); per salvarla come funzione
# posso fare: dfg <- function(x) eval(derivata(g,"x"))
derivata(g,"x")
# Error: 'rad3' non presente nelle tavole delle derivate
# rad3 l'ho definita io; mi conviene spezzare la funzione a destra e sinistra di 4,
# dove l'input di rad3(x-4) cambia segno.
g1 = function(x) ((x/4)^2)^(1/3)+(4-x)^(1/3)
g2 = function(x) ((x/4)^2)^(1/3)-(x-4)^(1/3)
# Verifico graficamente la cosa.
HF=2.7; BF=2.7
graficoF( g, -2,12, 1)
grafico( g1, -2,4, "red")
grafico( g2, 4,12, "blue")
# OK  dg1 <- function(x) eval( derivata(g1,"x") )
soluz(dg1,0, 1,3)
# [1] 2
dg2 <- function(x) eval( derivata(g2,"x") )
soluz(dg2,0, 5,10)
# [1] 8
# Ho ritrovato B e D. Ma sono proprio gli stessi valori?
piu( minmax(g, 1,3) ); piu(soluz(dg1,0, 1,3))
# 1.99999998773738 2
# Il secondo metodo è più preciso in quanto l'algoritmo per trovare il minimo e il
# massimo senza ricorrere alla derivate (pur essendo più generale) è più approssimativo
# (ma sono differenze che dal punto di vista applicativo sono in genere trascurabili).
#
# Per trovare E posso studiare dove cresce/decresce D(g)
maxmin(dg2,10,100)
# [1] 31.52936
# Oppure posso studiare dove si azzera la derivata 2^a
d2g2 <- function(x) eval( derivata2(g2,"x") )
soluz(d2g2,0, 10,100)
# [1] 31.52936
# Ho trovato lo stesso valore. In realtà i due procedimenti non danno gli stessi valori:
piu( maxmin(dg2,10,100) ); piu( soluz(d2g2,0, 10,100) )
# 31.5293616373527 31.5293611968877
# Anche in questo caso il secondo metodo dà un risultato più preciso.
# La y corrispondente è:
g( soluz(d2g2,0, 10,100) )
# [1] 0.9412041
# Dunque E = (31.52936, 0.9412041)
#
# Volendo potrei calcolare le derivate a mano, o con R. Con derivata(g2,"x") ho:
# ((x/4)^2)^((1/3)-1)*((1/3)*(2*(1/4*(x/4))))-(x-4)^((1/3)-1)*(1/3) che posso sempli-
# ficare in (x/4)^(-1/3)/6 - (x-4)^(-2/3)/3 ... o posso usare WolgramAlpha. Se
# metto: solve ( d/dx d/dx ((x/4)^2)^(1/3)-(x-4)^(1/3) ) = 0
# ottengo 31.52936119688764498693379…
#
# Ecco come è stato ottenuto il grafico con le soluzioni:
HF=2.7; BF=2.7*2
graficoF( g, -1,40, 1)
grafico ( g, 3,5, 1)
a = 0; b = 2; c = 4; d = 8; e = soluz(d2g2,0, 10,100)
PUNTO( c(a,b,c,d,e), g( c(a,b,c,d,e) ), "red")
# altro:
coltrat="red"; grigliaV(2); grigliaV(4); grigliaV(8)
scrivi(0,1.4,"A"); scrivi(2,2.1,"B"); scrivi(5.5,1,"C")
scrivi(8,0.2,"D"); scrivi(31.53,0.75,"E")
(l'esempio è tratto da "Complementi ed esercizi di Analisi Matematica" di Aldo Ghizzetti)
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Confronto di g con:
f = function(x) abs(x)^(2/3)
graficoF (g, -1e5,1e5, "black"); graficoF (f, -1e5,1e5, "brown")
dg1 <- function(x) eval( derivata(g1,"x") )
soluz(dg1,0, 1,3)
# [1] 2
dg2 <- function(x) eval( derivata(g2,"x") )
soluz(dg2,0, 5,10)
# [1] 8
# Ho ritrovato B e D. Ma sono proprio gli stessi valori?
piu( minmax(g, 1,3) ); piu(soluz(dg1,0, 1,3))
# 1.99999998773738 2
# Il secondo metodo è più preciso in quanto l'algoritmo per trovare il minimo e il
# massimo senza ricorrere alla derivate (pur essendo più generale) è più approssimativo
# (ma sono differenze che dal punto di vista applicativo sono in genere trascurabili).
#
# Per trovare E posso studiare dove cresce/decresce D(g)
maxmin(dg2,10,100)
# [1] 31.52936
# Oppure posso studiare dove si azzera la derivata 2^a
d2g2 <- function(x) eval( derivata2(g2,"x") )
soluz(d2g2,0, 10,100)
# [1] 31.52936
# Ho trovato lo stesso valore. In realtà i due procedimenti non danno gli stessi valori:
piu( maxmin(dg2,10,100) ); piu( soluz(d2g2,0, 10,100) )
# 31.5293616373527 31.5293611968877
# Anche in questo caso il secondo metodo dà un risultato più preciso.
# La y corrispondente è:
g( soluz(d2g2,0, 10,100) )
# [1] 0.9412041
# Dunque E = (31.52936, 0.9412041)
#
# Volendo potrei calcolare le derivate a mano, o con R. Con derivata(g2,"x") ho:
# ((x/4)^2)^((1/3)-1)*((1/3)*(2*(1/4*(x/4))))-(x-4)^((1/3)-1)*(1/3) che posso sempli-
# ficare in (x/4)^(-1/3)/6 - (x-4)^(-2/3)/3 ... o posso usare WolgramAlpha. Se
# metto: solve ( d/dx d/dx ((x/4)^2)^(1/3)-(x-4)^(1/3) ) = 0
# ottengo 31.52936119688764498693379…
#
# Ecco come è stato ottenuto il grafico con le soluzioni:
HF=2.7; BF=2.7*2
graficoF( g, -1,40, 1)
grafico ( g, 3,5, 1)
a = 0; b = 2; c = 4; d = 8; e = soluz(d2g2,0, 10,100)
PUNTO( c(a,b,c,d,e), g( c(a,b,c,d,e) ), "red")
# altro:
coltrat="red"; grigliaV(2); grigliaV(4); grigliaV(8)
scrivi(0,1.4,"A"); scrivi(2,2.1,"B"); scrivi(5.5,1,"C")
scrivi(8,0.2,"D"); scrivi(31.53,0.75,"E")
(l'esempio è tratto da "Complementi ed esercizi di Analisi Matematica" di Aldo Ghizzetti)
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Confronto di g con:
f = function(x) abs(x)^(2/3)
graficoF (g, -1e5,1e5, "black"); graficoF (f, -1e5,1e5, "brown")
 # Si vede che per x che tende a Inf e a -Inf entrambe le curve salgono oltre ogni
# limite e con la concavità verso il basso.
# Si vede che per x che tende a Inf e a -Inf entrambe le curve salgono oltre ogni
# limite e con la concavità verso il basso.