43 classi Distanza tratteggi fitti: 1%
1. Alcune situazioni problematiche. Introduzione alle proprieta` delle misure di probabilita`
Consideriamo alcune situazioni problematiche:
(A) Anno 1995. Un grande mobilificio del paese XX, rinnovando la gamma dei suoi prodotti, vuole adattare il "formato" di alcuni mobili (letti, poltroncine da scrivania, …) alle caratteristiche fisiche della popolazione attuale e, a tal fine, si avvale della consulenza della società statistica Sifanstat. Questa utilizza come dati le misure delle altezze dei maschi ventenni, classificate in intervalli ampi 1 cm, rilevate alle visite di leva nel 1950 e nel 1990; nel paese XX tutti i giovani vengono sottoposti alla visita di leva; le misure così rilevate sono gli unici dati antropometrici completi, su tutta la popolazione (maschile), di cui si può disporre per il paese XX. |
Per avere un'idea del tipo di studi che fa la Sifanstat consideriamo un problema semplice. I letti matrimoniali prodotti finora dal mobilificio sono (internamente) lunghi 190 cm, adatti alla sistemazione comoda (tenendo conto dello spazio per il cuscino e per la rimboccatura inferiore) di un uomo alto meno di 183 cm. Usando i dati sulle altezze citati, la Sinfanstat vuole valutare le probabilità che un potenziale cliente nato nel 1930 e uno nato nel 1970 trovino i letti matrimoniali troppo corti, cioè siano alti almeno 183 cm.
Sotto è riprodotta un'elaborazione di tali dati, registrati come file altxx50.stf e altxx90.stf.
| 1 |
Le frequenze originali erano espresse percentualmente e arrotondate ai decimi (ad es. per l'intervallo [171,172) nel 1950 la frequenza relativa era 4.8%). Poiché STAT richiede che come frequenze siano introdotti numeri interi, i dati, nei file altxx50.stf e altxx90.stf, sono stati riscritti in forma "per mille" (all'intervallo [171,172) si è associato, come frequenza, il numero 48). Si noti che come numero di dati il programma, in nessuno dei due casi, visualizza 1000; ciò è dovuto al fatto che le frequenze originali erano arrotondate.
43 classi Distanza tratteggi fitti: 1%
44 classi Distanza tratteggi fitti: 1%
Nota: gli intervalli hanno ampiezza unitaria, per cui frequenza e densità di frequenza coincidono.
In assenza di ulteriori informazioni, la Sifanstat assume che la probabilità di un dato intervallo di altezze coincida con la sua frequenza relativa. Per es. assume che la probabilità che un cliente nato nel 1930 (ventenne nel 1950) sia alto 171 cm (misura troncata agli interi, cioè altezza in [171,172)) coincida con la frequenza 4.8% di tale altezza.
Questa ipotesi presuppone, ad esempio, che i clienti non provengano da particolari regioni del paese: se nella regione AA i maschi adulti sono mediamente più alti rispetto all'intero paese, e se i clienti venissero tutti da AA, le valutazioni basate sui nostri dati sarebbero sballate. In altre parole, è come se si ipotizzasse che l'istogramma di distribuzione delle altezze dei clienti nati nel 1930 sia più o meno uguale all'istogramma relativo al totale dei maschi nati in XX in tale anno.
Dunque, se indico con H1 l'altezza troncata ai centimetri di un potenziale acquirente nato nel 1930, con h un particolare numero naturale e con Pr(H1=h) la probabilità che un potenziale acquirente nato nel 1930 sia alto (troncando agli interi) h cm, per la Sifanstat:
Pr(H1=h) = frequenza relativa dell'altezza h cm tra i ventenni nel 1950
Devo trovare Pr(H1=183 or H1=184 or H1=185 or …), dove "or", come nei linguaggi di programmazione, indica un "o" non esclusivo; essendo [183,184), [184,185), … intervalli disgiunti, avrei potuto usare anche un "o" esclusivo. Poiché la frequenza dell'unione di classi disgiunte è, ovviamente, uguale alla somma delle frequenze delle singole classi, posso dire che (proprietà additiva):
Pr(H1=183 or H1=184 or H1=185 or …) = Pr(H1=183) + Pr(H1=184) + Pr(H1=185) + …
Per determinare la probabilità cercata potrei sommare una ad una le frequenze in [183,184), [184,185), … leggendole da altxx50.stf. In alternativa posso, usando STAT, ricorrere ai percentili per trovare la probabilità con cui l'altezza cade in [0, 183):
98 % : 181.765
99 % : 183.765
 |
Il percentile di ordine 98 è 181.7…, cioè al 98% altezza<181.7… cm. Quello d'ordine 99 è 183.765, cioè al 99% altezza<183.7… cm. |
98.5 % : 182.618
98.7 % : 183.0195
98.65 % : 182.9162
Da queste ulteriori uscite deduco che altezza<183.000… cm con una probabilità compresa tra 98.65% e 98.7%. Posso concludere che Pr(altezza<183 cm)=Pr(H1<183) = 98.7% (valore arrotondato).
| 2 |
(B) Come posso calcolare Pr(H1>183) e Pr(H2>183)?
|
L'uso dei connettivi, come vedremo meglio in seguito, ha un ruolo importante nel calcolo delle probabilità. Soffermiamoci su di esso.
(1) Esegui in QBasic il programma TABVER.bas (è nella cartella Bas) e verifica se ottieni uscite simili a quelle riprodotte a fianco. (2) Comprendi il programma e cerca di modificarlo (usando opportunamente il menu Edit) in modo da ottenere anche la stampa della tabella di verità dei connettivi and e not. (3) Trova esempi tratti dal linguaggio comune in cui "e" e "o" siano usati con significati diversi rispetto a quelli dei corrispondenti connettivi dei linguaggi di programmazione. | vero = -1 falso = 0 A B A OR B -1 -1 -1 -1 0 -1 0 -1 -1 0 0 0 A B A XOR B -1 -1 0 -1 0 -1 0 -1 -1 0 0 0 |
Consideriamo un'altra situazione:
(B) Lancio un dado; voglio trovare la probabilità che esca un numero dispari. Rispetto alla situazione (A) non sono di fronte a una "popolazione" finita, ma potenzialmente infinita (fatto un lancio, ne possiamo fare un altro), per cui non posso conoscere completamente la distribuzione delle uscite. |
| 4 |
Indicata con U l'uscita di un lancio di un dado che si comporta in questo modo, posso supporre che:
(•) Pr(U=1) = Pr(U=2) = Pr(U=3) = … = Pr(U=6)
Posso assumere che: (••) Pr(U=1 or U=2 or … or U=6) = 1.
Infatti qualunque valore assegni a U, tra quelli che U può assumere, una delle 6 equazioni risulta vera; quindi ad ogni lancio U=1 or U=2 or … or U=6 risulta essere vera; perciò, qualunque numero di lanci si effettui, la frequenza relativa dell'evento indicato dalla formula U=1 or U=2 or … or U=6 è 1.
U=i and U=j per i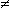
j è ovviamente falsa qualunque valore assuma U, cioè U=i e U=j (se i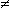j) sono eventi incompatibili.
È naturale estendere dal caso della popolazione finita (esempio (A)) a quello di una popolazione potenzialmente infinita la proprietà additiva, secondo cui la probabilità della disgiunzione (inclusiva) di più eventi incompatibili è pari alla somma delle probabilità di questi. Quindi, da (•) e (••), ho:
per ogni i in {1,2,3,4,5,6} si ha: Pr(U=i) = 1/6
Concludendo:
Pr(U
{1,3,5}) = Pr(U=1 or U=3 or U=5) = Pr(U=1) + Pr(U=3) + Pr(U=5) = 1/6 + 1/6 + 1/6 = 1/2
Se voglio determinare la probabilità che esca un numero pari, poiché "U è pari and U è dispari" è falsa qualunque sia il valore di U, "U è pari or U è dispari" è vera qualunque sia il valore di U, posso fare: Pr(U è pari) = Pr(U è pari or U è dispari) – Pr(U è dispari) = 1 – 1/2 = 1/2.
Consideriamo un'ulteriore situazione:
(C) Sta per disputarsi la partita Roma-Torino. Gigi ritiene che la Roma 30 su 100 vincerà e 40 su 100 pareggerà. Qual è la probabilità per Gigi che vinca il Torino?
Indico con E l'esito della partita, che potrà essere "1", "2" o "X", caratteri con cui indico, rispettivamente la vittoria, la sconfitta o il pareggio della squadra di casa.
E="1" or E="2" or E="X" è vera; E=a and E=b è falsa comunque prenda in {"1", "2", "X"} a e b diversi tra loro. Quindi, estendo anche a questa situazione la proprietà additiva:
Pr(E="2") = 1 – Pr(E="1" or E="X") = … = 1 – (30% + 40%) = 30%
È una situazione diversa dalle precedenti: non ho a che fare con una frequenza, anche se ci si esprime con il linguaggio "delle frequenze" ("30 su 100", …). Infatti Gigi valuta la probabilità di vittoria in base alle sua valutazioni sullo stato di forma delle due squadre, sulle condizioni di salute dei giocatori, … e in base alle sue speranze. Avrebbe senso ricorrere a una valutazione basata sulle frequenze solo se non si disponesse di informazioni sull'andamento del campionato, non ci si basasse sulle proprie aspettative, … e si avessero a disposizione i risultati degli incontri precedenti tra le due squadre.
Consideriamo un'ultima situazione:
(D) Delle bombe arrivano su una città e nei dintorni; all'interno della città le bombe arrivano distribuendosi praticamente in maniera uniforme sul territorio (cioè non privilegiando alcuna zona della città). Il territorio della città viene distinto in zone di tipo A (in cui sono presenti molti insediamenti industriali), di tipo B (densamente abitate), di tipo C (zone che sono sia di tipo A che di tipo B) e di tipo D (zone poco abitate e con pochi insediamenti industriali). Sapendo che la superficie totale della città è 89 km2, quella di A è 26 km2, quella di B è 43 km2,quella di C è 12 km2, si vuole stabilire le probabilità che una bomba che arriva in città cada in A, cada in B, cada in C e, infine, cada in D.
|
Indico con P il punto in cui cade la bomba. È naturale prendere: area di Z Pr(P Pr(P Pr(P Per calcolare Pr(P |
 |
Pr(PD) = Pr(not PA
B) = 1 – Pr(PAB) = 1 – (Pr(PA) + Pr(PB) – Pr(PC)) = 36%
| <<< Scheda precedente | INDICE | Paragrafo successivo >>> |