P).5. Suggerimenti e risposte ai quesiti
| 1 |
Per eseguire TestRnd.bas vedi i commenti al ques. 3 della scheda 2. Poi non uscire dal QBasic: lo userai nuovamente nel corso della scheda.
| 2 |
Indichiamo con U1 e U2 le variabili casuali che rappresentano le uscite dei due dadi, con P e con D gli insiemi dei numeri pari e dei numeri dispari. Dobbiamo determinare Pr(U1+U2P).
• U1+U2P equivale a (U1P and U2P) or (U1D and U2D)
Poiché P e D sono insiemi disgiunti, U1P and U2P e U1D and U2D sono eventi incompatibili; quindi, per la proprietà additiva:
Pr((U1P and U2P) or (U1D and U2D)) = Pr(U1P and U2P) + Pr(U1D and U2D)
Poiché U1 e U2 sono indipendenti, abbiamo:
Pr(U1P and U2P) = Pr(U1P) · Pr(U2P) e Pr(U1D and U2D) = Pr(U1D) · Pr(U2D)
Ma, per la proprietà additiva, essendo U1 e U2 dotate di distribuzione uniforme, abbiamo:
Pr(U1P) = Pr(U2P) = 1/6 + 1/6 + 1/6 = 1/2 e Pr(U1D) = Pr(U2D) = … = 1/2
Quindi:
Pr(U1+U2P) = Pr(U1P) · Pr(U2P) + Pr(U1D) · Pr(U2D) = 1/2·1/2 + 1/2·1/2 = 1/4 + 1/4 = 1/2
• Potevamo, invece che esplicitare gli usi della "regola della somma" e della "regola del prodotto", ricorrere alla costruzione di un grafo ad albero:
dopo aver osservato che Pr(U1P) = Pr(U2P) = Pr(U1D) = Pr(U2D) = 1/2 possiamo (1) rappresentare con successive diramazioni i diversi esiti possibili ("pari" e "dispari") per U1 e per U2, poi (2) associare ad ogni arco la corrispondete probabilità, quindi (3) calcolare per ogni nodo finale il prodotto dei valori associati agli archi che si percorrono per arrivare ad esso dal nodo iniziale (abbiamo usato la regola del prodotto); infine (4) (usando la regola della somma) sommiamo i valori dei nodi finali corrispondenti ai percorsi che individuano i casi "favorevoli":
• Si poteva anche procedere così: (U1,U2) ha distribuzione uniforme in {1,2, …,6}2 per cui posso calcolare il totale N delle coppie possibili e il totale M delle coppie che forniscono un'uscita pari e, infine, calcolare il rapporto N/M: infatti, essendo uniforme la distribuzione, la probabilità che esca una qualunque coppia è 1/M e, per la proprietà additiva, la probabilità che esca una delle N coppie che forniscono un'uscita pari è 1/M + 1/M + … = 1/M·N = N/M.
|
– le coppie possibili sono 6·6: 6 possibili valori di U1 e 6 possibili valori di U2 – le coppie "favorevoli" sono 6·3: 6 possibili valori di U1 e, per ciascuno di questi, 3 possibili valori di U2 (se U1 è pari U2 deve essere pari, …) Quindi la probabilità è: 6·3/(6·6) = 1/2. |
|
• Il lancio successivo dello stesso dado (equo) è un fenomeno del tutto analogo al precedente, in quanto i due lanci possono essere ritenuti indipendenti.
| 3 |
Indichiamo con A1, A2, A3 e A4 i quattro possibili stati della macchina.
Nei primi tre casi la macchina si mette in funzione in meno di 3 ore, nell'ultimo dopo 24 ore. Quindi dobbiamo calcolare Pr(A1 or A2 or A3).
Essendo eventi incompatibili, potremmo usare direttamente la proprietà additiva, ma, poiché si tratta di un gruppo completo di eventi, comporta meno calcoli procedere in questo modo:
Pr(A1 or A2 or A3) = 1 – Pr(A4) = 1 – 0.15 = 85%
| 4 |
Indichiamo con H e con K gli eventi che, rispettivamente, il dispositivo H e il dispositivo K continuino a funzionare. Dobbiamo trovare Pr(H or K). Possiamo procedere così:
Pr(H or K) = Pr((H and K) or (H and not K) or (not H and K)) =
Pr(H and K) + Pr(H and not K) + Pr(not H and K) =
0.8·0.7 + 0.8·0.3 + 0.2·0.7 = 0.94
oppure così:
|
Pr(H or K) = Pr(not(not H and not K)) = 1 – 0.2·0.3 = 0.94 oppure: … Usando un grafo, si poteva procedere nel modo illustrato a fianco: devo trovare la somma delle probabilità corrispondenti ai nodi finali dei percorsi che contengono almeno una "F" (almeno una macchina in funzione); questi sono 3; allora mi conviene calcolare la probabilità corrispondente al rimanente nodo finale, e poi farne la differenza da 1. |
 |
Alzata. Avendo supposto il mazzo nuovo (e non truccato e mescolato bene) possiamo supporre che, tagliandolo, le carte compaiano con distribuzione uniforme. Casi possibili: 40·40 (40 carte possibili per la prima alzata e 40 per la seconda); casi favorevoli: 40·20 (sono 20 le carte dello stesso colore di quella ottenuta con la prima alzata); probabilità: 20/40=1/2.
Ovvero, riferendosi direttamente al colore, cioè considerando come sistema completo di eventi incompatibili i due eventi "la carta è rossa" e "la carta è nera": casi possibili: 2·2, casi favorevoli: 2·1; probabilità: 1/2. |
  |
|
Estrazione. Casi possibili: 40·39 (alla seconda estrazione dispongo di una carta in meno); casi favorevoli: 40·19 (sono 19 le carte rimaste nel mazzo dello stesso colore di quella ottenuta con la prima estrazione). Probabilità: 19/39. |  |
| 6 |
Alla prima domanda la risposta sembra facile: le uscite possibili minori o uguali a 3 sono una pari e due dispari, per cui se l'uscita U è minore o uguale a 3 è più probabile che essa sia dispari. I due eventi non sembrano essere indipendenti. Verifichiamolo mediante la definizione:
Pr(U è pari and U≤3) = Pr(U=2) = 1/6; Pr(U è pari)·Pr(U≤3) = 3/6·3/6 = 1/4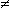 
1/6.
Anche nel secondo caso si può essere inclini a ritenere che gli eventi non siano indipendenti: se l'uscita U è minore o uguale a 3 è più probabile che essa sia 1 piuttosto che essere 4, poiché questa seconda eventualità ha probabilità 0. Facciamo i conti:
Pr(U{1,4} and U≤3) = Pr(U=1) = 1/6, Pr(U{1,4})·Pr(U≤3) = 2/6·3/6 = 1/6.
Quindi gli eventi sono, invece, indipendenti. Che cos'è all'origine dell'"intuizione" sbagliata? Nel ragionamento avevamo interpretato la domanda come se si richiedesse di valutare l'indipendenza di U≤3 dall'evento U=1 e dall'evento U=4 piuttosto che dall'evento "U=1 or U=4".
| 7 |
Si deve determinare Pr(malato|positivo), cioè la probabilità che, essendo positivi, si sia anche malati: Pr(A|B) indica la probabilità che, nella "condizione" in cui accade l'evento B, accada anche l'evento A. In altre parole dobbiamo determinare Pr(malato and positivo)/Pr(positivo): l'universo a cui riferire l'essere malato non è più il totale della popolazione, ma il sottoinsieme dei positivi; vedi la fig. seguente.
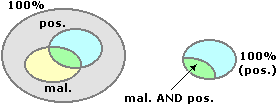
Per calcolare questo rapporto dobbiamo trovare il valore dei "?" della tabella seguente. Per completare la tabella mettiamo i dati sulla popolazione (prime due colonne dell'ultima riga), poi utilizziamo il dato sull'attendibilità del test (per ottenere le prime due colonne della prima riga: 1·95%=0.95, 99·5%=4.95), infine elaboriamo la tabella (ci basta completare la prima riga: 0.95+4.95=5.90).
|
 |
|
|
|
La probabilità cercata è dunque 0.95%/5.90% = 16%, cioè molto meno del 95%, come in prima battuta qualcuno potrebbe rispondere.
|
Se si risultasse positivi anche a una seconda effettuazione del test (supponendo questa indipendente dalla prima), la probabilità di essere malati sarebbe molto maggiore: |
Trasformando i dati in forma percentuale posso valutare meglio l'esistenza di "proporzionalità". Concludo immediatamamente che le variabili "sesso" (a uscite: M, F) e "settore" (a uscite: agr., ind., altro) non sono indipendenti: le righe dei dati non sono più o meno proporzionali (ovvero le righe delle percentuali non sono più o meno uguali). Posso invece ritenere indipendenti "sesso" (degli occupati) e "occupazione in agricoltura" (a uscite: sì, no): 1ª e 4ª riga sono "quasi" proporzionali. |
M F
agricoltura 64% 36%
industria 76% 24%
altre attiv. 60% 40%
totale 65% 35%
|
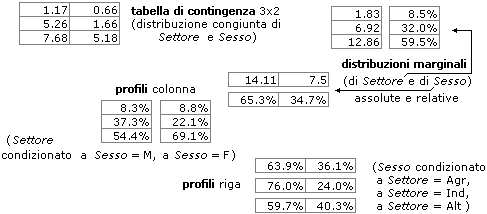
A volte, nella manipolazione delle tabelle di contingenza, si usano alcune terminologie specifiche (distribuzioni marginali, profili riga e colonna), richiamiate (attraverso una esemplificazione) nelle figure sottostanti, che illustrano anche come un foglio di calcolo elettronico può essere utile per rappresentare (percentualmente e graficamente) ed elaborare tabelle di dati (i dati sono stati scritti nel "rettangolo" B2-C4, le elaborazioni numeriche sono state ottenute con le 4 "formule" sotto riprodotte, che sono state "estese" verticalmente od orizzontalmente alle altre celle, con una modifica automatica dei "riferimenti" ai dati da elaborare; l'istogramma rappresenta sia la distribuzione di Settore che le tre distribuzioni condizionate di Sesso).
| 9 |
(1) Evidentemente è più probabile perdere la scommessa che vincerla. Tuttavia se il signor X non scommette ha probabilità nulla di poter acquistare il biglietto (a meno che non trovi qualche altra soluzione), mentre se scommette può sperare di poterlo acquistare.
(2) La conclusione non è corretta perché anche il tipo di alimentazione si "trasmette" familiarmente. Molte ricerche sull'ereditarietà (genetica) dell'intelligenza, di malattie psichiche, … sono state basate su indagini statistiche e analisi in cui si sono confuse dipendenza probabilistica e dipendenza funzionale.
| 10 |
Utilizziamo la variabile casuale N a valori in {0,1,2,…,10} per rappresentare il numero di teste uscite in 10 lanci. Dobbiamo calcolare Pr(N>5).
Poiché la moneta è equa, Pr(N<5) = Pr(N>5). Quindi Pr(N>5) = (1 - Pr(N=5))/2.
Dobbiamo, dunque, calcolare Pr(N=5).
|
Poiché i lanci sono indipendenti, per la regola del prodotto la probabilità che testa esca nei primi 5 lanci è (1/2)10, cioè 2–10. |
 |
La stessa probabilità vale per qualsiasi altra disposizione dei 5 posti. I modi in cui posso scegliere i 5 posti sono C(10,5), dove con C(n,k) si indicano le combinazioni di n elementi k a k, cioè la quantità dei sottoinsiemi di cardinalità k di un insieme di cardinalità n.
Quindi, la probabilità cercata, per la propietà additiva (regola della somma), è C(10,5)/210.
Come calcolare C(n,k)?
• Come posso prendere k elementi? Per il primo ho n possibilità, per il secondo n–1, … . In definitiva ho n·(n–1)·(n–2)·…·(n–k+1) (con k fattori moltiplicativi) possibilità.
[è la quantità di sequenze di lunghezza k realizzabili con n oggetti; queste sequenze vengono dette anche "disposizioni di n elementi k a k"]
• Non importa l'ordine con cui scelgo i k elementi (la successione x,y,z – x 1° elemento, y 2° e z 3° – ha gli stessi elementi delle successioni x,z,y e y,x,z e …). Quindi devo dividere n·(n–1)·(n–2)·…·(n–k+1) per la quantità dei modi in cui posso ordinare k elementi.
• Con un ragionamento analogo al precedente ho che questa quantità è k·(k–1)· …·2·1 = k! (fattoriale di k).
[i modi in cui posso disporre in ordine k elementi o, meglio, le sequenze di k elementi realizzabili con k oggetti vengono dette anche "permutazioni di k elementi"]
• Quindi:
n·(n-1)·(n-2)·…·(n-k+1) C(n,k) = —————————————————————— k!
Tornando al nostro problema:
Pr(N=5) = C(10,5)·2-10 = 10/5·9/4·8/3·7/2·6/1·2-10 = 9·4·7·2-10 = 24.6%,
quindi:
Pr(N>5) = (1– 24.6%)/2 = 37.7%.
10
Nota. Σ Pr(N=i) deve valere 1 (100%). Ciò accade, infatti:
i=0ΣC(10,i) = (quantità dei sottoinsiemi di cardinalità 0 di un insieme di cardinalità 10) + (quantità dei sottoinsiemi di cardinalità 1 di un …) + … + (quantità dei sottoinsiemi di cardinalità 10 di un …) = (quantità dei sottoinsiemi di un insieme di cardinalità 10) = (quantità delle funzioni da un insieme di cardinalità 10 in {0,1}) = 210. Quindi 
§4) è stato definito Pr(N=x) usando il menu CALC e il sottomenu SOMMA, si può calcolare la somma G(0)+G(1)+…+G(10).
| <<< Paragrafo precedente | INDICE | Scheda successiva >>> |