Risolvi il quesito 10 della scheda 3 usando Poligon (e le definizioni di P e G sotto richiamate)
sia con il calcolo di Pr(N=6)+…+Pr(N=10),
sia con il calcolo dell'area sotto al grafico della funzione G in un opportuno intervallo.
Confronta i due valori ottenuti.
P(x) = !(#n)/(!(#n-x)*!(x))/2^#n
G(x) = 1/(SQR(2*PI)*#s)*EXP(-(x-#m)^2/(2*#s^2))
Il concetto di funzione di densità è stato messo a punto per poter svolgere nel caso di una variabile casuale a valori in un intervallo di numeri reali considerazioni analoghe a quelle che, nel caso di una variabile casuale discreta, vengono riferite all'istogramma (o alla poligonale) della legge di distribuzione.
Nel caso discreto (con valori possibili v1, v2, …) quando l'istogramma sperimentale (rettangoli con altezze FreqRel(vi)) all'aumentare del numero delle prove tende a stabilizzarsi, si assume come modello matematico del comportamento del fenomeno (rappresentato con la variabile casuale U) una misura di probabilità Pr tale che l'istogramma con rettangoli di altezze Pr(U=vi) sia assumibile come "limite" dell'istogramma sperimentale.
Nel caso in cui U ha valori che possono cadere in tutto un intervallo I di estremi a e b (finiti o infiniti), l'istogramma sperimentale dipende dall'ampiezza h dei sottointervalli di I in cui vengono classificati i dati, e, affinché all'aumentare del numero delle prove e al diminuire dell'ampiezza h dei sottointervalli si possa individuare una eventuale forma su cui la parte superiore dell'istogramma (ovvero la poligonale di distribuzione) tenda a stabilizzarsi, come altezze dei rettangoli dobbiamo prendere non FreqRel(sottointervallo i-esimo), ma FreqRel(sottointervallo i-esimo)/h, cioè le frequenze relative unitarie, o densità di frequenza (vedi scheda 1, §5). L'eventuale curva su cui tendono a stabilizzarsi i contorni degli istogrammi sperimentali sarà una curva che delimiterà, assieme all'asse x, una superficie con area 1.
Se rappresento questa curva come il grafico di una funzione f con dominio I, se f è integrabile su I posso porre, per ogni c e d in I, Pr(c≤U≤d) = c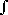 d f. Questa funzione, quindi, è una caratterizzazione della legge di distribuzione di U, e viene chiamata densità di probabilità [della legge di distribuzione] di U. d f. Questa funzione, quindi, è una caratterizzazione della legge di distribuzione di U, e viene chiamata densità di probabilità [della legge di distribuzione] di U.
|
Abbiamo già visto due esempi di funzioni di densità nella scheda 1.
Uno era la densità di probabilità della legge di distribuzione delle durate delle telefonate; si trattava [ figura a lato] di una densità normale. Osserviamo che, ad essere rigorosi, il numero delle telefonate (a parità di condizioni) non può tendere all'infinito; ha senso considerare il grafico della funzione di densità come "limite" dell'istogramma sperimentale solo se idealizziamo la situazione. figura a lato] di una densità normale. Osserviamo che, ad essere rigorosi, il numero delle telefonate (a parità di condizioni) non può tendere all'infinito; ha senso considerare il grafico della funzione di densità come "limite" dell'istogramma sperimentale solo se idealizziamo la situazione. |
 |
|
L'altro esempio era la densità di probabilità della legge di distribuzione dei tempi intercorsi tra una telefonata e la successiva [ figura a lato] (densità esponenziale). figura a lato] (densità esponenziale). |  |

|
Nel quesito 8 della scheda 2 abbiamo studiato RND e abbiamo osservato
(vedi figura sopra a sinistra) che, in base all'esito delle sperimentazioni effettuate, si può
ritenere che abbia legge di distribuzione uniforme in [0,1).
Se esportiamo in Poligon gli istogrammi sperimentali (in scala normalizzata, cioè con le altezze dei rettangoli
che rappresentano le densità di frequenza),
otteniamo che il contorno dell'istogramma tende a disporsi lungo il grafico della funzione
x  1. Questa, per x in [0,1), è la funzione
ensità di RND (se, idealizzando, supponiamo che RND possa assumere come valore tutti i numeri
reali tra 0 e 1). 1. Questa, per x in [0,1), è la funzione
ensità di RND (se, idealizzando, supponiamo che RND possa assumere come valore tutti i numeri
reali tra 0 e 1).
Una variabile casuale U a valori in un intervallo di estremi a e b per cui esista una funzione di densità f viene detta variabile casuale continua.
In tal caso si possono definire la media M(U) di U e il suo scarto quadratico medio σ(U) in analogia al caso discreto:
Consideriamo le variabili casuali continue finora introdotte:
• Distribuzione uniforme in [0,1) (f(x) = 1):
m = 0 1 x·f(x) dx = 0 1 x·f(x) dx = 0 1 x dx = [x2/2]x=1 - [x2/2]x=0 = 1/2 1 x dx = [x2/2]x=1 - [x2/2]x=0 = 1/2
[ovvero, senza usare l'integraz. indefinita: 0 1 x dx = area del triangolo (0,0)-(1,0)-(1,1) = 1/2] 1 x dx = area del triangolo (0,0)-(1,0)-(1,1) = 1/2]
σ = 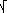 ( 0 ( 0 1(x - m)2 f(x) dx ) = 1(x - m)2 f(x) dx ) = 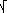 ( 0 ( 0 1(x - 1/2)2 dx ) = 1/ 1(x - 1/2)2 dx ) = 1/  12
[senza usare l'integrazione indefinita, con POLIGON potrei fare: 12
[senza usare l'integrazione indefinita, con POLIGON potrei fare:
f(x)=1
g(x)=(x-1/2)^2*f(x)
[0,1] g INT = 0.08333333333333333 = 1/12]
Sperimentalmente, per RND, si era trovato come s.q.m. statistico (con 1000 prove) 0.2855 (vedi scheda 2, ques.8), vicino a 1/ 12= 0.2887. 12= 0.2887.
• Distribuzione uniforme in [a,b):
la densità è f(x)=1/(b-a), la media è (a+b)/2, lo s.q.m. è (b–a)/  12. 12.
• Distribuzione esponenziale (f(x)= ae–ax):
Anche sperimentalmente si erano trovati media e s.q.m. molto vicini tra loto (vedi scheda 1, ques.9).
• Distribuzione gaussiana "di media 0 e scarto quadratico medio 1" [vedi §1]; ottengo (a conferma della dizione "di media 0 e s.q.m. 1"):
| f(x) = |  | (- <x< <x< ) ) | media = |  | x f(x) dx = 0 | s.q.m. = 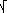 ( ( |  | x2f(x) dx ) = 1 |
[anche in questo caso con Poligon posso ritrovare questi valori]
Se considero la gaussiana "di media m", cioè g(x)=f(x–m), ottengo, per la media, l'equivalenza (poiché "traslando orizzontalmente" l'integrale tra – e e  non muta) con l'integrale di (x+m)f(x), cioè con la differenza tra l'integrale di xf(x) e l'integrale di mf(x), che vale 0+m·1, cioè proprio m. Per lo s.q.m. ottengo ancora 1. non muta) con l'integrale di (x+m)f(x), cioè con la differenza tra l'integrale di xf(x) e l'integrale di mf(x), che vale 0+m·1, cioè proprio m. Per lo s.q.m. ottengo ancora 1.
Se considero la densità gaussiana h "di s.q.m. σ", osservo che h(x)=f(x/σ)/σ per cui ottengo, per lo s.q.m., l'integrale di x2f(x/σ)/σ che equivale ("contraendo orizzontalmente" e "dilatando verticalmente" in modo reciproco) all'integrale di σ(x·σ)2f(x)/σ, cioè di σ2x2f(x), che vale σ2·1, la cui radice è, appunto, σ. Quindi:
• la distribuzione gaussiana "di media m e s.q.m. σ" ha effettivamente m e σ come media e s.q.m..
|

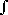 d f. Questa funzione, quindi, è una caratterizzazione della legge di distribuzione di U, e viene chiamata densità di probabilità [della legge di distribuzione] di U.
d f. Questa funzione, quindi, è una caratterizzazione della legge di distribuzione di U, e viene chiamata densità di probabilità [della legge di distribuzione] di U. figura a lato] di una densità normale. Osserviamo che, ad essere rigorosi, il numero delle telefonate (a parità di condizioni) non può tendere all'infinito; ha senso considerare il grafico della funzione di densità come "limite" dell'istogramma sperimentale solo se idealizziamo la situazione.
figura a lato] di una densità normale. Osserviamo che, ad essere rigorosi, il numero delle telefonate (a parità di condizioni) non può tendere all'infinito; ha senso considerare il grafico della funzione di densità come "limite" dell'istogramma sperimentale solo se idealizziamo la situazione.


 1.
1. Σxi·f(xi)
Σxi·f(xi)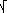
 b (x-M(U))2·f(x) dx
b (x-M(U))2·f(x) dx 
 12
12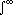 x·f(x) dx = 0
x·f(x) dx = 0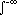 ueu du = 1/a
ueu du = 1/a
 <x<
<x<