0. Introduzione alla seconda parte (schede 5-8).
In questa seconda parte del corso (schede 5-8) approfondiamo alcuni dei concetti introdotti nella prima parte e sviluppiamo i collegamenti tra probabilità e statistica. Gli argomenti non sono affrontati in modo esauriente (alcuni sviluppi tecnici richiederebbero, altrimenti, molto più spazio e molto più tempo), ma, riteniamo, in modo sufficiente per avere un'idea relativamente chiara dei principali aspetti della Teoria della Probabilità e per inquadrare sia gli argomenti relativi a quest'area matematica previsti per i vari indirizzi del triennio della scuola secondaria superiore, sia i possibili collegamenti con altre materie (afferenti alle scienze sperimentali e all'informatica).
1. M(U1+U2), M(kU), M(U1*U2); la VARIANZA; Var(U1+U2), Var(kU). Considerazioni teoriche e studio sperimentale. Applicazioni al caso della legge BINOMIALE. Come effettua i calcoli una CT.
Perché è frequente l'impiego della distribuzione gaussiana?
Vi sono molti fenomeni che si comportano in modo "gaussiano". Cerchiamo di dare una spiegazione razionale a questo fatto.
Abbiamo già visto, sperimentalmente, che la legge binomiale di ordine n (Pr(N=i) = C(n,i)/2n) per n sufficientemente grande è ben approssimata dalla legge gaussiana (con medesimi media e s.q.m.: vedi scheda 4, §1 - §2).
La legge binomiale è rappresentabile anche come somma di n variabili casuali Xi con la stessa distribuzione di X=INT(RND*2), cioè con distribuzione uniforme in {0,1}: vedi scheda 3, § 4.
Ora proviamo a sommare variabili casuali con distribuzione uniforme in [0,1).
| 1 |
A priori, che cosa possiamo dire di M(ΣXi)? Cioè, qual è la media teorica di ΣXi?
Affrontiamo una situazione più semplice.
Consideriamo il lancio di due dadi (U=U1+U2). Qual è la media?
Abbiamo visto che M(U1+U2)=7 (
analisi del file DADITEO, scheda2,§6). Che relazione ha con le medie di U1 e di U2?
M(U1)=M(U2)="media pesata dei valori"=1·1/6+2·1/6+… + 6·1/6 = (1+2+…+6)/6 = 7·6/2/6 = 3.5
Quindi, in questo caso, M(U1+U2)=M(U1)+M(U2).
Verifichiamo se vale una relazione analoga anche nel caso dei 10 lanci di una moneta equa. Si tratta della somma di 10 variabili discrete X1, …, X10 con distribuzione uniforme in {0,1}.
Abbiamo già osservato che ( analisi del file MONETEO, scheda3,§4) che M(X1 + … + X10) = 5.
M(X1) = … = M(X10) = 0·1/2 + 1·1/2 = 1/2.
Quindi anche in questo caso M(X1 + … + X10) = M(X1) + … + M(X10)
In generale, se U1 e U2 sono due variabili aleatorie dotate di media, si ha:
M(U1+U2) = M(U1) + M(U2) [e di conseguenza M(U1+U2+…) = M(U1)+M(U2)+…]
Vediamone la dimostrazione per il caso in cui U1 e U2 sono variabili casuali discrete e finite; passando agli integrali si ottiene quella per il caso continuo. Sia U=U1+U2; siano ai, bj, vk i valori che possono assumere, rispettivamente, U1, U2 e U; i vk sono, quindi, i valori che possono assumere le somme ai+bj.
|
|
M(U) = Σkvk·Pr(U=vk) = Σkvk·Pr(U1+U2=vk) = ΣiΣj(ai+bj)·Pr(U1=ai and U2=bj) = ΣiΣjai·Pr(U1=ai and U2=bj) + ΣiΣjbj·Pr(U1=ai and U2=bj) = Σiai·ΣjPr(U1=ai and U2=bj) + Σjbj·ΣiPr(U1=ai and U2=bj) = Σiai·Pr(U1=ai) + Σjbj·Pr(U2=bj) = M(U1)+M(U2) |
Per comprendere il terzo passaggio (Σk … = ΣiΣj…) si pensi al caso dei due dadi: dalla sommatoria (vedi la tabella rappresentata) diagonale per diagonale si passa alla sommatoria casella per casella). Per comprendere il penultimo passaggio si noti che ΣjPr(U1=ai and U2=bj) = Pr(U1=ai) deriva dal fato che gli U2=bj sono eventi tra loro incompatibili la cui unione è un evento certo. Analogamente ΣiPr(U1=ai and U2=bj) = Pr(U2=bj).
È immediato dimostrare che, se k è una costante e U è dotata di media:
M(kU)=kM(U) (per k intero positivo è anche un corollario della prop. precedente).
Si usa, implicitamente, questa proprietà ad esempio per ricondurre la media di 12.3, 17.5, 0.7 alla divisione per 10 di quella di 123, 175, 7 e tutte le volte che si operano dei cambi di unità di misura sui dati da analizzare.
Tornando al caso del quesito 1, M(Xi) = 1/2; quindi M(ΣiXi) = Σi(1/2) = 1/2·20 = 10, in accordo con l'esito sperimentale (9.959…).
Poniamoci il problema analogo al precedente per il prodotto delle uscite (U=U1·U2).
Nel caso delle nostre Ui (lancio di due dadi) abbiamo già trovato che M(U1·U2) = 12.25 ( scheda2, §7), che è uguale a M(U1)·M(U2) = 3.5·3.5. Ma se U1 e U2 sono, ad es., il valore sulla faccia superiore e il valore sulla faccia inferiore ottenuti lanciando un solo dado equo, poiché la somma dei punti su facce opposte è 7, si ha: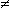 
In generale: M(U1·U2) = M(U1)·M(U2) se U1 e U2 (sono dotate di media e) sono indipendenti
Vediamone la dimostrazione per il caso finito (con le notazioni impiegate per la dimostrazione precedente):
M(U) = Σkvk·Pr(U=vk) = Σkvk·Pr(U1·U2=vk) =
Il quarto passaggio è giustificato dall'indipendenza di U1 e U2.
Nota 1. La formula M(U1+U2) = M(U1)+M(U2) vale anche se U1 e U2 sono dipendenti.
Quindi, ad esempio, la media di X, numero di carte di cuori che ottengo estraendo 5 carte da un mazzo (cioè X=X1+…+X5 dove Xi è 1 se all'i-esima estrazione esce cuori, 0 altrimenti), anche se l'esito di ogni estrazione condiziona l'esito della successiva, è M(ΣXi) = ΣM(Xi) = 5·1/4 = 1.25, come nel caso in cui procedessi con 5 "alzate".
Infatti "a priori", se non conosco l'esito della 1a estrazione, anche per la 2a estrazione devo assumere 1/4 come probabilità che esca cuori, e così via per le successive.
Tornando nuovamente al quesito 1, ci poniamo il problema di come determinare teoricamente σ(ΣXi).
È più comodo fare i calcoli senza radice quadrata, cioè considerare σ(U)2 (che si scriverebbe σ2(U), usando le notazioni in genere impiegate in analisi), che viene chiamata varianza di U e indicata con Var(U) o con V(U) (da alcuni, con D(U)):
Var(U) = σ(U)2 = M((U–M(U))2)
[media dei quadrati degli scarti dalla media]
Si ha:
Var(U1+U2) = Var(U1) + Var(U2) se U1 e U2 sono indipendenti (e dotate di media e varianza)
Infatti: Var(U1+U2) = M( ((U1+U2)–M(U1+U2))2 ) = M( ((U1–M(U1))+(U2–M(U2)))2 ) =
M( (U1–M(U1))2+(U2–M(U2))2 – 2·(U1–M(U1))·(U2–M(U2)) ) =
M( (U1–M(U1))2 ) + M( (U2–M(U2))2 ) – 2·M( (U1–M(U1))·(U2–M(U2)) ) =
Var(U1) + Var(U2) – 2 M(U1–M(U1)) · M(U2–M(U2)) = Var(U1) + Var(U2)
Il penultimo passaggio è giustificato perché U1 e U2 sono indipendenti. L'ultimo passaggio segue dal fatto che, per ogni variabile casuale U, M(U–M(U)) = M(U)–M(U) = 0.
Questa dimostrazione e le precedenti sono relativamente facili da comprendere nei vari passaggi ma, al livello della scuola secondaria superiore, non è certo il caso di affrontarle in classe. Può esserne eventualmente dimostrata la versione statistico-descrittiva (più facile). È invece utile verificarle con esempi e controesempi (capendo perché in questi secondi casi non valgono), anche mediante il calcolatore. Controlliamo, ad es., la validità della prima e dell'ultima proprietà nel caso del lancio di due dadi equi (per trovare la varianza si potrebbe anche usare Stat, applicato a DadiTeo.stf - scheda 2, §6 - o a file simili).
| 2 |
M(U1)=M(U2) = 3.5
V(U1)=V(U2) = 2.916667 V(U1)+V(U2) = 5.833333
M(U1+U2) = 7
V(U1+U2) = 5.833333
' Verifica di M(U1+U2)=M(U1)+M(U2) e Var(U1+U2)=Var(U1)+Var(U2)
' per il lancio di due dadi equi
PRINT
DIM x(6),y(6),xy(36),q(36)
FOR i=1 TO 6: x(i)=i: y(i)=i: NEXT 'metto in x(),y() le possibili uscite di U1,U2
MEDIA x(),6,m: PRINT "M(U1)=M(U2) ="; m
FOR i=1 TO 6: q(i)=(x(i)-m)^2: NEXT ' metto in q() i quadrati degli scarti
MEDIA q(),6,var: PRINT "V(U1)=V(U2) ="; var; " V(U1)+V(U2) ="; var+var
i=0
FOR j=1 TO 6: FOR k=1 TO 6
i=i+1: xy(i)=x(j)+y(k)
NEXT: NEXT ' metto in xy() le somme delle possibili uscite di (U1,U2)
MEDIA xy(),36,mm: PRINT "M(U1+U2) =";mm
FOR i=1 TO 36: q(i)=(xy(i)-mm)^2: NEXT
MEDIA q(),36,var
PRINT "V(U1+U2)="; var
SUB MEDIA(x(),n,m) STATIC
s=0: FOR i=1 TO n: s=s+x(i): NEXT
m=s/n
END SUB
A proposito del sottoprogramma MEDIA, osserviamo che si tratta di un sottoprogramma di tipo
Sub-End Sub, che corrisponde, grosso modo, alle "procedure" di altri linguaggi. Si noti che
x(), n, m sono parametri formali: nella "chiamata" possono essere sostituiti con altri termini [x()
con un'altra variabile indiciata, n con un qualunque termine a valore numerico,
m, in cui viene messo il risultato, con un'altra variabile numerica].
Le variabili s e i presenti nel sottoprogramma (ossia le
variabili che non sono parametri formali) sono variabili locali: ad esse vengono associati registri diversi da quelli di
eventuali variabili con lo stesso nome che comparissero nel programma principale o in altri sottoprogrammi; quindi la i
non dà luogo a "conflitti" con altri usi di essa nel programma principale.
Nell'usuale linguaggio matematico sono "variabili locali" gli indici impiegati nelle sommatorie o le variabili associate a "lim" o a "d" nella notazione per indicare un limite o un integrale definito:
| ( | lim 1/x | ) · x, ( | lim 1/u | ) · x e 0 · x sono equivalenti |
| x → ∞ | u → ∞ |
Sottoprogrammi e programma principale sono visualizzati in finestre diverse accessibili dal menu View. Per affrofondimenti sui sottoprogrammi si può vedere la voce calcolatore (5) degli Oggetti Matematici.
Applichiamo l'ultima proprietà al caso del quesito 1. Se Xi ha distribuzione uniforme in [0,1), V(Xi) = 1/12 ( scheda4,§2); quindi V(ΣXi) = ΣV(Xi) = 20·1/12 = 5/3, da cui σ(ΣXi) = 
(5/3)
Nel caso della legge binomiale (simmetrica) abbiamo già potuto osservare su più esempi (n=10, n=50) che, se Bn è una variabile casuale con distribuzione binomiale di ordine n, M(Bn)=n/2.
È facile dimostrarlo in generale. Sottintendiamo che nelle sommatorie l'indice i vari da 1 a n. Bn = ΣXi con Xi a distribuzione uniforme in {0,1} ( scheda3, §4); M(Xi)=1/2·0+1/2·1=1/2; M(ΣXi)= n·1/2=n/2.
Per la varianza: Var(Xi) = 1/2·(0–1/2)2 + 1/2·(1–1/2)2 = 1/4; Var(ΣXi)=n·1/4=n/4.
Quindi σ(Bn)= n / 2. Ad esempio per n=50 ritroviamo il valore 3.535… già trovato con STAT ( scheda3, §4).
| 3 |
[perché per k intero positivo sarebbe errato fare così: V(kU) = V(U+…+U) = V(U)+…+V(U) =
Nota 2. Come fa a calcolare la varianza una CT con tasti statistici? Non può usare la definizione perché la CT non memorizza i dati man mano introdotti. Ad es. per calcolare la media memorizza in due registri il numero N dei dati battuti e la loro somma S (richiamabili coi tasti 
e 
o analoghi); poi, se si batte il tasto "media", calcola e visualizza il risultato di S/N.
Procede invece utilizzando la trasformazione: Var(U) = M((U–M(U)2) = …
=
Infatti memorizza in un ulteriore registro la somma S2 dei quadrati dei dati (richiamabile con 
o tasto simile) e, se si batte il tasto "σ", visualizza il valore di (S2/N
Questa formula può essere, a volte, utile anche nel calcolo manuale. Ha, però, il difetto, se M(U2) e
Nota 3. Nel calcolo manuale spesso è utile ricorrere alle proprietà M(U) = k+M(U–k) e Var(U) =
media(105, 98, 103) = 100 + media(5,–2,3) = 100 + 6/3 = 102;
var(105,98,103) = var((5,–2,3) = …
| <<< Scheda precedente | INDICE | Paragrafo successivo >>> |