>>>>>
Scheda 5 - I teoremi limite
2. Il TEOREMA LIMITE CENTRALE. Abusi della distribuzione NORMALE.
A questo punto abbiamo gli strumenti per affrontare la questione che ci siamo posti all'inizio del primo paragrafo. Possiamo infatti enunciare il teorema (in cui scrivendo Σi sottintendiamo che la sommatoria è estesa da 1 a n):
|
Teorema limite centrale (debole).
Siano Ui (i intero positivo) variabili casuali (numeriche) indipendenti con la stessa legge di
distribuzione e M(Ui) = m, V(Ui) = σ2.
Allora la variabile casuale Xn = Σi Ui (che ha media m·n e varianza σ2·n, per le proprietà viste in §1) per n  tende ad avere legge di distribuzione normale.
Cioè, se Yn è una variabile distribuita normalmente con stesse medie e varianza di Σi Ui, per ogni h>0:
Pr(x ≤ Σi Ui < x+h) – Pr(x ≤ Yn < x+h) 0 per n
uniformemente rispetto a x | |
Quindi Xn/n tende alla normale Y' avente m e σ2/n come media e varianza
(infatti, per le proprietà viste in §1, M(U/k) = M(U)/k, Var(U/k) = Var(U)/k2):
Pr(x ≤ Σi Ui/n < x+h) Pr(x ≤ Y'n < x+h)
Il teorema limite centrale traduce "in formule" il fatto che l'istogramma di distribuzione (se le Ui sono discrete) o il grafico della funzione densità (se le Ui sono continue) di Xn [di Xn/n] e quello della funzione di densità di Yn [di Y'n] tendono a confondersi. |
 |
Nota. Se identifico una variabile discreta U a valori in {v1,
v2, …} con la variabile U* a valori in R tale che
Pr(U*=vi)=Pr(U=vi) e
Pr(U*=x)=0 se x
{v1, v2,
…} posso estendere ad essa il concetto di funzione di ripartizione.
Allora, nelle ipotesi del teorema limite centrale, posso considerare in ogni caso, anche in quello discreto, la funzione di
ripartizione Fn di Xn/n (Fn(x) =
Pr(Xn/n < x)) e, indicata con F la funzione di ripartizione gaussiana di media m
e varianza σ2/n, concludere che: Fn F (uniformemente). Questo è un modo in cui, spesso, viene presentato il teorema limite centrale.
|
Vale anche una versione forte del teorema limite centrale, secondo la quale la Xn tende ad avere una legge di distribuzione normale anche se le Ui non hanno la stessa legge, a patto che soddisfino una particolare condizione (detta "di Lindeberg") che, non rigorosamente, si può descrivere così: le Ui siano tali che, al crescere di n, ciascuna abbia un effetto trascurabile su Xn.
Il file a lato (registrato come LimCentr.bas) può essere utilizzato come sottoprogramma Prova da inserire in Fa_Rnd.bas per studiare la somma di 24 variabili casuali ( scheda 2). Con questo e con file analoghi si può verificare sperimentalmente in più casi particolari la validità del teorema "forte".
Per una rappresentazione animata di questa simulazione clicca QUI.
| |
u=0
FOR j=1 TO 7
u=u+RND
NEXT
FOR j=1 TO 8
u=u+RND*RND
NEXT
FOR j=1 TO 6
u=u+SQR(RND)
NEXT
FOR j=1 TO 3
u=u+SIN(RND*3)
NEXT |
Utilizzando Fa_Rnd.bas e StatFile, analizzate la variabile casuale U simulata da LimCentr.bas.
La versione forte del teorema spiega perché molti fenomeni in natura hanno distribuzione gaussiana: sono determinati dal contributo di tanti "piccoli" fattori casuali i cui effetti si sommano l'uno all'altro.
Ma … spesso si abusa della distribuzione normale.
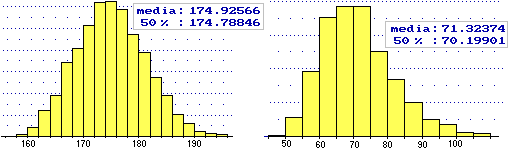
Illustriamo ciò a partire da un esempio "familiare". Sotto sono raffigurati gli istogrammi di distribuzione delle altezze e dei pesi rilevate alle visita di leva per la Marina del 1997 (primi scaglioni); si tratta di circa 4 mila maschi italiani ventenni.
| lato |
volume |
freq. |
| 1 |
1 |
1 |
| 2 |
8 |
2 |
| 3 |
27 |
3 |
| 4 |
64 |
4 |
| 5 |
125 |
5 |
| 6 |
216 |
5 |
| 7 |
343 |
4 |
| 8 |
512 |
3 |
| 9 |
729 |
2 |
| 10 |
1000 |
1 |
| |
Come si vede, mentre l'istogramma delle altezze ha forma approssimativamente gaussiana (come del resto si era già osservato nella scheda 2), ciò non vale per quello dei pesi.
Osserviamo, anche, che non è corretto dire che l'uomo medio ha altezza e peso medi (nel caso dell'esempio, che l'uomo ventenne medio è alto 174.9 cm e pesa 71.3 kg), anzi, l'uomo medio … non esiste. Vediamo perché a partire da un esempio più semplice.
Consideriamo 30 cubi, 1 di lato 1, 2 di lato 2, …, 1 di lato 10, come indicato nella tabella a lato. Per la distribuzione dei lati otteniamo l'istogramma sottostante a sinistra e per quella dei volumi l'istogramma a destra.
Il lato medio è 5.5, il volume medio è 247.5, che è diverso da 5.53. Quindi il "cubo medio" non esiste.
Invece il cubo del lato mediano è pari al volume mediano.
|
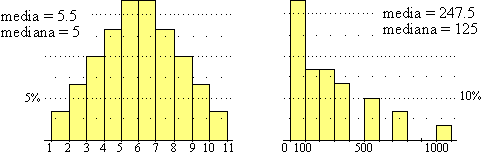
Ciò accade perché la funzione F: Lato 
Volume non è lineare; se lo fosse gli istogrammi avrebbero andamento simile e avremmo VolumeMedio = F(LatoMedio). Poiché F è crescente, cioè conserva l'ordine, abbiamo invece che VolumeMediano = F(LatoMediano) (ricordiamo che la mediana è il 50° percentile, cioè il valore del dato che sta a metà nell'elenco ordinato per valore dei dati).
Anche nel caso delle altezze e dei pesi delle persone possiamo mettere in relazione i valori mediani ma non quelli medi; infatti la funzione che associa ad ogni altezza (approssimata, ad esempio, ai millimetri) il peso medio delle persone di tale altezza è una funzione che è (almeno se si tratta di un campione abbastanza numeroso) crescente e non lineare (anche se, per motivi fisiologici, non è cubica come quella dell'esempio precedente); potremmo, eventualmente, dire che, nel 1997, l'italiano ventenne mediano aveva altezza di 174.8 cm e peso di 70.2 kg.
Per fare un altro esempio, non si può sostenere (come a volte accade in alcuni libri) che lunghezza e peso dei fagioli hanno entrambi distribuzione normale. Analogamente non si può sostenere che gli errori di misurazione hanno sempre andamento gaussiano: consideriamo un apparato misuratore ad alta sensibilità che rileva la grandezza A indirettamente, mediante un rilevamento della grandezza B, sfruttando una legge A=F(B); se gli errori di misurazione di B hanno una distribuzione gaussiana ma F non è lineare, gli errori di misurazione di A non possono avere distribuzione gaussiana.
Nota. A maggior ragione, di fronte a sondaggi che analizzano opinioni su argomenti diversi, non ha senso dire che "l'italiano medio pensa che … e che …".
Ad esempio se da una serie di interviste "a risposta chiusa" risulta che le preferenze per la musica rock sono il 32%, quelle per la musica pop il 29%, quelle per la musica classica il 21%, quelle per il jazz il 17%, e che le preferenze per i romanzi sentimentali sono il 33%, quelle per i romanzi d'avventura sono il 31%, quelle per i gialli sono il 25%, quelle per i racconti di fantascienza sono l'11%, pur ammettendo l'uso, improprio di "medio" per riferirsi alla scelta modale, non ha alcun senso dire che l'intervistato medio preferisce la musica rock e i romanzi sentimentali: non è affatto detto che – tra le coppie (rock, romanzo sentimentale), (rock, romanzo d'avventura), … , (jazz, fantascienza) – la coppia (rock, romanzo sentimentale) sia la più scelta.
Nel caso in cui le possibili scelte siano ordinabili si potrebbe parlare meno impropriamente di preferenza media ( scheda 2, §8, nota), ma solo relativamente a una singola questione: ha senso porsi il problema dell'esistenza di una relazione lineare tra due intervalli di numeri, non tra due generici insiemi ordinabili.