>>>>>

Scheda 6 - Problemi tipici della statistica matematica

3. Sulla STIMA dei PARAMETRI. Stimatori CORRETTI e NON DISTORTI.

    Abbiamo già osservato che all'aumentare di n la media statistica M_n(U) di una variabile casuale U ottenuta con n esperimenti converge (in probabilità) alla media teorica M(U) ( legge dei grandi numeri di Cebiscev). Quindi è naturale prendere come stima di M(U) la media statistica M_n(U). Più grande è il numero delle prove n tanto migliore è questa stima.

    Quando un parametro h della legge di distribuzione di una variabile aleatoria U è stimato con un valore h_n che è funzione degli n valori osservati di U (cioè con una "statistica": §1), si dice che h_n è una stima corretta (o consistente) di h se, all'aumentare di n, h_n converge (in probabilità) a h.

    Dunque la media statistica è una stima corretta della media teorica.

    Per stimare la varianza e lo scarto quadratico (sulla base di n osservazioni U₁, …, U_n di U) abbiamo sempre assunto 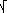V_n(U) = Σ (U_i–M_n(U))²/n e σ_n(U) = V_n(U).

    σ_n(U) non è altro che lo s.q.m. (nel senso della statistica descrittiva) di dato₁, …, dato_n dove dato_i è il valore assunto da U_i nel rilevamento.

    Anche questi sono stimatori corretti. Infatti V_n(U )= M_n((U–M_n(U)²) = M_n(U²)–M_n(U)² che converge in probabilità a M(U²)–M(U)² = V(U).

    C'è un altro motivo per cui possiamo ritenere "buona" la stima di M(U) mediante M_n(U). Illustriamolo con un esempio.

    Se effettuo 10 lanci di un dado (U è la variabile aleatoria che rappresenta l'uscita numerica del dado) e ripeto ciò più volte, il valore medio M₁₀(U) che di volta in volta ottengo varia casualmente. Tuttavia all'aumentare del numero delle volte per cui ripeto i 10 lanci, la media dei valori M₁₀(U) via via ottenuti converge (in probabilità) a M(U). Infatti se ripeto q volte 10 lanci la media delle q medie di 10 lanci non è altro che la media di q·10 lanci, e questa, per la legge dei grandi numeri, converge a M(U).

    In altre parole, non solo M_n(U) M(U) (in probabilità) per n , ma M₁₀(U) ha valore atteso M(U).

    Invece la media dei valori V₁₀(U) non converge (in probabilità) a V(U) [= 35/12=2.91666…], come si può verificare facilmente anche sperimentalmente, ad esempio mediante una simulazione al calcolatore: all'aumentare del numero delle volte per cui ripeto i 10 lanci, la media dei valori V₁₀(U) via via ottenuti non tende a stabilizzarsi su V(U), ma su un valore più basso.

1

 Effettua questo studio sperimentale con il programma sottostante (StimaVar.bas) e verifica se ottieni uscite simili a quelle sotto riportate.

 RANDOMIZE TIMER
 VT=35/12    ' var. teorica
 ne=10       ' num. degli esperimenti
 PRINT "Varianza teorica lancio 1 dado equo ="; VT
 PRINT "Media della varianza sperimentale con 10 lanci:"
 PRINT "n.prove", "media var", "media var / var teor"
 S=0 : n=0
 10
 FOR i=1 TO ne : x(i)=INT(RND*6)+1 : NEXT
 MEDIA x(),ne,m
 FOR i=1 TO ne : y(i)=(x(i)-m)^2 : NEXT
 MEDIA y(),ne,V
 n=n+1 : S=S+V
 IF n\500=n/500 THEN PRINT n, S/n, S/n/VT
 GOTO 10

 SUB MEDIA(x(),n,m)
 S=0 : FOR i=1 TO n : S=S+x(i) : NEXT
 m=S/n
 END SUB

   Varianza teorica lancio 1 dado equo = 2.916667
   Media della varianza sperimentale con 10 lanci:
   n.prove     media var    media var / var teor
    1000        2.64462        .9067267
    2000        2.632815       .9026794
    3000        2.640233       .9052226
    4000        2.64536        .9069804
    5000        2.636139       .9038191

    Le uscite tendono a stabilizzarsi attorno a 2.62…, non attorno al valore teorico; la terza colonna ci permette di congetturare che tendano a stabilizzarsi intorno a 9/10 di esso

    Si può in effetti dimostrare che V₁₀(U) converge (in probabilità) a V(U)·9/10 [= 35/12·9/10 = 2.625].

    Cioè, se approssimo V(U) con la varianza sperimentale relativa a 10 lanci, V₁₀(U), questa approssimazione non è soggetta solo all'"errore casuale" dovuto alla aleatorietà di V₁₀(U), ma anche a un "errore sistematico", dovuto al fatto che il valore atteso di V₁₀(U) non è V(U) ma V(U)·9/10.

    Più in generale, qualunque sia U, comunque prenda n, M_n(U) ha come media teorica M(U) mentre V_n(U) ha come media teorica V(U)·(n–1)/n. La dimostrazione non è banale, ma è possibile convincersi della validità di questa relazione studiando con opportune modifiche del programma altre situazioni (si vedano le considerazioni didattiche svolte prima del quesito 2 della scheda 5). Ad esempio posso cambiare il numero degli esperimenti, o posso cambiare anche il fenomeno (se studio la varianza statistica di RND+RND relativa a 5 esperimenti e la confronto con quella teorica, cioè 1/12+1/12=1/6, ottengo come rapporto tra la prima e la seconda circa 0.8, cioè 4/5).

    Quando un parametro h della legge di distribuzione di una variabile aleatoria U è stimato correttamente da un valore h_n, si dice che h_n è una stima non distorta di h se, ripetendo più volte le n prove, la media statistica dei valori h_n ottenuti converge (in probabilità) a h, ovvero (equivalentemente, per la legge dei grandi numeri) se M(h_n)=h.

    Quindi M_n(U) è una stima corretta e non distorta di M(U), mentre V_n(U) è una stima di V(U) corretta ma distorta: se sostituisco V(U) con V_n(U) aggiungo agli "errori casuali", dovuti alla aleatorietà di V_n(U), un "errore sistematico".

    Per ottenere uno stimatore corretto e non distorto di V(U) devo prendere V_n(U) · n/(n–1).

    Per σ(U) devo prendere σ_n(U) · (n/(n-1)), cioè
            √(Σ(dato_i-media)²/n) · √(n/(n-1)) =  √( Σ(dato_i – media)² / (n-1) )

    Naturalmente, poiché (n–1)/n tende a 1, e l'errore è (n–1)/n–1 = –1/n, per n sufficientemente grande V_n(U) e lo stimatore non distorto differiscono per un valore trascurabile (per n=100 differiscono dell'1%). Per valori piccoli di n può invece essere necessario utilizzare V_n(U)·n/(n–1), che (vedi sopra) può essere descritta direttamente come la somma dei quadrati degli scarti divisa per n–1.

Nota. A volte, specie sulle calcolatrici, mentre lo scarto quadratico medio statistico viene indicato σ_n, lo stimatore non distorto viene indicato σ_n-1, a ricordare che è calcolabile con la stessa espressione con cui si ottiene σ_n, a patto che a denominatore si metta n–1 invece di n; è una notazione un po' ambigua, perché σ_n–1 potrebbe essere interpretato come lo s.q.m. relativo a n–1 prove.
    Spesso si usa deviazione standard al posto di scarto quadratico medio (teorico) e viene chiamata deviazione standard statistica (o campionaria) lo stimatore corretto e non distorto dello scarto quadratico medio. A volte, però, con deviazione standard statistica viene indicato lo s.q.m. statistico (stimatore corretto ma distorto).

    Una spiegazione più semplicistica (ma che, a livello didattico, nella scuola secondaria, forse potrebbe essere sufficiente) per motivare la modifica rispetto alla espressione di V_n(U) è che questa è definita anche per n=1, e vale 0: mentre ha senso dire che un singolo dato ha dispersione nulla, non ha senso prendere questa come indicatore della dispersione della variabile casuale (che, se avesse dispersione nulla, sarebbe una variabile deterministica). La stima mediante V_n(U)·n/(n–1) è invece realizzabile solo se 2≤n.  Un altro modo di esprimersi sarebbe dire che dividiamo la somma dei quadrati degli scarti per il numero dei gradi di libertà (nel calcolare la varianza la media è fissata, e pone un vincolo tra i dati, per cui è solo da n-1 di essi che dipende il risultato: vedi §7).