>>>>>
Scheda 7- Analisi bivariata
7. Suggerimenti e risposte ai quesiti
Entrambi i procedimenti simulano una caduta casuale di proeittili, ma, mentre col primo essi
si distribuiscono in modo uniforme nel cerchio, col secondo si distribuiscono concentrandosi
maggiormente intorno a (0,0). Riferendosi al secondo nella forma di script, il valore assunto
da a non influisce sulla caduta nel cerchio piccolo, che dipende
solo dal valore assunto da r; poiché r
è distribuito uniformemente e coincide con la radice di x*x+y*y, la frequenza
tende alla probabilità che random() sia minore di 1/2, cioè a 1/2.
I due procedimenti di per sé non sono sbagliati.
È il fenomeno da simulare che non è stato caratterizzato a suffiecienza: una caduta casuale può avere diverse leggi di distribuzione.
Torna al punto 1
|
È la funzione che a ogni (x,y) del cerchio associa il valore 1/π e agli altri punti associa 0. Il volume del cilindro verticale che essa delimita assieme al piano z=0 ha volume 1.
Torna al punto 2
Le curve di livello sono cerchi concentrici.
Il volume è 1, per cui il cono deve essere alto 3/π: questo è f(0,0).
Il raggio delle curve di livello varia linearmente con la quota (se questa è compresa tra 0 e 3/π).
Torna al punto 3
|
bersaglio-1
 |
Nel caso di BERSAGL1 e BERSAGL2 X e Y sono dipendenti: ad es. se X è vicino a 1 Y deve per forza essere vicino a 0, affinché (X,Y) stia nel cerchio. Per il sistema che ha funzione densità che ha come grafico il cono valgono considerazioni analoghe.
Invece, nel caso del lancio di due dadi, la distribuzione raffigurata all'inizio del §2 sottointende l'ipotesi che gli esiti dei due dadi sono indipendenti (se no, certe uscite sarebbero più frequenti di altre). L'ipotesi di indipendenza (vedi scheda 3) corrisponde, nel caso finito (e nel caso sperimentale), alla proporzionalità tra le righe o tra le colonne della tabella a doppia entrata e, passando all'istogramma tridimensionale, corrisponde alla proporzionalità tra le altezze delle righe di colonnine o tra le altezze delle file di colonnine. Nel caso dei dadi righe e file di colonnine sono tutte uguali.
Passando alle funzioni di densità al posto delle righe e delle file di colonnine si considerano le sezioni parallele al piano xz e le sezioni parellele al piano yz: due qualunque sezioni, ad esempio parallele al piano xz, devono essere ottenibili una dall'altra mediante una dilatazione/contrazione verticale. Nel caso delle funzioni densità finora considerate ciò non accade mai: ad esempio la sezione determinata dal piano yz non ha lo stesso andamento (a meno di un fattore di scala) di nessuna delle altre sezioni ad essa parallela.
Torna al punto 4
Potrebbero essere, ad es., la altezza di una persona di eta` e sesso fissati e la altezza di suo padre: hanno entrambe andamento gaussiano e sono correlate (ma non dipendenti deterministicamente).
Torna al punto 5
|
A lato è riprodotto l'isotogramma richiesto.
Torna al punto 6
Nelle due sottopolazioni (maschile e femminile) il coeff. di correlazione è più basso. Unendo le due "nuvole" si ottiene una nuvola più allungata, il che dà luogo a un coefficiente di correlazione maggiore.
Torna al punto 7
Per B1 e B2 si ottengono rette di regresso quasi parallele agli assi, infatti X e Y teoriche sono scorrelate e anche nel caso sperimentale il coeff. di correlazione è quasi nullo.
|
 |

Nel caso di terraria c'è un alto coeff. di correlazione (0.91).
La retta di regresso richiesta ha coeff. direttivo 1.4.
Con cosiderazioni teoriche si poteva arrivare a conclusioni analoghe: la distanza lungo la strada sicuramente è maggiore di quella in linea d'aria; supposto di essere in una regione dalle caratteristiche geografiche non molto diversificate e che non presenti territori invalicabili (a causa di catene montuose a picco, di insenature o laghi molto grandi) essa dovrebbe crescere più o meno proporzionalmente alla distanza in linea d'aria; per stimare il rapporto tra l'una e l'altra, tenendo conto delle curve supponiamo che esso sia circa pari al rapporto che c'è tra la strada per raggiungere due vertici opposti di un quadrato passando per il bordo o la strada diretta, cioè  2 = 1.4 circa.
2 = 1.4 circa.
Torna al punto 8
Si dovrebbero ottenere rappresentazioni simili alle seguenti.
La diversa divaricazione delle rette di regresso suggerisce il diverso livello di correlazione.
 |
r(D,B) = 0.4581852
M(D) = 74.42326 min: 47 max: 96
M(B) = 70.47674 min: 48 max: 126
y=ax+b a=0.7664956 b=13.43164
x=ay+b a=0.2738877 b=55.12055
|
r(A,B) = 0.6974944
M(A) = 91.18753 min: 48 max: 179
M(B) = 70.47674 min: 48 max: 126
y=ax+b a=0.940987 b=-15.32954
x=ay+b a=0.5170087 b=54.75044
|
 |
Osserviamo come, di fronte a grandi quantità di dati, l'uso di un
istogramma (figura sotto a sinistra, o a destra, in forma poliedrica) consente di integrare le informazioni che si possono ricavare dal
diagramma di dispersione (nel quale non si riescono a distinguere le zone più fitte in quanto i
punti si sovrappongono, anche se in alcuni programmi, come nel caso di Stat [se si aziona [Plot] con "c"
nel box N], ciò viene realizzato con un cambiamento nel colore dei punti).
Sotto a destra è riportato un istogramma (non normalizzato) del campo "pesi"; si vede bene la forma non gaussiana (vedi scheda 5, §2).
 |
Analisi del campo B
4170 dati in 4170 righe min,max: 48,126
media: 70.4767386 mediana: 70
5% :55 25% :63 50% :70
95% :90 75% :76 percentili
----|--|===|=|------|-----------------
|
|
A lato sono riprodotti rette di regresso e assi principali di Ellisse.Tab.
Torna al punto 9 |
 |
•
Con la retta di regressione non vengono utilizzate le informazioni sulla precisione delle misure.
Poi non si tiene conto del "punto esatto" (H,F)= (0,0) (cioè del fatto che
b deve essere 0); il metodo andrebbe bene se si analizzassero i dati della lunghezza dell'elastico
non conoscendo la lunghezza a riposo. Sotto a sinistra è raffigurato lo studio "errato" del
problema realizzato con Stat; aggiungendo il punto (0,0) si otterrebbe una valutazione migliore (figura a destra), ma non corretta: il punto (0,0) viene considerato comunque "casuale", non esatto.

• Volendo usare un metodo di minimizzazione occorrerebbe imporre che la retta passi per (0,0) (non per il baricentro, come accade con la regressione),
cioè cercare la funzione di diretta proporzionalità f: x  kx per cui
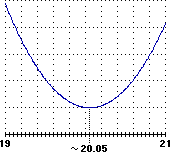
è minima la somma dei quadrati degli scarti, V=(11k–220)2+(16k–350)2+… (vedi la figura seguente).
kx per cui
è minima la somma dei quadrati degli scarti, V=(11k–220)2+(16k–350)2+… (vedi la figura seguente).
 |
Volendo, con metodi algebrici, si può trovare anche l'espressione di k in funzione dei dati sperimentali. Nel triennio questa espressione può essere trovata anche con tecniche differenziali (è una funzione a un argomento facilmente derivabile).
• Sempre nelle situazioni in cui non si conosca la precisione dei dati sperimentali, nei rari casi in cui si abbia a che fare con valori ottenuti mediante apparati misuratori ad alta sensibilità, si può ricorrere anche al metodo (b), che, nel triennio, consente anche di valutare l'indeterminazione del risultato.
• Volendo si potrebbe anche cercare la funzione di diretta proporzionalità f: x  kx per cui è minimo il valore V seguente: kx per cui è minimo il valore V seguente: |
|
V=|f(11)-220|+|f(16)-350|+… =|11k–220|+|16k–350|+…
Studiando graficamente V in funzione di k (si tratta di una funzione continua lineare a tratti). Si ottiene:
k=20.0
Questo metodo ha tuttavia il limite di non fornire una valutazione della precisione del valore trovato.
Dal punto di vista tecnico il procedimento (a) è il più corretto e il più semplice tra quelli proposti, anche se a molti può apparire inusuale: è l'unico che tiene conto delle precisioni associate alle misure. |
 |
È un metodo generale che va bene quando si ha a che fare con valori ottenuti mediante strumenti di misura a bassa sensibilità (indeterminazione=divisione della scala graduata) o, comunque, di cui si conosca l'indeterminazione. Quando la legge non è lineare si può estendere il metodo ricorrendo a scale logaritmiche o al tracciamento di fasci di curve mediante un programma al computer.
Dal punto di vista didattico possiamo osservare che (a), pur essendo corretto e usato nella ricerca fisica, è utilizzabile sin dalla scuola media inferiore.
Altrettanto corretto e praticabile scolasticamente (a partire dal biennio della scuola secondaria superiore) è il seguente procedimento:
• calcolare gli intervalli di indeterminazione dei valori F/H relativi alle quattro prove, cioè: [215/13,225/9] = [16.538…,25], [345/18,355/14] = [19.166…,25.357…], … e farne l'intersezione.
Si riottiene, ovviamente, lo stesso intervallo [19.08,21.25] ottenuto con il metodo (a).
Abbiamo tentato di problematizzare culturalmente e didatticamente l'uso delle tecniche statistiche considerate nel quesito. Spesso, invece, nelle attività di laboratorio, ma anche negli esempi di applicazione della statistica presenti nei libri di matematica, vengono utilizzati metodi che gli alunni non sono in grado di padroneggiare (per assenza di strumenti formali) e che non sono adeguati alle situazioni: calcolare media e dispersione di più misure ottenute con uno strumento a bassa sensibilità, usare senza motivazioni teoriche la deviazione standard o formule per la propagazione degli errori, … . Si veda anche quanto discusso nel §4 della scheda 6.
Torna al punto 10



 2 = 1.4 circa.
2 = 1.4 circa.






 kx per cui
è minima la somma dei quadrati degli scarti, V=(11k–220)2+(16k–350)2+… (vedi la figura seguente).
kx per cui
è minima la somma dei quadrati degli scarti, V=(11k–220)2+(16k–350)2+… (vedi la figura seguente). 
