4a SCUOLA ESTIVA PER INSEGNANTI   UMI CIIM – AIRDM  (vedi)

La statistica e l'avvio al pensiero probabilistico:
come passarsi la palla tra un livello scolastico e l'altro?
quali rapporti con le altre aree della matematica e con le altre discipline?

Carlo Dapueto - DiMa - UniGe

http://macosa.dima.unige.it/ciim

1. Presentazione
2. Attività laboratoriali
3. Discussione collettiva

1. Presentazione

•  Questa presentazione e queste attività sono proposte assieme per la scuola secondaria sia di primo che di secondo grado. Perché?

•  Come è organizzato il lavoro.

•  Potete ritrovare tutto all'indirizzo web sopra ricordato.

•  Sarebbe stato utile (specie per attività statistico-probabilistiche) svolgere attività al computer. Farò comunque qualche riferimento ad esse e metterò dei link nel documento.

[Ho modificato questa notte il documento sulla base delle cose sentite ieri; c'è qualche cosa che potrebbe essere corretto nella versione finale]

•  La prima area della matematica che storicamente si è sviluppata (anche se solo ai primi livelli) è la statistica.

•  All'inizio per fare dei confronti quantitativi.  Poi anche per fare delle previsioni;  quindi intrecciandosi anche con aspetti probabilistici.  Solo successivamente, come "prolungamento", si è sviluppato anche il calcolo probabilistico relativo ad eventi che non si ripetono.

•  Sono recenti gli studi degli intrecci tra probabilità e statistica. È ancora più recente una prima definizione matematica di probabilità, che non può che essere assiomatica, come del resto sono gran parte delle definizioni matematiche.  Anche nella scuola primaria gran parte dei concetti vengono introdotti assiomaticamente, cioè attraverso delle regole mediante cui operare con essi (anche se non si chiamano esplicitamente presentazioni "assiomatiche"). Su ciò eventualmente torneremo.

•  La questione è come sviluppare questi aspetti nell'arco scolastico: come introdurli, come/quando formalizzarli, con quali applicazioni alle altre aree del sapere, matematico e non.  La scuola (nonostante le precise indicazioni dei bellissimi programmi messi a punto tra il 1979 e il 1987), soprattutto quella superiore, non si è - "in genere" - mai occupata di statistica e di probabilità, se non, ora, alla fine delle superiori, costretta dalle prove finali. Sui motivi di ciò non ci soffermiamo.  In vero nei libri di testo la probabilità è comparsa da un po' di anni, ma (quando parlo di libri di testo mi riferisco ai libri di testo più diffusi), ma sarebbe meglio che non fosse accaduto: strane pseudodefinizioni, buffi esercizi di calcolo combinatorio, applicazioni strampalate di concetti non banali. Vedermo qualcosa.

•  Metteremo qualche link ad approfondimenti e ad esercizi che non avremo il tempo di affrontare.

Cose che si possono avviare nella scuola dell'infanzia (flash)

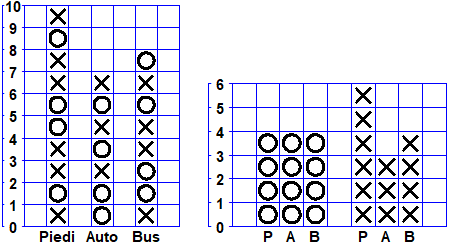Nell'istogramma a quadretti a lato ogni alunno, maschio (X) e femmina (O), ha indicato il modo (a piedi, in automobile o coll'autobus) in cui di solito arriva a scuola

Il tempo atmosferico (gli istogrammi che sintetizzano i dati via via raccolti su un tabellone)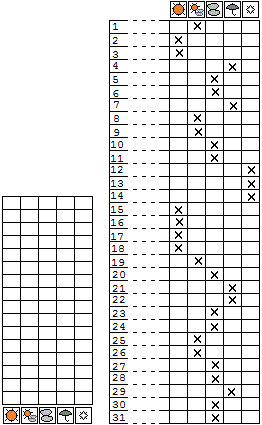

Nella scuola elementare si possono avviare attività più complesse (flash)

Indagine statistica su grandi campioni (gli alunni di una scuola, e i loro genitori e nonni) in cui sono coinvolte tutte le discipline (la elaborazione matematica coinvolge tutte le aree, e consente anche di avviare all'idea che aumentando i dati le uscite si stabilizzano, gli istogrammi tendono a diventare delle curve, …)
 

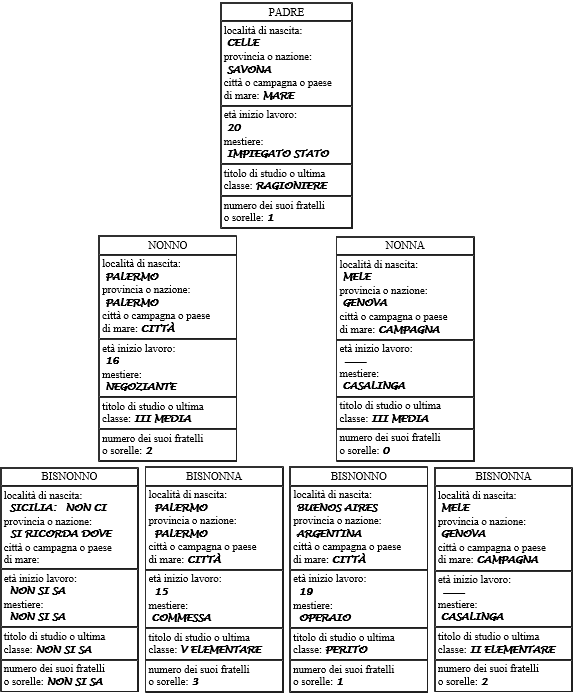
Nella scuola media gli sviluppi possono essre molteplici.

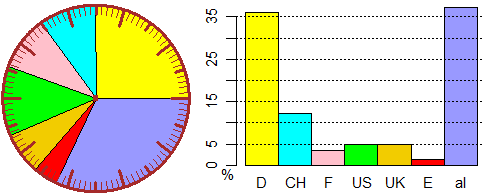
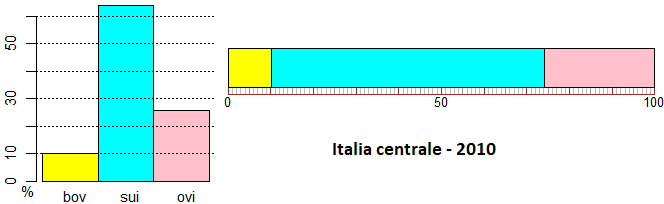
Turisti stranieri in Liguria nel 2001. Il diagramma a settori circolari rappresenta come si sono distribuiti gli arrivi per paese di provenienza. L'istogramma illustra come si sono distribuiti i giorni di soggiorno.

[inzialmente si possono usare cerchi già graduati in 100 parti: fatti col computer dal docente]

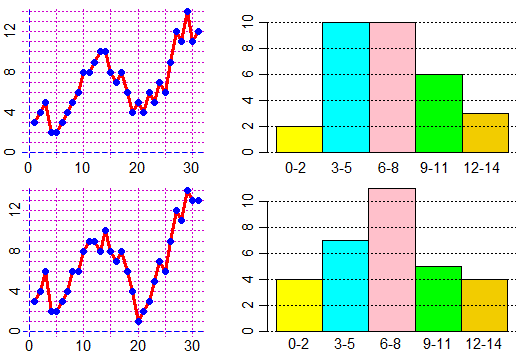
Grafici della temperatura in due particolari città italiane alle dodici nei giorni di un dato mese e, non necessariamente nello stesso ordine;  i relativi istogrammi.
(1) A quale mese si riferiscono: febbraio, luglio od ottobre?
(2) Associa ogni grafico al corrispondente istogramma, e motiva la risposta

Diagrammi a barre e a striscia

Ovviamente nella scuola media, introdotti gli strumenti nei contesti, si possono/devono fare anche degli esercizi di consolidamento tecnico, e degli esercizi astratti:

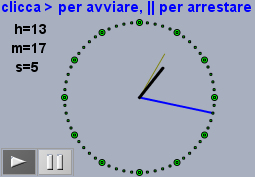
Aprite con Cinderella questo file: clicca.  Otterrete un orologio simile a quella a lato, che potete avviare e arrestare con dei clic. Usatelo in classe per misurare il tempo in secondi che passa effettivamente tra quando voi inziate e quando finite di contare 1, 2, 3, …, 60 cercando di impiegare un minuto. Provate a fare ciò due o tre volte ciascuno di voi. Poi mettete insieme i dati e trovatene il valor medio. È vicino o lontano da 60? t = c(45,52,67,56,57,65,44,50,59,43,55,72,51,58,70,56, 63,60,48,55,68,50,49,70,49,63,58,65,44,50,49,63, 52,67,48,59,43,55,72,51,58,63,60,55,68,50,49,57) mean(t) 56.47917 stem(t) 4 | 3344 4 | 5889999 5 | 00001122 5 | 5555667788899 6 | 003333 6 | 557788 7 | 0022

Prima di usare Cinderella è bene usare un normale orologio. I primi stem-and-leaf vanno fatti a mano, usando la carta quadrettata (è uno strumento efficace e facilissimo da usare).  Poi, imparato ad usarlo, si può usare il computer.  Se i dati sono molti, del computer non si può fare a meno (la statistica si è sviluppata in modo decisivo dopo la comparsa del computer).

stem-and-leaf plot | | | | | | | | | | | | | | | | | | 5| |6|9|9| | | | | | | | | | | | | | 6| |1|1|2|3|4|4|4|4| | | | | | | | | 6| |6|6|6|6|7|8|8|8|8|8|8|8|9| | | | 7| |0|0|0|0|0|0|0|0|0|0|1|3|3|3|3|4| 7| |5|7|7|7|7| | | | | | | | | | | | 8| |0|0|1|2|2|4| | | | | | | | | | | 8| |6|6|6|6|8| | | | | | | | | | | | 9| | | | | | | | | | | | | | | | | | 9| |7| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |

Paolo ha raccolto il seguente elenco di dati; si tratta dei pesi (arrotondati ai kg) degli alunni maschi dell'ultimo anno della scuola superiore che frequenta. 64, 66, 73, 86, 70, 75, 68, 86, 88, 63, 73, 70, 69, 66, 77, 80, 80, 77, 82, 61, 77, 71, 59, 84, 86, 70, 77, 70, 97, 68, 66, 70, 70, 68, 70, 68, 81, 73, 61, 73, 59, 70, 68, 67, 70, 68, 64, 82, 86, 66, 68, 74, 64, 64, 62, 56, 70. Decide di riorganizzare i dati sulla carta quadrettata nel modo illustrato a sinistra.

Si noti che l'andamento dei pesi non è simmetrico (su ciò si tornerà).

Un altro aspetto che lega la statistica alle altre aree della matematica è la questione degli arrotondamenti, anche questi poco "assimilati" dai mass media (e dai libri di testo ...). Un esempio.

Il censimento del 1970 ha valutato in 627 776 la popolazione di Boston.  Sappiamo che questo dato può essere affetto da un errore del 2%.  Se alla televisione hanno detto che la popolazione era di circa 627776 abitanti, ti sembra corretta questa comunicazione?

627776·98/100 = 615220.48,   627776·102/100 = 640331.52.
Per esprimerci sinteticamente e in modo comprensibile da tutti potremmo dire che è "circa 630 mila". In modo più preciso potremmo dire che è 628±13 mila.  Non ha alcun senso dire che la pololazione era di circa 627776 abitanti.

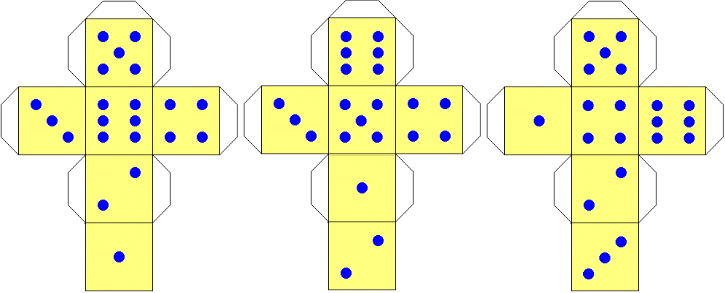
Lanciare dadi costruiti con il cartoncino (del tipo di quelli che si trovano in edicola), e costruire gli istogrammi. Non sono dadi equi (per altro, i dadi equi non esistono …).

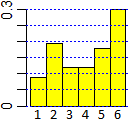Poi fare anche esercizi di questo tipo: Le uscite di un particolare dado da gioco non equo hanno la legge di distribuzione rappresentata dall'istogramma a sinistra. Valuta la probabilità che lanciando due dadi di questo tipo esca 11. [l'istogramma a destra può essere poi costruito in classe]

età dei morti in Italia nel 1951 per classi di età

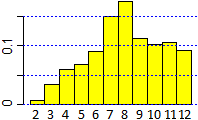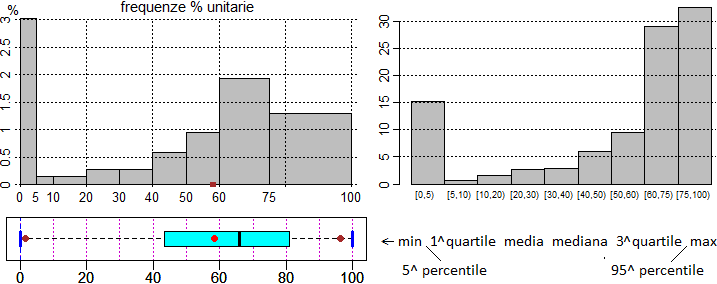
Occorre, poi, usare del software per fare delle rappresentazioni corrette. Sopra a sinistra quello che si può ottenere con R, a destra quello che si riesce ad ottenere con un foglio di calcolo! (i fogli di calcolo sono strumenti "complicati" - per essere ben usati - e inefficienti per fare della statistica, come dicono tutti i ricercatori di statistica che io conosco [vedi qui e qui].

I box-plot sono uno strumento facile da usare e fondamentale per fare analisi statistiche di ogni tipo. A questo punto stiamo affrontando attività da collocare nella scuola secondaria superiore.

Morti per classi di età in Italia nel 1881-1890, nel 1951, nel 1988, nel 2006

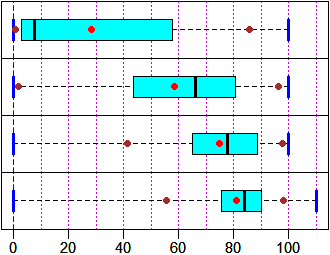Un altro flash: interazioni con le lingue, l'italiano, … (l'analisi statistica è uno strumento usato per identificare gli autori: lunghezza frasi, punteggiatura, ...)

"Alice in Wonderland" in Italiano e in English

Alcune cose scontate su cui non mi soffermo (proprietà della probabiità, che sono esattamente le stesse delle "percentuali" in ambito statistico,  e grafi):

Il bersaglio raffigurato a lato viene colpito nella zona A con probabilità 0.14, nella zona B con probabilità 0.22, nella zona C con probabilità 0.19. Qual è la probabilità che un generico tiro non colpisca il bersaglio?    Pr(non colpito il bersaglio) = 1 − Pr(colp. il bersaglio) = 1 − (Pr(colp. A)+Pr(colp. B)+Pr(colp. C)) = 0.45 = 45%.

Una partita di semi ha un tasso di germinazione del 70%. Piantando due semi, qual è la probabilità che germini una sola pianta?

ed una cosa meno ovvia, rispetto alla pratica didattica diffusa:

	Quali sono media e mediana della variabile casuale di cui a sinistra è rappresentata graficamente (senza specificazione della scala orizzontale) la funzione densità?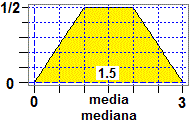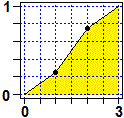
	(simmetria assiale → media = mediana = 1.5)

Un aspetto importantissimo è la simulazione, basata sulla possibilità di generare numeri a caso con distibuzione uniforme. Qui e qui puoi trovare qualche informazione sul generatore di numeri (pseudo)casuali;  qui puoi trovare una scheda per la 2ª o la 3ª superiore.  Vediamo un esempio, affrontabile nel triennio finale della scuola superiore, senza soffermarci sul modo in cui è stimata la precisione dei valori via via ottenuti.

Non preoccupiamoci di capire il seguente programmino in R, ma usiamolo (per caricare R vedi qui) copiando le seguenti righe:

source("http://macosa.dima.unige.it/r.R")

SUC <- function(i) ifelse(i==3,1,i+1)

Event = function() {
 V = 0; x = NULL; y = NULL; Lato = 8; Diam = 1; L = Lato-Diam
 for(i in 1:3) { x[i] = runif(1)*L+1/2; y[i] = runif(1)*L+1/2 }; i=1
 while(i<=3) { j=SUC(i); k=SUC(j); d=point_line(x[i],y[i], x[j],y[j],x[k],y[k]); 
               i=i+1; if(d < Diam) {V = 1; i = 4} }; x <<- x; y <<- y; V }

genera = function() {
  polyC(c(0,8,8,0),c(0,0,8,8),"yellow")
  n = ifelse(Event(),1,0)
  text(0.5,0.5,n); text(7.5,7.5,n); text(0.5,7.5,n); text(7.5,0.5,n)
  for(i in 1:3) {circleC(x[i],y[i], 1/2, "white");circl(x[i],y[i], 1/2, "blue")}
  polyC(x,y, 0);  }

rowcol(3,5); for(i in 1:15) {BoxmW(0,8, 0,8); genera()}
rowcol(3,5); for(i in 1:15) {BoxmW(0,8, 0,8); genera()}
# ...

Ecco cosa si ottiene graficamente:

 

...

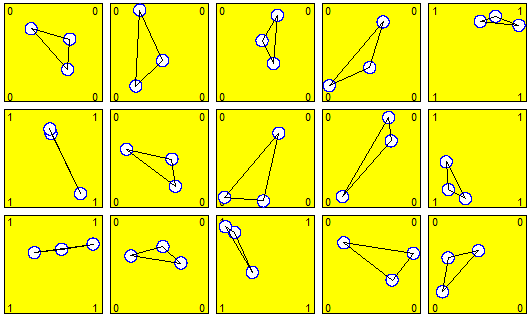
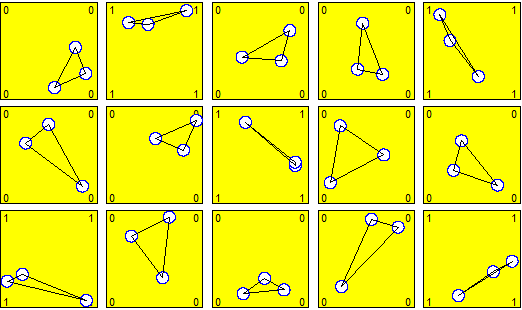
È un problema non facile da risolvere teoricamente. Bisognerebbe impiegare un bel po' di tempo, se si è capaci, per risolverlo, e non sarebbe affatto facile controllare la correttezza della soluzione. Con le seguenti istruzioni, sulla base del procedimento descritto (di cui abbiamo visto che possiamo controllare la correttezza graficamente) abbiamo:

PR = function(n) {f = 0; for (i in 1:n) f = f + ifelse(Event(),1,0);
       fr = f/n; S = sqrt(fr*(1-fr)/(n-1)); cat(fr*100, "+/-", 3*S*100,'\n') }

n=10000; cat(n,"  "); PR(n)
n=n*4; cat(n,"  "); PR(n)
# 
# ...
# n=n*4; cat(n,"\t"); PR(n)
# 10240000   42.05155 +/- 0.04629099

Qui ci fermiamo, per brevità, alle prime uscite, ottenendo 42.3 +/- 0.8. Andando avanti, avendo un po' di minuti a disposizione, possiamo ottenere valori più precisi (42.05±0.05).

Analogamente (vedi qui) posso trovare che la probabilità di trovare almeno un tris (cioè 3 o 4 carte dello stesso valore) in 10 carte estratte da un mazzo da 40 carte è:

PR(1e7)
# 38.43589 +/- 0.04614807      ie: (38.44±0.05)%.

[Vedi qui se vuoi vedere come possono essere introdotti gli eventi e le variabili casuali,  qui se vuoi vedere una precisazione sul significato degli intervalli di indeterminazione trovati con le simulazioni]

La probabilità e la statistica, a parte alcuni concetti sviluppabili negli ultimi due anni delle superiori, usano in gran parte gli stessi strumenti impiegati per le altre aree della matematica:  ciò che le differenzia dalle altre aree è che i problemi statistico-probabilistici sono (quasi) sempre riferiti a dei contesti:
(1) con i contesti occorre sporcarsi le mani,
(2) con le altre aree della matematica occorre integrarsi.
È questo che, purtroppo, sconvolge molti insegnanti.

Al terzo anno delle superiori, in particolare, quando si introducono (o di dovrebbero introdurre) il calcolo differenziale integrale, sia per la matematica che per la fisica, questi concetti possono essere introdotti (prima, dopo o contemporanemente) per il calcolo delle probabilità. Possiamo vedere qui un flash sulla distribuzione triangolare.  Sotto sono richiamate alcune delle varie funzioni di distribuzione che si possono studiare, e il cui studio si intreccia molto bene con quello dell'analisi matematica (ma senza ridurlo ad esercizi di analisi).

(vedi)

Un aspetto importantissimo, per non banalizzare gli usi e le applicazioni della matematica, è mettere a fuoco che il calcolo probabilistico non basta per fare delle scelte. Un semplice esempio:

X, noto professionista, arrivato alla stazione per prendere il treno per un importante viaggio di lavoro, si accorge di aver dimenticato la carta di credito e di aver nel portafoglio solo 20 euro, insufficienti per il biglietto: mancano 15 euro. Allora X decide di scommettere 15 euro (con un'altra persona) che giocando a bim-bum-bam esca un numero multiplo di 3. Secondo voi la decisione di X è conveniente? E per l'altra persona?

La probabilità che X vinca la scommessa è solo 1/3 (fate il calcolo, tenendo conto che le uscite a bim-bum-bam sono analoghe a quella del lancio di 2 dadi): la scommessa non è equa.  Ma se perdere il treno comporta un danno economico ben superiore a quanto X dovrebbe sborsare perdendo la scommessa, la scelta operata da X è da considerare conveniente. Ovviamente, anche per l'altra persona la scomessa è conveniente. Qualche volta si possono accontentare tutti …

È evidente il ruolo del calcolo delle probabilità nella razionalizzazione delle situazioni "incerte".
Esso non è tuttavia sempre sufficiente: si pensi ai vaccini, che a volte hanno una certa probabilità di causare l'insorgere delle malattie stesse; per decidere se rendere obbligatoria una vaccinazione non basta trovare che tale probabilità è bassa rispetto alla diffusione della malattia: imporre a chi potrebbe rimanere sano una vaccinazione che può causare una malattia comporta valutazioni anche di tipo morale.
Vi sono anche casi in cui si ricorre a valutazioni probabilistiche erronee perché basate su campioni mal scelti o per altri difetti metodologici:  tipico è l'esempio di un sondaggio telefonico che può avere come risposta A o B in cui si tenga conto solo di chi accetta di rispondere senza considerare il fatto che coloro che non vogliono rispondere potrebbero, per la natura della questione, essere più inclini a una delle due risposte.

E vi sono casi in cui se ne fa un uso improprio, ad es. quando si confonde la presenza di una relazione di dipendenza probabilistica con la presenza di un legame di causa-effetto [Pr(A|B) indica la probabilità dell'evento A nella condizione che si verifichi l'evento B]:

Un gruppo di medici, utilizzando indagini statistiche, ha concluso che la malattia X (che fino ad allora si riteneva fosse causata dal tipo di alimentazione) è essenzialmente dovuta a fattori genetici.  Infatti dalle statistiche ha dedotto che:

Pr("avere X" | "avere genitori o fratelli con X") > Pr("avere X" | NOT "avere genitori o fratelli con X")

Vi sembra corretta questa conclusione? Perché?

Se X è una certa malattia o un certo comportamento, il fatto che esso si riscontri più facilmente tra familiari, più precisamente il fatto che Pr("avere X" | "avere genitori o fratelli con X") > Pr("avere X" | NOT "avere genitori o fratelli con X"), non permette di concludere che all'origine di X vi siano essenzialmente fattori genetici.  Infatti i fattori principali potrebbero essere di tipo ambientale o sociale, e la relazione probabilistica trovata potrebbe essere dovuta al fatto che è più facile condividere usi, costumi e ambienti con un familiare che con un estraneo.

Non è solo questione di formule!!!

Sospendiamo qui la prima fase dell'incontro. Ora incominciamo a "lavorare".

2. Attività laboratoriali

Provate (a gruppi) ad affrontare i questiti e a mettere a fuoco i problemi didattici proposti.

1.  Indica tra i seguenti istogrammi quale può rappresentare la distribuzione:
(1) dell'età dei morti in un paese sviluppato,
(2) dell'età dei morti in un paese sottosviluppato,
(3) dell'altezza delle femmine adulte di una città,
(4) delle altezze degli adulti (maschi e femmine) di una città.

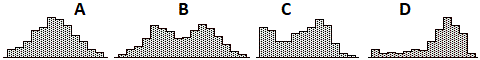
(a) Motiva in modo semplice (al livello di ragazzi di 13 anni) la risposta.
(b) Quali obiettivi didattici possono avere esercizi del genere?  Quando potrebbero essere inseriti nel percorso didattico?

2.  Una vetrina di un negozio viene infranta e viene prelevata parte della merce esposta.  Un testimone afferma che il ladro era arabo.  Quando gli inquirenti gli ripropongono scene simili in analoghe condizioni di luce, distanza, … il testimone identifica correttamente la razza (arabo, non arabo) del ladro nel 75% dei casi.  È attendibile la testimonianza se nella località considerata il 12% dei furti sono opera di ladri di razza araba?  [per rispondere calcola la probabilità che il ladro sia effettivamente un arabo]

Non è un questito banale.
(a) Con quali strumenti affrontarlo?
(b) È utile far "scontrare" gli alunni con esercizi di questo genere, perché si rendano conto della facilità di ingannarsi, o è meglio affrontare solo esercizi più semplici?

3.  Cinque ragazzi devono sorteggiare tra di loro un pallone.  Decidono di estrarre ciascuno uno stecco da un mazzetto composto da 5 stecchi di legno tra i quali uno è più corto degli altri. Vince il premio chi estrae lo stecco più corto.  Ma Giorgio e Gabriella non sono d'accordo. Ritengono che il primo a estrarre sia avvantaggiato . Hanno ragione o torto?  Come convincere Giorgio e Gabriella o gli altri tre ragazzi che hanno torto?

È un problema "facile"! (qual è la risposta?)
Ma la scuola, la nostra scuola, ci "educa" ad affrontarlo in modo sbagliato. Perché?

4.  In un ospedale sono rilevati i dati relativi alla frequenza cardiaca a riposo di 10 individui e i loro anni complessivi di istruzione.  Rappresentiamoli nel piano (durata istruzione, frequenza) e approssimiamone l'andamento con una retta.

soggetto	1	2	3	4	5	6	7	8	9	10
Anni di istruzione	12	16	13	18	19	12	18	19	12	14
Battiti al minuto	73	67	74	63	73	84	60	62	76	71

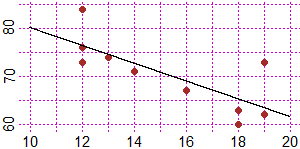
C'è una forte associazione tra una lunga scolarizzazione e una bassa frequenza cardiaca a riposo.
(a) Ciò indica la presenza di una relazione di causa-effetto?
(b) Quali questioni didattiche propone questo esempio?
(c) Si può quantificare la relazione col concetto di correlazione e precisare l'andamento con la retta di regressione; è necessario avere già affrontato questi concetti per mettere a fuoco il problema?

lato   volume  freq. 1 1 1 2 8 2 3 27 3 4 64 4 5 125 5

lato   volume  freq. 6 216 5 7 343 4 8 512 3 9 729 2 10 1000 1

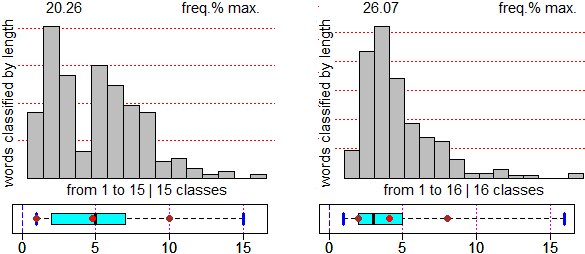
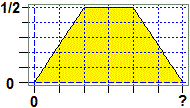
5.  Consideriamo 30 cubi, 1 di lato 1, 2 di lato 2, …, 1 di lato 10, come indicato nella tabella a lato. Sotto sono rappresente graficamente la distribuzione dei lati e quella dei volumi. Il volume mediano è cubo del lato mediano? Il volume medio è il cubo del lato medio? [se i dati sono in numero dispari, stiamo assumendo come "mediana" il primo dei due dati centrali vedi]

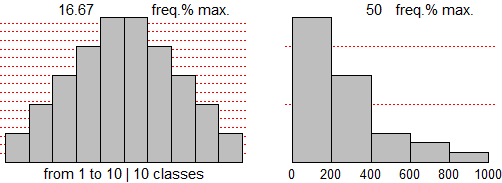
È un esempio semplice che introduce alcuni utili elementi di "vaccinazione".
(1) Se una popolazione di pesci ha lunghezze con andamento gaussiano, hanno andamento gaussiano anche le loro masse?
(2) Sono pochi e fenomeni con andamento gaussiano: che ruolo ha la gaussiana? quando introdurla a scuola?
(3) Quale ruolo possono/devono avere nell'insegnamento la mediana e i percentili?

6.  Nel dizionario Sabatini-Colletti, (ed. 2012) per la voce "probabilità" si legge:
1 mat. Concetto fondamentale intorno al quale si sviluppa la formalizzazione matematica dei fenomeni casuali; nella teoria classica è definita come il rapporto tra il numero dei casi in cui l'evento può verificarsi e il numero dei casi possibili || calcolo delle p., teoria, derivata da quella classica e da altre più recenti, che formalizza i concetti relativi alla p.
2 estens. Possibilità che si ritiene possa tramutarsi in realtà: non ha nessuna p. di vincere || con tutta, con ogni p., molto probabilmente, quasi certamente
Nel Longaman Dictionary (ed. 1978) per la stessa voce si trova:
1  the state or quality of being probable   2  likelihood (there's little probability of reaching London tonight)   3  a probable event or result (war is a serious probability in the present state of affairs)   4  (in MATHEMATICS) the chance of an event happening, expressed as a calculation based on known numbers   5  The branch of MATHEMATICS concerned with such calculations.

Quale delle due impostazioni è migliore?  Perché?

Traduzione letterale dal "Longaman":   1 lo stato o la qualità di essere probabile  2 verosimiglianza (c'è poca probabilità di raggiungere Londra stasera)  3 un evento o un risultato probabile (la guerra è un grave probabilità, allo stato attuale delle cose)  4 (in Matematica) la possibilità che accada un evento, espressa come un calcolo basato sui numeri noti  5 Il ramo della Matematica che si occupa di tali calcoli

3. Per la discussione della seconda parte indirizzo ai commenti ad esercizi analoghi che sono presenti in rete, e faccio seguire alcuni commenti.

Problema 1. (associare istogrammi a fenomeni - serve conoscere la materia coinvolta)
    vedi.

Problema 2. (le testimonianze ... - e la probabilità condizionata)
    vedi.

Problema 3. (sorteggio - la "vita" e la "scuola")
    vedi.

Problema 4. (correlaz. non condondere correlazione statistica con relazione "causa-effetto")
    vedi.

Problema 5. (non tutto è gaussiano)
    vedi   (leggi anche gli "altri commenti").

Problema 6. (come "definire" la probabiità")
    vedi.

Le proprietà della probabilità sono sostanzialmente le stesse delle frequenze percentuali e (a parte la limitazione superiore ad 1 dei valori assumibili) delle misure di superfici: da questo punto di vista non c'è nulla di nuovo (vedi qui per una presentazione di questi aspetti rivolta agli alunni di 2ª superiore)

[Il problema 6 era riferito alla introduzione del concetto di probabilità.  Altra questione è l'introduzione del concetto di "evento".  Secondo me, a scuola, le variabili casuali devono essere considerate delle variabili "speciali" piuttosto che dei "complicati" insiemi, e analogamente gli eventi devono essere considerati delle condizioni piuttosto che degli insiemi.  Le motivazioni sono varie: vedi (sono le stesse per cui in gran parte dei manuali statistici universitari - e, almeno negli Stati Uniti, anche dei manuali universitari di "probabilità e statistica" - sono introdotte in questo modo!).  Per l'impostazione scelta nel progetto MaCoSa: vedi]

# Come realizzare alcune delle immagini riportate e delle elaborazioni proposte con R
source("http://macosa.dima.unige.it/r.R")
#
SQUARES(8,10)
COUNT(10)
for(i in c(1,3,4,7,8,10)) CROSS(3,i)
for(i in c(3,5,7)) CROSS(5,i)
for(i in c(1,4,5,7)) CROSS(7,i)
for(i in c(2,5,6,9)) CIRCLE(3,i)
for(i in c(1,2,4,6)) CIRCLE(5,i)
for(i in c(2,3,6,8)) CIRCLE(7,i)
LCROSS(3,"Piedi"); LCROSS(5,"Auto"); LCROSS(7,"Bus")
#
SQUARES(10,6)
COUNT(6)
for(i in 1:4) for(j in 3:5) CIRCLE(j,i)
for(i in 1:6) CROSS(7,i)
for(i in 1:3) CROSS(8,i)
for(i in 1:4) CROSS(9,i)
LCROSS(3,"P"); LCROSS(4,"A"); LCROSS(5,"B")
LCROSS(7,"P"); LCROSS(8,"A"); LCROSS(9,"B")
--------
arrivi = c(25, 10, 9.4, 12.1, 7.3, 4.2, 31.9)
giorni = c(30.9, 10.4, 3.0, 4.1, 4.1, 1.1, 31.9)
nomi = c("D","CH","F","US","UK","E","al")
nomiTorta=nomi; torta(arrivi)
# giallo,celeste,... % 25.02503 10.01001 9.409409 12.11211 7.307307 4.204204 31.93193 
# giallo,celeste,... D CH F US UK E al 
nomiBarre=nomi; Barre(giorni)
# giallo,celeste,... % 36.14035 12.16374 3.508772 4.795322 4.795322 1.28655 37.30994 
---------
giorni <- seq(1,31,1)
C1 <- c(3,4,5,2,2,3,4,5,6,8,8,9,10,10,8,7,8,6,4,5,4,6,5,7,6,9,12,11,14,11,12)
C2 <- c(3,4,6,2,2,3,4,6,6,8,9,9,8,10,8,7,8,6,4,1,2,3,5,7,6,9,12,11,14,13,13)
max(c(C1,C2))
# 14
## Le temperature in funzione del tempo
Piano(0,31, 0,14)
spezzata(giorni,C1,"red"); PUNTO(giorni,C1,"blue")
Piano(0,31, 0,14)
spezzata(giorni,C2,"red"); PUNTO(giorni,C2,"blue")
## Gli istogrammi con le frequenze assolute
nomi=c("0-2","3-5","6-8","9-11","12-14")
nomiBarre=nomi; BARRE( c(2,10,10,6,3) )
nomiBarre=nomi; BARRE( c(4,7,11,5,4) )
---------
carne = c(83, 524, 211)
nomiBarre = c("bov","sui","ovi")
Barre(carne)
# giallo,celeste,... % 10.1467 64.05868 25.79462 
Striscia(carne)
# giallo,celeste,... % 10.1467 64.05868 25.79462 
--------
dati <- c(64,66,73,86,70,75,68,86,88,63,73,70,69,66,77,80,
     80,77,82,61,77,71,59,84,86,70,77,70,97,68,66,70,70,68,
     70,68,81,73,61,73,59,70,68,67,70,68,64,82,86,66,68,74,
     64,64,62,56,70)
stem(dati)

-------
freq <- c(729,35,77,132,134,285,457,1401,1569); BarC(freq,"grey")
 
-------
SUC <- function(i) ifelse(i==3,1,i+1)

Event = function() {
 V = 0; x = NULL; y = NULL; Lato = 8; Diam = 1; L = Lato-Diam
 for(i in 1:3) { x[i] = runif(1)*L+1/2; y[i] = runif(1)*L+1/2 }; i=1
 while(i<=3) { j=SUC(i); k=SUC(j); d=point_line(x[i],y[i], x[j],y[j],x[k],y[k]); 
               i=i+1; if(d < Diam) {V = 1; i = 4} }; x <<- x; y <<- y; V }

genera = function() {
  polyC(c(0,8,8,0),c(0,0,8,8),"yellow")
  n = ifelse(Event(),1,0)
  text(0.5,0.5,n); text(7.5,7.5,n); text(0.5,7.5,n); text(7.5,0.5,n)
  for(i in 1:3) {circleC(x[i],y[i], 1/2, "white");circl(x[i],y[i], 1/2, "blue")}
  polyC(x,y, 0);  }

rowcol(3,5); for(i in 1:15) {BoxmW(0,8, 0,8); genera()}


# ----------
PR = function(n) {f = 0; for (i in 1:n) f = f + ifelse(Event(),1,0);
       fr = f/n; S = sqrt(fr*(1-fr)/(n-1)); cat(fr*100, "+/-", 3*S*100,'\n') }

n=10000; cat(n,"  "); PR(n)
n=n*4; cat(n,"  "); PR(n)
# 
# ...
# n=n*4; cat(n,"\t"); PR(n)
# 10240000   42.05155 +/- 0.04629099