Attività con R - 1
[righe da eseguire, tra un "#" e l'altro]

1/3
print(1/3, 15); print(1/3, 16); print(1/3, 17); print(1/3, 18)
# come mai queste uscite?
x <- 5555.1251; y <- 5555; x-y
print(x-y, 16)
# come mai queste?
# Col cellulare 1/3*3 fa 0.9999999
13/124+4/80
library(MASS)
# che cos'è una "libreria"
fractions(13/124+4/80)
fractions(1255.255255255255255255)
fractions( 2.59807621135332/sqrt(3) )
# Deduco che 2.59807621135332 = 3√3/2
3+sqrt(-0.25)
# NAN: not a number
3+sqrt(-0.25+0i)
# i numeri complessi
#
as.roman(178); as.roman(179); as.roman(999)
# Only numbers between 1 and 3899 have a representation as roman numbers
#
factorial(21)
fractions(factorial(21))
fractions(factorial(22))
# come effettuare il "calcolo esatto"
#
# http://www.wolframalpha.com
# 2.59807621135332
# sqrt(3)/2
# 13/124+4/80
# 3+sqrt(-0.25)
# Is 5^(1/3) a rational number?
# Is pi^sqrt(2) a rational number?
# roman(999)
# 22!
#
c( choose(7,0), choose(7,1), choose(7,2), choose(7,3) )
choose(7,0:7)
# il ":"
#
2 < 5; 5 >= 2; 5 == 2; 5 = 2
!(1 > 2 & (3/2 < 2 | 1 == 0))
1 > 2 & (3/2 < 2 | 1 == 0)
1 > 2
3/2 < 2 | 1 == 0
3/2 < 2
1 == 0
# gli operatori "logici" e l'"=" nelle condizioni
#
k <-2; t <- 1
p <- function(x) (x^2+x+1)^2 + 1/(x^2+x+1) + x^2+x+1
q <- function(x) {t <- x^2+x+1; t^k + 1/t + t}
p(7); q(7)
t; k
# nella definizione di q ho usato la variabile t come variabile locale (il
# valore che assume non interferisce col valore che t ha assunto prima della
# definizione, in cui era globale, come globale è la varabile k); x è invece
# un parametro formale (è usato per definire q; anch'esso non interferisce
# coi valori assunti da eventuali usi di x al di fuori della definizione di q)
#
f <- function(x) ifelse( x>= 2, -4, 6)
plot(f,-5,5); abline(h=0,v=0,col="red")
#
plot(f,-5,5,type="p"); abline(h=0,v=0,col="red")
#
plot(f,-5,5,type="p",pch="."); abline(h=0,v=0,col="red")
#
plot(f,-5,5,type="p",pch=".",n=1e4); abline(h=0,v=0,col="red")
#
# http://www.wolframalpha.com
# y = Piecewise[ { {-4, x >= -2}, {6, x < -2} } ]
# Per avere il grafico in un particolare intervallo:
# plot Piecewise[ { {-4, x >= -2}, {6, x < -2} } ], -8 <= x <= 8
# ovvero:
# plot Piecewise[ { {-4, x >= -2}, {6, x < -2} } ], -8 <= x <= 8, -7 <= y <= 9
#
readLines("http://macosa.dima.unige.it/om/prg/stf/altomas.txt",n=3)
# vedo che cos'è un file, stampandone poche righe,
read.table("http://macosa.dima.unige.it/om/prg/stf/altomas.txt",sep=",",skip=1, nrows=2)
# poi, se vedo che è una tabella, ne carico le righe indicando il separatore
hm <- read.table("http://macosa.dima.unige.it/om/prg/stf/altomas.txt",sep=",",skip=1)
str(hm)
#
edit(hm)
#
hm
write.csv(hm,"hm.csv")
# come scrivere una tabella in formato foglio di calcolo
# (cercare il file sul computer: potrebbe essere nella cartella
#  Documenti, sul DeskTop, ...)
#
plot(hm)
hf <- read.table("http://macosa.dima.unige.it/om/prg/stf/altofem.txt",sep=",",skip=1)
windows() # apro una nuova finestra
plot(hf)
#
plot(hf,ylim=c(160,250),col="red")
abline(v=axTicks(1), h=axTicks(2), col="orange",lty=3)
points(hm,col="blue")
lines(hm,col="blue"); lines(hf,col="red")
#
indm <- hm$V2/hm$V2[1]*100; indf <- hf$V2/hf$V2[1]*100
# estraggo righe/colonne da una tabella
plot(hf$V1,indf,col="red")
abline(v=axTicks(1), h=axTicks(2), col="orange",lty=3)
points(hm$V1,indm,col="blue")
lines(hm$V1,indm,col="blue")
lines(hf$V1,indf,col="red")
#
ls()
rm(hm,t)
ls()
rm(list=ls())
ls()
# come vedere le variabili definite, come cancellarne alcune o tutte
#
x <- c(10.4, 5.6, 3.1, 6.4, 21.7); x
length(x); min(x); max(x); range(x); sort(x); mean(x); median(x); sum(x); prod(x)
#
seq(3,10,len=4); seq(6,10,0.5)
length(seq(6,10,0.5))
# un modo per costruire sequanze
#
dati <- c(315.5, 732.3, 586.7); barplot(dati)
# un istogramma a barre
# come aggiungervi delle etichette:
windows()
names(dati) <- c("nord","centro","sud"); barplot(dati)
windows()
barplot(dati/sum(dati)*100)
abline(h=axTicks(2), col="blue",lty=3)
windows()
barplot(dati/sum(dati)*100,horiz=TRUE)
abline(v=axTicks(1), col="blue",lty=3)
windows()
# come orientare le "etichette" sugli assi
barplot(dati/sum(dati)*100,horiz=TRUE,las=1)
abline(h=axTicks(2), col="blue",lty=3)
#
# Come cercare queste cose nell'indice per voci
# Esempi d'uso di WolframAlpha: apri "software" qui
# (poi apri "clicca").
# Per come vengono approssimati i numeri, vedi qui.
# Domande, problemi, ... ?
#
# (vedremo una prossima volta come salvare/caricare sessioni di lavoro)
#

Attività con R - 2

# Schiacciando il tasto freccia ^ [v] si rivedono preced. [segu.] comandi.
# Quanto fatto può essere memorizzato usando il comando Save History
# e dandogli un nome (con estensione ".Rhistory"). Il file può essere
# ricaricato con Load History e può essere esaminato o caricato con i
# tasti freccia, come detto sopra.
#
# Per esamiare alcune funzioni incorporate si puo' guardare uno dei vari
# help; ad es. selezionare "R functions (text)" [o "Funzioni di R (testo)],
# mettere "sqrt" come parola da cercare; si apre "MathFun {base}" e da qui
# si seleziona "Math".  Si può usare anche "Search Engine & Keywords"
# attivabile da "Html Help" ("Guida Html"), e, soprattutto, sempre da
# "Html Help", aprire "Packages" e, quindi, "Base" e "Graphics".
# Si tratta, comunque, di help non "facili".     Battendo il comando
# help(sqrt)  si entra direttamente nell'help di sqrt (se non sei in rete
# potrebbe essere azionabile solo "Search Help" - "Cerca nella Guida").
#
# I grafici di tre funzioni a 1 input e 1 output con curve (con cui non è
# necessario - ma è possibile - specificare il dominio) e l'opzione add (ci
# sono anche altri modi per ottenerli) e plot (qui solo) per scegliere la scala:
# la 2ª riga riserva lo spazio per il rettangolo con ascissa da -5 a 5 e
# ordinata da -5 ad 8 e non lo traccia (type="n"), e non mette etichette agli
# assi (xlab="", ylab=""); con fg="white" non traccio il box, con xaxt="n",
# yaxt="n" ascisse/ordinate. I comandi sono copiabili facilmente e modificabili.
f <- function(x) x*2-1; g <- function(x) x^2-1; h <- function(x) x/2-1
plot(c(-5,5),c(-5,8),type="n",xlab="", ylab="")
abline(h=0,v=0,col="brown"); abline(v=axTicks(1), h=axTicks(2), col="brown",lty=3)
curve(f, add=TRUE,col="red"); curve(g, add=TRUE,col="blue"); curve(h,add=TRUE)
#
plot(c(-5,5),c(-5,8),type="n",xlab="", ylab="",fg="white")
abline(h=0,v=0,col="brown"); abline(v=axTicks(1), h=axTicks(2), col="brown",lty=3)
#
plot(c(-5,5),c(-5,8),type="n",xlab="", ylab="",fg="white",xaxt="n",yaxt="n")
abline(h=0,v=0,col="brown"); abline(v=axTicks(1), h=axTicks(2), col="brown",lty=3)
#
# Una definizione per ricorsione:
A <- 90000
F <- function(n) if (n==0) 1 else (Recall(n-1)+A/Recall(n-1))/2
# ovvero: F <- function(n) if (n==1) 1 else (Recall(n-1)+A/Recall(n-1))/2
F(1); F(2); F(10); F(11); F(12)
A <- 1024; F(9); F(10)
# Che cosa calcola F?
# x(0)=1, x(n+1) = ( x(n) + A/x(n) ) / 2 (che converge a ...)
#
# Se un comando e' lungo si puo' scriverlo tutto su una stessa riga fino
# a qualche migliaio di caratteri o si puo' andare a capo: la riga seguente
# è interpretata come continuazione (sullo schermo è aggiunto automaticamente
# un "+" all'inizio della nuova riga). Un esempio:
dati <- c(1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,
         21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40)
mean(dati)
#
# generazione di alcune sequenze di numeri interi:
s <- 5:11; s; 5:11-1; 5:(11-1); 11:5; s/2
# più in generale:
seq(6); seq(3,9); seq(3,10,0.8); seq(3,10,len=4); seq(3,by=0.8,len=6)
# modi per ripetere più volte dei dati:
x <- c(3.1, 6.4, 21.7); c(7,rep(x, 4)); c(7,rep(x, each=4))
#
# analisi dei dati relativi ad un gruppo di alunne quindicenni (altezze in cm)
alu <- c(156,168,162,150,167,157,170,157,159,164,157,165,163,165,166,160,163,162,155)
length(alu); sort(alu); mean(alu); median(alu)
# Stem-and-leaf plot (o, in breve, stem plot). La cifra indicata nella
# prima colonna è il "gambo" (stem) del singolo dato, la cifra rimanente
# è la "foglia" (leaf); per ogni gambo ci possono essere più foglie
# (dati classificati nella stessa classe).
stem(alu)
# un modo per contare le lunghezze delle colonne, anche parziali
stem(alu, width = 0); stem(alu, width = 2)
# come scegliere intervalli diversi (lo standard equivale a scale=1)
stem(alu,scale=0.5); stem(alu,scale=3)
#

Si può dimostrare che la successione  A(0)=1, A(n+1) = (A(n) + k/A(n)) / 2, con k > 0, convege a √k. Questo è un efficientissimo algoritmo per calcolare la radice quadrata di un numero che risale agli antichi babilonesi. Ha come idea originale la seguente osservazione: se A è una approssimazione per eccesso [difetto] di √k allora k/A ne è una approssimazione per difetto [eccesso] (da A > √k segue che k/A < √k), e quindi come migliore approssimazione si può prendere la media artitmetica, (A+k/A)/2, di tali approssimazioni.
 

Attività con R - 3

# Riprendiamo la
# analisi dei dati relativi ad un gruppo di alunne quindicenni (altezze in cm)
alu <- c(156,168,162,150,167,157,170,157,159,164,157,165,163,165,166,160,163,162,155)
length(alu); min(alu); max(alu); mean(alu); median(alu)
# abbiamo visto come, col comando scale (con un numero maggiore o minore di 1)
# si possono ottenere diversi "stem-and-leaf" plot
stem(alu,scale=3); stem(alu)
#
# Vediamo, ora, come ottenere istogrammi più articolati.
# Con seq (scelto un certo intervallo (da 140 a 180) e l'ampiezza (5) delle
# classi in cui suddividerlo) decido se classificare i dati in intervalli del
# tipo [.,.) - right=FALSE - come fa automaticamente lo stem, o del tipo
# (.,.] - right=TRUE (noi sceglieremo sempre il 1º tipo):
hist(alu, seq(140,180,5), right=FALSE)
windows(); hist(alu, seq(140,180,5), right=TRUE)
# Ho fatto gli istogrammi in due finestre diverse, che posso spostare o
# ridimensionare. Chiudiamole entrambe cliccando [x].
#
# Ecco l'istogramma in intervalli di altra ampiezza, colorato, senza scritte
# (con main posso inserire un titolo alternativo, anche 'vuoto'):
hist(alu,seq(150,171,3),right=FALSE,col="yellow",xlab="",ylab="",main="")
#
# Posso ridurre il margine dei grafici usando il comando par (PARametri grafici)
# con l'opzione mai (MArgini Interni, in pollici). Posso far gestire al software
# l'istogramma specificando con nclass più o meno in quanti intervalli
# classificare i dati [viene scelto un n. di classi tale che esse siano ampie 1,
# 2 o 5 volte una potenza di 10]:
par( mai = c(0.5,0.5,0.1,0.1) )
hist(alu,nclass=8,right=FALSE,col="yellow",xlab="",main="")
#
# Aggiungendo l'opzione  probability=TRUE (o freq=FALSE) posso rappresentare le
# densità, ossia il rapporto tra le frequenze e le ampiezze delle classi:
hist(alu,nclass=8,right=FALSE,col="yellow",xlab="",main="",probability=TRUE)
#
# Posso far tracciare anche l'istogramma in classi di diverse ampiezze (sulla
# scala verticale appare la densità; perché?); devo scegliere in ogni caso
# l'ultimo estremo maggiore strettamente del massimo (170 nel nostro caso)
# per avere un istogramma "corretto".
hist(alu,c(150,156,159,162,168,171),right=FALSE,xlab="",main="")
#
# Ritorneremo, la prossima volta, su quali strumenti utlilizzare per analizzare
# dati come questi. Ora vediamo l'uso di runif, il generatore di numeri
# (pseudo)casuali
runif(1); runif(1); runif(1)
#
# vengono generati numeri con valori "casuali" tra 0 ed 1 (che sono
# uniformemente distribuiti, ossia che tendono ad avere la stessa frequenza
# in sottointervalli di eguale ampiezza; tra 0 e 1/3 e tra 2/3 ed 1 abbiamo
# percentuali di uscite che tendono ad eguagliarsi).
# Con runif posso ottenere altri valori casuali, ad es. relativi al lancio
# di un dado (floor è la parte intera):
floor(runif(1)*6)+1; floor(runif(1)*6)+1; floor(runif(1)*6)+1
#
# Opzioni: runif(7) o runif(3,min=1,max=7) generano 7 "numeri casuali" tra
# 0 ed 1 o 3 tra 1 e 7. Ecco come ottenere 25 lanci di un dado equo:
floor(runif(25,min=1,max=7))
#
# Come faccio a controllare che runif generi uscite uniformemente distribuite?
# Con il seguente comando posso vedere, graficamente, come di distribuiscono
# 1000 uscite di runif
hist(runif(1000))
#
# Se voglio avere le frequenze relative uso il segunte comando, eventualmente
# con probability=TRUE al posto di freq=FALSE
hist(runif(1000),freq=FALSE)
# posso specificare il numero di intervalli:
hist(runif(1000),probability=TRUE,nclass=2)
#
# All'aumentare il numero delle prove l'istogramma tende ad appiattirsi
hist(runif(1e4),probability=TRUE,nclass=2)
#
# ma se aumento il numero delle classi ...
hist(runif(1e4),probability=TRUE,nclass=100)
#
# devo aumnetare il numero delle uscite
hist(runif(1e6),probability=TRUE,nclass=100)
# Approfondiremo più avanti la riflessione su come "tende" ad appiattirsi
#
# Non basta vedere che le uscite di runif tendono ad essere distribuite
# uniformemente. Basti osservare le seguenti uscite:
n <- 8; x <- runif(n); x
i <- seq(4,n,4); x[i] <- x[i-2]; x
# Si susseguono, via via, coppie di elementi uguali. Ma se li analizzo con
# un istogramma non mi accorgo di questo fatto:
n <- 1e5; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
hist(x)
# È evidente come la simulazione di un fenomeno con un generatore di
# numeri casuali di questo tipo potrebbe creare grossi problemi.
# Non abbiamo, per ora gli strumenti per mettere a punto come "testare" un
# generatore di numeri casuali. Ci rifletteremo eventualmente più avanti.
#
# Per renderci conto della bontà di runif vediamo solo come di distribuiscono
# coppie di punti con coordinate generate esso. Che cosa ci aspettiamo?
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
points(runif(1000),runif(1000))
#
# Se voglio aumentare il numero dei punti mi conviene tracciarli puntiformi
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
points(runif(1000),runif(1000),pch=".")
#
# A questo punto posso aumentare il numero dei punti tracciati:
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
n <- 1e4; points(runif(n),runif(n),pch=".")
#
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
n <- 1e5; points(runif(n),runif(n),pch=".")
#
# Ma, come fanno ad essere casuali le uscite generate da un computer?
# Ci rifletteremo su la prossima volta.
#

Attività con R - 4

# PARENTESI - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Che cos'è una successione casuale? Una possibile definizione (Chaitin, 1962).
#             (spiegazione e definizione a livello "adulto")
#
# Idea intuitiva: una sequenza finita di caratteri è più "casuale" di un'altra di
# uguale lunghezza se può essere descritta in un modo più breve di questa.
# Fissato un linguaggio di programmazione, data una stringa finita di caratteri w
# chiamo complessità di w, e indico con C(w), la lunghezza minima di un programma
# che generi w.
# Esempio, in R ('noquote' toglie le virgolette):
w <- "abcdeabcde"
noquote("abcdeabcde")
# stringa lunga len(w) = 10, complessità 11+10 = 21 (devo solo togliere le virgolette)
# Sicuramente ogni stringa finita w ha C(w) <= len(w)+11.
# Vediamo cosa accade per:
w <- "abcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcde"
#     123456789A123456789B123456789C123456789D123456789E123456789F123456789G123456789H
# len(w) = 80; C(w) è strettamenete inferiore di len(w)+11, cioè di 91
# Posso infatti generare la stringa in forma "compressa" con i comandi seguenti, dove
# "paste" incolla due stringhe con un certo separatore (qui senza alcun separatore):
w<-""; for(n in 1:16) w<-paste(w,"abcde",sep=""); noquote(w)
#23456789A123456789B123456789C123456789D123456789E123456789F
# C(w) al più è 60 (< len(w)).
#
# Posso pensare che una stringa infinita sia casuale se non è comprimibile. Precisiamo
# che cosa possiamo intendere per "comprimibile" nel caso infinito.
# Idea: una stringa infinita S è comprimibile se le sue sottostringhe w abbastanza
# grandi hanno C(w) che tende ad essere via via più piccola di len(w). Dunque:
# una stringa infinita S è casuale se l'insieme {len(w)-C(w) / w sottostringa di S}
# è limitato superiormente.
#
# Questa è l'idea della definizione, che può essere estesa a considerare
# successioni di altri oggetti matematici.
#
# La successione delle cifre di un numero irrazionale è casuale? Se è generabile
# con un algoritmo, no!  Tuttavia i numeri reali generabili con un algoritmo (ovvero
# di cui posso conoscere, potenzialmente, tutte le cifre che voglio) sono una infinità
# numerabile, essendo tale la quantità dei programmi che si posso descrivere con un
# linguaggio formale: la conoscenza delle cifre della stragrande maggioranza dei
# numeri reali non è alla nostra portata.
#
# Si può dimostrare (teorema di incompletezza di Chaitin-Gödel) che non è possibile
# dimostrare che una successione infinita di caratteri è casuale.
#
# Questo risultato è una versione "generale" del Teorema di Incompletezza a cui
# accennerete nel corso di Logica; esso esprime in modo molto generale i limiti
# intrinseci dei sistemi formali.
# FINE PARENTESI - - - - - - - - - - - - - - - - - - - - - - - - - -
#
# Pur essendo giunti alla conclusione che non è possibile dimostrare la casualità di
# una successione, nella realtà interessa costruire degli algoritmi per generare
# successioni che, ai fini pratici, si comportino come se fossero "casuali". Questo
# servirà, in particolare, per simulare e studiare statisticamente fenomeni casuali.
#
# Dopo vari insuccessi, sono stati messi a punto vari generatori di successioni
# (pseudo)casuali di numeri. Attualmente i più usati sono basati sullo schema noto
# come metodo congruenziale lineare:  X(n+1) = (a*X(n)+c) mod M  (a,X(0),c,M numeri
# naturali; a,X(0),c < M) o su schemi simili:  X(n) = (a*X(n-h)−b*X(n-k)) mod M
# (dove tutte le costanti sono numeri naturali fissati).
# Si genera in tal modo una sequenza di numeri interi compresi tra 0 e M, da cui si
# può ottenere una sequenza di numeri in [0,1) dividendo ciascuno di essi per M.
#
# Scegliendo opportunamente le costanti si può verificare, attraverso test statistici,
# che tale successione si comporta, apparentemente (non realmente: è generata con un
# algoritmo!), in modo "massimamente" casuale. I test riguardano l'uniformità della
# distribuzione, l'indipendenza di ogni uscita dalle precedenti (o, meglio, da alcune
# centinaia delle precedenti - 623 nel caso di quello standard di R: da tutte non può
# esserlo!) e molti altri aspetti.
# Vediamo quale generatore usa R: cerchiamo nella "guida Html" del programma la voce
# Random Number Generation; il generatore usato normalmente da R è quello chiamato
# Mersenne-Twister, ideato nel 1998, che ha un periodo lungo 2^19937 - 1. Non ci
# preoccupiamo di esaminare nel dettaglio come esso opera (chi vuole può recuperare
# dal sito come accedere a tali informazioni).
#
# Vediamo solo qualche esempio di generatori di numeri casuali. L'obiettivo è dare
# un'idea di come sia complesso il fenomeno, e pensare come, volendo, si possa far
# percepire questa complessità ai ragazzi.
# In alcuni di questi generatori compare il simbolo funzionale %% che rappresenta
# (in R e in molti linguaggi di programmazione) la funzione mod:(M,N) -> "resto
# intero della divisione di M per N"
#
## LungRnd0
# Consideriamo il "generatore" seguente (parto da x0 e ottengo via via gli altri
# numeri applicando Rand):
a <- 7; M <- 100; c <- 70; x0 <- 60
Rand <- function(x) (a*x+c) %% M
# Vediamo qualche esempio d'uso:
Rand(60)
# ottengo 90
Rand(90)
# 0
Rand(0)
# 70
Rand(70)
# 60
# Ho riottenuto 60, dopo solo 4 uscite, con 4 molto più piccolo di M (100).
# Vediamo come avrei potuto procedere senza fare uno ad uno i tentativi: conto con n
# le prove e le ripeto fino a che riottengo x0:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# riottengo ottengo 4.
# Questo era un brutto generatore. Dà un'idea di come non si possa procedere a caso.
# Proviamo con un'altro.
#
## LungRnd1
# Generatore che era stato proposto in: "Le scienze con il calcolatore tascabile"
# (R.Green, J.Lewis - Muzzio Editore - 1980)
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
# Proviamo direttamente a trovare il periodo:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# ottengo 16384.
# È un valor molto grande (=65536/4). Potrei usarlo questo generatore per simulare
# qualche semplice fenomento. Dovrò verificare che la distribuzione sia accettabile
# come uniforme. Come abbiamo detto la cosa non è facile. Proviamo, solo, a vederlo
# graficamente, nel modo seguente (prima "normalizziamo" le uscite, ossia le
# trasformiamo in numeri tra 0 ed 1 dividendole per M).
# Idea: genere a caso una x, memorizzarne il valore come u, proseguire generando un'altra
# x e rapresentare il punto u/m ed x/M.
#
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
x <- x0
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
...

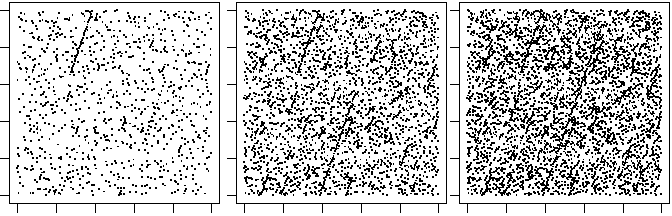# Hanno un comportamento simile i generatori casuali impiegati nei personal computer
# nella prima metà degli anni '80. Bastano queste uscite grafiche per rendersi
# conto dei limiti di questi generatori.
#
# Per mettere in luce l'opportunità di altri metodi esaminiamo un altro generatore
# che fu molto impiegato.
#
## LungRnd2
# Generatore proposto nel manuale del pocket computer HP-25 (più o meno
# contemporaneo al precedente).
# Genera direttamente numeri tra 0 ed 1 (genera numeri x e ne prende la parte
# frazionaria con x-"parte intera di x")
R0 <- 1/2
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
# Proviamo ad usarlo:
R <- 1/2
R <- Rand(R); R
# 0.4081073
R <- Rand(R); R
# 0.5834226
#
# Proviamo a trovarne il periodo:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
while(alt == 0) if(Rand(R)==R0) {print(n); alt <- 1} else {R <- Rand(R); n <- n+1}
# non si ferma: lo fermo io (con ESC) e stampo n ed R. Ottengo per esempio:
n; R
# 116734    0.5740558
#
# Le uscite sono numeri decimali di parecchie cifre; non abbiamo più
# valori interi come prima, che ciclavano, Questo è un generatore di tipo
# diverso.
# Esaminiamo le ucite graficamente:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
...

...
# Le uscite sembrano disporsi uniformente. Ma questa è solo un'impressione.
# Proviamo a verifcarlo anche con un istogramma:
R <- 1/2; u <- NULL; for(i in 1:1e4) {u <- c(u,R); R <- Rand(R)}
hist(u,freq=FALSE)

# L'istogramma sembra confermarci la cosa.
# Questa verifica non è tuttavia sufficiente.
#
# Ad esempio anche per il generatore di numeri casuali visto alla fine della
# volta scorsa, evidentemente "non del tutto casuale" (si ripetono coppie di
# uscite uguali), di cui abbiamo già visto la forma "piatta" dell'istogramma:
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]; hist(x,freq=FALSE)

# basandosi su queste prove non si hanno indizi della sua "non bontà":
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x1 <- x
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x2 <- x
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
points(x1,x2,pch=".")

# In questo caso, sapendo come è costruito questo "generatore", possiamo
# costruire una verifica che ne mette in luce i limiti.
# Ecco che cosa si ottiene studiando statisticamente  (1) i valori ottenuti
# facendo le differenze tra il valore ottenuto col generatore standard e
# quello ottenuto due uscite prima (mi aspettio una distribuzione triangolare:
# il valore più frequente è 0, e poi via via, andando verso -1 ed 1, le
# frequenze diminuiscono) e  (2) quelli ottenuti analogamente con questo
# generatore (uno ogni due valori viene 0: la differenza tra due numeri
# uguali):
n <- 1e4; y <- runif(n)
i <- 1:(n-2); w <- NULL; w[i] <- y[i+2]-y[i]
hist(w,freq=FALSE,seq(-1,1,2/15))
#
x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
i <- 1:(n-2); z <- NULL; z[i] <- x[i+2]-x[i]
hist(z,freq=FALSE,seq(-1,1,2/15))

#
# Ci siamo resi conto della complessità dell'argomento. Averlo un po'
# maneggiato ci ha dato un'idea di quanta "matematica" ci sia dietro alla
# messa a punto di uno strumento apparentemente semplice come questo.
#
# Un'ultima osservazione: queste successioni (LungRnd1, LungRnd2) possono
# partire prendendo come valore inziale invece del valore x0 indicato un
# altro valore tra quelli generati. Lo stesso accade per runif.
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa
# partire la successione "casuale" da un dato valore (con lo stesso n ho
# la stessa sequenza)
set.seed(7); runif(3); runif(3)
# 0.9889093 0.3977455 0.1156978
# 0.06974868 0.24374939 0.79201043
set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978;  ho riottenuto gli stessi valori:
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo
# in molte situazioni (testare un algoritmo sulla stessa successione di valori,
# controllare simulazioni di fenomeni, memorizzare codifiche segrete, ...).
#
# Accanto a questi "pseudo generatori di numeri casuali" (PRNG) vi sono anche
# degli "hardware random number generator" generati da un processo fisico,
# basati su fenomeni termici, fotoelettrici, quantistici, utilizzati per
# particolari applicazioni, non in ambito statistico.
#