Attività con R - 4
# PARENTESI - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Che cos'è una successione casuale? Una possibile definizione (Chaitin, 1962).
# (spiegazione e definizione a livello "adulto")
#
# Idea intuitiva: una sequenza finita di caratteri è più "casuale" di un'altra di
# uguale lunghezza se può essere descritta in un modo più breve di questa.
# Fissato un linguaggio di programmazione, data una stringa finita di caratteri w
# chiamo complessità di w, e indico con C(w), la lunghezza minima di un programma
# che generi w.
# Esempio, in R ('noquote' toglie le virgolette):
w <- "abcdeabcde"
noquote("abcdeabcde")
# stringa lunga len(w) = 10, complessità 11+10 = 21 (devo solo togliere le virgolette)
# Sicuramente ogni stringa finita w ha C(w) <= len(w)+11.
# Vediamo cosa accade per:
w <- "abcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcdeabcde"
# 123456789A123456789B123456789C123456789D123456789E123456789F123456789G123456789H
# len(w) = 80; C(w) è strettamenete inferiore di len(w)+11, cioè di 91
# Posso infatti generare la stringa in forma "compressa" con i comandi seguenti, dove
# "paste" incolla due stringhe con un certo separatore (qui senza alcun separatore):
w<-""; for(n in 1:16) w<-paste(w,"abcde",sep=""); noquote(w)
#23456789A123456789B123456789C123456789D123456789E123456789F
# C(w) al più è 60 (< len(w)).
#
# Posso pensare che una stringa infinita sia casuale se non è comprimibile. Precisiamo
# che cosa possiamo intendere per "comprimibile" nel caso infinito.
# Idea: una stringa infinita S è comprimibile se le sue sottostringhe w abbastanza
# grandi hanno C(w) che tende ad essere via via più piccola di len(w). Dunque:
# una stringa infinita S è casuale se l'insieme {len(w)-C(w) / w sottostringa di S}
# è limitato superiormente.
#
# Questa è l'idea della definizione, che può essere estesa a considerare
# successioni di altri oggetti matematici.
#
# La successione delle cifre di un numero irrazionale è casuale? Se è generabile
# con un algoritmo, no! Tuttavia i numeri reali generabili con un algoritmo (ovvero
# di cui posso conoscere, potenzialmente, tutte le cifre che voglio) sono una infinità
# numerabile, essendo tale la quantità dei programmi che si posso descrivere con un
# linguaggio formale: la conoscenza delle cifre della stragrande maggioranza dei
# numeri reali non è alla nostra portata.
#
# Si può dimostrare (teorema di incompletezza di Chaitin-Gödel) che non è possibile
# dimostrare che una successione infinita di caratteri è casuale.
#
# Questo risultato è una versione "generale" del Teorema di Incompletezza a cui
# accennerete nel corso di Logica; esso esprime in modo molto generale i limiti
# intrinseci dei sistemi formali.
# FINE PARENTESI - - - - - - - - - - - - - - - - - - - - - - - - - -
#
# Pur essendo giunti alla conclusione che non è possibile dimostrare la casualità di
# una successione, nella realtà interessa costruire degli algoritmi per generare
# successioni che, ai fini pratici, si comportino come se fossero "casuali". Questo
# servirà, in particolare, per simulare e studiare statisticamente fenomeni casuali.
#
# Dopo vari insuccessi, sono stati messi a punto vari generatori di successioni
# (pseudo)casuali di numeri. Attualmente i più usati sono basati sullo schema noto
# come metodo congruenziale lineare: X(n+1) = (a*X(n)+c) mod M (a,X(0),c,M numeri
# naturali; a,X(0),c < M) o su schemi simili: X(n) = (a*X(n-h)−b*X(n-k)) mod M
# (dove tutte le costanti sono numeri naturali fissati).
# Si genera in tal modo una sequenza di numeri interi compresi tra 0 e M, da cui si
# può ottenere una sequenza di numeri in [0,1) dividendo ciascuno di essi per M.
#
# Scegliendo opportunamente le costanti si può verificare, attraverso test statistici,
# che tale successione si comporta, apparentemente (non realmente: è generata con un
# algoritmo!), in modo "massimamente" casuale. I test riguardano l'uniformità della
# distribuzione, l'indipendenza di ogni uscita dalle precedenti (o, meglio, da alcune
# centinaia delle precedenti - 623 nel caso di quello standard di R: da tutte non può
# esserlo!) e molti altri aspetti.
# Vediamo quale generatore usa R: cerchiamo nella "guida Html" del programma la voce
# Random Number Generation; il generatore usato normalmente da R è quello chiamato
# Mersenne-Twister, ideato nel 1998, che ha un periodo lungo 2^19937 - 1. Non ci
# preoccupiamo di esaminare nel dettaglio come esso opera (chi vuole può recuperare
# dal sito come accedere a tali informazioni).
#
# Vediamo solo qualche esempio di generatori di numeri casuali. L'obiettivo è dare
# un'idea di come sia complesso il fenomeno, e pensare come, volendo, si possa far
# percepire questa complessità ai ragazzi.
# In alcuni di questi generatori compare il simbolo funzionale %% che rappresenta
# (in R e in molti linguaggi di programmazione) la funzione mod:(M,N) -> "resto
# intero della divisione di M per N"
#
## LungRnd0
# Consideriamo il "generatore" seguente (parto da x0 e ottengo via via gli altri
# numeri applicando Rand):
a <- 7; M <- 100; c <- 70; x0 <- 60
Rand <- function(x) (a*x+c) %% M
# Vediamo qualche esempio d'uso:
Rand(60)
# ottengo 90
Rand(90)
# 0
Rand(0)
# 70
Rand(70)
# 60
# Ho riottenuto 60, dopo solo 4 uscite, con 4 molto più piccolo di M (100).
# Vediamo come avrei potuto procedere senza fare uno ad uno i tentativi: conto con n
# le prove e le ripeto fino a che riottengo x0:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# riottengo ottengo 4.
# Questo era un brutto generatore. Dà un'idea di come non si possa procedere a caso.
# Proviamo con un'altro.
#
## LungRnd1
# Generatore che era stato proposto in: "Le scienze con il calcolatore tascabile"
# (R.Green, J.Lewis - Muzzio Editore - 1980)
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
# Proviamo direttamente a trovare il periodo:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# ottengo 16384.
# È un valor molto grande (=65536/4). Potrei usare questo generatore per simulare
# qualche semplice fenomento. Dovrò verificare che la distribuzione sia accettabile
# come uniforme. Come abbiamo detto la cosa non è facile. Proviamo, solo, a vederlo
# graficamente, nel modo seguente (prima "normalizziamo" le uscite, ossia le
# trasformiamo in numeri tra 0 ed 1 dividendole per M).
# Idea: genere a caso una x, memorizzarne il valore come u, proseguire generando
# un'altra x e rapresentare il punto u/m ed x/M.
#
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
x <- x0
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
...
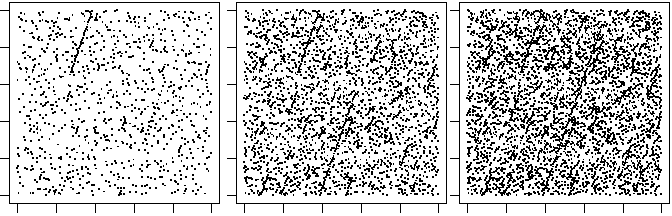 # Hanno un comportamento simile i generatori casuali impiegati nei personal computer
# nella prima metà degli anni '80. Bastano queste uscite grafiche per rendersi
# conto dei limiti di questi generatori.
#
# Per mettere in luce l'opportunità di altri metodi esaminiamo un altro generatore
# che fu molto impiegato.
#
## LungRnd2
# Generatore proposto nel manuale del pocket computer HP-25 (più o meno
# contemporaneo al precedente).
# Genera direttamente numeri tra 0 ed 1 (genera numeri x e ne prende la parte
# frazionaria con x-"parte intera di x")
R0 <- 1/2
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
# Proviamo ad usarlo:
R <- 1/2
R <- Rand(R); R
# 0.4081073
R <- Rand(R); R
# 0.5834226
#
# Proviamo a trovarne il periodo:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
while(alt == 0) if(Rand(R)==R0) {print(n); alt <- 1} else {R <- Rand(R); n <- n+1}
# non si ferma: lo fermo io (con ESC) e stampo n ed R. Ottengo per esempio:
n; R
# 116734 0.5740558
#
# Le uscite sono numeri decimali di parecchie cifre; non abbiamo più
# valori interi come prima, che ciclavano. Questo è un generatore di tipo
# diverso.
# Esaminiamo le ucite graficamente:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
...
# Hanno un comportamento simile i generatori casuali impiegati nei personal computer
# nella prima metà degli anni '80. Bastano queste uscite grafiche per rendersi
# conto dei limiti di questi generatori.
#
# Per mettere in luce l'opportunità di altri metodi esaminiamo un altro generatore
# che fu molto impiegato.
#
## LungRnd2
# Generatore proposto nel manuale del pocket computer HP-25 (più o meno
# contemporaneo al precedente).
# Genera direttamente numeri tra 0 ed 1 (genera numeri x e ne prende la parte
# frazionaria con x-"parte intera di x")
R0 <- 1/2
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
# Proviamo ad usarlo:
R <- 1/2
R <- Rand(R); R
# 0.4081073
R <- Rand(R); R
# 0.5834226
#
# Proviamo a trovarne il periodo:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
while(alt == 0) if(Rand(R)==R0) {print(n); alt <- 1} else {R <- Rand(R); n <- n+1}
# non si ferma: lo fermo io (con ESC) e stampo n ed R. Ottengo per esempio:
n; R
# 116734 0.5740558
#
# Le uscite sono numeri decimali di parecchie cifre; non abbiamo più
# valori interi come prima, che ciclavano. Questo è un generatore di tipo
# diverso.
# Esaminiamo le ucite graficamente:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
...
 ...
# Le uscite sembrano disporsi uniformente. Ma questa è solo un'impressione.
# Proviamo a verifcarlo anche con un istogramma:
R <- 1/2; u <- NULL; for(i in 1:1e4) {u <- c(u,R); R <- Rand(R)}
hist(u,freq=FALSE)
...
# Le uscite sembrano disporsi uniformente. Ma questa è solo un'impressione.
# Proviamo a verifcarlo anche con un istogramma:
R <- 1/2; u <- NULL; for(i in 1:1e4) {u <- c(u,R); R <- Rand(R)}
hist(u,freq=FALSE)
 # L'istogramma sembra confermarci la cosa.
# Questa verifica non è tuttavia sufficiente.
#
# Ad esempio anche per il generatore di numeri casuali visto alla fine della
# volta scorsa, evidentemente "non del tutto casuale" (si ripetono coppie di
# uscite uguali), di cui abbiamo già visto la forma "piatta" dell'istogramma:
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]; hist(x,freq=FALSE)
# L'istogramma sembra confermarci la cosa.
# Questa verifica non è tuttavia sufficiente.
#
# Ad esempio anche per il generatore di numeri casuali visto alla fine della
# volta scorsa, evidentemente "non del tutto casuale" (si ripetono coppie di
# uscite uguali), di cui abbiamo già visto la forma "piatta" dell'istogramma:
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]; hist(x,freq=FALSE)
 # basandosi su queste prove non si hanno indizi della sua "non bontà":
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x1 <- x
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x2 <- x
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
points(x1,x2,pch=".")
# basandosi su queste prove non si hanno indizi della sua "non bontà":
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x1 <- x
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x2 <- x
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
points(x1,x2,pch=".")
 # In questo caso, sapendo come è costruito questo "generatore", possiamo
# costruire una verifica che ne mette in luce i limiti.
# Ecco che cosa si ottiene studiando statisticamente (1) i valori ottenuti
# facendo le differenze tra il valore ottenuto col generatore standard e
# quello ottenuto due uscite prima (mi aspetto una distribuzione triangolare:
# il valore più frequente è 0, e poi via via, andando verso -1 ed 1, le
# frequenze diminuiscono) e (2) quelli ottenuti analogamente con questo
# generatore (uno ogni due valori viene 0: la differenza tra due numeri
# uguali):
n <- 1e4; y <- runif(n)
i <- 1:(n-2); w <- NULL; w[i] <- y[i+2]-y[i]
hist(w,freq=FALSE,seq(-1,1,2/15))
#
x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
i <- 1:(n-2); z <- NULL; z[i] <- x[i+2]-x[i]
hist(z,freq=FALSE,seq(-1,1,2/15))
# In questo caso, sapendo come è costruito questo "generatore", possiamo
# costruire una verifica che ne mette in luce i limiti.
# Ecco che cosa si ottiene studiando statisticamente (1) i valori ottenuti
# facendo le differenze tra il valore ottenuto col generatore standard e
# quello ottenuto due uscite prima (mi aspetto una distribuzione triangolare:
# il valore più frequente è 0, e poi via via, andando verso -1 ed 1, le
# frequenze diminuiscono) e (2) quelli ottenuti analogamente con questo
# generatore (uno ogni due valori viene 0: la differenza tra due numeri
# uguali):
n <- 1e4; y <- runif(n)
i <- 1:(n-2); w <- NULL; w[i] <- y[i+2]-y[i]
hist(w,freq=FALSE,seq(-1,1,2/15))
#
x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
i <- 1:(n-2); z <- NULL; z[i] <- x[i+2]-x[i]
hist(z,freq=FALSE,seq(-1,1,2/15))
 #
# Ci siamo resi conto della complessità dell'argomento. Averlo un po'
# maneggiato ci ha dato un'idea di quanta "matematica" ci sia dietro alla
# messa a punto di uno strumento apparentemente semplice come questo.
#
# Un'ultima osservazione: queste successioni (LungRnd1, LungRnd2) possono
# partire prendendo come valore inziale invece del valore x0 indicato un
# altro valore tra quelli generati. Lo stesso accade per runif.
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa
# partire la successione "casuale" da un dato valore (con lo stesso n ho
# la stessa sequenza)
set.seed(7); runif(3); runif(3)
# 0.9889093 0.3977455 0.1156978
# 0.06974868 0.24374939 0.79201043
set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978; ho riottenuto gli stessi valori:
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo
# in molte situazioni (testare un algoritmo sulla stessa successione di valori,
# controllare simulazioni di fenomeni, memorizzare codifiche segrete, ...).
#
# Accanto a questi "pseudo generatori di numeri casuali" (PRNG) vi sono anche
# degli "hardware random number generator" generati da un processo fisico,
# basati su fenomeni termici, fotoelettrici, quantistici, utilizzati per
# particolari applicazioni, non in ambito statistico.
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
#
# Dopo questa digressione, vediamo alcuni modi in cui si possono realizzare
# rappresentazioni grafiche piane. Abbiamo visto (ad es. qui, qui e qui) come fare il
# grafico di una funzione facendo scegliere automaticamente la scala o scegliendo
# (con xlim e ylim) dove far variare ascisse e ordinate o aggiungendo il grafico
# ad una griglia già scelta. Abbiamo anche visto (ad es. qui) come il parametro
# "col" consente di scegliere il colore con cui realizzare i grafici. I colori
# usabili sono centinaia; i nomi sono elencati dal comando colors(); non mettere
# il colore è come scegliere black. Eccone alcuni: white yellow yellow3 yellow4
# green green4 violet purple pink coral red magenta magenta4 orange brown
# cyan cyan4 blue blue4 grey grey50 black (i colori sono chiamabili anche usando
# le coordinate RossoVerdeBlu: vedi)
#
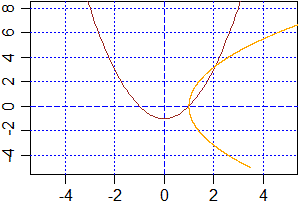
# Ecco come aggiungere (al grafico di g <- function(x) x^2-1) la curva
# y^2/10+1 = x tracciata mediante 2000 segmentini: lines(p,q,...) traccia
# l'insieme dei segmenti con vertici i punti (p,q) dove p e q sono i valori
# descritti in funzione di t, con t che varia tra t1 e t2.
plot(c(-5,5),c(-5,8),type="n",xlab="",ylab="")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=0, h=0, col="blue",lty=2)
g <- function(x) x^2-1; curve(g,col="brown",add=TRUE)
t1 <- -5; t2 <- 8; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2-1,t)
#
# Ci siamo resi conto della complessità dell'argomento. Averlo un po'
# maneggiato ci ha dato un'idea di quanta "matematica" ci sia dietro alla
# messa a punto di uno strumento apparentemente semplice come questo.
#
# Un'ultima osservazione: queste successioni (LungRnd1, LungRnd2) possono
# partire prendendo come valore inziale invece del valore x0 indicato un
# altro valore tra quelli generati. Lo stesso accade per runif.
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa
# partire la successione "casuale" da un dato valore (con lo stesso n ho
# la stessa sequenza)
set.seed(7); runif(3); runif(3)
# 0.9889093 0.3977455 0.1156978
# 0.06974868 0.24374939 0.79201043
set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978; ho riottenuto gli stessi valori:
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo
# in molte situazioni (testare un algoritmo sulla stessa successione di valori,
# controllare simulazioni di fenomeni, memorizzare codifiche segrete, ...).
#
# Accanto a questi "pseudo generatori di numeri casuali" (PRNG) vi sono anche
# degli "hardware random number generator" generati da un processo fisico,
# basati su fenomeni termici, fotoelettrici, quantistici, utilizzati per
# particolari applicazioni, non in ambito statistico.
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
#
# Dopo questa digressione, vediamo alcuni modi in cui si possono realizzare
# rappresentazioni grafiche piane. Abbiamo visto (ad es. qui, qui e qui) come fare il
# grafico di una funzione facendo scegliere automaticamente la scala o scegliendo
# (con xlim e ylim) dove far variare ascisse e ordinate o aggiungendo il grafico
# ad una griglia già scelta. Abbiamo anche visto (ad es. qui) come il parametro
# "col" consente di scegliere il colore con cui realizzare i grafici. I colori
# usabili sono centinaia; i nomi sono elencati dal comando colors(); non mettere
# il colore è come scegliere black. Eccone alcuni: white yellow yellow3 yellow4
# green green4 violet purple pink coral red magenta magenta4 orange brown
# cyan cyan4 blue blue4 grey grey50 black (i colori sono chiamabili anche usando
# le coordinate RossoVerdeBlu: vedi)
#
# Ecco come aggiungere (al grafico di g <- function(x) x^2-1) la curva
# y^2/10+1 = x tracciata mediante 2000 segmentini: lines(p,q,...) traccia
# l'insieme dei segmenti con vertici i punti (p,q) dove p e q sono i valori
# descritti in funzione di t, con t che varia tra t1 e t2.
plot(c(-5,5),c(-5,8),type="n",xlab="",ylab="")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=0, h=0, col="blue",lty=2)
g <- function(x) x^2-1; curve(g,col="brown",add=TRUE)
t1 <- -5; t2 <- 8; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2-1,t)
 #
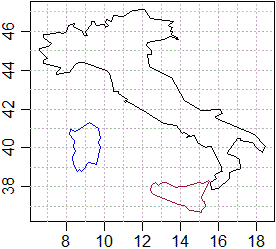
# Ecco come visualizzare delle figure ottenibili congiungendo punti di cui sono
# note le coordinate. Conosco nome e collocazione dei file. Vediamo cosa c'è:
readLines("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",n=3)
# "8,46" "7.87,45.9" "7.6,45.95"
# Sono punti rappresentati mediante coppie di coordinate (dal nome capisco che
# si tratta della penisola italiana), separato da "," e senza commenti iniziali.
# Dunque li carico con:
dati1 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",header=FALSE,sep =",")
# Posso vedere come sono strutturati di dati:
str(dati1)
# 'data.frame': 124 obs. of 2 variables:
# $ V1: num 8 7.87 7.6 7 6.81 6.81 7.2 7.08 6.6 6.6 ...
# $ V2: num 46 45.9 46 45.9 45.8 ...
# carico analogamente altri due file e cerco minima e massima x, minima e massima y:
dati2 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sicilia.txt",header=FALSE,sep =",")
dati3 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sardegna.txt",header=FALSE,sep =",")
mo <- min(dati1$V1,dati2$V1,dati3$V1);Mo <- max(dati1$V1,dati2$V1,dati3$V1)
mv <- min(dati1$V2,dati2$V2,dati3$V2);Mv <- max(dati1$V2,dati2$V2,dati3$V2)
# Scelgo un rettangolo cartesiano che contenga tutti i punti:
plot(c(mo,Mo),c(mv,Mv),type="n",xlab="", ylab="")
abline(h=seq(37,47,1),v=seq(7,18,1),lty=3,col="grey")
lines(dati1,col="black")
lines(dati2,col="brown")
lines(dati3,col="blue")
#
# Ecco come visualizzare delle figure ottenibili congiungendo punti di cui sono
# note le coordinate. Conosco nome e collocazione dei file. Vediamo cosa c'è:
readLines("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",n=3)
# "8,46" "7.87,45.9" "7.6,45.95"
# Sono punti rappresentati mediante coppie di coordinate (dal nome capisco che
# si tratta della penisola italiana), separato da "," e senza commenti iniziali.
# Dunque li carico con:
dati1 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",header=FALSE,sep =",")
# Posso vedere come sono strutturati di dati:
str(dati1)
# 'data.frame': 124 obs. of 2 variables:
# $ V1: num 8 7.87 7.6 7 6.81 6.81 7.2 7.08 6.6 6.6 ...
# $ V2: num 46 45.9 46 45.9 45.8 ...
# carico analogamente altri due file e cerco minima e massima x, minima e massima y:
dati2 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sicilia.txt",header=FALSE,sep =",")
dati3 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sardegna.txt",header=FALSE,sep =",")
mo <- min(dati1$V1,dati2$V1,dati3$V1);Mo <- max(dati1$V1,dati2$V1,dati3$V1)
mv <- min(dati1$V2,dati2$V2,dati3$V2);Mv <- max(dati1$V2,dati2$V2,dati3$V2)
# Scelgo un rettangolo cartesiano che contenga tutti i punti:
plot(c(mo,Mo),c(mv,Mv),type="n",xlab="", ylab="")
abline(h=seq(37,47,1),v=seq(7,18,1),lty=3,col="grey")
lines(dati1,col="black")
lines(dati2,col="brown")
lines(dati3,col="blue")
 # se vuoi evidenziare i punti puoi aggiungere:
points(dati1,col="orange",pch=".", cex=3)
points(dati2,col="orange",pch=".", cex=3)
points(dati3,col="orange",pch=".", cex=3)
# se vuoi evidenziare i punti puoi aggiungere:
points(dati1,col="orange",pch=".", cex=3)
points(dati2,col="orange",pch=".", cex=3)
points(dati3,col="orange",pch=".", cex=3)
 #
# Come detto (vedi) i comandi dati possono essere memorizzati usando il comando
# Save History. I grafici possono essere man mano rieseguiti usando i comandi;
# volendo, ecco come conviene salvare un'immagine. Si clicca su di essa e, dal
# menu che si apre cliccando, la si salva come BitMap e la si incolla su Paint
# (o un altro programma di grafica), si aggiunge quello che si vuole e la si
# ridimensiona. A questo punto o la si copia e salva nel documento in cui si
# sta operando o, da Paint, la si salva in formato GIF, che occupa poco spazio
# e consente di operare successive modifiche, anche dettagliate, con Paint
# (nelle ultime versioni di Windows, conviene, prima di salvarlo, farsi una
# copia del file, quindi memorizzarlo come GIF, attendere un messaggio che
# dice che l'immagine non è salvata perfettamente, quindi incollare l'immagine
# memorizzata e fare Save: l'immagine a questo punto è perfetta; se essa viene
# incollata su una figura già salvata come gif e poi salvata, eventualmente
# cambiando il nome, il salvataggio "perfetto" viene fatto automaticamente).
#
# Vedi QUI per l'uso di locator per evidenziare coordinate di punti o
# tracciare punti (e segmenti) col mouse.
#
# Vedi QUI per aprire/dimensionare nuove finestre (dev.new)
#
# Vedi QUI per aggiungere scritte nei grafici (text)
#
# Vedi QUI per realizzare trasformazioni geometriche
#
# Vedi QUI per realizzare movimenti col mouse
#
# Una funzione per tracciare un poligono regolare di centro C, raggio R, con
# AngIniz che indica la posizione del primo vertice, cob e coi che indicano
# il colore del bordo e il colore interno. Se non voglio colorare internamente
# il poligono basta che come colore dia NULL
pol <- function(C, R, AngIniz, N, cob, coi) {
gr <- function(x) x/180*pi;
ang <- function(i) gr((360/N)*i+AngIniz);
polygon( cos(ang(0:N))*R+C[1], sin(ang(0:N))*R+C[2],border=cob,col=coi) }
plot(c(-5,5),c(-5,5),type="n",xlab="", ylab="", asp=1)
abline(v=axTicks(1), h=axTicks(2), col="orange",lty=3)
pol(c(1,-1),4,70,6,"black","yellow")
pol(c(1,-1),4,70,3,"red",NULL); pol(c(1,-1),4,70+60,3, "blue",NULL)
#
# Come detto (vedi) i comandi dati possono essere memorizzati usando il comando
# Save History. I grafici possono essere man mano rieseguiti usando i comandi;
# volendo, ecco come conviene salvare un'immagine. Si clicca su di essa e, dal
# menu che si apre cliccando, la si salva come BitMap e la si incolla su Paint
# (o un altro programma di grafica), si aggiunge quello che si vuole e la si
# ridimensiona. A questo punto o la si copia e salva nel documento in cui si
# sta operando o, da Paint, la si salva in formato GIF, che occupa poco spazio
# e consente di operare successive modifiche, anche dettagliate, con Paint
# (nelle ultime versioni di Windows, conviene, prima di salvarlo, farsi una
# copia del file, quindi memorizzarlo come GIF, attendere un messaggio che
# dice che l'immagine non è salvata perfettamente, quindi incollare l'immagine
# memorizzata e fare Save: l'immagine a questo punto è perfetta; se essa viene
# incollata su una figura già salvata come gif e poi salvata, eventualmente
# cambiando il nome, il salvataggio "perfetto" viene fatto automaticamente).
#
# Vedi QUI per l'uso di locator per evidenziare coordinate di punti o
# tracciare punti (e segmenti) col mouse.
#
# Vedi QUI per aprire/dimensionare nuove finestre (dev.new)
#
# Vedi QUI per aggiungere scritte nei grafici (text)
#
# Vedi QUI per realizzare trasformazioni geometriche
#
# Vedi QUI per realizzare movimenti col mouse
#
# Una funzione per tracciare un poligono regolare di centro C, raggio R, con
# AngIniz che indica la posizione del primo vertice, cob e coi che indicano
# il colore del bordo e il colore interno. Se non voglio colorare internamente
# il poligono basta che come colore dia NULL
pol <- function(C, R, AngIniz, N, cob, coi) {
gr <- function(x) x/180*pi;
ang <- function(i) gr((360/N)*i+AngIniz);
polygon( cos(ang(0:N))*R+C[1], sin(ang(0:N))*R+C[2],border=cob,col=coi) }
plot(c(-5,5),c(-5,5),type="n",xlab="", ylab="", asp=1)
abline(v=axTicks(1), h=axTicks(2), col="orange",lty=3)
pol(c(1,-1),4,70,6,"black","yellow")
pol(c(1,-1),4,70,3,"red",NULL); pol(c(1,-1),4,70+60,3, "blue",NULL)

 # Hanno un comportamento simile i generatori casuali impiegati nei personal computer
# nella prima metà degli anni '80. Bastano queste uscite grafiche per rendersi
# conto dei limiti di questi generatori.
#
# Per mettere in luce l'opportunità di altri metodi esaminiamo un altro generatore
# che fu molto impiegato.
#
## LungRnd2
# Generatore proposto nel manuale del pocket computer HP-25 (più o meno
# contemporaneo al precedente).
# Genera direttamente numeri tra 0 ed 1 (genera numeri x e ne prende la parte
# frazionaria con x-"parte intera di x")
R0 <- 1/2
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
# Proviamo ad usarlo:
R <- 1/2
R <- Rand(R); R
# 0.4081073
R <- Rand(R); R
# 0.5834226
#
# Proviamo a trovarne il periodo:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
while(alt == 0) if(Rand(R)==R0) {print(n); alt <- 1} else {R <- Rand(R); n <- n+1}
# non si ferma: lo fermo io (con ESC) e stampo n ed R. Ottengo per esempio:
n; R
# 116734 0.5740558
#
# Le uscite sono numeri decimali di parecchie cifre; non abbiamo più
# valori interi come prima, che ciclavano. Questo è un generatore di tipo
# diverso.
# Esaminiamo le ucite graficamente:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
...
# Hanno un comportamento simile i generatori casuali impiegati nei personal computer
# nella prima metà degli anni '80. Bastano queste uscite grafiche per rendersi
# conto dei limiti di questi generatori.
#
# Per mettere in luce l'opportunità di altri metodi esaminiamo un altro generatore
# che fu molto impiegato.
#
## LungRnd2
# Generatore proposto nel manuale del pocket computer HP-25 (più o meno
# contemporaneo al precedente).
# Genera direttamente numeri tra 0 ed 1 (genera numeri x e ne prende la parte
# frazionaria con x-"parte intera di x")
R0 <- 1/2
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
# Proviamo ad usarlo:
R <- 1/2
R <- Rand(R); R
# 0.4081073
R <- Rand(R); R
# 0.5834226
#
# Proviamo a trovarne il periodo:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
while(alt == 0) if(Rand(R)==R0) {print(n); alt <- 1} else {R <- Rand(R); n <- n+1}
# non si ferma: lo fermo io (con ESC) e stampo n ed R. Ottengo per esempio:
n; R
# 116734 0.5740558
#
# Le uscite sono numeri decimali di parecchie cifre; non abbiamo più
# valori interi come prima, che ciclavano. Questo è un generatore di tipo
# diverso.
# Esaminiamo le ucite graficamente:
R0 <- 1/2
alt <- 0; n <- 1; R <- R0
Rand <- function(R) {R <- (R+pi)^5; R-floor(R)}
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
for(i in 1:500) {x <- Rand(x); u <- x; x <- Rand(x); points(u,x,pch=".",cex=2)}
...
 ...
# Le uscite sembrano disporsi uniformente. Ma questa è solo un'impressione.
# Proviamo a verifcarlo anche con un istogramma:
R <- 1/2; u <- NULL; for(i in 1:1e4) {u <- c(u,R); R <- Rand(R)}
hist(u,freq=FALSE)
...
# Le uscite sembrano disporsi uniformente. Ma questa è solo un'impressione.
# Proviamo a verifcarlo anche con un istogramma:
R <- 1/2; u <- NULL; for(i in 1:1e4) {u <- c(u,R); R <- Rand(R)}
hist(u,freq=FALSE)
 # L'istogramma sembra confermarci la cosa.
# Questa verifica non è tuttavia sufficiente.
#
# Ad esempio anche per il generatore di numeri casuali visto alla fine della
# volta scorsa, evidentemente "non del tutto casuale" (si ripetono coppie di
# uscite uguali), di cui abbiamo già visto la forma "piatta" dell'istogramma:
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]; hist(x,freq=FALSE)
# L'istogramma sembra confermarci la cosa.
# Questa verifica non è tuttavia sufficiente.
#
# Ad esempio anche per il generatore di numeri casuali visto alla fine della
# volta scorsa, evidentemente "non del tutto casuale" (si ripetono coppie di
# uscite uguali), di cui abbiamo già visto la forma "piatta" dell'istogramma:
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]; hist(x,freq=FALSE)
 # basandosi su queste prove non si hanno indizi della sua "non bontà":
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x1 <- x
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x2 <- x
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
points(x1,x2,pch=".")
# basandosi su queste prove non si hanno indizi della sua "non bontà":
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x1 <- x
n <- 1e4; x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
x2 <- x
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
points(x1,x2,pch=".")
 # In questo caso, sapendo come è costruito questo "generatore", possiamo
# costruire una verifica che ne mette in luce i limiti.
# Ecco che cosa si ottiene studiando statisticamente (1) i valori ottenuti
# facendo le differenze tra il valore ottenuto col generatore standard e
# quello ottenuto due uscite prima (mi aspetto una distribuzione triangolare:
# il valore più frequente è 0, e poi via via, andando verso -1 ed 1, le
# frequenze diminuiscono) e (2) quelli ottenuti analogamente con questo
# generatore (uno ogni due valori viene 0: la differenza tra due numeri
# uguali):
n <- 1e4; y <- runif(n)
i <- 1:(n-2); w <- NULL; w[i] <- y[i+2]-y[i]
hist(w,freq=FALSE,seq(-1,1,2/15))
#
x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
i <- 1:(n-2); z <- NULL; z[i] <- x[i+2]-x[i]
hist(z,freq=FALSE,seq(-1,1,2/15))
# In questo caso, sapendo come è costruito questo "generatore", possiamo
# costruire una verifica che ne mette in luce i limiti.
# Ecco che cosa si ottiene studiando statisticamente (1) i valori ottenuti
# facendo le differenze tra il valore ottenuto col generatore standard e
# quello ottenuto due uscite prima (mi aspetto una distribuzione triangolare:
# il valore più frequente è 0, e poi via via, andando verso -1 ed 1, le
# frequenze diminuiscono) e (2) quelli ottenuti analogamente con questo
# generatore (uno ogni due valori viene 0: la differenza tra due numeri
# uguali):
n <- 1e4; y <- runif(n)
i <- 1:(n-2); w <- NULL; w[i] <- y[i+2]-y[i]
hist(w,freq=FALSE,seq(-1,1,2/15))
#
x <- runif(n); i <- seq(4,n,4); x[i] <- x[i-2]
i <- 1:(n-2); z <- NULL; z[i] <- x[i+2]-x[i]
hist(z,freq=FALSE,seq(-1,1,2/15))
 #
# Ci siamo resi conto della complessità dell'argomento. Averlo un po'
# maneggiato ci ha dato un'idea di quanta "matematica" ci sia dietro alla
# messa a punto di uno strumento apparentemente semplice come questo.
#
# Un'ultima osservazione: queste successioni (LungRnd1, LungRnd2) possono
# partire prendendo come valore inziale invece del valore x0 indicato un
# altro valore tra quelli generati. Lo stesso accade per runif.
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa
# partire la successione "casuale" da un dato valore (con lo stesso n ho
# la stessa sequenza)
set.seed(7); runif(3); runif(3)
# 0.9889093 0.3977455 0.1156978
# 0.06974868 0.24374939 0.79201043
set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978; ho riottenuto gli stessi valori:
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo
# in molte situazioni (testare un algoritmo sulla stessa successione di valori,
# controllare simulazioni di fenomeni, memorizzare codifiche segrete, ...).
#
# Accanto a questi "pseudo generatori di numeri casuali" (PRNG) vi sono anche
# degli "hardware random number generator" generati da un processo fisico,
# basati su fenomeni termici, fotoelettrici, quantistici, utilizzati per
# particolari applicazioni, non in ambito statistico.
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
#
# Dopo questa digressione, vediamo alcuni modi in cui si possono realizzare
# rappresentazioni grafiche piane. Abbiamo visto (ad es. qui, qui e qui) come fare il
# grafico di una funzione facendo scegliere automaticamente la scala o scegliendo
# (con xlim e ylim) dove far variare ascisse e ordinate o aggiungendo il grafico
# ad una griglia già scelta. Abbiamo anche visto (ad es. qui) come il parametro
# "col" consente di scegliere il colore con cui realizzare i grafici. I colori
# usabili sono centinaia; i nomi sono elencati dal comando colors(); non mettere
# il colore è come scegliere black. Eccone alcuni: white yellow yellow3 yellow4
# green green4 violet purple pink coral red magenta magenta4 orange brown
# cyan cyan4 blue blue4 grey grey50 black (i colori sono chiamabili anche usando
# le coordinate RossoVerdeBlu: vedi)
#
# Ecco come aggiungere (al grafico di g <- function(x) x^2-1) la curva
# y^2/10+1 = x tracciata mediante 2000 segmentini: lines(p,q,...) traccia
# l'insieme dei segmenti con vertici i punti (p,q) dove p e q sono i valori
# descritti in funzione di t, con t che varia tra t1 e t2.
plot(c(-5,5),c(-5,8),type="n",xlab="",ylab="")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=0, h=0, col="blue",lty=2)
g <- function(x) x^2-1; curve(g,col="brown",add=TRUE)
t1 <- -5; t2 <- 8; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2-1,t)
#
# Ci siamo resi conto della complessità dell'argomento. Averlo un po'
# maneggiato ci ha dato un'idea di quanta "matematica" ci sia dietro alla
# messa a punto di uno strumento apparentemente semplice come questo.
#
# Un'ultima osservazione: queste successioni (LungRnd1, LungRnd2) possono
# partire prendendo come valore inziale invece del valore x0 indicato un
# altro valore tra quelli generati. Lo stesso accade per runif.
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa
# partire la successione "casuale" da un dato valore (con lo stesso n ho
# la stessa sequenza)
set.seed(7); runif(3); runif(3)
# 0.9889093 0.3977455 0.1156978
# 0.06974868 0.24374939 0.79201043
set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978; ho riottenuto gli stessi valori:
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo
# in molte situazioni (testare un algoritmo sulla stessa successione di valori,
# controllare simulazioni di fenomeni, memorizzare codifiche segrete, ...).
#
# Accanto a questi "pseudo generatori di numeri casuali" (PRNG) vi sono anche
# degli "hardware random number generator" generati da un processo fisico,
# basati su fenomeni termici, fotoelettrici, quantistici, utilizzati per
# particolari applicazioni, non in ambito statistico.
#
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
#
# Dopo questa digressione, vediamo alcuni modi in cui si possono realizzare
# rappresentazioni grafiche piane. Abbiamo visto (ad es. qui, qui e qui) come fare il
# grafico di una funzione facendo scegliere automaticamente la scala o scegliendo
# (con xlim e ylim) dove far variare ascisse e ordinate o aggiungendo il grafico
# ad una griglia già scelta. Abbiamo anche visto (ad es. qui) come il parametro
# "col" consente di scegliere il colore con cui realizzare i grafici. I colori
# usabili sono centinaia; i nomi sono elencati dal comando colors(); non mettere
# il colore è come scegliere black. Eccone alcuni: white yellow yellow3 yellow4
# green green4 violet purple pink coral red magenta magenta4 orange brown
# cyan cyan4 blue blue4 grey grey50 black (i colori sono chiamabili anche usando
# le coordinate RossoVerdeBlu: vedi)
#
# Ecco come aggiungere (al grafico di g <- function(x) x^2-1) la curva
# y^2/10+1 = x tracciata mediante 2000 segmentini: lines(p,q,...) traccia
# l'insieme dei segmenti con vertici i punti (p,q) dove p e q sono i valori
# descritti in funzione di t, con t che varia tra t1 e t2.
plot(c(-5,5),c(-5,8),type="n",xlab="",ylab="")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=0, h=0, col="blue",lty=2)
g <- function(x) x^2-1; curve(g,col="brown",add=TRUE)
t1 <- -5; t2 <- 8; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2-1,t)
 #
# Ecco come visualizzare delle figure ottenibili congiungendo punti di cui sono
# note le coordinate. Conosco nome e collocazione dei file. Vediamo cosa c'è:
readLines("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",n=3)
# "8,46" "7.87,45.9" "7.6,45.95"
# Sono punti rappresentati mediante coppie di coordinate (dal nome capisco che
# si tratta della penisola italiana), separato da "," e senza commenti iniziali.
# Dunque li carico con:
dati1 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",header=FALSE,sep =",")
# Posso vedere come sono strutturati di dati:
str(dati1)
# 'data.frame': 124 obs. of 2 variables:
# $ V1: num 8 7.87 7.6 7 6.81 6.81 7.2 7.08 6.6 6.6 ...
# $ V2: num 46 45.9 46 45.9 45.8 ...
# carico analogamente altri due file e cerco minima e massima x, minima e massima y:
dati2 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sicilia.txt",header=FALSE,sep =",")
dati3 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sardegna.txt",header=FALSE,sep =",")
mo <- min(dati1$V1,dati2$V1,dati3$V1);Mo <- max(dati1$V1,dati2$V1,dati3$V1)
mv <- min(dati1$V2,dati2$V2,dati3$V2);Mv <- max(dati1$V2,dati2$V2,dati3$V2)
# Scelgo un rettangolo cartesiano che contenga tutti i punti:
plot(c(mo,Mo),c(mv,Mv),type="n",xlab="", ylab="")
abline(h=seq(37,47,1),v=seq(7,18,1),lty=3,col="grey")
lines(dati1,col="black")
lines(dati2,col="brown")
lines(dati3,col="blue")
#
# Ecco come visualizzare delle figure ottenibili congiungendo punti di cui sono
# note le coordinate. Conosco nome e collocazione dei file. Vediamo cosa c'è:
readLines("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",n=3)
# "8,46" "7.87,45.9" "7.6,45.95"
# Sono punti rappresentati mediante coppie di coordinate (dal nome capisco che
# si tratta della penisola italiana), separato da "," e senza commenti iniziali.
# Dunque li carico con:
dati1 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/penisola.txt",header=FALSE,sep =",")
# Posso vedere come sono strutturati di dati:
str(dati1)
# 'data.frame': 124 obs. of 2 variables:
# $ V1: num 8 7.87 7.6 7 6.81 6.81 7.2 7.08 6.6 6.6 ...
# $ V2: num 46 45.9 46 45.9 45.8 ...
# carico analogamente altri due file e cerco minima e massima x, minima e massima y:
dati2 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sicilia.txt",header=FALSE,sep =",")
dati3 <- read.table("http://macosa.dima.unige.it/om/prg/R/rmacosa/sardegna.txt",header=FALSE,sep =",")
mo <- min(dati1$V1,dati2$V1,dati3$V1);Mo <- max(dati1$V1,dati2$V1,dati3$V1)
mv <- min(dati1$V2,dati2$V2,dati3$V2);Mv <- max(dati1$V2,dati2$V2,dati3$V2)
# Scelgo un rettangolo cartesiano che contenga tutti i punti:
plot(c(mo,Mo),c(mv,Mv),type="n",xlab="", ylab="")
abline(h=seq(37,47,1),v=seq(7,18,1),lty=3,col="grey")
lines(dati1,col="black")
lines(dati2,col="brown")
lines(dati3,col="blue")
 # se vuoi evidenziare i punti puoi aggiungere:
points(dati1,col="orange",pch=".", cex=3)
points(dati2,col="orange",pch=".", cex=3)
points(dati3,col="orange",pch=".", cex=3)
# se vuoi evidenziare i punti puoi aggiungere:
points(dati1,col="orange",pch=".", cex=3)
points(dati2,col="orange",pch=".", cex=3)
points(dati3,col="orange",pch=".", cex=3)
 #
# Come detto (vedi) i comandi dati possono essere memorizzati usando il comando
# Save History. I grafici possono essere man mano rieseguiti usando i comandi;
# volendo, ecco come conviene salvare un'immagine. Si clicca su di essa e, dal
# menu che si apre cliccando, la si salva come BitMap e la si incolla su Paint
# (o un altro programma di grafica), si aggiunge quello che si vuole e la si
# ridimensiona. A questo punto o la si copia e salva nel documento in cui si
# sta operando o, da Paint, la si salva in formato GIF, che occupa poco spazio
# e consente di operare successive modifiche, anche dettagliate, con Paint
# (nelle ultime versioni di Windows, conviene, prima di salvarlo, farsi una
# copia del file, quindi memorizzarlo come GIF, attendere un messaggio che
# dice che l'immagine non è salvata perfettamente, quindi incollare l'immagine
# memorizzata e fare Save: l'immagine a questo punto è perfetta; se essa viene
# incollata su una figura già salvata come gif e poi salvata, eventualmente
# cambiando il nome, il salvataggio "perfetto" viene fatto automaticamente).
#
# Vedi QUI per l'uso di locator per evidenziare coordinate di punti o
# tracciare punti (e segmenti) col mouse.
#
# Vedi QUI per aprire/dimensionare nuove finestre (dev.new)
#
# Vedi QUI per aggiungere scritte nei grafici (text)
#
# Vedi QUI per realizzare trasformazioni geometriche
#
# Vedi QUI per realizzare movimenti col mouse
#
# Una funzione per tracciare un poligono regolare di centro C, raggio R, con
# AngIniz che indica la posizione del primo vertice, cob e coi che indicano
# il colore del bordo e il colore interno. Se non voglio colorare internamente
# il poligono basta che come colore dia NULL
pol <- function(C, R, AngIniz, N, cob, coi) {
gr <- function(x) x/180*pi;
ang <- function(i) gr((360/N)*i+AngIniz);
polygon( cos(ang(0:N))*R+C[1], sin(ang(0:N))*R+C[2],border=cob,col=coi) }
plot(c(-5,5),c(-5,5),type="n",xlab="", ylab="", asp=1)
abline(v=axTicks(1), h=axTicks(2), col="orange",lty=3)
pol(c(1,-1),4,70,6,"black","yellow")
pol(c(1,-1),4,70,3,"red",NULL); pol(c(1,-1),4,70+60,3, "blue",NULL)
#
# Come detto (vedi) i comandi dati possono essere memorizzati usando il comando
# Save History. I grafici possono essere man mano rieseguiti usando i comandi;
# volendo, ecco come conviene salvare un'immagine. Si clicca su di essa e, dal
# menu che si apre cliccando, la si salva come BitMap e la si incolla su Paint
# (o un altro programma di grafica), si aggiunge quello che si vuole e la si
# ridimensiona. A questo punto o la si copia e salva nel documento in cui si
# sta operando o, da Paint, la si salva in formato GIF, che occupa poco spazio
# e consente di operare successive modifiche, anche dettagliate, con Paint
# (nelle ultime versioni di Windows, conviene, prima di salvarlo, farsi una
# copia del file, quindi memorizzarlo come GIF, attendere un messaggio che
# dice che l'immagine non è salvata perfettamente, quindi incollare l'immagine
# memorizzata e fare Save: l'immagine a questo punto è perfetta; se essa viene
# incollata su una figura già salvata come gif e poi salvata, eventualmente
# cambiando il nome, il salvataggio "perfetto" viene fatto automaticamente).
#
# Vedi QUI per l'uso di locator per evidenziare coordinate di punti o
# tracciare punti (e segmenti) col mouse.
#
# Vedi QUI per aprire/dimensionare nuove finestre (dev.new)
#
# Vedi QUI per aggiungere scritte nei grafici (text)
#
# Vedi QUI per realizzare trasformazioni geometriche
#
# Vedi QUI per realizzare movimenti col mouse
#
# Una funzione per tracciare un poligono regolare di centro C, raggio R, con
# AngIniz che indica la posizione del primo vertice, cob e coi che indicano
# il colore del bordo e il colore interno. Se non voglio colorare internamente
# il poligono basta che come colore dia NULL
pol <- function(C, R, AngIniz, N, cob, coi) {
gr <- function(x) x/180*pi;
ang <- function(i) gr((360/N)*i+AngIniz);
polygon( cos(ang(0:N))*R+C[1], sin(ang(0:N))*R+C[2],border=cob,col=coi) }
plot(c(-5,5),c(-5,5),type="n",xlab="", ylab="", asp=1)
abline(v=axTicks(1), h=axTicks(2), col="orange",lty=3)
pol(c(1,-1),4,70,6,"black","yellow")
pol(c(1,-1),4,70,3,"red",NULL); pol(c(1,-1),4,70+60,3, "blue",NULL)
