Soffermiamoci sui quesiti proposti 3 lezioni fa. Per mia comodità espositiva, affronteremo le soluzioni con R.
(A) Quale/quali, tra tutti i triangoli di eguale superficie aventi in comune un lato, ha/hanno
perimetro minimo?
# (A) Copia via via da un gruppo di righe
# con solo # al gruppo successivo
#
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
# Ho posizionato e dimensionato opportunamente la finestra
# (comandi non essenziali). Con fg="white" non traccio il
# box; con asp=1 faccio sist. monom.
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
text(8,16.5,"Quando è minimo il perimetro?")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
text(8,15.5,"L'esito non dipende da H")
# Dai grafici si deduce subito che l'esito non dipende da H
# (scalando verticalmente la situazione non cambia in quanto
# le lunghezze di L1 ed L2 variano proporzionlamente).
#
#
# Proviamo a fare qualche congettura (facile, col computer ...):
# Diamo via via il vertice e calcoliamo con il teorema di
# Pitagora L1+L2
# (fai via via dei clic; quando vuoi finire premi ESC)
avvio <- 0; par( mai = c(0,0,0,0) )
while(1==1) {plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey50",lty=2)
lines(c(0,10),c(0,0),col="red")
text(0,-1/2,"0"); text(10,-1/2,"10")
xp <- locator(1)$x; polygon(c(0,10,xp),c(0,0,H),border="blue")
xx <- round((10+sqrt(xp^2+H^2)+sqrt((xp-10)^2+H^2))*1e4)/1e4
if (avvio > 0) text(1,15.5,paste("ex:",yp),adj=0)
yp <- xx; text(1,13.5,xx,adj=0)
avvio <- 1; locator(1) }
# differenza vicino all'asse del lato di base e' piccola (impercettibile
# senza computer); non e' facile convincersi del tutto ...
 #
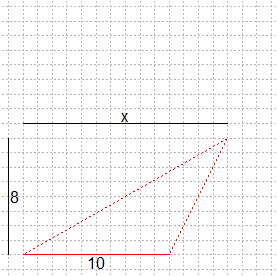
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
#
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
 # E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (facciamolo)
# Potremmo anche derivare il termine con wolframalpha mettendo:
# d ( sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)) ) / dx
#
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
# E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (facciamolo)
# Potremmo anche derivare il termine con wolframalpha mettendo:
# d ( sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)) ) / dx
#
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
 #
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
#
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
(B) Quale/quali, tra tutti i triangoli di eguale perimetro aventi in comune un lato, ha/hanno
superficie massima?
# (B)
# Era già noto ad Euclide che il raggio di luce che arriva in uno
# specchio e quello riflesso formano con lo specchio angoli eguali;
# sappiamo anche (per il Principio di Fermat - vedi) che questo è il
# percorso più breve.
#
# Faccio un disegno per capirci (traccio anche
# l'ellisse con fuochi in (-2,0) e (2,0) )
par( mai = c(0,0,0,0) )
x1 <- -3.5; y1 <- -3; x2 <- 3.5; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="",asp=1)
abline(v=seq(-3,3,1),h=seq(y1,y2,1),lty=3)
abline(v=0,h=0); abline(h=20/12,col="brown")
n <- 80; dx <- (x2-x1)/n; dy <- (y2-y1)/n; I <- 0:n; J <- 0:n
for(i in I) for(j in J) {x <- x1+dx*i;y <- y1+dy*j;
if (abs(sqrt((x-2)^2+y^2)+sqrt((x+2)^2+y^2)-6)<0.05) points(x,y,pch=".",cex=2,col="red")}
polygon(c(-2,0,2),c(0,sqrt(5),0)); polygon(c(-2,2,2),c(0,20/12,0))
text(-2,-1/2,"A"); text(2,-1/2,"B"); text(-0.3,2.7,"H")
lines(c(-2,0,2),c(0,20/12,0),lty=3); text(-0.3,1.5,"K")
text(2.2,2.1,"Q")
 # Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore
# Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore
Commentiamo le soluzioni proposte
 #
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
#
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
 # E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (facciamolo)
# Potremmo anche derivare il termine con wolframalpha mettendo:
# d ( sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)) ) / dx
#
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
# E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (facciamolo)
# Potremmo anche derivare il termine con wolframalpha mettendo:
# d ( sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)) ) / dx
#
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
 #
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
#
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
 # Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore
# Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore