in alcune classi all'inizio della scuola di base
… e, ad es., all'uso della carta quadrettata →
Come differenziare lo sviluppo dei vari temi nei diversi livelli scolastici. Un esempio: il concetto di angolo
1. Premessa
Vogliamo porci il problema di come differenziare, per formalizzazione e sviluppo "tecnico", l'insegnamento dei vari temi nei diversi livelli scolastici. Facciamo emergere, un po' "metaforicamente", i vari aspetti del problema riferendoci allo sviluppo nell'intero arco scolastico di un particolare tema, anzi, dell'insegnamento di uno specifico concetto.
2. La situazione
Ipotizziamo di trovarci ad insegnare matematica in una strana scuola, in cui dovremo seguire gli alunni dalla scuola primaria alla fine della scuola secondaria di 2° grado. Abbiamo già fatto scelte di "impostazione" dell'insegnamento della matematica (traspariranno nel seguito); in questo momento stiamo approfondendo la riflessione su come distribuire nei vari anni lo sviluppo del concetto di angolo.
È una situazione irreale per vari aspetti: possiamo progettare l'insegnamento senza condizionamenti da parte di insegnanti "precedenti" o "posteriori", isolo il ragionamento su un singolo argomento matematico (cosa che in sé sarebbe poco sensata, ma, ripetiamo, è una metafora), …; tuttavia nella sua idealità facilita la messa in luce di alcuni aspetti importanti del problema della differenziazione e del raccordo dell'insegnamento della matematica nei diversi livelli scolastici.
Possiamo, dunque, pensare "liberamente", riferendoci a esperienze precedenti, a nostri studi, …, leggendo cose che ci facciano venire idee (anche cose di "ricerca didattica"), tenendo presente quanto prevedono i programmi scolastici ufficiali, ….
3. Angolo e …
Incominciamo individuando alcuni concetti matematici che, prima o poi, dovremo intrecciare a quello di angolo: direzione, pendenza, misura, rotazione, semiretta, poligono, funzioni circolari, ….
Ci prefiggiamo, nella riflessione sullo sviluppo didattico del concetto, di tener conto degli usi degli angoli (in vari significati) nelle altre discipline, nelle esperienze di vita quotidiana, ….
Teniamo conto dei nostri studi universitari e "personali" di matematica (e di fisica e di filosofia), da cui abbiamo imparato che la geometria è un'area dai contorni non ben definiti, che si sviluppa inizialmente come insieme di tecniche (prima sparse, poi organizzate) di misurazione spaziale diretta e indiretta, poi si intreccia a riflessioni gnoseologiche e metafisiche sulla natura dello spazio e del tempo, … e che la sua autonomia (nelle definizioni e nelle argomentazioni) dalla fisica è una conquista relativamente recente, che passa attraverso le modellizzazioni numeriche dello spazio da parte di Fermat e Cartesio, lo sviluppo graduale del concetto di modello matematico e la messa a fuoco dell'esigenza di dare una fondazione autonoma a una scienza come la matematica divenuta d'uso generale nella società industriale, il delineamento del concetto di sistema formale da parte di Hilbert, ….
Tener conto di questi aspetti ci sarà utile per realizzare itinerari didattici efficaci rispetto alle motivazioni e alle esigenze culturali degli alunni nei vari livelli scolastici, per stabilire se/come/quando introdurre definizioni, dimostrazioni, attività sugli oggetti matematici in quanto tali, ….
4. Scuola primaria (e scuola dell'infanzia)
È il primo approccio alla scuola da parte degli alunni; in esso si gioca in gran parte la possibilità di avviare un rapporto culturale profondo (non solo a fini di valutazione o sopravvivenza scolastica, su binari paralleli o divergenti rispetto alle esperienze extrascolastiche) con l'alunno. Ci preoccupiamo, quindi, di farci una rassegna degli usi del termine e del concetto di angolo (e dei concetti correlati) nella vita quotidiana con i quali può avere a che fare l'alunno (angolo di un oggetto, «dietro l'angolo», «star in un angolo», …, «gira a destra», «vai dritto», punti cardinali, … nelle comunicazioni verbali, nei disegni, nei giochi e nelle varie attività di tutti i giorni).
È una fase in cui il bambino sta arricchendo, con un alto tasso di crescita, il suo bagaglio linguistico-espressivo (relativamente alla lingua naturale, al disegno "non tecnico", …). Anche per questo dovremo stare attenti a non fare precoci specializzazioni matematiche dei significati dei termini; il rischio sarebbe quello di favorire confusioni concettuali, bruciare potenzialità espressive e conoscitive, ….
Terremo conto, poi, che, in questa fase scolastica, per fortuna, non insegniamo solo matematica, ma anche altre discipline: possiamo quindi predisporre itinerari didattici in cui l'aspetto matematico sia naturalmente integrato con gli altri e possa essere fatto emergere gradualmente.
Ci diamo da fare per trovare materiali e resoconti di esperienze didattiche che ci diano spunti e orientamenti per muoversi in queste direzioni (non è facile: quasi tutti i materiali didattici che si possono trovare in una libreria sono esempi in negativo di quello che vorrei fare).
5. Ancora scuola primaria
Come prime attività a cui riferire gli sviluppi matematici dell'area dei concetti legati a quello di angolo (vedi punto 3) pensiamo, ad es., alla descrizione di percorsi seguiti dagli alunni (per compiere "uscite" da scuola, con qualche finalità – ad es. osservare cambiamenti in un orto –, per andare da casa a scuola, …). Questo contesto, in cui si possono integrare e/o fare traduzioni tra descrizioni a parole, descrizioni con disegni, con foto, con prime mappe, …, offre molteplici occasioni per introdurre, precisare, delimitare, … i concetti che ci interessano: le direzioni dei tratti di percorso, le loro pendenze, l'orientamento di edifici, i modi in cui si innestano le strade, i versi delle svolte, la relatività dei riferimenti (rispetto a uno che segue il percorso o rispetto al foglio o …), la misura (che vuol dire tratto più lungo? rispetto al tempo, in linea d'aria, rispetto alla strada da percorrere, … o all'umore con cui lo si è percorso?), le forme e le proporzioni, ….
| Ripensiamo ad alcune attività di disegno svolte in alcune classi all'inizio della scuola di base … e, ad es., all'uso della carta quadrettata → |
 |
Pensiamo anche ad altre attività (inseribili facilmente in vari ambiti di lavoro di ampio respiro): la descrizione dei movimenti di una persona che fa una certa attività, la descrizione di come è fatto e/o di come funziona un certo oggetto, … con vari linguaggi (verbali, iconici, misti, …). Entrano in gioco anche trasformazioni geometriche, forme nuove, …
|
|
|
La delimitazione dei significati diventa importante (per gli alunni) al fine, in queste attività, di riuscire a comunicare capendosi, di essere in grado di passare da una rappresentazione verbale a una grafica, …; la riflessione sui concetti aiuta, poi, a fare meglio le cose; scoprire che a volte ci sono ambiguità, che una stessa parola può essere usata con significati diversi, che in certi ambiti le parole assumono significati più ristretti o diversi da quelli usati nel linguaggio comune, … diventa una tappa verso la organizzazione (in settori, discipline, …) del sapere; ….
Pensiamo di ricorrere ad attività in ambiti esperienziali altrettanto ricchi per introdurre la misura degli angoli, usare gli angoli per modellizzazioni più astratte, …: ad es. il confronto tra indicazione digitale e analogica del tempo, l'uso dell'orologio e della bussola per indicare le direzioni e indicare i versi e le ampiezze (come differenze di direzioni) delle rotazioni, lo studio del fenomeno delle ombre (che è l'altezza del sole? perché e come si deforma l'ombra di un oggetto al passare del tempo o cambiando posizione dell'oggetto? …), ….
|
|
|
6. Quale definizione?
Ci siamo già fatti un po' di idee. Prima di dettagliare meglio gli itinerari ci fermiamo a riflettere su come eventualmente dare la definizione di angolo. Ci è chiara l'importanza di essere graduali nella costruzione dei significati dei vari concetti e nella messa a punto del lessico, oltre che nella "astrazione" delle prestazioni richieste agli alunni (un conto è affrontare direttamente una situazione, un conto è affrontare una situazione problematica reale descritta, un conto è affrontare una situazione problematica già formalizzata o pre-formalizzata, come i cosiddetti "problemi scolastici").
Dobbiamo circoscrivere il concetto di angolo esplicitandone una descrizione formale in termini più astratti? Come?
Come intersezione di semipiani? Ma come si può definire cos'è un semipiano? Come ci potremmo collegare naturalmente alle attività che abbiamo intenzione di svolgere (vedi punto 5)? E questa definizione di angolo quando è stata pensata? in che contesto è significativa? ….
Poi dietro a questo concetto c'è l'idea di angolo come "figura" nel senso di "parte" di piano, con tutti i rischi di pensare (giustamente, pensando agli usi comuni di "figura", di "parte", … e all'uso ambiguo della parola "lato", ora riferito a segmenti, ora a semirette) a un angolo come a una specie di triangolo (se è una figura avrà una certa estensione, finita, è naturale pensare). Dobbiamo sforzarci di pensare al significato che alle parole e alle frasi danno i bambini, cercando di non farci condizionare dalle nostre conoscenze e dai nostri usi, diversi da quelli della lingua comune, che sono il frutto di molti anni di studio.
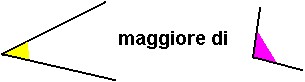
Potremmo definirlo come rotazione (forse l'introduzione del concetto di rotazione è più facile di quella del concetto di semipiano)? Abbiamo letto alcune proposte al riguardo. Ma, rileggendole, ci lasciano perplessi: ci sembra che si confondano ampiezze delle rotazioni, che sono numeri, e angoli, che sono figure.
Ci stiamo infilando in questioni da cui non è facile uscire. Rinunciamo a pretendere di dare una definizione che esaurisca il concetto di angolo. Del resto concordiamo con quanto suggeriscono i programmi: nella scuola di base la geometria va intesa come graduale acquisizione di capacità di orientamento, riconoscimento, localizzazione, organizzazione e schematizzazione nello/dello spazio fisico. Ci limiteremo, dunque, a far lavorare opportunamente gli alunni in contesti che chiariscano, implicitamente, il significato (astratto) del concetto di angolo (della geometria euclidea piana). I contesti più atti a fungere da situazioni prototipo ci sembrano quelli più corrispondenti all'idea di angolo come parte di piano spazzata da una semiretta che ruota: se la semiretta è un raggio di luce, lo sguardo o una traiettoria rettilinea a partire da una posizione fissata, … è possibile evitare che gli alunni si rappresentino mentalmente gli angoli con parti limitate di piano. Le situazioni su cui abbiamo pensato di far lavorare gli alunni (vedi punto 5) sembrano adatte a questo scopo.
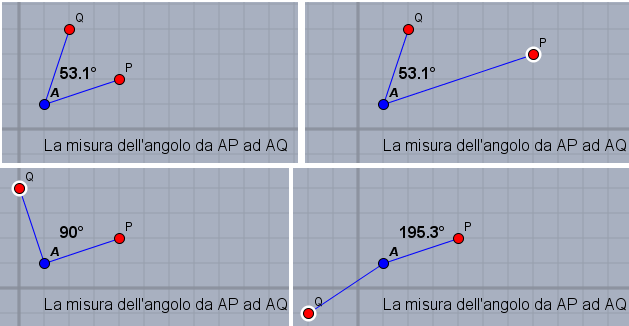
Poi, dopo aver introdotto operativamente questi concetti, potremmo consolidarli anche con delle immagini animate, facilmente realizzabili dall'insegnante, come queste, o con del software di geometria dinamica, usando dei file già pronti, che gli alunni possono usare per attività di esplorazione e sperimentazione, come quelle illustrate dalle seguenti immagini, relative ad un file che consente di ruotare AP o AQ attorno ad A e modificarne le lunghezze (vedi qui):
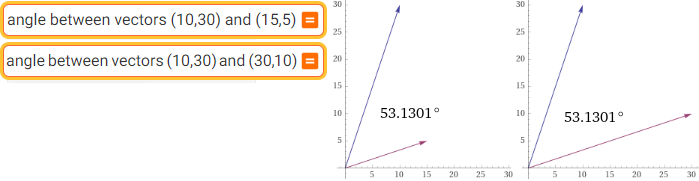
Potremmo utilizzare anche WolframAlpha (vedi):
Un approccio dinamico al concetto di angolo ci consente sia di "congetturare" (vedi la figura sotto a sinistra) che la somma degli angoli di un triangolo è un angolo piatto, sia di "dimostrarlo" (vedi la figura a destra).
 | 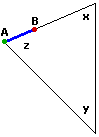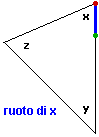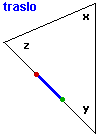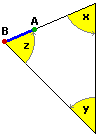 |
7. Scuola secondaria di 1° grado
Nella (strana) scuola "6-18 anni" dove insegniamo, all'inizio della scuola secondaria in genere arrivano alcuni nuovi alunni, che hanno fatto la scuola primaria altrove. Nella progettazione dell'itinerario didattico dobbiamo tener conto anche del problema del raccordo del nostro insegnamento alle loro conoscenze e al loro atteggiamento nei confronti della scuola: come hanno studiato? che cosa sanno? quali attività per esplorare ciò? quali attività per inserirli?
Proporremo inizialmente, a tutta la classe, alcune attività simili a quelle che abbiamo svolto nella scuola primaria. In questo modo cercheremo di affrontare sia una valutazione della produttività del nostro insegnamento sia un'analisi del "livello" di ingresso dei nuovi alunni, senza "prove ad hoc", con cui sarebbe difficile esplorare le loro effettive capacità e si rischierebbe di creare una frattura con gli altri alunni. Cercheremo, comunque, di inserire momenti di lavoro per esplorare specifici aspetti, ad es., stando sempre al concetto di "angolo", eventuali concettualizzazioni degli angoli come figure limitate (potrei pensare ad occasioni in cui, di fronte a due angoli di diversa ampiezza con i lati del più ampio rappresentati con segmenti più corti di quelli dell'altro, come quelli della prima figura del punto 6, si deve individuare qual è l'angolo più ampio).
8. Quale definizione? - bis
Parte dei contenuti dei programmi per la scuola secondaria di 1° grado sono già presenti in quelli della scuola di base. Ovviamente, nel nuovo livello scolastico dovremo avviare a una presentazione più formale e astratta degli stessi. Per l'angolo, sviluppando quanto già osservato nel punto 6, potremmo utilizzare i concetti di semiretta e di rotazione, che, a loro volta, dovremmo in qualche modo introdurre.
Come introdurre la semiretta? Non è certamente praticabile
la strada assiomatica. Non vediamo altro modo che darne una descrizione attraverso l'idealizzazione di una situazione fisica: la
traiettoria (potenzialmente) percorribile a partire da una certa posizione e senza mai cambiare direzione. Potremo dare a questa
descrizione una maggiore formalizzazione e/o farne percepire meglio la natura astratta quando introdurremo (appoggiandosi alle
esperienze di lettura e costruzione di grafici di fenomeni già avviate nella scuola di base) attività di rappresentazione grafica
di funzioni e di rappresentazione analitica di semplici figure:
Non parleremo né di enti primitivi (la cosa avrebbe senso solo nell'ambito di una sistemazione assiomatica, in cui i concetti primitivi sono quelli il cui significato è definito implicitamente dagli assiomi, e non è lasciato all'inutizione, come invece si trova buffamente in molti libri di testo), né tenteremo di dare definizioni più formali di "semiretta" o di "retta". Ci preoccuperemo, invece, nel modo detto, di consolidare negli alunni delle situazioni prototipo più astratte.
Del resto se si prova a comprendere, facendo finta di non conoscerli già, i concetti geometrici (e algebrici) usando solo le definizioni presenti in vari libri scolastici, ci accorgiamo che da esse non si capisce un gran ché: sono in grado di evocare (a chi li conosce già) i concetti ma non di individuarli, essendo piene di aspetti non precisati, di riferimenti ad altri concetti mai definiti, … . Forse la difficoltà maggiore dell'insegnamento è proprio quella di decentrare, di porsi dal punto di vista di che le cose non le sa già, ma deve acquisirle attraverso le attività e i materiali proposti dal docente.
9. Ancora scuola secondaria di 1° grado
Le rotazioni, nelle medie, sono da inquadrare nel contesto di una presentazione più generale delle trasformazioni geometriche. Anche in questo caso è importante tener presente che non si può prescindere dai riferimenti alla fisica: lavorando con trasformazioni geometriche il lessico stesso, i tipi di situazioni analizzate, … sottintendono in genere la presenza della variabile tempo; mentre i passi delle traslazioni sono facilmente descrivibili in termini astratti (riferendosi alle coordinate, senza unità di misura di lunghezza), per la ampiezza delle rotazioni dobbiamo appoggiarci a misure fisiche (col goniometro); …
Ma insegnamo anche scienze. E questa "confusione" con la fisica non è un gran svantaggio: ci consente da una parte di fare delle economie (si possono trattare in un colpo solo argomenti che fanno capo a entrambe le discipline), dall'altra ci consente di chiarire, per contrasto, alcune caratteristiche delle varie discipline. Ad esempio si possono affrontare contestualmente i vettori per rappresentare traslazioni e i vettori per rappresentare spostamenti e si può, poi, mettere a fuoco come i vettori (con la loro addizione) siano utilizzabili come modello non solo per gli spostamenti successivi (confondibili con le traslazioni), ma anche per quelli contemporanei; questo passaggio, culturalmente molto importante, ci consentirà di avviare alcune riflessioni sulla natura dei modelli matematici, sull'uso dei concetti geometrici in altri ambiti, …
Possiamo fare anche altri passi verso la precisazione matematica del concetto di angolo (e dei concetti collegati), in relazione all'avvio delle prime attività di geometria analitica. Si è già accennato a ciò nel punto 8. Un altro aspetto è la quantificazione della pendenza in senso fisico (rapporto tra dislivello e spostamento orizzontale) e il collegamento con la pendenza (coefficiente angolare) delle rette nel piano cartesiano (cambiando la scala orizzontale o quella verticale cambia la pendenza "fisica" della retta y = 2 x, non quella "matematica"). Incominciamo a staccarci dal "goniometro", e ad introdurre il concetto "matematico" di angolo ..., e incominciamo a tracciare grafici e figure col computer ...
| monometrico | 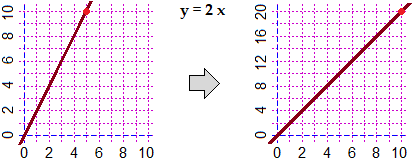 | non monometrico |
10. Scuola secondaria di 2° grado
All'inizio delle superiori si devono affrontare problemi di raccordo analoghi a quelli affrontati all'inizio della scuola secondaria di 1° grado. Ma c'è un ulteriore problema. Sono previsti per la scuola secondaria di 2° grado, senza molte variazioni, gli stessi contenuti geometrici già considerati nei programmi di quella di 1° grado (un'eventuale riflessione su una presentazione assiomatica potrà essere affrontata solo alla fine del triennio, come ha ben messo a fuoco Vinicio Villani, che è stato presidente dell'Unione Matematica Italiana), ma non è chiarito come sia possibile dare una presentazione alternativa: le trasformazioni geometriche sono da affrontare solo in modo intuitivo-sintetico, come nella scuola media? le funzioni circolari devono essere ristrette agli angoli convessi? … Che fare?
Nell'interpretare/tradurre i programmi in itinerari didattici, occorre vedere come proseguire nel passaggio dalla geometria fisica alla geometria matematica. Intanto, come alternativa alla presentazione assiomatica, possiamo riferirci ad una presentazione analitica di alcuni concetti di base (punto, movimento, …) per poi utilizzarli (nello sviluppo della geometria, nella dimostrazioni di alcuni teoremi, …) combinando metodi analitici e sintetici: rispetto alla scuola media il piano cartesiano non sarà più solo un contesto per rappresentare funzioni o per dare forma algebrica a concetti geometrici, ma diventerà il (modello matematico del concetto intuitivo di) "piano"; le variabili e le equazioni diventeranno non solo strumenti per modellizzare relazioni tra grandezze reali ma strumenti per definire nuovi oggetti matematici (figure geometriche); la relazione pitagorica diverrà il cardine per una definizione astratta di distanza; …
Questo cambiamento di prospettiva ci pare una significativa differenziazione rispetto alla secondaria di 1° grado. Per realizzarlo, ossia dare una presentazione matematica ai concetti di movimento, semiretta, angolo, …, dovremo, in qualche modo, dare forma numerica alle direzioni, e non potremo fare a meno di una introduzione (non rigorosa, ma già "matematica") al concetto di lunghezza d'arco (attraverso un passaggio al limite, concetto su cui avrò già lavorato con gli alunni affrontando gli argomenti delle approssimazioni e dei numero reali) e alle funzioni circolari in senso pieno (seno e coseno come componenti del versore, tangente come relazione tra inclinazione e pendenza). Ciò per altro (volendo essere dei "buoni insegnanti") è inevitabile, dal momento che ora, da qualche anno, sono previste prime attività di area "fisica".
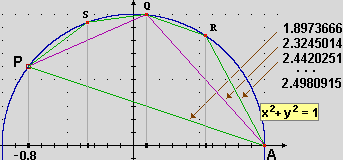 |
| Il calcolo della lunghezza dell'arco AP |
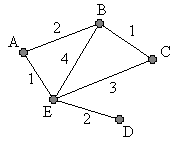
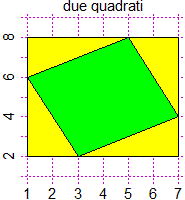
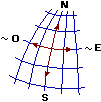
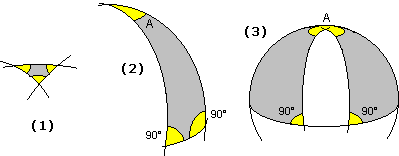
Affinché poi, alla fine del triennio, diventi possibile una riflessione sull'approccio assiomatico (ma non solo per questo), sin da ora cercheremo, rispetto alla scuola media, di avviare ad altre astrazioni. Ad esempio potremo mettere in luce che, in matematica, si possono usare anche spazi più "poveri", in cui non si parla di angoli, in cui i punti sono in quantità finita, … (i grafi per rappresentare reti ferroviarie [vedi], reti stradali, …); che un quadrato rappresentato in un sistema non monometrico potrà apparire con angoli diversi per il goniometro; che si possono definire distanze diverse (con la distanza urbanistica il cerchio di centro (0,0) e raggio 1 appare graficamente come un quadrato); che il concetto di eguaglianza è relativo (dire che due triangoli, o due altre figure, cioè due insiemi di punti, sono uguali come figure non vuol dire che sono uguali come insiemi, se no sarebbero lo stesso oggetto, ma che uno può essere trasformato nell'altro con un movimento o con una isometria o con una similitudine o … a seconda delle considerazioni "geometriche" che voglio fare); che su una superficie terrestre "sferica" un polo e due punti sull'equatore con longitudine differente di 90° possono essere congiunti con tre percorsi rettilinei formando un triangolo con angoli di somma 270°; …
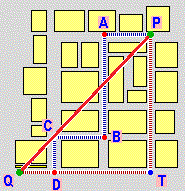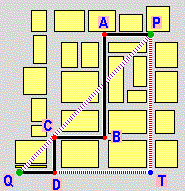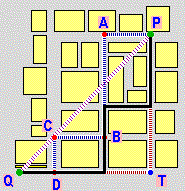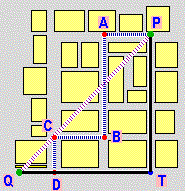 |
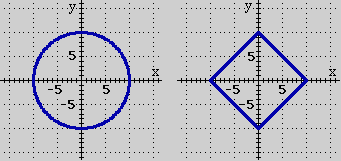 |
| √(x²+y²) |x|+|y| | √(x²+y²) = 10 |x|+|y| = 10 |
 |  |
| ||
In questo passaggio dalla geometria intuitiva alla geometria formalizzata, accanto all'esigenza di precisare in modo non ambiguo cosa sono le definizioni, viene focalizzata quella di precisare quando una argomentazione sia verificabile senza ombra di dubbio. In altre parole occorre chiarire ruolo e significato delle dimostrazioni. Dopo averlo fatto in contesti più semplici, come quelli dell'artimetica e della risoluzione delle equazioni più elementari (che sono quelli che vengono affrontati nei corsi di logica matematica), i cui è più facile mettetere a fuoco e verificare in modo oggettivo i vari passaggi con cui di può dedurre una proprietà a partire da altre assunte come vere o già dimostrate, nel caso della geometria occorre evidenziare la difficoltà nello svolgere argomentazioni separando le "intuizioni suggerite" da una figura (di cui sono pieni i libri di testo più diffusi) dai "ragionamenti controllabili". Dobbiamo aver chiaro che l'obiettivo non è dimostrare tutto quello che si fa, ma è quello di mettere a fuoco il ruolo delle (definizioni e delle) dimostrazioni.
11. Concludendo
Non proseguiamo questa "simulazione" fantastica. Facciamo solo qualche cenno, attraverso alcune immagini, ad altri contesti "matematici" (ma non solo "matematici") in cui, nel percorso didattico, entra in gioco in modo decisivo il concetto di angolo:
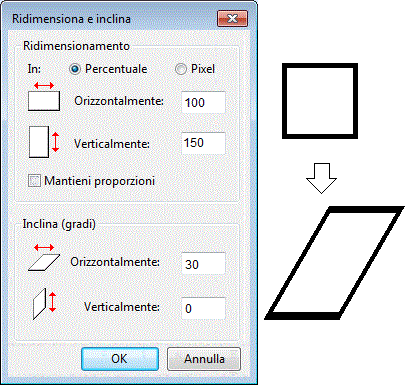 |
    |
|
|
|
|
Pur avendo toccato solo alcuni aspetti, speriamo di aver sottolineato come,
affrontando, anche concretamente, in una specifica attività didattica, i rapporti con un altro livello scolastico, sia importante
tener conto di quanto e come devono essere delineati e precisati natura e ruolo della matematica rispetto alle altre discipline e ai
sistemi di conoscenze degli alunni. Quanto qui discusso per il concetto di "angolo" può fornire spunti per affrontare altri temi.