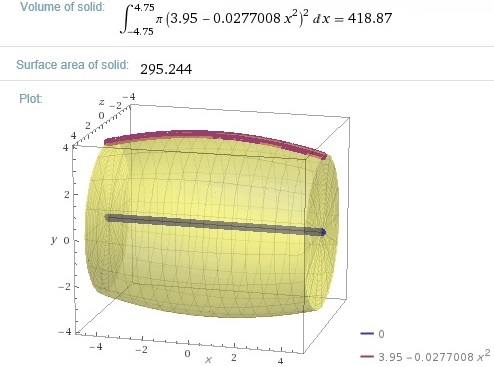
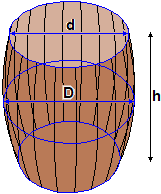
Se D e d sono il diametro massimo e il diametro minimo (interni) ed h è l'altezza (interna), la capacità della botte è, approssimativamente,

π·h·(3·d² + 4·d·D + 8·D²) / 60

Questo è il volume esatto se le doghe hanno curvatura perfettamente parabolica. Se D = d si ritrova la formua per il volume del cilindro. Il volume può essere ottenuto col "metodo dei dischi" (vedi): • cerco la parabola y=a*x^2+c nel piano x,y che va da x=-h/2,y=-d/2 a x=h/2,y=d/2 che passa per x=0,y=D/2. x=0, y=D/2 → c=D/2;  x=h/2, y=d/2 → a*(h/2)^2+D/2 = d/2 → a=(d/2-D/2)/(h/2)^2 la parabola:  y = (d/2-D/2)/(h/2)^2*x^2 + D/2 • posto f(x) = (d/2-D/2)/(h/2)^2*x^2+D/2 devo calcolare l'integrale tra -h/2 e h/2 di π·f(x)²; per farlo facilmente uso WolframAlpha. Scrivo:   integrate pi*((d/2-D/2)/(h/2)^2*x^2+D/2)^2 from -h/2 to h/2 e ottengo:

Considero il caso di una botte con le misure "interne" D = 7.9 dm, d = 6.65 dm, h = 9.5 dm.  Uso i "dm" in modo che il risultato in "dm³" sia esprimibile anche in "litri". La sezione raffigurata sopra e la visione tridimensionale a lato sono riferite a questo caso. Calcolo il volume usando R: V = function(h,D,d) pi*h*(3*d^2 + 4*d*D + 8*D^2)/60 V(9.5, 7.9, 6.65) # 418.8702 (litri) Posso anche calcolare l'integrale usando R source("http://macosa.dima.unige.it/r.R") D = 7.9; d = 6.65; h = 9.5 f = function(x) (d/2-D/2)/(h/2)^2*x^2+D/2 g = function(x) f(x)^2*pi; integral(g, -h/2,h/2) # 418.8702 Ecco, sotto, come posso ottenere con R la figura qui a destra:   BF=4; HF=4; BOXW(0,0,0,0) # I use BOXW to reduce white space x = c(-7.9/2,7.9/2); y = c(-7.9/2,7.9/2) ; w = c(0,9.5) # the box z = array(c(w[1],w[1],w[1],w[1]), dim=c(2,2)) th = 120; ph = 40 F = persp(x,y,z, theta=th,phi=ph, scale=FALSE, xlim=x,ylim=y,zlim=w,           d=3,border="brown") # Metto  border="white",box=FALSE  e poi  co="white"  se non voglio il box

co="red"
axes = function(F) { 
  lines(trans3d(c(0,0),c(0,0),c(0,w[2]),pmat=F),col=co)
  lines(trans3d(c(0,x[2]),c(0,0),c(0,0),pmat=F),col=co)
  lines(trans3d(c(0,0),c(0,y[2]),c(0,0),pmat=F),col=co)
  lines(trans3d(c(0,0),c(0,0),c(w[1],0),pmat=F),col=co,lty=3)
  lines(trans3d(c(x[1],0),c(0,0),c(0,0),pmat=F),col=co,lty=3)
  lines(trans3d(c(0,0),c(y[1],0),c(0,0),pmat=F),col=co,lty=3) }
axes(F)
t=seq(0,9.5,0.1)
lines(trans3d(0,f(t-9.5/2),t,pmat=F),col="black")
for(a in seq(0,360,360/20)) lines(trans3d(cos(a*pi/180)*f(t-9.5/2),sin(a*pi/180)*f(t-9.5/2),t,pmat=F),col="black")
a = (0:50)*2*pi/50
lines(trans3d(cos(a)*d/2,sin(a)*d/2,0,pmat=F),col="blue")
lines(trans3d(cos(a)*d/2,sin(a)*d/2,9.5,pmat=F),col="blue")
lines(trans3d(cos(a)*D/2,sin(a)*D/2,9.5/2,pmat=F),col="blue")