
A: ellisse B: parabola C: iperbole
[se ho l'occhio nel vertice del cono tutte le curve disegnate, essendo sulla superficie del cono, mi appaiono circolari]
 |
Coniche descritte come {P | d(P, O) = e·d(P, r) } [insieme dei punti le cui distanze da un punto fissato e una retta fissata si mantengono tra loro proporzionali] O e r sono fuoco e direttrice A: e = 2, iperbole (e > 1) B: e = 1, parabola (distanze da O e da r si mantengono uguali) C, D: e = 0.75, 0.5, ellissi (e < 1) per e → 0 curva → cerchio Iperboli ed ellissi hanno un centro di simmetria; hanno quindi due fuochi (e due direttrici) tra loro simmetrici. [nella figura a sinistra come fuoco si è presa l'origine degli assi e come direttrice la retta x=1; nel caso, ad es., della parabola tracciata la condizione sotto un'altra raffigurazione di coniche, espresse in coordinate polari, con e=2, e=1, e=0.5] |

e: eccentricità
| Ellisse descritta come {P | d(P, A) + d(P, B) = k} con k>0 A e B sono i fuochi |  |
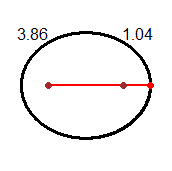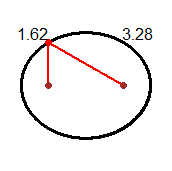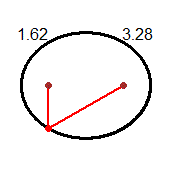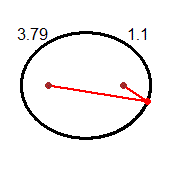
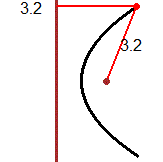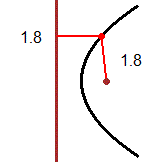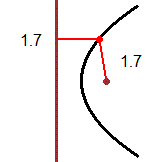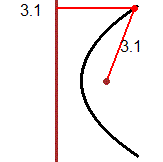
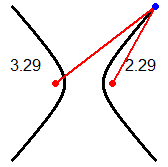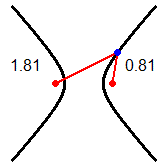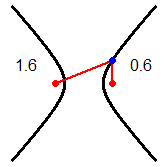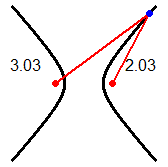
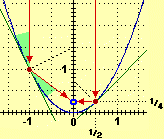  | Un raggio di luce orizzontale che parta da un fuoco di uno specchio a forma di cilindro ellittico verticale arriva nell'altro fuoco; due persone collocate nei fuochi di una stanza ellittica si possono ascoltare l'una con l'altra meglio che se, a parità di distanza, fossero collocate in altre posizioni. Un raggio di luce che colpisca uno specchio parabolico arrivando parallelo al suo asse viene riflesso in modo da passare per il fuoco dello specchio; su un principio simile si basano i fari e le antenne paraboliche. Fenomeni di riflessione di questo tipo sono all'origine dell'uso della parola fuoco per indicare i punti caratteristici delle coniche descritti sopra. |