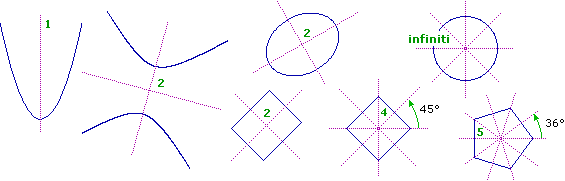
Esempi di figure piane simmetriche, cioè dotate di assi di simmetria: rette che le tagliano in due parti tra loro speculari, ovvero rette rispetto alle quali possono essere "ribaltate" senza cambiare aspetto; alcune con 1 solo asse di simmetria, altre con 2 o più assi di simmetria:
	Le figure piane dotate di almeno due assi di simmetria hanno anche un centro di simmetria, il punto di intersezione tra i due assi. Nella figura a destra dal punto A si passa ad A' con una simmetria rispetto all'"asse" s, da A' si passa ad A" con una simmetria rispetto all'"asse" r; A e A" risultano essere simmetrici rispetto al "centro" C, ossia C è il punto medio del segmento A e A". Ma avere un centro di simmetria, come nel caso della figura a sinistra, non implica avere un asse di simmetria.
Nello spazio tridimensionale si considerano figure simmetriche quelle dotate di piani di simmetria: piani che le tagliano in due parti speculari (un uomo sull'attenti è grosso modo simmetrico rispetto al piano che passa per naso e colonna vertebrale). Così come un cerchio è simmetrico rispetto a qualunque retta che passa per il suo centro, così una sfera è simmetrica rispetto a un qualunque piano che passa per il suo centro. Figure dotate di almeno due piani di simmetria hanno anche un asse di simmetria: è l'intersezione dei due piani di simmetria (si pensi a una bottiglia di vino "schiacciata", come quella raffigurata a lato). Figure dotate di due assi di simmetria hanno anche un centro di simmetria: è il punto di intersezione tra i due assi (si pensi a un pallone da rugby).