model and
reality
On some mathematical concepts / themes to be faced in the first years of school
("interwoven" within teaching units)
[primary - A primary - B lower secondary upper secondary - A upper secondary - B school]
The concept of model
The same contents present in the document relating to the next school level are more or less faced, with a different slant.
The indications refer to how much should be dealt with in kindergarten and in the first part of primary school.
Mathematics can be called the science of models. The concept of model must therefore play a central role in its teaching from the first levels.
The theme of modeling unites all forms of knowledge; this offers numerous and fruitful opportunities for interactions between the teaching of mathematics and that of the other disciplines.
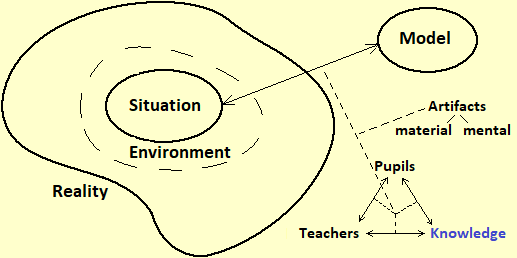
The following figure illustrates the relationship between "model" and "reality". Given a real situation, a model is a simplified representation that illustrates some aspects, for certain purposes. Depending on the purpose there may be different models of the same situation (an airplane model may have the same shape and color as a real airplane but not fly, or it may not resemble a real airplane but fly). The "goodness" of a model depends on its adequacy to the objectives for which it was built (to better highlight some aspects, to generalize some properties, to facilitate comparison with other situations modeled in a similar way, ...). The preliminary phase of the modeling circumscribes the aspects of reality involved in the problem to be studied. In the following diagram, the environment is the part of reality that is isolated, not in detail, in this way, and the situation is the complex of aspects of the phenomenon to be modeled (including assumptions, intuitions, perceptions, intentions, ... of who builds the model) which will be taken into account in the representation:
| model and reality |
 |
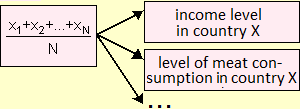
The same model can be used to represent different situations. A very simple example is the concept of addition, which can be used to indicate the total value of two amounts of money, the temperature reached by the thermometer starting from a certain value after a certain increase, the day of the month that from today will be reached in a certain number of days, … Another common example is the concept of arithmetic mean, which can be used to indicate, in a given country, per capita consumption of meat, the average family income, the average height of the twenties, …
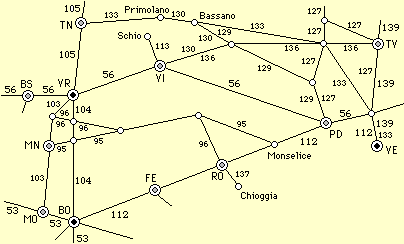
And the same situation,depending on the needs, can be represented with different models. The figure below on the right reproduces part of the graphic index printed on the first pages of a railway timetable: it is a map in which the railway lines are reproduced and the relevant time frames are shown; it is a different model from a usual map in that it does not correctly represent distances and directions.
 |  |
In many cases it is necessary to reinterpret the model by verifying its adequacy to represent the studied phenomenon and possibly to clarify the situation to be modeled. In the diagram we put a double arrow
The figure examines not only the model-reality relationships but also the "tools" used to build the models and how their development interacts with the educational process, i.e. with pupils, teachers and the whole of knowledge (disciplines, disciplines, techniques, .…).
Models are abstract representations of "real" objects or phenomena (of a material type: a topographic representation is the model of a territory; of a social type: the concepts of "verb", "noun", ... are models for representing certain elements of verbal communication; ... or abstract type: the "commutative property" is a model to describe an aspect of some mathematical operations).
Models are built using cognitive artifacts, i.e. "material objects" (paper, signs, sounds, colors, ...) or ad hoc "artificial constructions" (language, concepts, ...) that man uses as a prosthesis of his mind. The term "cognitive artifact" was introduced by Donald Norman in 1993 (Norman D.A., Things that Make us Smart, Wesley Publishing Company, Addison, 1993), , while that of "prosthesis tools" was proposed by Jerome Bruner in 1986 (Bruner J.S., Actual Minds, Possible Worlds, Cambridge, Mass., Harvard University Press, 1986).
The development of cognitive artifacts to model situations does not happen episodicly, but in a social context of cultural growth that is gradually being organized into structured forms of knowledge, which are transmitted from one generation to another through educational processes, in which pupils and teachers interact with each other and with knowledge, the one under construction and the consolidated one. These reciprocal interactions are described by the triangle shown at the bottom right in the initial figure.
What has been observed so far applies to all disciplines and organized forms of knowledge. But mathematics has the specificity of not being characterized by a particular area of problems or phenomena that seeks to model (such as physics, history, linguistics, ...), but by the type of artifacts it employs for the construction of models, and which are used in all other disciplines. So the graphic diagram seen above (which in itself is a simplification) in order to represent the situation of the teaching of mathematics must at least be enriched with the vertical hatch depicted on the side: the artifacts, for mathematics, soon, from cognitive tools become objects of knowledge, from models that "abstract" from situations become gradually "concrete" tools to develop new abstractions, in a never-ending spiral. Mathematical knowledge, which arises from modeled contexts, is organized internally not on the basis of these, but on the relationships and structural analogies between its artifacts. | 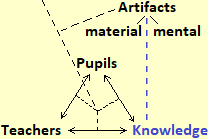 |
The situation, then, becomes more complex as both the "triangle", and the type of "artifacts", with the advent of computer science, have become more articulate: the software has become an "animated" interlocutor that interacts between the different subjects, in ways depending on the use that is made of it and the awareness with which it is used. Without further complicating the previous schematization, it should be borne in mind that the software now has, and will increasingly have, a decisive impact in the way different aspects interact with each other.
In summary, however, we can say that the study of mathematics is articulated in the (non-linear) relationship between posing problems, modeling situations to deal with the solution of problems, building and resorting to theories that internally organize the relationships between the artifacts used for the construction of models and develop new artifacts.
All this makes the role of the teacher crucial in mathematics education. He must:
• design and curate educational pathways that give concreteness to artifacts as they go further away from elementary forms of perception,
• to bring out "reality"-"abstract concept" conflicts (from those between "physical" and "mathematical" mirrors to those between "common" language and "mathematical" language, for example when talking about angles and sides or about rectangles, rhombuses, …, and to the many other conflicts present since the first teaching experiences)
They are conflicts that, if not explicit, risk being sources of misconceptions, while, if faced, they are an opportunity to transform a "destructive opposition" into a "productive dialectic", which contributes to building an adequate image of mathematics as discipline.
• educate to the choice of models (there is no "best" model) depending on the needs and "resources" (physical and conceptual artifacts) available,
• organize teaching so that references to real objects or situations are not only pretexts but also establish virtuous relationships with the extra-curricular knowledge (and motivations) of the pupils, decentralizing, trying to have as a reference not only their own knowledge and motivations but, in a dialectical relationship, also those of the pupils,
• and give organicity to the knowledge they have acquired in the mathematical field (even integrating the study of problematic situations with the development - starting from them - of new concepts and the consolidation of some operational skills through appropriate exercises, which depend on the level of knowledge and technologies historically available) so that they become a solid starting ground for new abstractions,
• all this taking into account that, especially in the first levels of education, the building of virtuous relationships with the extra-school also depends on the involvement of "families": it is necessary to make them participate "culturally" in the educational project that is being carried out (participating "culturally" does not mean "to make the repeaters", but to collaborate with teachers in the construction of relationships between school activities and extracurricular life); this is one of the most difficult tasks; this aspect should also be properly included in the "educational triangle" considered above ...
HERE you will find some examples that illustrate the "the limits of the models". This is an aspect, also mentioned earlier (when we have observed that the same situation can be represented with different models) and that is also taken up in later places, to which it is very important to emphasize in teaching.
Descriptive statistics (and calculus of probabilities)
| Descriptive statistics lend itself to the introduction in significant contexts of many basic mathematical concepts, from numbers to approximations, from the concept of function to graphical representations of numerical relationships. This, at least, if the statistics − which more than 20 thousand years ago constituted the first mathematization activity of man (the use of marks cut into bones and other artifacts to compare quantity of days, objects, people, ...) and can be addressed even in nursery school − is not reduced to being an additional theme to be taught separately from the other themes. The descriptive statistics tools then serve as points of reference for the subsequent introduction to probability. HERE are links to programs that can be used for statistical processing, which the teacher can use. |  |
The previous figure referred to a typical activity that can be faced in preschool (in the last year of preschool - age of 4 or 5 years - the weather conditions can be recorded on a board and then the relative histogram can be built month by month), and which can also be addressed at the beginning of elementary school - age of 5 or 6 years - adding other information in addition to meteorological information (absences, written notes on significant facts, ...). The following figures refer to similar activities, in which the graphic representation intertwines, operationally, with the first uses of numbers (the columns of the histograms are flanked by numbers that allow to express their heights): on the left, the children who mark the places of their holidays (sea, hill, mountain, lake, cities) and then represent this information on squared paper; on the right they similarly mark what is their favorite pastime and then count how many are those who have chosen the ball and the bicycle.
 |  |
The figure alongside represents the ways in which pupils of a class (all, and boys and girls) arrive at school. The examples we are seeing highlight another aspect: statistics must inevitably refer to non-mathematical contexts, and therefore, especially in the first years of school, it offers significant and natural opportunities for interactions between different subject areas, and between different areas of mathematics itself, which only in the following years can be focused and become the subject of in-depth study and technical consolidation. Statistics also allow you to start focusing well (even with simple examples like these) which, depending on what interests you, for the same phenomenon, you can consider different mathematical models that highlight or neglect different aspects. |
 |
 |
In the first years of school, passing to the case in which "forecasts" are made, on the basis of statistical considerations, beliefs or information of various kinds, it is already possible to make probabilistic evaluations.
Complex problems must not be faced, but the concept of "probable", which is present in communications and verbal messages with which children have dealt from the earliest years, must be focused, referring to simple situations of life. • With the "wheel of fortune" reproduced on the side, depending on the part on which the arrow stops (the yellow one, the cyan one or the red one), you have three prizes of different value. What is the part on which the arrow is most likely to stop? (that is, what is the largest "slice"?) And the one on which it is least likely to stop? • Is it more likely to snow in September or January? Why? • The Milan-Inter match is about to take place. For you, which team is most likely to win? |
They are simple examples, but which are also useful as a "vaccine" against the pseudo-definitions of probability as a ratio "favorable
Number and arithmetic operations
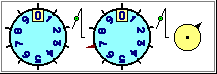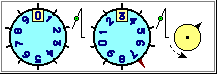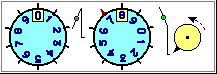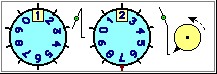
We have already considered the first examples of the use of numbers in the statistical field. It regards situations where they are employed to count. In the child's experiences, however, there are many other uses of numbers, recalled by the following images: numbers used to identify positions (the plates of the gates along the road and those of the apartments inside a block of flats, the floors that can be reached by lift, ..., in which letters also intervene to add other "numbers", in which the numbers can be all even or all odd, in which the number 0 and the negative numbers are also used, ...), numbers that represent orders of arrival at a counter (and which arrived at 99 start from 00), telephone numbers ( that children have to memorize, saying them differently from how they read numbers to count), the number plates of cars (in which not only digits appear), bus numbers (numbers to indicate lines, numbers to indicate days, numbers to indicate times, in hours and minutes), the numbers of the TV channels (with the remote control I can make increases and decreases per unit, and I can easily learn to write multi-digit numbers), …

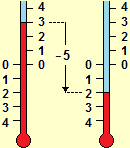
The use of 0 as an indicator of a reference position (and the use of negative numbers), as well as in the case of lifts, is present in other situations, such as in environmental thermometers (see figure below on the right) and in the thermometers of refrigerators. Below left an animation that can consolidate, operatively, the understanding of positional writing. The numbers for counting, identifying positions, measuring temperatures, … inevitably also refer to the operations (increases and decreases) that give a structure to the numbers.
 |
 |
The following images illustrate a further (conceptual and practical) aspect of numerical mastery that must be started in the first years of school: the use of numbers to represent and operate with monetary values, their representation through the abacus, linking with the use of histograms.
| 1 euro divided into 4 equal parts |
 |  |
In everyone's life, even of less educated people, there is a strong link between the experience with money and the formation of the "abstract" concept of number: to understand the functional use of money as a tool to exchange objects between them completely different it is necessary to abstract from the representation of concrete quantities. In the use of money, cardinal, ordinal, measurement, algorithmic, positional writing aspects, … come into play. Reflecting on this, and on the other aspects highlighted in the previous paragraphs, it is evident that the didactic proposals that reduce numerical learning to the separate development of ordinal and cardinal skills are completely absurd.
In the initial years of school, it is necessary to consolidate the understanding of (and the interaction between) different meanings of numbers, in all pupils, socializing their different experiences, and inviting parents (after having involved them in the educational project) to let them experiment the different contexts of use. Some images that recall other typical activities that can be tackled (operationally, without premature and misleading formalizations, which can negatively affect the processes of building knowledge, and know-how, which children, individually and through peer interactions, are activating):
| the temperatures recorded at a fixed time |  |
|
the strips that reproduce the height of the seedlings in the wheat field (or of the bean plant or …) or, when they are too long, on a "small scale" (1 square = 2 cm or ...) |  |
| how many minutes have passed? |
 |


For deepenings, we refer to the document relating to the subsequent years of primary school. We limit ourselves to some information.
It makes no sense (neither "didactic" nor "cultural") to tackle calculation in general by referring to generic numbering bases.
Another thing is to start (operationally, with "changes" of measurement units) to the use of numerical notations used in time measurement (bases 12, 24, 60), on which pupils already have operational skills acquired gradually during the course of the their life.
We have said, and exemplified, that the formation of the ability to operate with numbers must be based on concrete models and closely linked to problematic situations, for a less superficial and more lasting acquisition. We observe that with concrete models we do not mean at all the so-called "structured materials" (diffused by publishing houses that have profit as their "sole" objective), which are a typical example of abstract models. Numerical competence and operational mastery of arithmetic properties must be consolidated in the "contexts"; thanks to the presence of these conceptual "prototypes", it will then be possible to transfer them to activities with pure numbers..
Already in the first years of primary school, pupils must begin to gradually acquire the ability to switch "spontaneously" from one form of representation to another of the most commonly used ways of representing ratios, in particular by referring, in addition to the measurement of time, to the sizes of commonly used beverage containers. These aspects will then be an occasion for further study in the following years of primary school.

|
It is also possible, if desired, to start a first use of pocket calculators. We remind that their use is important if pupils with dyscalculic difficulties are present (for this problem, we refer to the considerations made HERE, in the section dedicated to the lower secondary school). The main objective should be to explore (at a first level) some knowledge about numbers and functions (how the numbers introduced when the function keys |  |
It may be useful, especially in these early school years, to use animated images, such as THESE, which summarize the procedures performed.
Diagrams, formulas and functions
The use of the various graphic representations greatly facilitates the reasoning. It is also the way in which mathematical elaborations (relating to sociological investigations, economic situations, technical-scientific phenomena, …) are generally communicated to us by the mass media. It is therefore essential that teaching educates from the earliest years to their use. In the previous paragraph we have already seen many examples in this regard. The following figures give an idea of other activities to which, in the first years of primary school, the use of graphic representations can be intertwined: the first image is the reproduction of a diagram made by pupils of a class to record and represent (weekly) the duration of the day, the second contains the graphs of the growth of different plants in different environmental conditions, the third is the graph of the body temperature of a sick person.
| |
| hours of light and dark recorded weekly from December to July |
 | 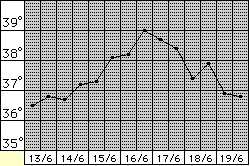 |
The last two figures represent quantities that vary as a function of time: these types of 1 input and 1 output function, in which the independent variable (the input) is time, are the easiest to introduce and those that give more clearly the idea of the meaning of the charts. Below a simpler example, which in the first class should precede the body temperature graph.

The concept of function is intertwined with all areas of mathematics. In addition to these functions (in which the output is not generated by a calculation procedure) all the operations that we focused on in the previous paragraph are also functions. The block diagrams (histograms with crosses), which we discussed in the paragraph on statistics, are also functions: to each type of holiday resort is associated the number of pupils (represented by a column of crosses) that passed them in that way, each mode of getting to school is associated with the number of pupils arriving there with that way, …
Graphs are another powerful tool, both from a linguistic and mathematical point of view, of which pupils easily understand use and role: from the first examples to describe the "path" and "transformations" of some goods (under a graph which describes, in a first approximation, where the ice cream produced by the ice cream shop comes from) or to decompose a monetary value, to the analysis of the cost items of a good (the formation of the price of a bottle of wine).

 |  |
Another example. How, reflecting on the origin of the goods purchased in a grocery store, you can schematize the different paths that the same type of product may have done:

Then, in the following classes, the graphs will become an important tool to gradually learn the meaning of the formulas, to focus on the first conventions on the writing of terms, ... and to solve problems within the reach of pupils but which they would not be able to describe and "manipulate" by equations.
A reflection on the setting of geometric teaching in primary school should be addressed starting from some general consideration on geometric teaching, which we can entrust to this "digression", fantastic but very concrete, on the concept of angle. In it we pose the problem of how to differentiate, by formalization and "technical" development, the teaching of the various themes in the different school levels. A geometric theme has been taken as a "symbolic" reference because this area of mathematics is the one that in teaching is dealt with in a more "dissociated" way compared to the current state of the discipline.
In light of these considerations, let's see in more detail which aspects of geometric education should be addressed in the early school years. To illustrate them concretely we begin by making four examples of activities that can be carried out between the end of kindergarten and the beginning of primary school, which we describe in the form of deliveries for children.
| (1) Blindfolded children of 6 years in the first days of school make the path drawn to the side, marked by a rope fastened with adhesive tape on the floor of the school corridor. Then they describe it both in words (with phrases such as "the rope zigzagged, all the same zigzags", "it looked like a mountain, it went up and down", ...) and in drawings. Two children represent it with the drawings reproduced below. Explain in words which aspects the two children represented well and which not. |  |
| (A) |  |  |
(B) |
(2) Below you see parts of two drawings of the same field made by a 6 year old boy after two successive outings made with his class and his teacher. Which of the two drawings was made after the second release? Why?
| (A) |  |  |
(B) |
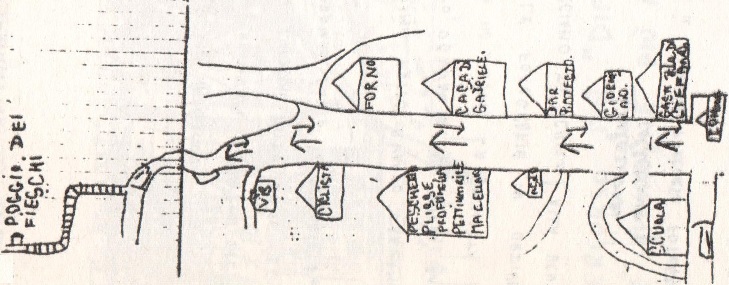
(3) The drawing of a 6-year-old boy from a village in Liguria that represents the path taken to go with the class to the "Poggio dei Fieschi" church: a piece along the way, then a climb with steps. The teacher says that in the drawing there are things seen from different points of view and asks to better explain this observation. (For teachers: a subsequent phase of class work can be the comparison with the map and/or with that of the photograph from above, recoverable via Internet; the teacher must be careful not to say "you are wrong", but must gradually focus on the different objectives of a drawing that does not want to describe only a path but also wants to convey emotions and considerations of various types, not communicable with a photograph or a geographical map)
(4) Look at the objects depicted and the "prints" below them. The tracks were obtained by pouring flour on the objects. The dimensions of the objects and of their prints are not respected in the drawing. Combine each object with its imprint. Explain in words why you made this choice. (For teachers: The association of objects with their prints is easy, especially if the pupils have done similar activities "practically", actually pouring the flour; the most significant thing, and useful for the activities that may originate from it, is the description in words of the reasons for the choice, which can be made orally or intertweaving written considerations with collective discussions)


The many images in the comments relating to all the other items highlight how this area is also intertwined with the remaining areas of mathematics. The sides of this interconnection are essentially two: on the one hand (to represent and study geometric objects) many aspects come into play: measures of distances, angles, extensions, displacements, ... and realization or study of geometric transformations involving numbers, operations arithmetics, relationships and more generally functions; on the other, to represent the other mathematical objects (from numbers to functions, up to statistics and probability), from the earliest cultural experiences (not only didactic), one use objects and geometric concepts, as we have already highlighted with many examples.
Let's take a few more examples to highlight aspects that need to be brought into focus from the early years.
• The pupils must understand what an angle is (the angle intended as a rotation with which to move from one side to the other, not as a "part of the plane" between the two sides, the way books often present it, inducing the misconception for which, in the following figure, the angle A is greater than the angle B):

• They must understand (through discussions, verbally explaining the reasoning followed) why by measuring the length of the chocolate bar shown below it is wrong to conclude that the bar is about 6 cm long.
|
• They must acquire (through experiences, observations, drawings, visualization of images obtained with a camera, ...) the ability to associate visions with points of view:
|
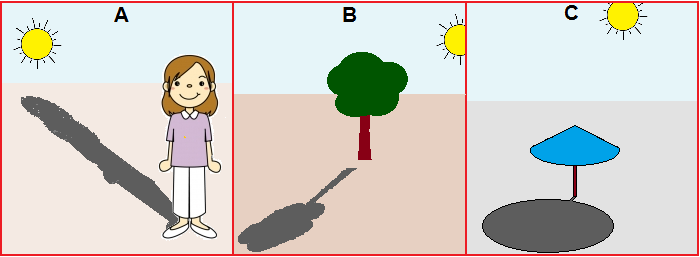
• The free-hand drawing activities (and those of drawing houses, streets, gardens, ... whose outlines are traced on transparent sheets hanging from the class windows, those of photographic reproduction, ...) are important occasions for space education , which must be significantly intertwined with other educational aspects. An important aspect is also the depiction of the shadows, which must first be freely addressed in the context of drawings invented by children and then with reflections linked to direct observations of shadows generated by the sun or a lamp, which must be followed by verification activities (or starting points for new experiences) such as explaining in words which or which of the three figures A , B and C below are wrong and why:
We defer to the considerations on the concept of "space" in the parts dedicated to subsequent school levels.
As already mentioned, the concepts will have to be taken up and deepened later, with a view to a "spiral" recovery of the topics: it is not a question of making "anticipations", but of using, in appropriate ways, terminologies and concepts that find natural intertwining with other concepts and lay the foundations for the construction of subsequent levels of formalization. This aspect seems fundamental to us, both to give a correct and "living" image of mathematics, and not to favor mental stiffenings that identify concepts with particular definitions, particular calculation procedures, ... and classify them into areas (geometry, arithmetic, ...) not communicating with each other. HERE you can find various exercises that exemplify the considerations made in this paragraph.
In the initial paragraph, on the concept of model, we discussed at length the relationships between reality and the various models, disciplinary and otherwise, with which it, or its particular aspects, can be represented and studied. We also highlighted the differences between the mathematical models and the other disciplinary models, and the didactic attentions that all these aspects must urge in those who have the task of educating the new generations, especially in the early school groups.Relations with other subject areas
In the initial paragraph, on the concept of model, we discussed at length the relationships between reality and the various models (disciplinary and otherwise) with which it, or its particular aspects, can be represented and studied. We also highlighted the differences between the mathematical models and the other disciplinary models, and the didactic attentions that all these aspects must urge in those who have the task of educating the new generations, especially in the early school levels
While the other disciplines refer to different types of phenomena, mathematics is characterized by the type of artifacts it employs and is organized on the basis of their properties and the formal relationships between them, even if some border sectors (computer science, econometrics, mathematical physics, ...) are characterized by the relationship with certain disciplines and technological areas.
But, as we have highlighted above, the birth and historical development of the various mathematical concepts has become intertwined with other knowledge, and the ability to use mathematical artifacts depends on the knowledge of the contexts in which they are used. In the long journey of scholastic and extrascholastic learning through which we become adults, things initially acquired as abstractions then become concrete "objects" to describe "reality" on which to create new abstractions. But, in order for this process to develop effectively, this concrete-abstract passage must be gradual, be "perceived" by the pupils, refer to the various cognitive aspects with which they deal in everyday life, to get there progressively to disciplined organized forms.