modello
e realtà
Su alcuni concetti / temi matematici da affrontare nella 2ª parte della scuola primaria
("intrecciati" all'interno di unità didattiche)
[scuola primaria - A primaria - B sec. 1º grado sec. 2º grado - A sec. 2º grado - B]
Il concetto di modello
Il concetto di numero
Le potenze
Le operazioni aritmetiche
I concetti di rapporto e proporzionalità
I diagrammi
Approssimazioni. Calcolatrici. Calcolatore
La statistica descrittiva
Formule, termini, grafi
I concetti di funzione e di risoluzione di un'equazione
Lo spazio
Calcolo delle probabilità
Rapporti con le altre aree disciplinari
Sono ripresi, con un taglio diverso, più o meno gli stessi contenuti presenti nel documento relativo al livello scolastico successivo;
molti temi sono comunque affrontati anche in quello relativo al livello precedente.
Le indicazioni sono riferite a quanto mediamente si dovrebbe affrontare nella seconda parte della scuola primaria.
Esse sono presentate articolate per aree tematiche ma, come via via chiarito, nei percorsi didattici i diversi concetti matematici devono
intrecciarsi tra di loro e con le altre discipline.
La matematica può essere definita la scienza dei modelli. Il concetto di modello deve dunque avere un ruolo centrale nel suo insegnamento sin dai primi livelli.
Il tema della modellizzazione accomuna tutte le forme di sapere; ciò offre numerose e feconde occasioni di interazioni tra l'insegnamento della matematica e quello delle altre discipline.
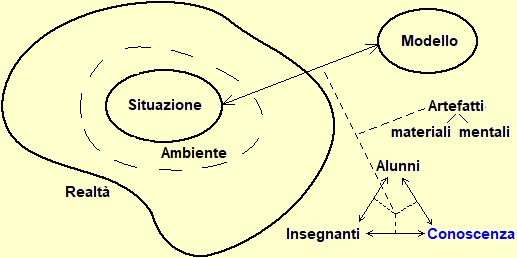
La figura seguente illustra il rapporto tra "modello" e "realtà". Data una situazione reale un modello ne è una rappresentazione semplificata che ne illustra alcuni aspetti, per certe finalità. A seconda delle finalità vi possono essere modelli differenti della stessa situazione (un modello di un aeroplano può avere la stessa forma e colore di un aereo vero ma non volare, o può non assomigliare ad un aereo vero ma volare). La "bontà" di un modello dipende dalla sua adeguatezza agli obiettivi per cui è stato costruito (per evidenziare meglio alcuni aspetti, per generalizzare alcune proprietà, per facilitare il confronto con altre situazioni modellizzate in modo analogo, …). La fase preliminare della modellizzazione circoscrive gli aspetti della realtà coinvolti nel problema che si vuole studiare. Nello schema seguente l'ambiente è la parte di realtà che viene isolata, non dettagliatamente, in questo modo, e la situazione è il complesso degli aspetti del fenomeno da modellizzare (incluse le assunzioni, le intuizioni, le percezioni, le intenzioni, … di chi costruisce il modello) di cui si vorrà tener conto nella rappresentazione:
| modello e realtà |
 |
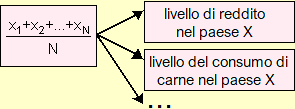
Lo stesso modello può essere impiegato per rappresentare situazioni diverse. Un esempio molto semplice è il concetto di media aritmetica, che può essere usato per indicare, in un dato paese, il consumo pro-capite di carne, il reddito medio per famiglia, l'altezza media dei ventenni, … Un altro esempio comune è la diretta proporzionalità, che può essere impiegata per rappresentare la relazione che intercorre tra il peso di un prodotto alimentare e i suo costo, tra l'allungamento di una molla e il peso dell'oggetto ad esso appeso, tra le distanze tra le parti di un'automobile e quelle tra le parti corrispondenti in un suo modellino, …
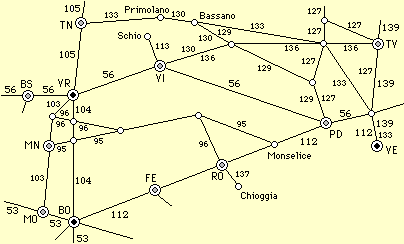
E una stessa situazione, a seconda delle esigenze, può essere rappresentata con modelli diversi. La figura sottostante a destra riproduce parte dell'indice grafico stampato nella prima pagine di un orario ferroviario: è una cartina in cui sono riprodotte le linee ferroviarie e sono indicati i relativi quadri dell'orario; essa è un modello diverso da una usuale cartina geografica in quanto non rappresenta correttamente le distanze e le direzioni.
 |  |
Vediamo un altro esempio, semplice, in cui affrontiamo un problema con due modellizzazioni matematiche differenti.
Oppure posso affrontare il problema in modo concettuale: ipotizzare che il dado sia perfettamente equilibrato e ritenere quindi che le uscite "1 e 2" abbiano 2/6, ossia 1/3 come probabilità di uscita. | 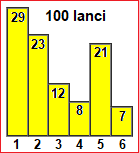 |
 | Il modello "concettuale" mi consente di trovare velocemente una risposta, però si basa sull'ipotesi che il dado sia perfettamente equilibrato (come non lo sono i dadi costruiti col cartoncino e neanche gli usuali dadi da gioco, in cui, per esempio, la faccia con "6" pesa meno della faccia con "1"). Il modello "empirico", basato su una sperimentazione col "mio" dado, mi consentirebbe, se avessi molto tempo a disposizione, di trovare una risposta più corretta (vedi la figura a sinistra); ma mi servirebbero gli strumenti probabilistici per valutarne la precisione. Poi c'è un rapporto tra i due modelli: uso il modello empirico per valutare la adeguatezza del modello concettuale. Insomma, l'uso della matematica non consiste nell'applicare brutalmente delle formule, ma comporta degli atteggiamenti culturali non "meccanici", e, al di là di questo esempio, è anche a ciò che deve educare la scuola. |
In molti casi, come in quelli ora esemplificati, occorre reinterpretare il modello verificandone l'adeguatezza a
rappresentare il fenomeno studiato ed eventualmente precisare meglio la situazione da modellizzare.
Nello schema abbiamo messo una doppia freccia
Nella figura sono presi in esame non solo i rapporti modelli-realtà ma anche gli "strumenti" impiegati per costruire i modelli e come la loro messa a punto interagisca col processo educativo, ossia con gli alunni, i docenti e il complesso delle conoscenze (le discipline, le tecniche, …).
I modelli sono rappresentazioni astratte di oggetti o fenomeni "reali" (di tipo materiale: una rappresentazione topografica è il modello di un territorio; di tipo sociale: i concetti di "verbo", "sostantivo", ... sono dei modelli per rappresentare certi elementi della comunicazione verbale; … o di tipo astratto: la "proprietà commutativa" è un modello per descrivere un aspetto di alcune operazioni matematiche).
I modelli sono costruiti utilizzando artefatti cognitivi, ossia "oggetti materiali" (carta, segni, suoni, colori, …) o "costruzioni artificiali" ad hoc (il linguaggio, i concetti, …) che l'uomo usa come protesi della sua mente. Il termine "cognitive artifact" fu introdotto da Donald Norman nel 1993 (Norman D.A., Things that Make us Smart, Wesley Publishing Company, Addison, 1993), mentre quello di "prosthesis tools" fu proposto da Jerome Bruner nel 1986 (Bruner J.S., Actual Minds, Possible Worlds, Cambridge, Mass., Harvard University Press, 1986).
La messa a punto degli artefatti cognitivi per modellizzare le situazioni non avviene episodicamente, ma in un contesto sociale di crescita culturale che viene via via ad organizzarsi in forme strutturate di conoscenza, che vengono trasmesse da una generazione all'altra attraverso processi educativi, in cui gli alunni e i docenti interagiscono tra loro e col sapere, quello in costruzione e quello consolidato. Queste reciproche interazioni sono descritte dal triangolo raffigurato in basso a destra nella figura iniziale.
Quanto osservato sin qui vale per tutte le discipline e le forme organizzate di sapere. Ma la matematica ha la specificità di non essere caratterizzata da una particolare area di problemi o di fenomeni che cerca di modellizzare (come la fisica, la storia, la linguistica, …), bensì dalla tipologia degli artefatti che impiega per la costruzione dei modelli, e che vengono utilizzati in tutte le altre discipline. Quindi lo schema grafico visto sopra (che di per sé è una semplificazione) al fine di rappresentare la situazione dell'insegnamento della matematica deve essere almeno arricchito col tratteggio verticale raffigurato a lato: gli artefatti, per la matematica, presto, da strumenti conoscitivi diventano degli oggetti di conoscenza, da modelli che "astraggono" a partire da situazioni diventano man mano degli strumenti "concreti" per mettere a punto nuove astrazioni, in una spirale senza fine. Il sapere matematico, che nasce dai contesti modellizzati, si organizza internamente non sulla base di questi, ma dei rapporti e delle analogie strutturali tra i suoi artefatti. | 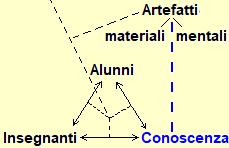 |
La situazione, poi, si fa più complessa in quanto sia il "triangolo", sia la tipologia degli "artefatti", con l'avvento dell'informatica, sono divenute più articolate: il software è diventato un interlocutore "animato" che interagisce tra i diversi soggetti, in modi molto diversi a seconda dell'uso che ne viene fatto e della consapevolezza con cui viene impiegato. Senza complicare ulteriormente la schematizzazione precedente, occorre tener presente che il software ha ora, e avrà sempre più, una incidenza decisiva nel modo in cui i diversi aspetti interagiscono tra di loro.
Riassumendo, possiamo comunque dire che lo studio della matematica si articola nel rapporto (non lineare) tra porsi problemi, modellizzare le situazioni per affrontare la soluzione dei problemi, costruire e ricorrere a teorie che organizzano internamente i rapporti tra gli artefatti impiegati per la costruzione dei modelli e mettono a punto nuovi eventuali artefatti.
Tutto ciò rende cruciale, nell'educazione matematica, il ruolo dell'insegnante. Egli deve:
• progettare e curare percorsi didattici che diano concretezza ad artefatti man mano più lontani da forme elementari di percezione,
• far emergere i conflitti realtà-concetti astratti
(da quelli tra specchi "fisici" e "matematici"
a quelli tra linguaggio "comune" e linguaggio "matematico", ad esempio quando si parla di angoli e lati o
di rettangoli, rombi, …, e ai molti altri presenti sin dalle prime esperienze di insegnamento)
che, se non esplicitati, rischiano di essere fonti di misconcezioni,
mentre, se affrontati, sono un'occasione per trasformare una "opposizione distruttiva" in una "dialettica produttiva", che contribuisca a costruire
un'immagine adeguata della matematica come disciplina,
• educare alla scelta dei modelli (non esiste "il" modello migliore) a seconda delle esigenze e delle "risorse" (artefatti fisici e concettuali) disponibili,
• organizzare l'insegnamento in modo che i riferimenti ad oggetti o situazioni reali non siano solo dei pretesti ma instaurino
dei rapporti virtuosi con le conoscenze (e le motivazioni) extra-scolastiche degli alunni, decentrando, cercando di aver come riferimento
non solo le proprie conoscenze e le proprie motivazioni ma, in un rapporto dialettico, anche quelle degli alunni,
• e dare organicità alle conoscenze da loro man mano acquisite in campo matematico
(anche affiancando allo studio di situazioni problematiche la messa a punto - a partire da esse - di nuovi concetti e
il consolidamento di alcune abilità operative attraverso opportuni esercizi,
che dipendono dal livello delle conoscenze e delle tecnologie storicamente disponibili)
in modo che diventino un solido terreno di partenza per nuove astrazioni,
• tenendo conto che, specie nei primi livelli di istruzione, la costruzione di rapporti virtuosi con l'extra-scuola
dipende anche dal coinvolgimento delle "famiglie": occorre farle partecipare "culturalmente" al progetto educativo che si sta portando avanti
(partecipare "culturalmente" non vuol dire "fare i ripetitori", ma collaborare con i docenti nella costruzione di rapporti tra le attività
scolastiche e la vita extrascolastica); questo è uno dei compiti più difficili; anche questo aspetto andrebbe opportunamente inserito
nel "triangolo didattico" considerato sopra …
QUI trovi qualche esempio che illustra i "i limiti dei modelli".
Questo è un aspetto, accennato anche in precedenza (quando abbiamo osservato che una stessa situazione può essere rappresentata
con modelli diversi) e che viene ripreso anche in punti successivi, a cui è assai importante dare rilievo nell'insegnamento.
Le prime tre delle immagini seguenti illustrano alcuni aspetti (concettuali e pratici) della padronanza numerica che dovrebbero essere stati avviati negli anni precedenti: l'uso dei numeri per contare, rappresentare e operare con valori monetari, leggere e rappresentare grandezze utilizzando strumenti di misura di uso quotidiano, fino a prime rappresentazioni sulla linea del tempo (ad esempio per segnare eventi accaduti durante il mese o durante l'anno). Nella seconda parte della scuola primaria ci si può estendere a leggere e rappresentare eventi su una linea del tempo più "lunga" (dapprima fino all'epoca dei bisnonni, poi spostandosi indietro negli anni).
 | |||
| CLICCA QUI |
 |
 |
|

Un quarto d'ora quanti minuti sono? E tre quarti d'ora?
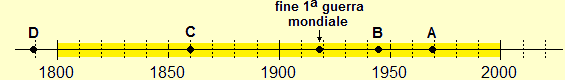
Attraverso il riferimento agli usi quotidiani del numero, si devono sviluppare alcune abilità di
scrittura ed elaborazione numerica, si deve consolidare l'abitudine a fare (implicitamente) dei transfert
da un contesto all'altro per interpretare alcune semplici operazioni (problemi quantitativi tradotti in problemi sulla linea dei numeri
o viceversa) e, a seconda dei casi, ad operare ad esempio su divisioni ragionando per contenenza (200/50 fa 4 in quanto 50·4 = 200)
o per partizione (200/4 fa 50 in quanto dividendo 200 in 2 parti ottengo 100 e dividendolo ulteriormente in 2 parti ottengo 50) anche se
i problemi concreti affrontati con esse erano, rispettivamente, di partizione o di contenenza.
Si deve avviare, a partire dai più vari contesti, alla interpretazione dei numeri "astratti" come posizioni sulla retta graduata,
che dovrà poi essere consolidata nella scuola secondaria di 1º grado: è uno tra i pochi automatismi (di elaborazione, associazione,
passaggio da una rappresentazione a un'altra, ...) che tutti dovranno saper esercitare senza sforzi mnemonici o riflessivi
(per liberare risorse mentali da dedicare ad aspetti più concettuali); sono abilità/atteggiamenti che è opportuno consolidare/mantenere allenati continuamente.
È opportuno anche far riflettere gli alunni sulle ambiguità con cui, nel linguaggio verbale, vengono espressi i numeri con "punto", ossia i numeri con "virgola", oltre a far notare (ad es. osservando il menu-opzioni di un computer o di un cellulare) le diverse convenzioni ("," e ".") che, in ambito commerciale e nella vita quotidiana, si usano da una parte in Italia, dall'altra nei Paesi Anglosassoni e nel mondo scientifico, per separare la parte intera da quella frazionaria.
| Il punto (o la virgola) decimale nel linguaggio orale viene letto spesso "e"; ad esempio "1.23" viene letto "uno punto ventitré" o "uno e ventitré", oltre che "uno e ventitré centesimi"; di fronte a "5.03", se non si aggiunge "centesimi", occorre dire "cinque e zero tre", per evitare di confonderlo con "5.3". Nei dialoghi quotidiani spesso si usano convenzioni diverse a seconda del contesto in cui ci si trova. Ad esempio parlando di automobili, con "cilindrata mille e tre" non intendiamo 1003, ma 1300, ossia "mille e trecento"; in altre parole si sottintende il "cento". Parlando di soldi, con "un euro e tre" in genere si intende 1.03 €, ossia "un euro e tre centesimi", non 1.3 € (ossia "un euro e trenta centesimi"). |
Intrecciate al consolidamento del concetto di "numero" sono le prime riflessioni sulle potenze, sul calcolo approssimato, sulla linea dei numeri (e sui numeri negativi), … a cui si accenna nei successivi commenti.
La padronanza dei numeri decimali limitati, la capacità di utilizzare strumenti di misura graduati, … sono fondamentali, in particolare, per avviare, informalmente, al concetto di numero illimitato (che verrà ripreso nella scuola secondaria di 1º grado e che in quella di 2º grado verrà chiamato anche numero reale).
Senza una prima messa a punto del concetto di numero illimitato non avrebbe alcun senso l'uso delle radici quadrate (non esisterebbe alcun un numero che al quadrato faccia 2) né, ad esempio, l'uso di π. Né avrebbero alcun senso gli esercizi di geometria "astratti", in cui i lati o gli angoli abbiano delle misure "esatte". Occorre poi, in modo semplice, senza formalismi, mettere a fuoco che si fanno degli esercizi con delle misure esatte per semplificarsi la vita senza tener conto delle approssimazioni, ma che in realtà non esistono oggetti di cui si possa misurare la lunghezza con esattezza (vedi questa animazione):
 |
E occorre mettere a fuoco, sempre senza formalismi, che mentre le lunghezze di oggetti non hanno i contorni precisi, nel caso dei tempi non abbiamo queste limitazioni: il tempo varia con continuità, non a scatti. Siamo noi che non possiamo misurarlo esattamente.
Non è il caso di soffermarsi su come si possano fare somme e prodotti di numeri decimali illimitati o di come si possa calcolare la radice quadrata di un numero, su cui ci soffermerà in classi successive.
Non ha, ovviamente, alcun senso (né "didattico", né "culturale") affrontare in generale il calcolo in basi di numerazioni generiche.
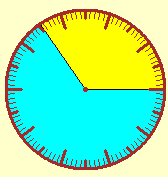
Altra cosa è avviare all'uso delle notazioni numeriche
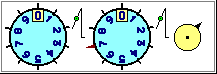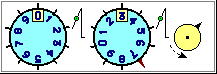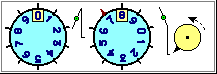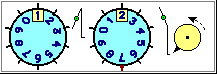
impiegate nella misura dei tempi (basi 12, 24, 60), sulle quali gli alunni hanno già competenze operative
acquisite gradualmente nel corso della loro vita (vedi la figura all'inizio di questa voce), e da cui occorre partire
facendo riferimento, operativamente, ai concetti di "rapporto" e di "cambio" di unità di misura.
Nella scuola primaria l'uso delle potenze deve essere avviato in relazione alle misure di aree e volumi: si apprende, operativamente, che in 1 decimetro ci stanno esattamente 10 centimetri e che in 1 decimetro cubo ci stanno esattamente 1000 centimetri cubi, e che non a caso 1 centimetro cubo è 1 millilitro, essendo 1 litro pari a 1 decimetro cubo.
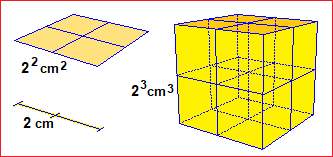
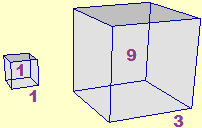
| Occorre mettere a fuoco l'utilità delle potenze non solo in relazione all'uso di unità di misura diverse, ma anche alla graduale educazione all'uso delle calcolatrici tascabili. Sull'uso della notazione esponenziale per descrivere numeri grandi e piccoli si tornerà nella scuola secondaria. |  |
Abbiamo già discusso su come dovrebbero essere avviate le prime forme di calcolo discutendo dei numeri, che inevitabilmente possono essere introdotti solo contestualmente all'esercizio di qualche attività di calcolo (abbiamo messo in luce come per parlare dei "numeri" è inevitabile parlare delle "operazioni", abbiamo discusso dei rapporti tra le divisioni per contenenza e quelle per partizione, …).
La formazione della capacità di operare con i numeri va fondata su modelli concreti e strettamente collegata a situazioni problematiche; ciò non a scapito dell'acquisizione di una padronanza degli algoritmi, ma per una loro acquisizione meno superficiale e più duratura.
Val la pena di ricordare che con modelli concreti non si intendono affatto i cosiddetti "materiali strutturati", che sono un tipico esempio di modelli astratti. Situazioni problematiche che abbiano riferimento alla realtà, e che, per altro, offrano occasioni di manipolazione di materiali che abbiano concretezza e ricchezza di contenuto matematico (e in questo senso siano "strutturati"), ve ne sono molte: operazioni di misura con grandezze fisiche, analisi di dati economici e demografici, …, attività di natura geometrica e statistica, …, oltre alle molteplici altre opportunità offerte all'insegnante dai temi e dalle attività che affronta con la propria classe.
Un altro suggerimento è quello di limitare il numero delle cifre impiegate nei calcoli
privilegiando l'acquisizione e il consolidamento della notazione posizionale e dei "cambi". I modelli concreti, sia
attraverso attività pratiche (es. lavorare con monete e banconote, con misuratori di capacità, lunghezze, … ),
sia, poi, attraverso riferimenti verbali e grafici (illustrare graficamente e verbalmente situazioni di scambio economico, attività
di misurazione, …), possono essere di aiuto nella limitazione e isolamento delle cifre che effettivamente entrano in gioco nei
calcoli e nella focalizzazione dell'idea dei cambi: per sommare 15 centesimi e 20 centesimi o sommare 200 euro e 300 euro
non devo fare una somma tra numeri espressi in centesimi o in centinaia, ma, usando l'unità "centesimo" o "cento euro",
posso fare 15 centesimi e 20 centesimi = 35 centesimi o 2 cento euro + 3 cento euro = 5 cento euro; suddividere un
litro di latte in tre parti non comporta una divisione in cui intervengono cifre decimali se si considera che 1 l = 1000 ml
e si fa 1000:3, eventualmente trasformando poi il risultato in litri; o per fare trenta centesimi per 5 si può fare
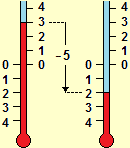
Attività di questo genere, oltre a consentire di svolgere calcoli concettualmente alla portata degli alunni senza man mano attendere l'intervento di nuove regole e tecniche "magiche" che consentano di affrontare i numeri più "difficili", sviluppano la competenza numerica e la padronanza "operativa" delle proprietà aritmetiche (possibilità di riordinare una somma o un prodotto, distributività, moltiplicazioni e divisioni per 10, 100, …). Una volta che tali abilità si sono consolidate nei "contesti", è più facile, grazie alla presenza di questi modelli di riferimento che fungono da "prototipi" concettuali, trasferirle alle attività con i numeri puri. Considerazioni simili valgono per l'introduzione dei numeri relativi appoggiandosi a situazioni significative (temperature, piani degli ascensori, livello di fiumi, differenza temporale rispetto a un giorno o a un'ora fissata che da "futuro" diviene poi "passato", … ).
 |
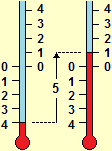 |
| La temperatura passa da −4° a 1°: sale di 5°. |
Contestualmente al suggerimento di non svolgere precocemente calcoli per iscritto che comportino troppe cifre, si sottolinea l'opportunità di sviluppare gradualmente le tecniche di calcolo, di cui gli alunni devono essere messi in grado di comprendere il significato. Nelle figure seguenti sono esemplificati alcuni possibili sviluppi (successivi a quelli esemplificati dalle figure della voce "il concetto di numero") attraverso cui si possono introdurre alcune tecniche.
 |
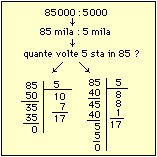 | 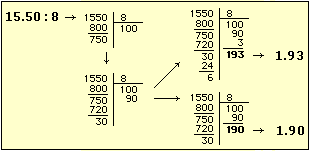 |
Alcune animazioni
|
Tecniche di calcolo che impieghino schematizzazioni simili a quelle sopra
illustrate possono costituire un passaggio intermedio per un'introduzione motivata di procedimenti più "automatici",
ma possono essere impiegate pure in seguito: oltre ad essere più "controllabili" di questi ultimi, in molti casi sono anche
più efficaci. Infatti esse non prevedono uno sviluppo univoco, ma consentono di procedere in modi differenti a seconda delle
caratteristiche dei numeri coinvolti (e dei gusti del soggetto che esegue il calcolo). Attività di questo genere e, più in
generale, l'impiego di algoritmi differenti per ottenere un medesimo risultato sono assai importanti. Ovviamente occorre consolidare "mnemonicamente" la tabellina della moltiplicazione. C'è chi trascura questo aspetto, c'è chi ricorre a buffe strategie di memorizzazione (c'è un ampio repertorio di strambe tecniche e trucchi), ma non c'è altro modo che fissare nella mente, anche attraverso attività ripetitive, facili da motivare, e che possono facilmente integrarsi con l'uso delle calcolatrici e col calcolo mentale rapido (a cui accenniamo più avanti), i risultati di queste (64) moltiplicazioni. |
|
Accenniamo, rapidamente, ad altre attività collegate: diverse descrizioni dello stesso algoritmo (formule diverse, grafi di flusso, …), calcolo approssimato, attività statistiche, attività con basi diverse (usate nella "vita") che possono essere offerte dalle attività di misurazione e di uso di grandezze fisiche (il tempo, le rotazioni).
Rinviamo a questi esercizi, e a quelli presenti nelle pagine successive, per ulteriori idee.
Occorre poi tener presente l'eventuale presenza di alunni con disturbi di tipo discalculico o dislessico. Per questo problema rinviamo alle considerazioni svolte QUI nella sezione dedicata alla scuola secondaria di 1º grado.
Le operazioni aritmetiche sono le prime funzioni numeriche con cui si ha a che fare nella vita scolastica. Su questo torneremo più avanti.
I concetti di rapporto e proporzionalità
I concetti di rapporto e di proporzionalità vengono costruiti progressivamente nell'ambito di ogni attività di matematizzazione; lo abbiamo già visto nelle voci considerate nei punti precedenti (quando si fa uso di unità di misura differenti, quando ci riferisce all'impiego dell'orologio, …). I concetti vengono costruiti in contesti in cui si intrecciano l'uno con l'altro; poi, gradualmente, la scuola dovrebbe metterne in luce le differenze e le relazioni di analogia.
Tra i contesti affrontando i quali si possono sviluppare questi concetti ve ne sono molti riferibili a tematiche storiche, tecnologiche o geografiche, sviluppate anche nel corso di visite ad aziende. Si pensi, ad esempio, alle osservazioni sulle forme e sul funzionamento di macchinari (eventualmente utilizzabili anche per attività produttive affrontabili a scuola), …; ad esempio una macchina che tira le sfoglie, che divide per 3 lo spessore e moltiplica per 3 la lunghezza della sfoglia, un frullino con la ruota azionata che ha il quadruplo dei denti di quelle delle fruste, un mulino in cui il rapporto tra i pioli delle due ruote che ingranano è pari al rapporto tra le velocità di rotazione della ruota a pale azionata dall'acqua e di quella della mola:
|
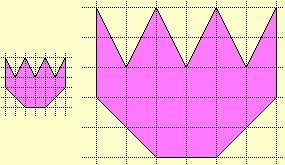
Altri contesti consentono di mettere a fuoco l'idea di trasformazione proporzionale: se dimezzo le dimensioni di un rettangolo il rapporto tra di esse non cambia (b), se cambio le unità di misura il rapporto tra le misure non cambia (a); e il rapporto tra due numeri non cambia se li moltiplico o divido entrambi per lo stesso numero. Questa è la conclusione a livello adulto: gli alunni devono arrivare (attraverso attività nei vari contesti) a padroneggiare operativamente (non a recitare) questa proprietà.
|
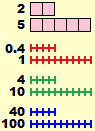 |
Nella scuola scuola secondaria di 1º grado la padronanza di questi concetti dovrà poi trovare modi più formali di consolidamento. Ma già nella scuola primaria gli alunni devono acquisire gradualmente la capacità di passare "in modo spontaneo" da una forma di rappresentazione all'altra dei rapporti d'uso più comune (0.75, 3/4, 75%, 45/60; 15/60, 1/4, 25%; 1/3, 20/60, 0.333…, 33%; …), anche attraverso esercizi che ne consolidino le varie rappresentazioni grafiche (diagrammi a striscia, a settori circolari, opportunamente graduati). Devono padroneggiare l'equivalenza tra divisione per contenenza e per partizione per rendersi conto immediatamente, ad es., che 1/0.1 è 10 in quanto 0.1 sta 10 volte in 1. Devono acquisire l'idea che "%" sta per "/100".

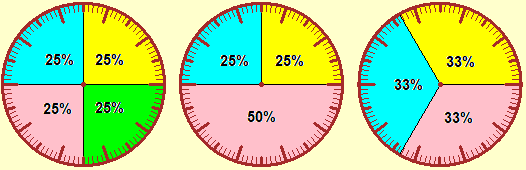
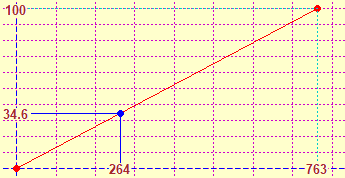
L'intreccio con le rappresentazioni grafiche è importante anche per esprimere in forma percentuale i rapporti:
per il rapporto tra 264 e 763 (dati riferiti a qualche contesto) possiamo
ricorrere a rappresentazioni grafiche prima su carta millimetrata (vedi) poi, eventualmente, utilizzando anche del software (vedi la figura sotto a sinistra),
senza necessariamente passare al calcolo numerico, che, verso la fine della scuola primaria, potrà essere effettuato con una calcolatrice (fare la divisione ed esprimere
il risultato in centesimi: 264  763
763  100
100  ).
In particolare occorre far osservare che il simbolo
":" (che compare sulla carte geografiche) è semplicemente il
simbolo di divisione, e che questo può essere espresso anche con "/", e che, ad esempio, per trovare l'angolo
con cui esprimere 264 se 763 viene rappresentato con l'intero cerchio, posso,
come visto nelle figure precedenti, usare un cerchio diviso in 100 parti.
).
In particolare occorre far osservare che il simbolo
":" (che compare sulla carte geografiche) è semplicemente il
simbolo di divisione, e che questo può essere espresso anche con "/", e che, ad esempio, per trovare l'angolo
con cui esprimere 264 se 763 viene rappresentato con l'intero cerchio, posso,
come visto nelle figure precedenti, usare un cerchio diviso in 100 parti.
 |  |

Il concetto di frazione è bene che sia presentato come un caso particolare di rapporto: questo consente di intrecciare bene i diversi aspetti con cui le frazioni si presentano nelle applicazioni. I contesti in cui si impiega il concetto di rapporto sono innumerevoli; oltre a quelli considerati in precedenza richiamiamo ad esempio i rapporti di trasmissione di una bicicletta, la piantina in scala di un appartamento (in cui inizialmente posso rappresentare 1 metro con 5 o 10 quadretti), … Ma anche per interpretare il significato di un cartello stradale o fare prime riflessioni sulle pendenze legate ad esempio alle esperienze di scoutismo. È bene prestare attenzione, soprattutto nella scuola primaria, a non confondere il significato di numero con quello di termine, che verrà messo a fuoco nei livelli scolastici successivi, e a non chiamare "numeri" le frazioni. Ad esempio mentre 6 o 1.333… possono essere chiamati "numeri", 2/3 (come 2+3 o 2·3) ha come risultato, o come valore, un numero ma non è un numero. Ed è opportuno utlizzare le frazioni solo per esprimere rapporti tra grandezze o quantità riferite a dei contesti concreti, mentre le attività con quelli che noi chiamiamo "numeri puri" andrebbero affrontate in relazione a prime attività sulla linea dei numeri (come quelle viste sopra), da consolidare nei livelli scolastici successivi, o all'esecuzione di calcoli, a mano o con la calcolatrice. Queste considerazioni non sono "puristiche", ma sono da riferire alle misconcezioni che, indirettamente, si rischia di creare negli alunni.
L'uso delle varie rappresentazioni grafiche facilita notevolmente i ragionamenti. È anche il modo attraverso cui le elaborazioni matematiche (relative a indagini sociologiche, situazioni economiche, fenomeni tecnico-scientifici, …) ci vengono in genere comunicate dai mass media. È quindi fondamentale che l'insegnamento educhi al loro uso (sia per modellizzare situazioni che per svolgere considerazioni teoriche), al transfert tra esse ed altre forme di rappresentazione, all'intreccio tra metodi grafici e metodi simbolici e numerici, ... Approfondimenti specifici sul piano cartesiano e sulle curve potranno essere avviati successivamente, alla fine della scuola secondaria di 1º grado.
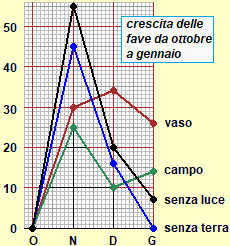
Le immagini seguenti danno un'idea delle attività a cui si può intrecciare l'uso delle rappresentazioni grafiche. I grafico seguente e il primo dei grafici successivi sono relativi ad attività che possono essere svolte nei primi anni della scuola primaria.
| |
| ore di luce e di buio registrate settimanalmente da dicembre a luglio |
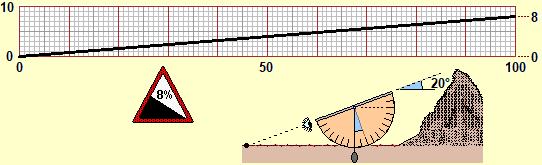
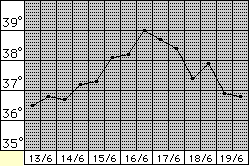
Le altre rappresentazioni sono alcuni esempi delle varie attività svolgibili negli ultimi anni della scuola primaria (osserviamo il grafico di una tappa del Giro d'Italia, del tipo di quelli che compaiono alla televisione - "la pendenza delle strade è quella dei disegni?"; leggiamo il grafico della temperatura corporea di una persona ammalata; ingrandiamo o rimpiccioliamo una figura), inserite in attività specifiche (passa il Giro d'Italia vicino alla scuola; in questo mese molti sono stati malati con la febbre alta; facciamo delle piantine dell'aula o facciamo delle fotoriduzioni o …).
 |
|
Queste brevi considerazioni vanno intrecciate con le numerose altre sulle rappresentazioni grafiche svolte nelle altre voci del documento.
Approssimazioni. Calcolatrici. Calcolatore
Abbiamo già accennato alle approssimazioni verso la fine della sezione dedicata al "concetto di numero". L'aspetto importante da mettere a fuoco è che non si possono ottenere misure esatte di lunghezze, tempi, aree, …, ma solo dei valori approssimati: non ha senso scrivere molte cifre come risultato di un problema concreto pensando di rappresentare così esattamente la soluzione. Ovviamente, in questo livello scolastico, bisogna limitarsi ad approssimare il risultato finale ad un ordine di grandezza significativo in base al contesto, senza riflessioni matematiche troppo sofisticate, pensando al significato concreto delle cifre che si considerano. Se ho dei valori monetari dovrò approssimarli agli euro o ai centesimi, per eccesso o per difetto, a seconda dei contesti. Se ho un'asta lunga 48.5 centimetri e devo dividerla in tre parti eguali, arrotonderò il risultato a 16.2 centimetri. Se voglio esprimere l'altezza di un edificio dirò che è alto, ad esempio, circa 12 metri, senza considerare i centimetri. E se eseguo le operazioni con una calcolatrice, alla fine (e solo alla fine) dovrò arrotondare il risultato tenendo conto della natura del problema. E devo imparare a leggere le misure su un nastro misuratore, su una bilancia a molla, su un orologio, …
Dobbiamo sviluppare queste "attenzioni" sin dai primi anni di scuola, se vogliamo dare un senso all'insegnamento della matematica. Poi una trattazione più rigorosa verrà effettuata nei vari livelli scolastici successivi.
Bisogna anche incominciare a fare delle stime (senza calcolatrice, a mano o a mente) del risultato di calcoli di cui non ci interessi avere il risultato esatto o per controllare i calcoli fatti per esteso. Ecco un paio di esempi di calcolo approssimato svolti arrotondando i numeri a 1 o 2 cifre significative ed eseguendo i calcoli sui valori arrotondati, affrontabili verso la fine della scuola primaria:
|
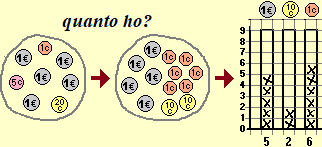
È opportuno, sin dalla scuola di base, fare un ampio uso delle calcolatrici tascabili (CT). Può essere utile all'insegnante fare una rassegna delle CT di cui dispongono gli alunni. Ricordiamo che l'uso delle calcolatrici è indispensabile nel caso siano presenti alunni con difficoltà di tipo discalculico, come ricordato nel link presente nella voce le operazioni artimetiche.
Gli obiettivi dovrebbero essere sia quello di acquisire una maggiore
padronanza di questo mezzo di calcolo, comprenderne i limiti al fine di interpretare i risultati che fornisce, …, sia quello
di introdurre e/o consolidare (a un primo livello) alcune conoscenze matematiche: sui numeri (approssimazioni, …),
sulle operazioni (proprietà, priorità, …),
sulle funzioni (funzioni ad 1 input e 1 output, come  ,
,  , …,
a 2 input e 1 output, come
, …,
a 2 input e 1 output, come  ,
,  ,
,  ,
,  ,
,
 , …, 2 input e 2 output, come
, …, 2 input e 2 output, come  , …, e composizione di
funzioni, …), …, sia quello di preparare il terreno per la comprensione del funzionamento dei calcolatori (che, come
"conoscenze" matematiche e possibilità di calcolo aritmetico, non si discostano "essenzialmente" da una CT, dove abbiamo la
possibilità di operare con i tasti
, …, e composizione di
funzioni, …), …, sia quello di preparare il terreno per la comprensione del funzionamento dei calcolatori (che, come
"conoscenze" matematiche e possibilità di calcolo aritmetico, non si discostano "essenzialmente" da una CT, dove abbiamo la
possibilità di operare con i tasti  ,
,  ,
,  , …).
, …).
|
È evidente come l'uso dei mezzi di calcolo sia da introdurre contestualmente
alla trattazione degli altri temi matematici, pur con degli approfondimenti specifici. Esempi di attività in questa
direzione affrontabili alla fine della scuola primaria possono essere suggeriti dagli esercizi presenti
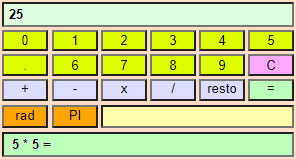
QUI. Qualche esempio di software di vario genere si può trovare QUI. Due esempi sulla destra, "divisione" e "calcolatrice tascabile" (impiegabile sin dai primi anni di scuola). Altri esempi commentati di programmi esguibili online QUI. |
 |
 |
| La statistica descrittiva, a cui abbiamo accennato più volte discutendo dei temi precedenti, e in particolare alla voce i concetti di rapporto e proporzionalità, si presta all'introduzione in contesti significativi di molti concetti matematici di base, dai numeri alle approssimazioni, dal concetto di funzione alle rappresentazioni grafiche di relazioni numeriche. Questo, almeno, se la statistica, che più di 20 mila anni fa ha costituito la prima attività di matematizzazione dell'uomo (l'uso delle "tacche" per confrontare quantità di giorni, oggetti, persone, …) e può essere affrontata sin dalla scuola dell'infanzia, non viene ridotta ad essere un tema in più da insegnare separatamente dagli altri temi. Gli strumenti di statistica descrittiva servono poi come punti di riferimento per la successiva introduzione alla probabilità. QUI sono presenti link a programmi impiegabili per elaborazioni statistiche. | 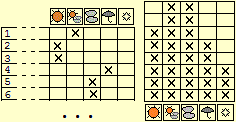 |
| La figura precedente si riferiva ad una tipica attività affrontabile nella scuola dell'infanzia (nell'ultimo anno della scuola dell'infanzia si possono registrare su un tabellone le condizioni del tempo e poi si può costruire mese per mese l'istogramma relativo), e che può essere affrontata anche all'inizio della scuola elementare, aggiungendo altre informazioni oltre a quelle meteorologiche (le assenze, annotazioni scritte su fatti significativi, …). La figura a fianco rappresenta i modi in cui gli alunni di una classe arrivano a scuola (tutti, e i maschi e le femmine), con un istogramma a cui si affiancano i numeri che esprimono le altezze delle colonne, impiegabile all'inizio della scuola primaria. | 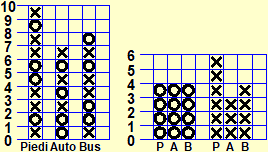 |
| Poi si possono affrontare molte altre attività, integrate all'interno di percorsi didattici che coinvolgono altri "saper fare". Un esempio: un'indagine sulle precedenti generazioni a quella degli alunni. |
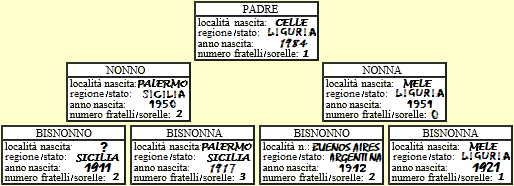
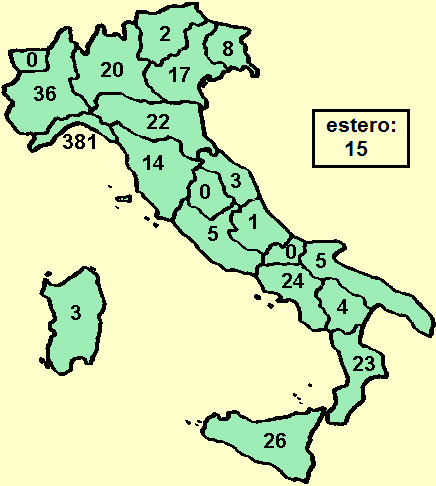
| Si tratta di un'analisi, sviluppabile attraverso la somministrazione e l'analisi di un questionario, che si può estendere a varie generazioni precedenti (qui si arriva ai bisnonni), all'interno di un percorso per costruire il senso della "storia" e della "documentazione" che può essere affrontato ad esempio in una classe terza di scuola primaria, e su cui si può lavorare anche in anni successivi. La raccolta di informazioni sulle generazioni precedenti può coinvolgere anche più classi della stessa scuola, che poi possono confrontare e mettere insieme i dati e l'altro materiale (foto, quaderni, filmati, …) raccolto. | 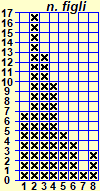 | 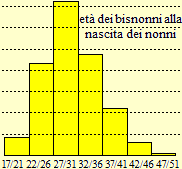 |
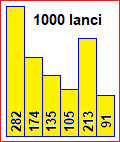
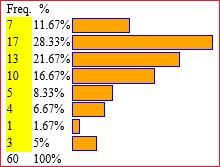
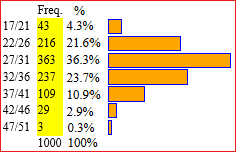
| Gli aspetti quantitativi possono essere analizzati attraverso grafici, istogrammi a crocette e, poi, utilizzando anche le percentuali (come abbiamo visto. discutendo del concetto di rapporto). A lato, ad esempio, un istogramma sul numero dei figli dei bisnonni e, a destra, quello della distribuzione percentuale dell'età dei bisnonni all'epoca all'epoca della nascita dei nonni. | ||
| Dopo che gli alunni hanno imparato a costruire istogrammi a crocette, alla fine della scuola elementare possono essere avviati ad usare semplici programmi, come questo o questo, che posso essere usati online. |
 |  |
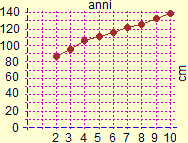
Sotto a sinistra il grafico delle altezze mediane degli alunni di una classe quinta da quando avevano due anni a quando ne hanno raggiunto dieci (vedi qui). A destra il grafico dell'andamento della popolazione italiana rilevato ai censimenti.
| Altezza mediana in varie età |
 | Popolazione italiana ai censimenti |
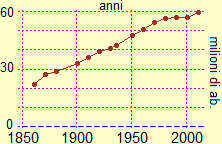 |
Le figure seguenti richiamano l'uso di diagrammi a barre e areogrammi per rappresentare classificazioni in generiche classi, non in intervalli numerici. Sono diversi modelli matematici dello stesso fenomeno (realizzabili su carta millimetrata e su cerchi graduati in centesimi), quantificabili con delle percentuali, che comunicano visivamente informazioni differenti (i primi consentono di confrontare rapidamente, in modo sia visivo che numerico, le diverse frequenze percentuali; i secondi di capire quale rapporto c'è tra le varie parti e il totale).
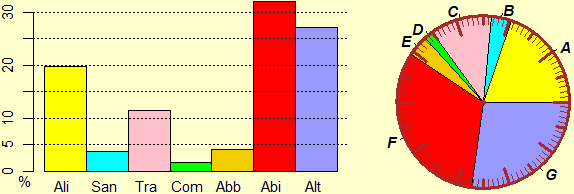
Liguria -
Alimentari Sanità Trasporti Comunicazione Abbigliamento Abitazione Altro
Gli esempi che stiamo vedendo mettono in luce un altro aspetto: la statistica deve far riferimento inevitabilmente a dei contesti non matematici, ed è quindi uno stimolo (per gli alunni e per i docenti) all'interazione con le altre discipline, oltre che a quella tra le diverse aree della matematica.
La statistica consente anche di mettere bene a fuoco come, a seconda di quello che interessa, per lo stesso fenomeno si possono considerare modelli matematici differenti che mettono in luce o trascurano aspetti diversi, come abbiamo osservato anche sopra. Non esiste il modello migliore.
A questo proposito facciamo alcune osservazioni sui concetti di media e di mediana.
Si tratta di concetti non banali la cui acquisizione (che, assieme a quella delle percentuali, proseguirà nella scuola media)
è bene avvenga gradatamente, senza precoci formalizzazioni. Si pensi ad esempio alle differenze tra situazioni come il calcolo
del consumo medio di latte, zucchero, … in cui è dominabile l'introduzione della media aritmetica come modo per esprimere
come si ripartirebbe la totalità dei consumi se vi fosse una suddivisione in parti uguali e situazioni come quella del calcolo
di una età media o di una altezza media: mentre si può parlare di "consumo totale" non ha senso parlare di "età totale" o di
"altezza totale".
Ciò suggerisce che il concetto di media aritmetica è bene che sia introdotto ad esempio per la comprensione
di dati relativi al cambiamento nei consumi di alcuni generi alimentari nell'ultimo secolo piuttosto che per valutare i cambiamenti
antropometrici degli alunni: ad esempio (come abbiamo già osservato) le altezze degli alunni in età diverse possono inizialmente
essere confrontate costruendone ed esaminandone gli istogrammi relativi alle varie età o, invece che calcolando e comparando
le altezze medie, confrontando i "valori mediani", cioè i valori che stanno al centro negli elenchi ordinati delle altezze relative
alle varie età (se, per fare un esempio relativo a pochi dati, i valori in centimetri sono ordinatamente:
Mario 108, Lucia 112, Enrico 112, Aida 118, Giorgio 120, il valore mediano è quello relativo a Enrico, cioè 112);
non si tratta di un escamotage didattico: ad esempio nelle statistiche ufficiali sui cambiamenti nella popolazione italiana si trovano
i dati relativi alla età mediana di morte (se l'età mediana di morte in un certo anno era 42 anni,
ciò significa che il 50% dei morti avevano età non superiore a 42 anni e l'altro 50% età non inferiore a 42 anni).
Nella scuola primaria occorre introdurre l'uso dei "grafi ad albero", importante per imparare gradualmente il significato delle formule e a passare da un linguaggio all'altro, per mettere a fuoco le prime convenzioni sulla scrittura dei termini, … e per descrivere procedimenti non facilmente descrivibili come formule, per risolvere problemi, ...
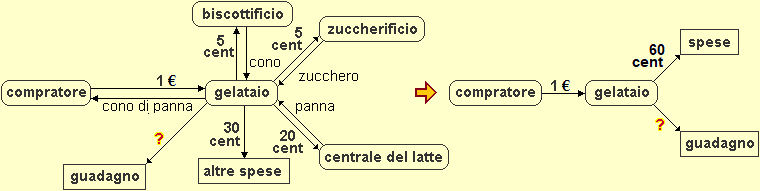
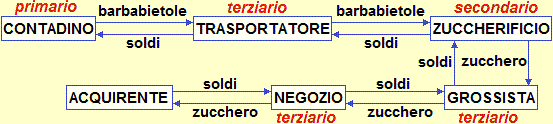
Essi, per altro, sono usati in varie altre discipline: l'immagine sotto a sinistra ne richiama un tipico impiego. L'immagine a destra ne richiama un uso particolare in ambito matematico, importante per mettere a fuoco la struttura dei termini.

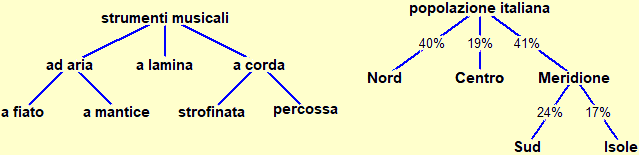
Le figure seguenti ne illustrano altri esempi tipici fatti in vari ambiti, che hanno forti intrecci con l'educazione matematica: la ripartizione in parti percentuali, la partizione di una classe in sottoclassi (da affrontare operativamente, non con riflessioni astratte sugli "insiemi").
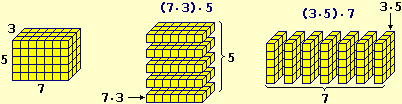
Occorre, poi, consolidare, mediante immagini e pratiche, la possibilità di riordinare i termini di una somma o di un prodotto:
Infine, impiegando metodi grafici si possono affrontare "problemi algebrici" che sono concettualmente alla portata degli alunni, senza ricorrere a "tecniche algebriche" utilizzabili in livelli scolastici successivi. Un esempio:
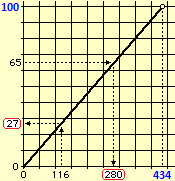 |
Quale "percentuale" di 434 è 116? |
I concetti di funzione e di risoluzione di un'equazione
I concetti di funzione ed equazione sono forse i concetti più importanti della matematica; si intrecciano con quasi tutte le altre voci qui discusse. Essi sono presenti nei programmi di tutti i livelli scolastici. Le prime funzioni che i ragazzi incontrano esplicitamente sono, all'inizio della scuola elementare, le quattro operazioni (a due input), gli incrementi e decrementi unitari e il cambio segno (ad un input). Ma alla scuola elementare incontrano anche funzioni con quantità qualunque di input, come il massimo e il minimo di un insieme di dati, e funzioni a cui non corrisponde un procedimento di calcolo (per esempio la altezza o il peso di una persona, o la popolazione di una città, al passare del tempo, o tariffari di vario genere, in cui il valore monetario è espresso in funzione di varie grandezze). Incontrano anche funzioni a più output (la divisone con resto, per esempio, è una funzione a due input e due output).
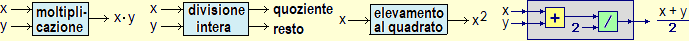
Del resto sono funzioni anche gli istogrammi a crocette, che possono essere affrontati anche prima della scuola elementare, nella scuola dell'infanzia, come quelli presenti QUI: ad ogni modo di arrivare a scuola viene associato il numero (rappresentato da una colonna di di crocette) degli alunni che lo utilizzano, ad ogni tipo di località delle vacanze viene associato il numero degli alunni che le ha passate in quel modo, ad ogni condizione del tempo viene associato il numero dei giorni del mese in cui il tempo è stato tale, …
Ricordiamo che il nome "operazione" è un appellativo usato per indicare alcune funzioni, in genere ad 1 o 2 input, ma non solo. Anche sulle calcolatrici tutti i tasti per eseguire calcoli ad 1, 2 o più input sono chiamati "tasti funzione".
Il modo più semplice e più "pulito" per introdurre una prima descrizione del concetto di funzione è proprio quello di far riferimento a immagini grafiche come quelle presentate all'inizio di questa voce e all'idea di mezzo di calcolo: le funzioni sono dei modi di associare degli input a degli output. Poi, in livelli scolastici successivi, questo concetto potrà essere messo meglio a fuoco.
Per le funzioni ad 1 input e 1 output numerici, si possono considerare i relativi grafici. Anzi, spesso, come abbiamo visto anche nelle voci precedenti, si possono presentare le funzioni direttamente in forma grafica.
|
È bene indicare le variabili in vari modi,
come accade nelle vita di tutti i giorni. Solo alla fine della scuola secondaria di 1º grado si potrà, gradualmente, arrivare ad attività di esercizio e di
consolidamento astratto in cui si usano variabili con nomi che prescindono
dai vari contesti applicativi. Ed è bene far sì che gli alunni si rendano conto, subito, che una
formula può essere trasformata esprimendo una variabile in funzione di altre
in modi diversi, a seconda delle esigenze, ricorrendo, informalmente, all'idea di funzione inversa, come strumento per trasformare formule.
Questo, del resto, lo devono aver già visto, operativamente, per ricondurre un problema di sottrazione ad un problema di addizione (per trovare quanto fa 100−80
posso trovare quanto devo aggiungere ad 80 per arrivare a 100), o un problema di divisione ad uno di moltiplicazione (per trovare quanto fa 100/20 posso
trovare per quanto devo moltiplicare 20 al fine di ottenere 100). Qualche altro esempio:
| ||||||||||
[Esempi. (a) è il 13; fra quanti giorni è il 29? (b) è il 29, sono trascorsi 13 giorni da quando è partita; quando è partita? (c) avevo 6 euro, me ne sono rimasti 4; quanto ho speso? (d) ho speso 1.50 euro e me ne sono rimasti 13.50; quanto avevo? (e) siamo in 6, dobbiamo formare 15 euro; quanto deve mettere ciascuno se contribuiamo allo stesso modo? ]
Altri esempi li abbiamo visti alle voci "numero", "rapporto e proporzionalità", "formule, termini, grafi".
Una riflessione sull'impostazione dell'insegnamento geometrico nella scuola primaria è bene che sia affrontata a partire da qualche considerazione generale sull'insegnamento geometrico, che possiamo affidare a questa "digressione", fantastica ma molto concreta, sul concetto di angolo. In essa poniamo il problema di come differenziare, per formalizzazione e sviluppo "tecnico", l'insegnamento dei vari temi nei diversi livelli scolastici. Si è preso come riferimento "simbolico" un tema geometrico perché proprio quest'area della matematica è quella che nell'insegnamento viene affrontata in modo più "dissociato" rispetto allo stato attuale della disciplina.
Le moltissime immagini presenti nei commenti relative a tutte le altre voci evidenziano come
anche quest'area della matematica sia intrecciata con le rimanenti.
Gli aspetti di questa interconnessione sono essenzialmente due: da una parte per rappresentare e studiare gli oggetti geometrici
entrano in gioco misure di distanze, angoli, estensioni, spostamenti, … e realizzazione o studio di trasformazioni geometriche
che chiamano in causa numeri, operazioni aritmetiche, rapporti e più in generale funzioni,
dall'altra per rappresentare gli altri oggetti matematici (dai numeri alle funzioni, fino alla statistica e alla probabilità)
si utilizzano, sin dalle prime esperienze culturali (non solo didattiche), grandezze e concetti geometrici, come abbiamo già messo in luce con molti esempi.
Riferendoci ai sistemi di riferimento, da una parte avremo delle rappresentazioni in cui sono conservate le proporzioni tra le due o le tre dimensioni,
dall'altra avremo delle rappresentazioni in cui le diverse scale sono scelte in base all'ordine di grandezza e alla collocazione sulla linea dei numeri delle
diverse entità rappresentate.
Soffermiamoci sul primo aspetto.
Nell'arco della scuola primaria gli alunni devono acquisire (attraverso esperienze, osservazioni, disegni, visualizzazione di immagini ottenute con una fotocamera, …) la capacità di associare visioni a punti di vista:
|
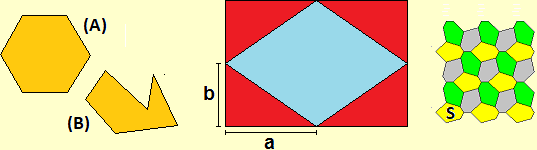
Devono acquisire un po' di lessico, in modo corretto (nella figura sotto a sinistra (A) e (B) sono due esagoni perché hanno 6 lati ovvero 6 angoli - non 6 "angoli interni": non ha alcun senso parlare a scuola di angoli interni; quali sono gli angoli "esterni"?), e imparare a maneggiare figure e calcolare aree di figure semplici senza imparare a memoria formule o ricette (quanto è ampia la parte di stoffa azzurra della bandiera sottostante? quanto è ampia la piastrellatura sotto a sinsitra? - vedi qui):
 |
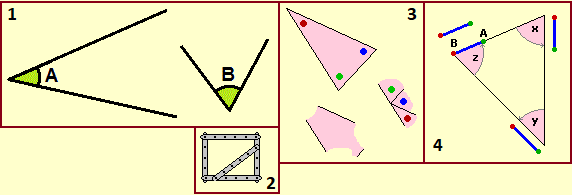
Devono comprendere che cos'è un angolo (inteso come rotazione con cui passare da un lato all'altro, non come "parte di piano" compresa tra i due lati, modo in cui spesso lo presentano i libri, foriero del misconcetto per cui, nella figura 1, l'angolo A è maggiore dell'angolo B), che i quadrangoli non sono rigidi come i triangoli (vedi la figura 2), che tagliando gli "angoli" di un triangolo e riunendoli si ottiene un angolo di 180º (figura 3) e che si può "dimostrare" che questo fatto vale in generale in quanto (figura 4) facendo muovere un bastoncino lungo i lati fino a tornare nella posizione iniziale esso ruota di mezzo giro (vedi qui):
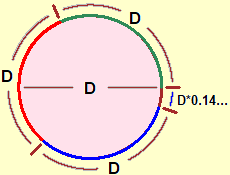 | Si può osservare che quanto detto sopra per le trasformazioni proporzionali dei rettangoli vale anche per i cerchi. Se ingrandisco o rimpicciolisco un cerchio il rapporto tra la sua larghezza, cioè il suo diametro, e la sua lunghezza, cioè il suo perimetro (che nel caso dei cerchi si chiama circonferenza), non cambia, e si vede (come si può osservare misurando la circonferenza di una ruota di biclicletta con un metro da sarta) che è 3 e qualcosa. A questo punto si può dire che esso vale con più precisone 3.141592653… e che viene indicato con la lettera greca π (pi greca), che è l'iniziale della parola greca perimetros: il perimetro del cerchio di diametro D è π·D. |
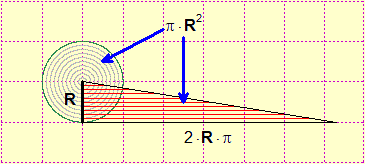
| E si può osservare che un cerchio di raggio R può essere srotolato (come si vede in questa animazione) in un triangolo rettangolo con un cateto lungo quanto la circonferenza e l'altro lungo quanto il raggio, e concludere che la sua area è π·R²: |
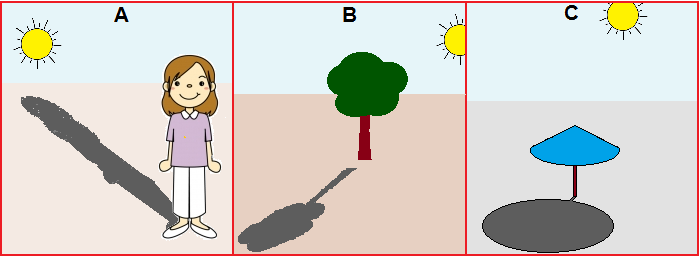
Le attività di disegno a mano libera (e quelle di disegno di case, vie, giardini, … di cui vengono tracciati i contorni su fogli trasparenti appesi alle finestre della classe, quelle di riproduzione fotografica, …) sono occasioni importanti per l'educazione spaziale, intrecciata in modo significativi ad altri aspetti educativi. Un aspetto importante è anche la raffigurazione delle ombre, da affrontare prima liberamente nel contesto di disegni inventati dagli alunni e poi con riflessioni legate ad osservazioni dirette di ombre generate dal sole o da una lampada, a cui far seguire attività di verifica (o di spunto per nuove esperienze) come quella di spiegare a parole quale o quali delle tre figure A, B e C sottostanti sono sbagliate e perché:
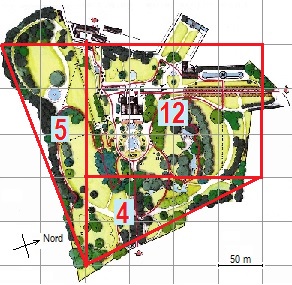
Devono affrontare calcoli di "aree" di piccole estensioni territoriali usando le rappresentazioni cartografiche (l'area del parco sotto a sinistra, visitato dagli alunni, è di circa 12+5+4 quadrati di lato 50 m, cioè …), calcolare "lunghezze" di percorsi contando i passi e poi leggendo le cartine (qual è la strada più breve per andare dall'uno all'altro dei due punti segnati sulla cartina), ruotare di 90º o 180º o ribaltare figure sulla carta quadrettata (come la mezza foglia nella figura sottostante), registrare (dopo attività di disegno come quelle descritte sopra) l'ombra di un bastone verticale al passare del tempo per capire come cambia la posizione del sole, o descrivere (in modo da farsi comprendere) il funzionamento di un tapis roulant osservato in un'azienda visitata:
 |
|
|||
|
Devono imparare che se ho una pila di carte il volume da essa occupato non cambia se la inclino o la ruoto, ma che se ho una scatola come quella sotto a destra (costituita da barre di metallo incernierate e rivestita con tessuto elasticizzato), inclinandola il volume cambia (fino ad annullarsi se abbasso del tutto le facce laterali):
|
Sono acquisizioni concettuali e operative importanti, su cui si tornerà nella scuola secondaria, con
approfondimenti e formalizzazioni ulteriori, e incominciando a staccarsi dai "contesti".
Rinviamo alle considerazioni sul concetto di "spazio" nella parte dedicata alla scuola secondaria di 1º grado per approfondimenti
al riguardo; in esse sono messi a fuoco gli obiettivi di tale livello scolastico e sono approfonditi ulteriormente quelli della scuola
primaria, a cui dovrebbero raccordarsi.
Ricordiamo, solamente, che vanno evidenziati i conflitti tra terminologia matematica e linguaggio comune (i diversi significati di angolo, direzione, distanza,
curva, ...). E va messo a fuoco il fatto che nella pratica possiamo ottenere solo valutazioni approssimate delle aree (e dei volumi).
Come già detto, i concetti dovranno essere ripresi e approfonditi successivamente, nell'ottica di una ripresa a "spirale"
degli argomenti: come sottolineano anche i programmi scolastici da moltissimi anni, non si tratta di fare degli "anticipi", ma di
utilizzare, in modi opportuni, terminologie e concetti che trovano naturali intrecci con altri concetti e di
porre le basi per la costruzione di successivi livelli di formalizzazione. Ci pare fondamentale questo aspetto,
sia per dare una immagine corretta e "viva" della matematica, sia per non favorire irrigidimenti mentali che identificano
i concetti con particolari definizioni, particolari procedimenti di calcolo, … e li classificano in aree (la geometria,
l'aritmetica, …) non comunicanti tra loro.
QUI si possono trovare vari esercizi che esemplificano le considerazioni svolte in questo paragrafo.
Affrontando la statistica descrittiva dovrebbero essere già
stati introdotti i concetti e le tecniche di base per la rappresentazione e lo studio delle variabili casuali.
Affrontando il calcolo delle probabilità si effettua il passaggio al caso in cui si fanno delle "previsioni",
sulla base di considerazioni statistiche, di convinzioni o di informazioni di vario genere.
Al livello della scuola primaria non di devono affrontare problemi complessi ma si deve, comunque, mettere a fuoco,
facendo riferimento a semplici situazioni, il concetto di "probabile", che è presente nelle comunicazioni e nei messaggi verbali
con cui i bambini hanno a che fare sin dai primi anni di vita.
Facciamo solo quattro esempi, riferiti a contesti astratti rispetto alle molte situazioni che si possono presentare in una classe
scolastica:
|
• Abbiamo l'istogramma dei pesi di 27 bambini di 7 anni (quelli che pesano 21 kg e rotti, quelli che pesano 22 kg e rotti, …, quelli che pesano 31 kg e rotti). Se estraggo del tutto a caso un bambino da questo gruppo è più probabile che pesi meno di 26 kg o che pesi almeno 26 kg? (per rispondere basta contare i quadretti che corrispondono ai due casi).
• Lanciamo un dado costruito col cartoncino e ci poniamo solo il problema di quale faccia è più probabile che esca. Facendo poche prove non si riesce a capire, ma facendone molte altre si vede che l'uscita più frequente tende ad essere quella della faccia a cui non vengono incollate linguette.
• Si sta per disputare la partita Milan-Inter. Per Luigi 60 su 100 vince il Milan. Qual è, per Luigi, la probabilità che non vinca?
• Ad una gara di nuoto partecipano 3 ragazzi, A, B e C. In base ai risultati ottenuti in allineamento si ritiene che A e C abbiano probabilità di vittoria doppia di B. Quali sono le loro rispettive probabilità di vittoria? (è facile rispondere - 40%, 20%, 40% - rappresentando
la situazione su carta quadrettata:
Il tema della probabilità viene spesso affrontato in modi "dannosi": si pensi ai molti libri dei livelli scolastici successivi in cui si "definisce" la probabilità come rapporto casi favorevoli/casi possibili, dimostrando l'ignoranza dei più elementari concetti matematici, e favorendo, nei ragazzi, lo sviluppo di misconcezioni che poi sarà difficile smontare. Il tema della probabilità, pur coinvolgendo, in prima battuta, concetti matematici molto elementari (gli stessi della statistica), è difficile da affrontare perché richiede una comprensione profonda delle situazioni da matematizzare, non una banale applicazione di qualche formuletta. Per questo motivo è bene affrontare la messa a fuoco del concetto di "più probabile" facendolo precedere da riflessioni statistiche e considerando situazioni varie, anche non affrontabili con lo schema "casi/casi" accennato sopra, come quelle viste negli esempi precedenti.
Il fatto che gli strumenti probabilistici (e quelli statistici) siano da utilizzare (e i cui esiti siano da interpretare) in contesti non puramente matematici è forse il motivo per cui essi sono spesso trascurati dai docenti o sviluppati in modi del tutto scorretti. È invece essenziale, dal punto di vista educativo, affrontare questa tematica, cercando anche di mettere in luce le difficoltà e gli errori che gli alunni possono commettere affrontando questioni probabilistiche. Questo è un aspetto decisivo per quest'area della matematica, anche per favorire lo sviluppo di attenzioni verso le sciocchezze che i mass media vari spesso propongono facendo riferimento a valutazioni probabilistiche.
Nel secondo biennio della scuola secondaria di 2º grado le aree della statistica e della probabilità troveranno un più forte intreccio quando verranno messi a fuoco gli argomenti teorici per cui, in un esperimento statistico, all'aumentare delle prove il rapporto tra numero delle uscite favorevoli e totale delle uscite tenda a stabilizzarsi sulla probabilità.
Rapporti con le altre aree disciplinari
Nel paragrafo inziale, sul concetto di modello, abbiamo discusso a lungo dei rapporti
tra la realtà e i vari modelli, disciplinari e non, con cui essa, o suoi aspetti particolari, possono essere rappresentati e studiati.
Abbiamo messo in luce anche le differenze tra i modelli matematici e gli altri modelli disciplinari, e le attenzioni didattiche che tutti questi aspetti
devono sollecitare in chi ha il compito di educare le nuove generazioni, soprattutto nelle prime fasce scolastiche.
Mentre le altre discipline si riferiscono a diversi tipi di fenomeni, la matematica è caratterizzata dal tipo di artefatti
che impiega ed è organizzata sulla base della loro proprietà e dei rapporti formali tra essi, anche se alcuni settori di confine (l'informatica, l'econometria,
la fisica matematica, …) sono caratterizzati dalla relazione con certe discipline e aree teconologiche.
Ma, come abbiamo evidenziato sopra, la nascita e lo sviluppo storico dei vari
concetti matematici si è intrecciato agli altri saperi, e la capacità di utilizzare gli artefatti matematici dipende dalle
conoscenze dei contesti in cui essi vengono impiegati. Nel lungo percorso di apprendimenti scolastici ed extrascolatici attraverso il quale si diventa
adulti, cose inizialmente acquisite come astrazioni diventano poi degli "oggetti" concreti per descrivere "realtà" su cui realizzare nuove astrazioni.
Ma, affinché questo processo si sviluppi in modo efficace, occorre che questo passaggio concreto-astratto sia graduale, sia "percepito" dagli alunni,
faccia riferimento ai vari aspetti conoscitivi con cui nella vita di tutti i giorni essi hanno a che fare, per arrivare progressivamente a forme
di sapere organizzate disciplinarmente.