modello
e realtà
Su alcuni concetti / temi matematici da affrontare nei primi anni delle superiori
("intrecciati" all'interno di unità didattiche)
[scuola primaria - A primaria - B sec. 1º: grado sec. 2º: grado - A sec. 2º: grado - B]
Il concetto di modello
Il concetto di numero reale
Altre basi di numerazione
La notazione esponenziale
Le potenze
Le operazioni aritmetiche
I concetti di rapporto e proporzionalità
I diagrammi
Le approssimazioni
Calcolatrici. Calcolatore. Logica
La statistica descrittiva
Variazione e pendenza
Formule, termini, grafi
I concetti di funzione e di risoluzione di un'equazione
Lo spazio
Funzioni circolari
Inversa proporzionalità
Continuità
Sistemi di equazioni. Disequazioni
Funzioni polinomiali
Funzione esponenziale
Strutture matematiche
Calcolo combinatorio
Calcolo delle probabilità
Diversificazioni didattiche
Sono ripresi, con un taglio diverso, più o meno gli stessi contenuti presenti nel documento relativo al livello scolastico precedente.
Le indicazioni sono relative a quanto mediamente si dovrebbe affrontare nella scuola secondaria di 2º: grado.
Esse sono presentate articolate per aree tematiche ma, come via via chiarito, nei percorsi didattici i diversi concetti matematici devono
intrecciarsi tra di loro e con le altre discipline.
Nell'ultimo paragrafo sono presenti indicazioni sulle possibili diversificazioni dello sviluppo didattico nei vari tipi di scuole.
La matematica può essere definita la scienza dei modelli. Il concetto di modello deve dunque avere un ruolo centrale nel suo insegnamento sin dai primi livelli.
Il tema della modellizzazione, per altro, accomuna tutte le discipline (esempi riferiti alla educazione linguistica, alla storia, alla fisica, … sono presenti QUI), anche la filosofia (si pensi, per fare alcuni dei moltissimi esempi, alle analogie/differenze col concetto di modello delle "idee" di Platone, Kant, …, alle interpretazioni dei fenomeni naturali, da quelle dei primi filosofi naturali a quelle di Galileo, alle riflessioni epistemologiche e gnoseologiche). Questo offre numerose e feconde occasioni di interazioni tra l'insegnamento della matematica e quello delle altre discipline.
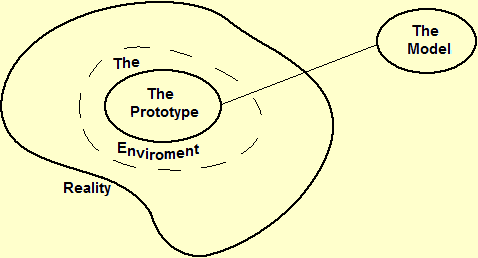
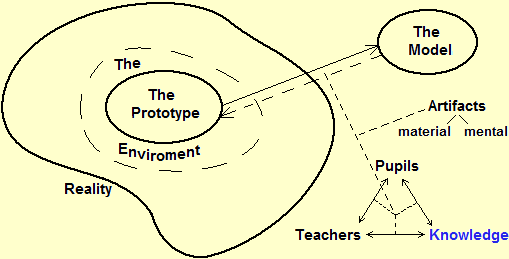
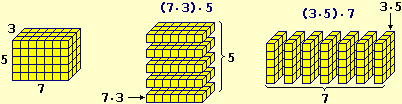
La figura seguente illustra il rapporto tra "modello" e "realtà". Data una situazione reale un modello ne è una rappresentazione semplificata che ne illustra alcuni aspetti, per certe finalità. A seconda delle finalità vi possono essere modelli differenti della stessa situazione (un modello di un aeroplano può avere la stessa forma e colore di un aereo vero ma non volare, o può non assomigliare ad un aereo vero ma volare). La "bontà" di un modello dipende dalla sua adeguatezza agli obiettivi per cui è stato costruito (per evidenziare meglio alcuni aspetti, per generalizzare alcune proprietà, per facilitare il confronto con altre situazioni modellizzate in modo analogo, …). La fase preliminare della modellizzazione circoscrive gli aspetti della realtà coinvolti nel problema che si vuole studiare. Usando la terminologia messa a punto da Aris (Aris R., Mathematical Modelling Techniques, Pitman, London, 1978) e ripresa da Gilchrist (Gilchrist W., Statistical Modelling, John Wiley & Sons, New York, 1984), possiamo chiamare ambiente del prototipo la parte di realtà che viene isolata, non dettagliatamente, in questo modo, e chiamare prototipo gli aspetti del fenomeno o della situazione da modellizzare (incluse le assunzioni, le intuizioni, le percezioni, le intenzioni, … di chi costruisce il modello) di cui si vorrà tener conto nella rappresentazione. Tutto questo può essere schematizzato nel modo seguente:
| modello e realtà |
 |
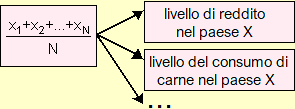
Lo stesso modello può essere impiegato per rappresentare situazioni diverse. Un esempio molto semplice è il concetto di media aritmetica, che può essere usato per indicare, in un dato paese, il consumo pro-capite di carne, il reddito medio per famiglia, l'altezza media dei ventenni, … Un altro esempio comune è la diretta proporzionalità, che può essere impiegata per rappresentare la relazione che intercorre tra il peso di un prodotto alimentare e il suo costo, tra l'allungamento di una molla e il peso dell'oggetto ad esso appeso, tra le distanze tra le parti di un'automobile e quelle tra le parti corrispondenti in un suo modellino, …
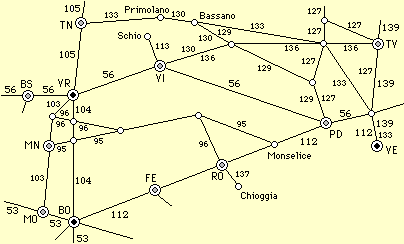
E una stessa situazione, a seconda delle esigenze, può essere rappresentata con modelli diversi. La figura sottostante a destra riproduce parte dell'indice grafico stampato nella prima pagine di un orario ferroviario: è una cartina in cui sono riprodotte le linee ferroviarie e sono indicati i relativi quadri dell'orario; essa è un modello diverso da una usuale cartina geografica in quanto non rappresenta correttamente le distanze e le direzioni.
 |  |
Vediamo un altro esempio, semplice, in cui affrontiamo un problema con due modellizzazioni matematiche differenti. Voglio studiare il legame tra la distanza DS lungo la strada e quella DA in linea d'aria di Genova dalle altre località dell'Italia Settentrionale. Posso affrontare il problema in modo concettuale (capire che quando DA = 0 ho DS = 0, che DS ≥ DA, che data la presenza di molte curve il rapporto tra DS e DA sarà circa pari al rapporto tra semicirconferenza e diametro, ossia circa 1.5, …). Oppure posso studiare il problema in modo empirico (raccogliere i dati relativi alle minime distanze stradali da Genova dei capoluoghi di provincia di Piemonte, Lombardia e Veneto, e, in modo approssimato, usando correttamente le cartine o altre fonti, quelli relativi alle distanze in linea d'aria, rappresentarli graficamente, cercare di approssimare i punti con una retta, mettere a punto il modo in cui realizzare e interpretare questa approssimazione, …). Questo secondo approccio è illustrato a lato (anche con questo approccio stabilisco che la relazione è circa DS = 1.5·DA; posso poi studiare con tecniche statistiche che precisione assegnare ad 1.5). | 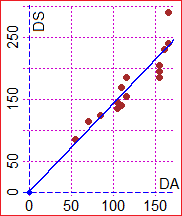 |
Semplificando, possiamo dire che il prototipo era la relazione tra le distanze in linea d'aria di Genova dai capoluoghi di provincia dell'Italia Settentrionale e le minime distanze lungo la strada, mentre l'ambiente del prototipo era riferito genericamente alle distanze di Genova dalle varie località. Il problema lo abbiamo modellizzato con l'equazione DS = 1.5·DA.
In molte situazioni occorre poi reinterpretare il modello verificandone l'adeguatezza a
rappresentare il fenomeno studiato ed eventualmente ridefinire il prototipo stesso. Possiamo raffigurare
meglio la situazione modificando lo schema precedente aggiungendo una freccia
Questa figura prende in esame non solo i rapporti modelli-realtà ma anche gli "strumenti" impiegati per costruire i modelli e come la loro messa a punto interagisca col processo educativo, ossia con gli alunni, i docenti e il complesso delle conoscenze (le discipline, le tecniche, …).
I modelli sono rappresentazioni astratte di oggetti o fenomeni "reali" (di tipo materiale: una rappresentazione topografica è il modello di un territorio; di tipo sociale: i concetti di "verbo", "sostantivo", ... sono dei modelli per rappresentare certi elementi della comunicazione verbale; … o di tipo astratto: la "proprietà commutativa" è un modello per descrivere un aspetto di alcune operazioni matematiche).
I modelli sono costruiti utilizzando artefatti cognitivi, ossia "oggetti materiali" (carta, segni, suoni, colori, …) o "costruzioni artificiali" ad hoc (il linguaggio, i concetti, …) che l'uomo usa come protesi della sua mente. Il termine "cognitive artifact" fu introdotto da Donald Norman nel 1993 (Norman D.A., Things that Make us Smart, Wesley Publishing Company, Addison, 1993), mentre quello di "prosthesis tools" fu proposto da Jerome Bruner nel 1986 (Bruner J.S., Actual Minds, Possible Worlds, Cambridge, Mass., Harvard University Press, 1986).
La messa a punto degli artefatti cognitivi per modellizzare le situazioni non avviene episodicamente, ma in un contesto sociale di crescita culturale che viene via via ad organizzarsi in forme strutturate di conoscenza, che vengono trasmesse da una generazione all'altra attraverso processi educativi, in cui gli alunni e i docenti interagiscono tra loro e col sapere, quello in costruzione e quello consolidato. Queste reciproche interazioni sono descritte dal triangolo didattico sopra raffigurato che (al di là delle sue riproposizioni fatte contemporaneamente, all'inizio degli anni '80, da vari ricercatori in didattica: Herbart, Chevallard, …) risale a Cicerone (De Oratore, 55 a.C.). Esso fu poi usato anche da Quintiliano (Institutio Oratoria, 96 d.C.), e, successivamente, da molti altri. L'idea di Cicerone, a sua volta, era una rielaborazione di un analogo "triangolo", ai cui vertici c'erano il simbolo (o segno), la referenza (o significato del segno) e il referente (o oggetto a cui si riferisce il segno), messo a punto da Aristotele (La Retorica, IV sec. a.C.) per illustrare la "retorica".
Quanto osservato sin qui vale per tutte le discipline e le forme organizzate di sapere. Ma la matematica ha la specificità di non essere caratterizzata da una particolare area di problemi o di fenomeni che cerca di modellizzare (come la fisica, la storia, la linguistica, …), bensì dalla tipologia degli artefatti che impiega per la costruzione dei modelli, e che vengono utilizzati in tutte le altre discipline. Quindi lo schema grafico visto sopra (che di per sé è una semplificazione) al fine di rappresentare la situazione dell'insegnamento della matematica deve essere almeno arricchito col tratteggio verticale raffigurato a lato: gli artefatti, per la matematica, presto, da strumenti conoscitivi diventano degli oggetti di conoscenza, da modelli che "astraggono" a partire da situazioni diventano man mano degli strumenti "concreti" per mettere a punto nuove astrazioni, in una spirale senza fine. Il sapere matematico, che nasce dai contesti modellizzati, si organizza internamente non sulla base di questi, ma dei rapporti e delle analogie strutturali tra i suoi artefatti. | 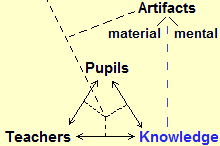 |
La situazione, poi, si fa più complessa in quanto sia il "triangolo", sia la tipologia degli "artefatti", con l'avvento dell'informatica, sono divenute più articolate: il software è diventato un interlocutore "animato" che interagisce tra i diversi soggetti, in modi molto diversi a seconda dell'uso che ne viene fatto e della consapevolezza con cui viene impiegato. Senza complicare ulteriormente la schematizzazione precedente, occorre tener presente che il software ha ora, e avrà sempre più, una incidenza decisiva nel modo in cui i diversi aspetti interagiscono tra di loro.
[Sono spesso usate espressioni particolari per individuare specifici artefatti cognitivi. Si tratta di espressioni usate in modi diversi dai vari autori, anche all'interno della stessa disciplina. Ne richiamiamo alcune, con alcune possibili interpretazioni. Un segno è un artefatto cognitivo costituito da un "oggetto" che (per una particolare comunità di persone) rappresenta un particolare significato o può essere una parte ben individuabile di tale oggetto (può essere un segno ad esempio il due punti, ":", ma possono esserlo anche ciascuno dei due punti che lo formano). Un simbolo è un oggetto, un individuo o un'altra cosa più o meno concreta usata per evocare un oggetto reale o un'entità astratta; in "matematica" è un oggetto costruito con particolari segni che rappresenta, in una particolare area della matematica, una costante, una variabile, una funzione, una relazione, …. Un segnale è un'immagine, una frase, un suono o un'azione che serve per comunicare un messaggio, un ordine, …]
Riassumendo, possiamo comunque dire che lo studio della matematica si articola nel rapporto (non lineare) tra porsi problemi, modellizzare le situazioni per affrontare la soluzione dei problemi, costruire e ricorrere a teorie che organizzano internamente i rapporti tra gli artefatti impiegati per la costruzione dei modelli e mettono a punto nuovi eventuali artefatti.
Tutto ciò rende cruciale, nell'educazione matematica, il ruolo dell'insegnante. Egli deve:
• progettare e curare percorsi didattici che diano concretezza ad artefatti man mano più lontani da forme elementari di percezione,
• far emergere i conflitti realtà-concetti astratti
(da quelli tra specchi "fisici" e "matematici" ai molti
altri presenti sin dalle prime esperienze di insegnamento)
che, se non esplicitati, rischiano di essere fonti di misconcezioni,
mentre, se affrontati, sono un'occasione per trasformare una "opposizione distruttiva" in una "dialettica produttiva", che contribuisca a costruire
un'immagine adeguata della matematica come disciplina,
• educare alla scelta dei modelli (non esiste "il" modello migliore) a seconda delle esigenze e delle "risorse" (artefatti fisici e concettuali) disponibili,
• organizzare l'insegnamento in modo che i riferimenti ad oggetti o situazioni reali non siano solo dei pretesti ma instaurino
dei rapporti virtuosi con le conoscenze (e le motivazioni) extra-scolastiche degli alunni, decentrando, cercando di aver come riferimento
non solo le proprie conoscenze e le proprie motivazioni ma, in un rapporto dialettico, anche quelle degli alunni,
• e dare organicità alle conoscenze da loro man mano acquisite in campo matematico
(anche affiancando allo studio di situazioni problematiche la messa a punto - a partire da esse - di nuovi concetti e
il consolidamento di alcune abilità operative attraverso opportuni esercizi,
che dipendono dal livello delle conoscenze e delle tecnologie storicamente disponibili)
in modo che diventino un solido terreno di partenza per nuove astrazioni,
• tenendo conto che, specie nei primi livelli di istruzione, la costruzione di rapporti virtuosi con l'extra-scuola
dipende anche dal coinvolgimento delle "famiglie": occorre farle partecipare "culturalmente" al progetto educativo che si sta portando avanti
(partecipare "culturalmente" non vuol dire "fare i ripetitori", ma collaborare con i docenti nella costruzione di rapporti tra le attività
scolastiche e la vita extrascolastica); questo è uno dei compiti più difficili; anche questo aspetto andrebbe opportunamente inserito
nel "triangolo didattico" considerato sopra …
È solo dopo l'avvio della costruzione del significato della matematica come scienza dei modelli che l'insegnante può gradualmente costruire il significato delle definzioni e delle dimostrazioni in ambito matematico, mettendo a fuoco le differenze dagli altri significati che nel linguaggio comune hanno sia le definizioni (in un dizionario esse si basano su una banca di parole - the defining vocabulary - di cui non viene spiegato il significato) che le dimostrazioni (la dimostrazione della colpevolezza di un imputato è al di là di ogni "ragionevole" dubbio, non è "certa"). Ritorneremo in molti altri punti sia sulle definizioni: QUI, QUI, QUI, QUI, QUI, QUI, che sulle dimostrazioni: QUI, QUI, QUI, QUI, QUI, QUI.
QUI trovi vari link a "i limiti dei modelli" che illustrano come l'individuazione di una relazione matematica
(statistica, funzionale, …) tra due grandezze reali non indichi sempre la presenza di una relazione
di causa-effetto tra di esse. A questo aspetto, implicitamente già presente tra i punti precedenti, è
assai importante dare rilievo nell'insegnamento.
La padronanza della rappresentazione decimale dei numeri dovrebbe essere uno degli obiettivi dell'insegnamento nella scuola media inferiore. È essenziale, all'inizio delle superiori,
impostare delle attività didattiche che consentano di verificare questa padronanza ed
eventualmente avviare delle attività che consentano di consolidarla.
In particolare l'interpretazione dei numeri come posizioni sulla retta graduata
deve diventare naturale e immediata da parte degli alunni: è uno tra i pochi automatismi (di elaborazione, associazione, passaggio da una rappresentazione a un'altra, ...) che tutti devono saper esercitare senza sforzi mnemonici o riflessivi (per liberare risorse mentali da dedicare ad aspetti più concettuali): sono abilità/atteggiamenti che è opportuno consolidare/mantenere allenati continuamente.
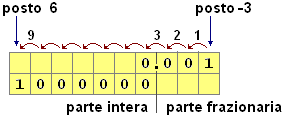
Fondamentale è anche consolidare il significato del posto di una cifra e mettere bene in luce come
la "posizione di riferimento" per la lettura di un numero non sia il punto (la virgola) decimale, ma la "cifra di posto 0":
probabilmente questa confusione è all'origine
delle difficoltà nella lettura/interpretazione dei numeri con cifre frazionarie che manifestano alcuni alunni.

Osserviamo, infine, che spesso si ha a che fare con numeri che rappresentano misure; occorre prestare attenzione ai misconcetti che si possono creare rappresentando questi valori mediante variabili. Un esempio: se uso s per indicare la posizione in chilometri lungo la strada in cui mi trovo dopo t minuti, se dopo t0 minuti mi trovo a 37 km dall'inizio della strada e se v è la velocità costante in chilometri all'ora a cui sto viaggiando, posso scrivere s = v·(t−t0)/60+37; ma devo stare attento ad usare sempre le stesse unità. Se usassi le variabili per rappresentare le grandezze, non le loro misure in opportune unità, dovrei scrivere: s = v·(t−t0)+37 km.
È opportuno, nelle prime lezioni all'inizio delle superiori, organizzare attività didattiche che consentano di • esplorare e rivedere, assieme ad altre, abilità di base che dovrebbero essere padroneggiate alla fine della media inferiore e, contemporaneamente, • introdurre nuovi metodi, argomenti e riflessioni che permettono di coinvolgere e motivare anche alunni che quelle abilità già padroneggiano (senza isolare, quindi, il "recupero" dai nuovi apprendimenti).
È opportuno anche far riflettere gli alunni sulle ambiguità con cui, nel linguaggio verbale,
vengono espressi i numeri con "punto", ossia i numeri con "virgola" (per l'importanza di questa attenzione al
confronto con il linguaggio comune vedi QUI i link alla voce "ling. matem. e lin. comune"),
oltre a far notare (ad es. osservando il
menu-opzioni di un computer o di un cellulare) le diverse
convenzioni ("," e ".") che, in ambito commerciale e nella vita quotidiana, si usano da una parte in Italia, dall'altra
nei Paesi Anglosassoni e nel mondo scientifico, per separare la parte intera da quella frazionaria.
Intrecciate alla revisione e al consolidamento del concetto di "numero" sono le riflessioni sugli ordine di grandezza, sul
calcolo mentale approssimato, sulla linea dei numeri (e sui numeri negativi), …:
vedi i successivi commenti fino al paragrafo "la statistica descrittiva" escluso.

La padronanza dei numeri decimali limitati, la capacità di utilizzare strumenti di misura graduati, … sono fondamentali, in particolare, per avviare una sistemazione del concetto di numero reale, che inzialmente potrà essere chiamato semplicemente "numero" (o numero illimitato), rinviando l'aggiunta dell'attributo reale a quando servirà per distinguerlo dai numeri complessi. Non è certamente un concetto difficile: già i babilonesi (circa 2 millenni a.C.) padroneggiavano un sistema di scrittura posizionale, anche se con base sessanta (vedi QUI): ad es. 1 24 51 10 (scritto usando simboli diversi per le cifre) rappresentava il numero 1+24/60+51/60²+10/60³; sapevano calcolare la radice quadrata di un numero con qualunque precisione (avevano l'idea che si poteva andare avanti e che fermandosi ad un certo punto si otteneva una approssimazione, di cui sapevano valutare l'errore); … I libri di testo della scuola italiana (quelli più diffusi) sono tornati indietro di vari millenni, e con grossolani errori (vedi più avanti).
Per una corretta e significativa introduzione dei numeri è opportuno scegliere un
approccio costruttivista; in breve:
– numeri reali come opportune successioni di caratteri
(cifre, "." e "–"), con una opportuna
relazione di "eguaglianza" (3.7999…=3.8000…,
ecc.),
– definizione algoritmica delle operazioni sui numeri
decimali limitati,
– estensione di queste ai numeri reali mediante i concetti
di approssimazione e, senza formalizzazioni, di limite/funzione
continua (es.: per ottenere il risultato di x·y con una certa
precisione basta operare su intervalli di indeterminazione per x e
per y sufficientemente piccoli).
I numeri naturali, interi, periodici, decimali
limitati e limitati in altre basi vengono studiati come particolari
sottoinsiemi di R chiusi rispetto ad alcune operazioni.
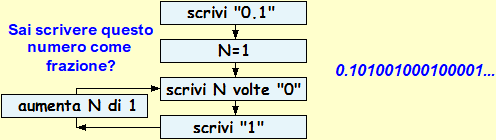
Gli alunni hanno già incontrato numeri decimali illimitati nei primi livelli scolatici, come √2, π, 0.333…, 3.7999… (= 3.8000…).
Hanno già osservato che alcuni numeri, come gli ultimi due precedenti o come quello rappresentato nella figura soprastante (0.101001…), possono essere descritti esattamente,
cifra dopo cifra, con un semplice algoritmo, ed hanno scoperto che alcuni, come solo i primi due precedenti, posso essere espressi come risultato
della divisione tra due interi. A questo punto si può mettere a fuoco che questo accade per tutti i numeri periodici (a cui occorre mettere a fuoco
che appartengono anche i numeri interi e decimali limitati), e si possono introdurre le parole razionali e irrazionali per distinguere i numeri
che possono essere espressi come frazione tra due numeri interi e gli altri (che sono la stragrande maggioranza).
E occorre sottolineare che l'impiego di questi aggettivi ("razionale" e "irrazionale")
in questo contesto non ha niente a che fare con il loro uso nella lingua comune (nei signficati di "ragionevole" e "privo di ogni logica") ma deriva dall'uso
della parola latina "ratio" per indicare il rapporto tra numeri: in un numero irrazionale non è detto che le cifre si susseguano in modo caotico.
Non è opportuno, ovviamente,
introdurre i numeri reali per via assiomatica, né presentare
la costruzione dei vari insiemi numerici a partire da N:
– sarebbe dispendioso e difficile introdurre gli strumenti
algebrico-logico-insiemistici per effettuare "correttamente"
la costruzione (anche il solo passaggio) agli interi
– e, soprattutto, a questo livello, non se ne vedono
motivazioni "didattiche" (in un corso universitario di algebra la
costruzione di Q a partire da N può essere invece
un'occasione di applicazione di concetti come partizione, immersione,
…) o "culturali" (in un corso universitario sui fondamenti della
matematica può essere invece significativo costruire con
tecniche insiemistiche a partire dall'aritmetica di Peano un modello
per gli assiomi dei numeri reali).
L'introduzione dei numeri deve poi intrecciarsi ad
argomenti di statistica, a riflessioni sull'uso dei mezzi
di calcolo, sui codici, …
Nei libri di testo più diffusi si trovano gravi errori didattici e concettuali. Basti pensare all'introduzione dei cosiddetti "numeri assoluti" (accoppiata a radicali assoluti e altre amenità), all'introduzione di "+" davanti ai numeri positivi (tra cui non vengono fatti rientrare i numeri naturali diversi da 0), …, che sono solo frutto di una grossolana incomprensione della natura della matematica e dell'orecchiamento, frainteso, di questioni relative ai fondamenti della matematica (vedi il seguente esercizio).
Il modo in cui introdurre i numeri reali presentato in questo paragrafo,
dal punto di vista "fondazionale",
ha evidenti collegamenti con la "aritmetizzazione" dei numeri reali proposta da Cantor (numeri reali e operazioni
tra essi come "completamento per continuità" della struttura dei numeri razionali), ma invero non
fa altro che presentare il modo in cui, da quando si è diffusa la notazione posizionale,
si scrivono e si opera sui numeri reali (Cantor non si proponeva di introdurre e definire la
struttura dei numeri reali, che era già nota, ma di caratterizzarla, per fini fondazionali, come estensione
di quella dei razionali, e di farlo con un procedimento che, rispetto a quello di Dedekind, fosse più
vicino alla pratica matematica). Per approfondimenti sugli aspetti fondazionali (e le
motivazioni culturali dell'approccio qui presentato), esamina questo documento: I Numeri Reali
Nei libri di testo per le superiori spesso si trova una caricatura dell'approccio di Dedekind:
i numeri reali vengono introdotti come elementi di separazione tra classi contigue di numeri razionali, senza rendersi conto che, se i numeri reali
non li ho già, non esiste alcun elemento di separazione se non nei casi in cui appartenga a una delle due classi, e sia quindi razionale; e senza porsi il problema
che, comunque, si dovrebbe trovare il modo di collegare (e in modo "corretto") questa "costruzione" all'usuale modo di scrivere i numeri.
Per gli errori e le imprecisioni che in genere costellano queste "trattazioni" le si confrontino con la traccia di uno sviluppo "alla Dedekind"
corretto (e affrontabile solo a livello universitario) che può essere trovata nel documento a cui si accede dal precedente link.
Le prime basi non decimali da introdurre e che gli alunni devono padroneggiare sono quelle impiegate nella misura dei tempi (basi 12, 24, 60), sulle quali hanno competenze operative acquisite gradualmente nel corso della loro vita. Compito dell'insegnamento è gestire la transizione da queste competenze alla esplicitazione e formalizzazione dei modi in cui passare da una di queste basi alla base dieci, e viceversa, e su come operare tra numeri espressi in queste basi, non introducendo regole meccaniche abbreviate, ma procedimenti e forme di descrizione che non taglino i collegamenti con i modi di operare nelle vita quotidiana e che non oscurino i riferimenti ai concetti di "rapporto" e di "cambio" di unità di misura.

Consolidate le analogie tra base dieci e base sessanta e i modi in cui passare
dall'una all'altra, il contesto della codifica dei numeri nei dispositivi elettronici (e
quello della riflessione sulle "strane" uscite dei mezzi di calcolo) potrà
costituire, in un secondo tempo, l'occasione e la motivazione per una estensione ad altre basi di numerazione.
Un approccio precoce a una trattazione generale delle basi di rappresentazione dei numeri, specie
se inizialmente riferito a basi di cui non si fa uso nelle esperienze quotidiane,
– è
didatticamente controproducente:
• sono fondamentali la esplicitazione e riflessione sulle competenze operative acquisite esperienzialmente,
• il loro consolidamento attraverso la messa a punto di metodi
che aiutino ad affrontare situazioni non agevoli per il calcolo mentale,
• la individuazione
di analogie tra situazioni diverse e l'utilità di una loro unificazione concettuale,
• l'acquisizione della abitudine/capacità di ricollegarsi ad esemplificazioni e a situazioni prototipo per ricostruire concetti e metodi generali (abitudine/capacità difficilmente acquisibile senza passare attraverso le frasi precedenti),
• …
– e non offre motivazioni culturali né un'immagine adeguata della natura
della matematica.
| È importante introdurre subito l'uso della notazione esponenziale e metterne a fuoco l'utilità, contestualmente al consolidamento dell'uso di unità di misura diverse e della scrittura posizionale e all'educazione all'uso delle calcolatrici tascabili e allo svolgimento mentale dei calcoli approssimati. | |
| Oltre alla comodità della notazione esponenziale per descrivere numeri grandi e piccoli, è bene far emergere il fatto che essa facilita il controllo sintattico e semantico su ciò che si scrive, che usarla per introdurre su una calcolatrice numeri con ordini di grandezza grandi o piccoli rende più difficile commettere errori di battitura (ad es. dimenticare qualche zero), che consente una descrizione non ambigua delle approssimazioni. Quest'ultima osservazione potrà essere sviluppata esplicitamente quando si affronterà uno studio più sistematico dei "numeri". |  |
| Le tematiche "statistiche" offrono molte occasioni per inserire in modo naturale le prime attività e riflessioni sull'uso della notazione esponenziale e (vedi sotto) delle potenze. | |
La padronanza dell'elevamento a potenza è fondamentale nei più
svariati campi della matematica. Deve essere verificata, consolidata e approfondita
a partire dai primi anni di scuola superiore, non attraverso attività
avulse da contesti, ma in relazione a situazioni d'uso in cui le potenze intervengano
in modo significativo e che possano costituire dei solidi punti di riferimento
per la concettualizzazione e la memorizzazione.
Fondamentale, a tal riguardo, è il riferimento alle potenze di 10.
Per altro le attività con le potenze (se non vengono subito ridotte alla applicazione meccanica di regolette) possono aiutare a consolidare il significato dei numeri negativi e delle addizioni con essi. Ad es. questo è possibile se nella spiegazione o nella correzione di errori in calcoli
come quello di
|
Nel riprendere questo concetto, già avviato nelle scuole precedenti, è opportuno fare qualche prima riflessione sulle "definizioni":
nella definizione della potenza ad esponente intero l'esponente indica la quantità di volte
per cui a partire da 1 si effettuano delle moltiplicazioni (o delle divisioni, se l'esponente è
negativo) per la base. Questa definizione, che "traduce", ed estende, la usuale definizione ricorsiva (a0=1, an+1=an·a), è immediatamente collegata al
concetto di ordine di grandezza (esponente della potenza di 10 della notazione scientifica). Corrisponde anche a come si effettua il calcolo con un ciclo "for": a=3; n=7 p=1; for(i in 1:n) p=p*a; p # 2187 a^n # 2187 |
 |
Ricordiamo che in molti libri è diffusa la seguente definizione «an è il risultato di n moltiplicazioni di a per sé stesso», che è ovviamente sbagliata (se si parte da a invece che da 1 le moltiplicazioni per a sono n–1, non n). È facile che (durante la discussione o di fronte a una domanda esplicita) lo stesso errore venga fatto anche da qualche alunno (che abbia già memorizzato questa definizione in precedenti esperienze scolastiche). E` un tipico esempio di definizioni "bla-bla" che gli alunni studiano e ripetono senza capire (il concetto viene capito operativamente, per altri canali).
È opportuno far notare ai ragazzi, quando si indicano una successione di operazioni del tipo
Sull'estensione delle potenze dal caso dell'esponente intero a quelli dell'esponente
frazionario (nel cui ambito deve essere affrontato lo studio dei radicali, che non devono essere studiati come oggetti
indipendenti dalle potenze, con loro regole e proprietà)
e, poi, dell'esponente reale (in particolare, per dare il senso a trattamento di grafici come quello di
Ovviamente nelle attività a cui si è accennato nei punti precedenti occorre richiamare il significato delle 4 operazioni (relazioni tra loro, situazioni di cui sono modello, interpretazione geometrica, …). Queste osservazioni e riflessioni svolte in più occasioni possono essere esplicitamente riprese in modo unitario, per consolidare alcuni concetti e abilità di base, ed anche per creare i presupposti per successivi interventi didatticamente efficaci nei confronti degli alunni che manifesteranno difficoltà nell'impostazione delle equazioni. È utile, in particolare, discutere con gli alunni le loro strategie di calcolo mentale, mettendole in discussione se errate, proponendo alternative, … ma senza porsi l'obiettivo di imporre loro procedimenti diversi da quelli che impiegano, se corretti: persone diverse possono, per i motivi più vari, preferire seguire ragionamenti di tipo differente.
Se è il caso è bene riprendere gli elementi di base delle tecniche delle 4 operazioni, recuperando abilità di calcolo, mentali e non, spesso oscurate da "tecniche veloci" (e "volatili") su cui gli alunni sono stati fatti esercitare nei livelli scolastici precedenti (vedi QUI per avere un'idea di come "dovrebbero" essere state introdotte le tecniche di calcolo nella scuola di base).
Occorre poi tener presente l'eventuale presenza di alunni con disturbi di tipo discalculico.
La discalculia è presente in circa il 2% della popolazione, quindi in una classe di 25 alunni della scuola
di base si ha circa il 50% di probabilità di avere un alunno con alunno con tali problemi; la probabilità di averne due è
molto più bassa, circa il 25%; di averne tre è circa del 10%. Un insegnante di scuola elementare nel corso della sua
carriera dovrebbe incontrare circa 5 alunni con disturbi discalculici (spesso, per incompetenza di chi fa queste diagnosi,
vengono segnalati come casi discalculici situazioni che non rientrano in questo ambito). Un insegnante di scuola media inferiore
ne potrebbe incontrare una decina. Per i docenti di scuola superiore il numero dipende dal tipo di scuola in cui
si insegna.
Che fare in queste situazioni? Innanzi tutto occorre segnalare che la discalculia si manifesta in alunni con intelligenza
normale e senza disturbi di tipo neurologico. Occorre quindi, a partire dalla scuola di base, come con gli altri alunni,
far riferimento a tutte le situazioni della vita reale in cui si usano i numeri, far riferimento ad algoritmi in cui
sia trasparente il significato del procedimento e, in particolare con loro, appoggiarsi subito a sussidi di tipo
tecnologico per lo svolgimento delle attività di calcolo, limitandone inizialmente l'uso da parte degli altri alunni.
Si possono impiegare le usuali calcolatrici o calcolatrici
presenti nel software, come quelle a cui si può accedere da QUI;
si può ricorrere al "traduttore" di Google (vedi QUI)
in cui si possono scrivere numeri e operazioni (come: 7.5 1500 12% 5000000 3/4)
e ascoltare la loro lettura; si può anche (come suggerito dal sito internazionale che si occupa della
discalculia) usare WolframAlpha (vedi QUI,
clicca poi su Elementary Mathematics, Arithmetic). Le difficoltà di tipo discalculico sono
in buona parte legate a problemi di memorizzazione (analoghi per alcuni aspetti a difficoltà simili
che possono subentrare in alcune persone in seguito a incidenti o a piccoli ictus) che non compromettono
la comprensione delle attività matematiche se ci si appoggia - come si può fare ormai da vari decenni -
all'uso del computer. È, ovviamente, opportuno che gli insegnanti stimolino questi alunni, sin dai
primi anni di scuola, ad usare opportunamente i mezzi di calcolo.
Un disturbo per molti versi simile (e leggermente più frequente, circa due volte la discalculia) è la dislessia, ossia la difficoltà nel leggere e a volte scrivere le parole che si manifesta in genere con la trasposizione e l'inversione di gruppi di lettere. L'uso del computer è, evidentemente, di grande aiuto anche per far fronte ai problemi che essa genera. Si può ricorrere,
in modo simile a quanto detto per la discalculia, a Google, ai programmi di scrittura gratuiti (come OpenOffice, LibreOffice, …) e ai loro controllori ortografici (che propongono alternative
a quanto digitato). La stessa battitura dei testi sul computer, e l'osservazione di quanto si sta scrivendo, e la possibilità di correggere quanto scritto, è di per sé
di aiuto per chi ha problemi di questo genere.
Le attività sulla linea dei numeri, in particolare quelle che coinvolgono i numeri negativi,
sono assai utili per consolidare (anche attraverso la riproposizione di esercizi simili)
l'abitudine ad appoggiarsi alla (immagine mentale della) linea dei numeri. È importante introdurre
correttamente i numeri negativi, non far usare regolette (foriere di misconcezioni) come "−" per "−" fa "+",
non far mettere il segno "+" davanti ai numeri positivi, ….
Errori frequenti frutto di queste misconcezioni sono, ad es., quello di trasformare
Sulle prime tracce dell'uso dei numeri negativi da parte dei babilonesi (a cui abbiamo accennato discutendo delle "operazioni aritmetiche") si possono trovare considerazioni in vari libri di Martin Gardner e in molti articoli scientifici, ad esempio vedi QUI.
È utile interpretare gli errori o le difficoltà di calcolo numerico, scritto o mentale, degli alunni, farne esplicitare le origini, far fare verifiche delle proprietà usate erroneamente (o di quelle non usate) su semplici casi, ricorrere a modelli interpretativi di tipo geometrico per generalizzare esempi numerici, come i seguenti (il primo illustra una proprietà utilizzabile, il secondo un errore):
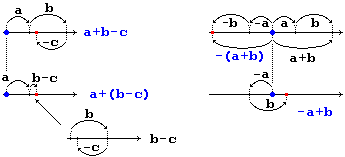
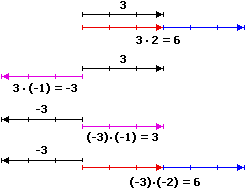 |
Le operazioni con numeri negativi sono facilmente interpretabili, se introdotte interpretando la "negazione" come un'inversione
della direzione. Ad esempio, nel caso della formula |
 |
Queste riflessioni/attività dovrebbero rendere più facile, da parte degli alunni che incontrano difficoltà di fronte a ragionamenti più formalizzati, la comprensione e l'interiorizzazione delle trasformazioni a cui può essere sottoposto un termine numerico. È utile, successivamente, introdurre, in modo operativo, rappresentazioni grafiche della struttura dei termini.
|
|
+
___/ \___
SQR /
| ___/ \___
2 * C
__/ \__
A B |
+
___/ \___
SQR /
| ___/ \___
2 * C
__/ \__
A B |
+
___/ \___
SQR /
| ___/ \___
2 * C
__/ \__
A B | ||
| radice quadrata | moltiplicazione | divisione |
Nota. Le operazioni aritmetiche sono le prime funzioni numeriche con cui si ha a che fare nella vita scolastica. Dopo un primo avvio, in cui si riprende confidenza con le operazioni e in cui si avvia alla formalizzazione delle funzioni, occorre inquadrare le operazioni in questo concetto più generale. Il termine operazione in matematica viene usato in diversi modi nelle varie aree della disciplina. In genere indica una funzione (o applicazione) descritta attraverso un procedimento (in senso lato, non necessariamente "meccanico") e che assume un rilievo particolare nella caratterizzazione di un certo tipo di struttura matematica o di un particolare settore della matematica; il simbolo funzionale utilizzato per descriverla viene chiamato operatore, ma a volte con questo termine si indica la funzione stessa. Esempi: l'unione tra due insiemi (è un'operazione che a due insiemi associa un altro insieme, e che dà una certa struttura algebrica alla classe dei sottoinsiemi di un certo insieme), la composizione di funzioni, il passaggio al limite, la derivazione e l'integrazione, i prodotti scalare e vettoriale, … Vedi QUI per qualche nota ulteriore.
Nello sviluppo dell'insegnamento della matematica nelle sue
varie aree è importante via via mettere in luce (in modo occasionale, senza
soffermarsi troppo) analogie e differenze tra modi in cui si opera sui numeri e modi in cui
si opera su altri oggetti matematici. Queste considerazioni sparse possono costruire gradualmente
il terreno su cui, poi, tra la fine del biennio e l'inizio del triennio, impostare (nelle classi non troppo "difficili") una sistemazione più
organica. Su questi aspetti torneremo più avanti:
vedi formule, termini,grafi e strutture matematiche.
I concetti di rapporto e proporzionalità
Buona parte del primo anno della scuola superiore sarebbe opportuno dedicarla a porre solide basi relativamente alla padronanza dei numeri (in base dieci), al concetto di rapporto, al concetto di funzione, all'uso dei grafici, all'uso di variabili, termini ed equazioni per rappresentare relazioni tra grandezze, alla rappresentazione di algoritmi. Spostare l'attenzione su aspetti secondari o su nuovi concetti che al momento possono essere affrontati solo con presentazioni erronee (come ad esempio accade nelle usuali introduzioni dei polinomi, non riferite ai concetti di funzione e di equazione) o con apprendimenti meccanici e superficiali (il calcolo letterale senza un'adeguata comprensione del significato delle linguaggio letterale e del calcolo simbolico e del ruolo delle modellizzazioni algebriche, il calcolo in basi diverse senza la padronanza dei concetti di rapporto, codifica, …) sarebbe controproducente.
In particolare (all'interno di percorsi didattici in cui sono presenti gli altri concetti sopra richiamati) è opportuno riprendere, consolidare ed estendere la padronanza e la conoscenza dei concetti di rapporto e di proporzionalità (diretta - su quella inversa vedi più avanti inversa proporzionalità).

Sottolineiamo l'importanza che gli alunni acquisiscano la capacità di passare "spontaneamente" da una forma di rappresentazione all'altra dei rapporti d'uso più comune (0.75, 3/4, 75%; 0.125, 1/8, 12.5%; 15/60, 1/4, 25%; 2/3, 40/60, 0.666…, 67%; …), anche attraverso esercizi ripetitivi che ne consolidino le varie rappresentazioni grafiche (diagrammi a striscia, a colonne e a settori circolari, variamente graduati, rettangoli di ugual forma, rette passanti per l'origine). E che padroneggino l'equivalenza tra divisione per contenenza e divisione per partizione per rendersi conto immediatamente, ad es., che 1/0.1 è 10 in quanto 0.1 sta 10 volte in 1, e per sviluppare/consolidare meglio l'idea che il reciproco del reciproco di un numero è il numero stesso e quella che "moltiplicare per 1/k" equivale a "dividere per k", modi entrambi per esprimere la funzione inversa di "moltiplicare per k".
È fondamentale che gli alunni abbiano chiaro che "%" sta per "/100", che sappiano esprimere le variazioni percentuali come moltiplicazioni (aumento del 10% come moltiplicazione per 1+10/100 = 1.1, diminuzione del 20% come moltiplicazione per 0.8) e che impostino in questo modo i calcoli con le calcolatrici: la cosa è importante per la messa a fuoco che variazioni percentuali successive non si compongono facendone la somma, che, fatto un aumento del P%, per tornare al valore iniziale non si deve fare una diminuzione del P%, che la variazione di P punti percentuali non equivale a una variazione del P%.
Le considerazioni svolte rimandano, evidentemente,
all'uso del concetto di funzione,
che deve essere utilizzato costantemente, riprendendo operativamente le conoscenze sviluppate
nella scuola di base. La rappresentazione grafica della proporzionalità (diretta) e quella di fenomeni
in cui la variazione di una grandezza è proporzionale a quella di un'altra forniscono il
contesto naturale in cui passare dalla pendenza "fisica" a quella "matematica"
(vedi variazione e pendenza)
e riprendere e precisare il concetto di funzione lineare e il legame tra
soluzione grafica e simbolica rispetto a x delle equazioni del tipo
È anche un contesto molto naturale per la ripresa e il consolidamento delle prime attività di manipolazioni
di formule. Sottolineiamo l'inopportunità di ricorrere a tecniche risolutive specifiche per le proporzioni (invece
che considerarle equazioni come le altre) per affrontare problemi di proporzionalità. Se qualche alunno, come retaggio di
precedenti "cattivi" insegnamenti, propone proporzioni del tipo
angolo dato dato
—————— = —————— —> angolo = ——————·360
360 totale totale Per tracciare diagrammi di vario tipo (vedi variazione e pendenza) occorre mettere a fuoco il ruolo dei fattori di scala. Si tratta di un aspetto importantissimo, non solo per l'interpretazione delle rappresentazioni grafiche delle statistiche (e per introdurre considerazioni/attenzioni che saranno utili per la costruzione e lettura delle rappresentazioni grafiche di distribuzioni statistiche riferite ad intervalli di ampiezza diversa), ma anche per padroneggiare le unità di misura di aree e volumi e il passaggio da un'unità all'altra, e per effettuare stime; esso entra, inoltre, in gioco in molte altre questioni di Fisica e di Biologia, oltre che di Matematica. | 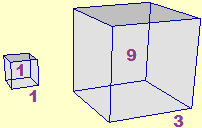 |
Il concetto di frazione è bene che sia presentato come un caso particolare di rapporto: questo consente di intrecciare bene i diversi aspetti con cui le frazioni si incontrano nelle applicazioni. L'"algebra delle frazioni" può essere discussa successivamente (vedi strutture matematiche): prima è necessario mettere a fuoco come confrontare rapporti, come determinare il reciproco di un rapporto e, poi, l'uso della proprietà distributiva (vedi formule, termini, grafi).
Ovviamente, anche il contesto delle rappresentazioni proporzionali offre semplici e significative occasioni per educare all'uso di strumenti informatici per l'automazione parziale o totale dei procedimenti di calcolo.
Come dovrebbe accadere per l'introduzione di tutti i
modelli matematici, è bene che anche nel caso dei concetti discussi qui si mettano
in luce non solo i vantaggi del loro impiego, ma anche i limiti: le informazioni che si perdono confrontando percentuali invece che dati assoluti,
l'accortezza con cui devono essere interpretati i confronti tra l'evoluzione di diversi fenomeni
basati sulla loro rappresentazione mediante numeri indici o variazioni relative, ... Nel caso in cui si impieghi, ad es., un foglio
elettronico, occorre mettere in guardia dagli errori di rappresentazione/interpretazione
che può indurre un uso non critico dei suoi menu (vedi QUI).
L'uso delle varie rappresentazioni grafiche (linea dei numeri, grafici, grafi ad albero, istogrammi, schemi, ...)
facilita notevolmente i ragionamenti,
l'inquadramento dei problemi, la ricerca e congettura di strategie risolutive,
l'esplorazione di nessi, relazioni o regolarità,
la visualizzazione di grandi quantità di informazioni,
la messa a punto di modelli che consentano
facilità di passaggio tra contesto e concetti con cui esso è matematizzato, …
È anche il modo attraverso cui le elaborazioni matematiche (relative a
indagini sociologiche, situazioni economiche, fenomeni tecnico-scientifici, …)
ci vengono in genere comunicate dai mass media.
Le rappresentazioni grafiche sono sempre più presenti
nei vari settori della matematica. E molti dei concetti più astratti
nascono come generalizzazioni di concetti spaziali, di cui portano traccia,
metaforicamente, nel loro nome (spazi di funzioni, spazi di dimensioni infinite, metriche su spazi astratti,
misure di insiemi astratti, ... e punti, coordinate, diametri,
proiezioni, ortogonalità, ... riferite a oggetti che non possiamo rappresentare fisicamente).
È quindi fondamentale che l'insegnamento educhi all'uso delle rappresentazioni grafiche (sia per modellizzare situazioni che per svolgere considerazioni teoriche), al transfert tra esse ed altre forme di rappresentazione, all'intreccio tra metodi grafici e metodi simbolici e numerici, ...
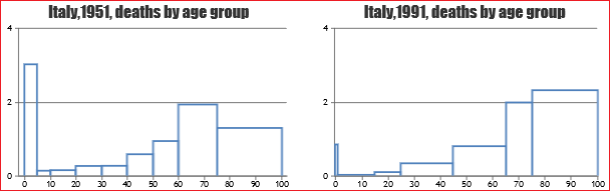
È opportuno che sin dalle prime lezioni, intrecciandosi a considerazioni di statistica, geometria e ad analisi di vari fenomeni, si introducano le principali forme di rappresentazione grafica (evidenziandone potenzialità, limiti e problemi interpretativi - vedi, a destra, diverse rappresentazioni delle migliaia di disoccupati al passare degli anni). Approfondimenti specifici sul piano cartesiano e sulle curve potranno essere svolti successivamente. | 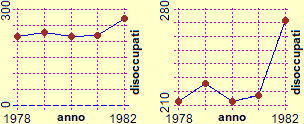 |
Il computer è uno straordinario strumento che facilita la
costruzione (e la lettura) di molti tipi di rappresentazioni grafiche.
Esiste molto software d'uso gratuito che può essere d'aiuto in questo senso.
È tuttavia importante che gli alunni imparino innanzi tutto a tracciare a mano grafici,
a partire sia da dati che da rappresentazioni algebriche, che acquisiscano la capacità di schizzare, con
la accuratezza necessaria a seconda del contesto, i grafici delle principali funzioni man mano studiate,
..., e che diventino in grado di immaginarsi grafici, di descriverli a parole, ..., oltre che schematizzare graficamente
problemi, rappresentare con grafi termini e procedimenti, associare grafici a fenomeni, ...
L'argomento "approssimazioni" deve essere introdotto gradualmente all'interno di tutte le attività didattiche che si presentano, senza una trattazione a sé stante, in quanto a seconda dei contesti sono vari i modi in cui si presenta: leggere e interpretare dati approssimati che si trovano su articoli, alla televisione, …; distinguere i diversi modi più o meno formalizzati in cui le approssimazioni sono presentate; saper leggere misure con i vari strumenti e descriverle matematicamente; comprendere la differenza tra arrotondamenti e approssimazioni per troncamento e i modi diversi con cui operare con esse; approssimare i risultati di operazioni e procedimenti vari ottenuti con un mezzo di calcolo (su questo aspetto vedi anche calcolatrici, calcolatore, logica); leggere/rappresentare graficamente informazioni che dipendono da dati approssimati; …
Il tema deve poi essere ripreso negli ultimi anni delle superiori, collegato a tematiche matematiche più generali (il calcolo differenziale, le approssimazioni di curve, le approssimazioni di calcoli probabilistici effettuati mediante simulazioni statistiche, …), nonché a tematiche fisiche (per avere un'idea dei collegamenti con la fisica vedi QUI).
Richiamiamo i significati correnti di troncamento, arrotondamento e cifre significative:
| |||||||||
L'ultimo esempio sopra fatto mette in luce anche l'utilità della notazione esponenziale: per chiarire che 1400 è l'arrotondamento a 3 cifre di 13.961 (non solo quello a 2 cifre) ci si può esprimere usando la notazione scientifica 1.40·10³. Occorre, però, far osservare anche che un mezzo di calcolo non mette gli zero finali …
Qualche precisazione tecnica.
Il termine matematico arrotondamento, ad essere rigorosi, non è nato come
sinonimo di "approssimazione al numero (intero o …) più
vicino", ma per indicare una approssimazione con un numero
inferiore di cifre (come suggerisce anche l'etimologia della parola).
Tuttavia negli ultimi decenni si è diffusa questa
interpretazione, per distinguere in modo chiaro "arrotondamento" e "troncamento".
Si noti, però, che spesso si usa la parola
"arrotondamento" anche nell'accezione più estesa; ad
esempio parlando di errori o problemi di arrotondamento nel calcolo
automatico ci si riferisce ai fenomeni conseguenti alle approssimazioni
con meno cifre effettuate dalle macchine, indipendentemente dal modo in cui queste approssimazioni vengono svolte.
Il
concetto di cifre significative viene spesso usato anche in
un'accezione più estesa.
Ad esempio si parla di arrotondamento a n
cifre significative anche in situazioni in cui si arrotonda a meno
di un'unità sulla n-esima cifra iniziale (non a meno di
1/2 unità, come si è fatto qui): se una bilancia
garantita con la precisione di 1 grammo dà il peso 160 g si
può dire che questo ha 3 cifre significative, intendendo che
il peso è 160±1 g, cioè cade in [159 g, 161 g];
se la bilancia avesse la precisione di 10 grammi diremmo che il peso
160 g ha 2 cifre significative, intendendo che è 160±10.
In questi casi è, comunque, norma indicare la precisione.
Si potrebbe anche approssimare alla cinquantina più
vicina: 1867 verrebbe arrotondato a 1850 e le cifre significative
sarebbero 3 (185).
Più
in generale, a volte si parla di n cifre significative anche
nel caso di un'approssimazione in cui si abbia qualche
informazione sull'n-esima cifra iniziale, cioè in
cui si sappia solamente delimitare i valori che può assumere
l'n-esima cifra iniziale (ad esempio nel caso si ottenga il
valore 34.6178 e si sappia che l'errore è al più di
0.03, si può concludere che la 4a cifra iniziale non è
una cifra qualunque: il numero deve finire con 58, 59, …,
o 64; della 5a cifra iniziale non possiamo invece dire
nulla; a volte, dunque, si dice che le cifre significative sono 4,
cioè 34.62, anche se ad essere precisi potremmo scrivere
solamente 34.62±0.04, in modo da comprendere tutto
l'intervallo 34.6178±0.03).
È importante sottolineare agli alunni la convenienza di effettuare solo
alla fine gli arrotondamenti. Si tratta, comunque, di un'abitudine
da consolidare attraverso la pratica (e l'uso, ragionato, dei mezzi di calcolo,
sin dalla scuola primaria). Un tempo (fino al 1970 circa) quando si procedeva
con il calcolo manuale, era più comodo operare su
arrotondamenti dei risultati intermedi, anche se si peggiorava la
precisione del risultato. Cose del genere, tuttavia, mezzo secolo dopo, si trovano ancora in molti manuali sia di fisica che di matematica!
È, anche, utile far osservare (e verificare) agli alunni che se si consulta in rete materiale in lingua inglese al posto
di sensibilità (di uno strumento, di una misura) si usa sensitivity.
Date le approssimazioni per eccesso e per difetto dei dati, si può trovare automaticamente il risultato approssimato delle 4 operazioni e dell'elevamento a potenza trovando il minimo e il massimo dei 4 risultati ottenuti operando sulle diverse approssimazioni con un semplice programmino; ecco ad esempio che cosa si può ottenere con questo, eseguibile da rete (un rettangolo con lati compresi tra 3.8 e 3.9 cm e tra 6.4 e 6.5 cm ha area compresa tra 24.32 e 25.35 cm², con indeterminazione di 1.03 cm²; se so che x = 0.9±0.05 e che y è compreso tra 1.39 e 1.40 posso concludere che xy è compreso tra 0.7965 e 0.9312, con indeterminazione 0.1347; la metà di 50±0.5 g è compresa tra 24.75 e 25.25 g, con indeterminazione di 0.5 g; l'indeterminazione - uncertainty in inglese - è la differenza tra le due approssimazioni).
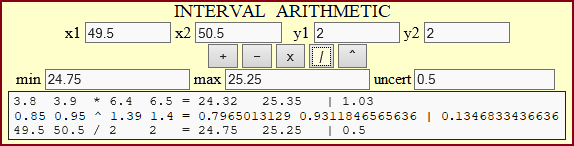
In casi più complessi si può ricorrere al generatore di numeri casuali per trovare il risultato con una
sperimentazione numerica, in modo più preciso e affidabile che con le tecniche di calcolo differenziale spesso usate. Vedi ad esempio QUI.
| Gli strumenti graduati sono in genere costruiti in modo che l'ampiezza di una divisione corrisponda alla sensibilità dello strumento, ossia alla minima variazione della grandezza misurata che fa variare il valore indicato dallo strumento; in questi casi precisione e sensibilità possono essere considerati come sinonimi. Ma non è sempre così: in alcuni casi al più piccolo stimolo che lo strumento percepisce il valore indicato si modifica di più di una divisione; un fenomeno analogo si verifica spesso con gli strumenti in cui le misure sono espresse digitalmente: per misure di un certo ordine di grandezza alla più piccola variazione le ultime cifre variano di molte unità (in questi casi la precisione dello strumento può essere molto maggiore, ossia molto peggiore, rispetto al valore che corrisponde alle variazioni della cifra più a destra), mentre per misure di altri ordini di grandezza lo stesso strumento si può comportare in maniera opposta (l'ultima cifra scatta più lentamente rispetto alle variazioni che lo strumento in realtà percepisce). | |
| In fisica spesso si fa una distinzione tra misura precisa e misura accurata: una misura x con ideterminazione Δx di una grandezza x è tanto più accurata quanto più x è vicino al valore esatto di x, è tanto più precisa quanto più Δx è piccolo. Questa distinzione rende conto del fatto che, in una attività di misurazione, possono essere presenti degli errori sistematici, dovuti ad un difetto di impostazione [ad esempio l'uso di una bilancia ad ago in cui l'ago a riposo non è posizionato su 0 o di una riga graduata in cui le divisioni sono più ampie del dovuto], che fanno sì che le misure ottenute, per quanto "precise", siano comunque affette da uno scarto dal valore esatto. In questa voce, quando facciamo degli esempi riferiti alla fisica, supponiamo sempre che si tratti di misure accurate, ossia che le approssimazioni siano effettive approssimazioni del valore esatto. La figura a lato illustra metaforicamente il comportamento di apparati misuratori molto sensibili con diversi gradi di precisione e accuratezza (i valori esatti sono il "centro" dei bersagli). | 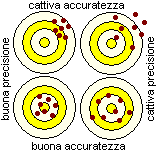 |
Calcolatrici. Calcolatore. Logica
È opportuno, sin dalla scuola di base, fare un ampio uso delle calcolatrici tascabili (CT). Può essere utile all'insegnante fare una rassegna delle CT di cui dispongono gli alunni (ad esempio può farsi consegnare dagli alunni un foglio su cui abbiano disegnato la tastiera della propria CT). E`, poi, il caso di invitare gli alunni a leggere il manuale d'uso della propria CT (escludendo inizialmente i tasti per le funzioni più complesse). Ricordiamo che l'uso delle calcolatrici è indispensabile nel caso siano presenti alunni con difficoltà di tipo discalculico, come ricordato nella voce le operazioni aritimetiche.
Gli obiettivi dovrebbero essere sia quello di acquisire una maggiore padronanza di questo mezzo di calcolo, comprenderne i limiti al fine di interpretare i risultati che fornisce, …, sia quello di introdurre e/o consolidare (a un primo livello) alcune conoscenze matematiche: sui numeri (approssimazioni, numeri reali, …), sulle funzioni (funzioni a più input e più output, composizione di funzioni, funzioni inverse, insieme di definizione, …, funzioni circolari, …), …, sia quello di preparare il terreno per la comprensione del funzionamento dei calcolatori (che, come "conoscenze" matematiche e possibilità di calcolo aritmetico non si discostano "essenzialmente" da una CT).
È evidente come l'uso dei mezzi di calcolo sia da introdurre e sviluppare contestualmente alla trattazione degli altri temi matematici, pur con degli approfondimenti specifici. Esempi di attività in questa direzione possono essere suggeriti dagli esercizi presenti QUI (e nelle pagine successive), in cui il tema viene allargato a quello della descrizione degli algoritmi e alla descrizione e riflessione di vari aspetti dei processi di automazione, tema al quale - data la centralità che ha assunto nel normale lavoro di quasi tutti i matematici e di chi usa la matematica in altre discipline, tecniche o mestieri - va dato anche uno spazio autonomo, che può poi suggerire ulteriori sviluppi matematici; qualche spunto in questo senso può essere suggerito dal materiale presente QUI. Qualche esempio di software di vario genere si può trovare QUI. Sotto un esempio: una "calcolatrice tascabile".
L'avvio all'uso dei linguaggi di programmazione e di altro software comporta anche la
discussione delle analogie e delle differenze tra linguaggio formale e linguaggi artificiali. Un aspetto collegato è
la discussione di che cosa del tema logica possa essere affrontato a livello scolastico;
questo tema non può che essere inteso in senso lato, come educazione
all'attenzione agli aspetti linguistici, all'esposizione comprensibile delle argomentazioni, ….
Gli operatori logici sono da intendere come elementi necessari per costruire funzioni e relazioni da descrivere ed elaborare formalmente,
non certo come elementi per costruire formule da studiare in ambiti di logica formale, area della matematica non affrontabile
(se non caricaturalmente) negli studi pre-universitari (vedi QUI).
Val la pena ricordare che anche le dimostrazioni non possono essere incluse in un'area specifica di apprendimento:
esse sono diffuse in tutte le aree della matematica e le tecniche dimostrative (e i modi in cui sono espresse le proposizioni
matematiche da dimostrare) sono numerosissime, non racchiudibili in qualche esempio stereotipato, come spesso avviene nei libri di testo
(una riflessione su che cosa siano le dimostrazioni può essere trovata QUI;
qualche esempio di attività sull'area della logica e delle dimostrazioni può essere trovato
QUI, e nelle pagine successive).
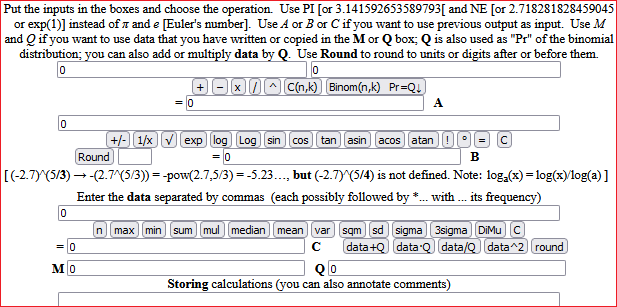
Come già osservato per la scuola secondaria di 1º grado, vanno messe a fuoco le differenze tra argomentazioni intuitive e dimostrazioni. Ad esempio nel caso seguente in cui il quadrato grosso ha un vertice nel centro del quadrato piccolo (figura A) posso supporre che la parte in comune ai due quadrati sia circa un quarto del quadrato piccolo, posso ritenere che le cose stiano esattamente così pensando al fatto che ruotando il quadrato grosso posso arrivare alla figura B, ma per dimostrare che questo vale in generale devo fare il ragionamento illustrato nella figura C.
E, come già osservato, va curata la costruzione dei concetti e del linguaggio matematico, e del significato delle definizioni, più che la memorizzazione di definizioni, spesso sbagliate. Clamorose sono le definzioni errate di parallelismo diffuse in molti libri di testo: vedi qui.
Devono, poi, essere evidenziati, anche all'inizio della scuola secondaria di 2º grado, i conflitti tra terminologia matematica e linguaggio comune, specie in ambito geometrico: i diversi significati di angolo, direzione, distanza, curva, ... e di molte parole d'uso frequente; si pensi che nella normale comunicazione quando si parla di tavolo rettangolare si intende uno che non sia quadrato, mentre in matematica i rettangoli sono particolari quadrati. Ciò rimanda anche al modo in cui i concetti sono definiti: se dico che un triangolo isoscele è un triangolo che ha due lati eguali intendendo che anche i triangoli equilateri sono iscosceli, sottointendo che "due" stia per "almeno due", non per "esattamente due"; per l'adulto "colto" questo è scontato, per l'alunno no; l'insegnante deve esplorare l'eventuale esistenza di misconcezioni di questo genere. Si pensi poi ai molti significati che la parola uguale ha in matematica, del tutto diversi da quello, profondamente errato, che le viene attribuito da molti libri ("uguale" come "essere la stessa cosa"): vedi i molti esempi presentati qui.
Nota. Se l'insegnante vuole può mettere in rete grafici realizzati con un semplice script e che gli alunni possono ridimensionare liberamente col mouse (vedi QUI):
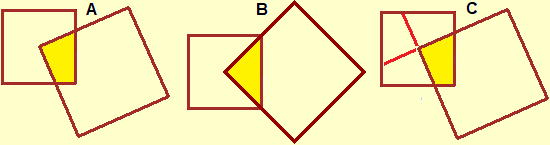
La statistica descrittiva, a cui abbiamo accennato più volte discutendo dei temi precedenti, e in particolare alla voce i concetti di rapporto e proporzionalità, si presta all'introduzione o revisione in contesti significativi di molti concetti matematici di base, dai numeri al calcolo approssimato, dal concetto di funzione alla costruzione e uso delle formule, dalle rappresentazioni grafiche di relazioni numeriche alla lettura e messa a punto di algoritmi. Questo, almeno, se non viene ridotta ad essere un tema in più da insegnare separatamente dagli altri temi. Gli strumenti di statistica descrittiva servono poi come punti di riferimento per la successiva introduzione alla probabilità (concetto di distribuzione, proprietà della funzione-probabilità, …). QUI sono presenti link a programmi impiegabili per elaborazioni statistiche. Accenniamo ad un paio di osservazioni importanti da affrontare con gli alunni. La prima è che la somma di tre o più frequenze percentuali approssimate non è detto che faccia 100: se ho un totale di 150 ripartito in tre parti ciascuna pari a 50, la frequenza percentuale di ognuna di esse è 33% o 33.3% o …; la loro somma non è 100. La seconda è che ci sono diversi concetti di "media" oltre alla media aritmetica. Oltre al ruolo importantissimo della mediana è importante mettere a fuoco che la velocità media non si ottiene facendo la media aritmetica di più velocità. |  |
È opportuno mettere a fuoco, poi, che in un istogramma (come quello sopra a destra) le frequenze delle varie classi sono rappresentate dalle aree dei rettangolini, non dalle loro altezze! Questo aspetto sarà importante, poi, per affrontare nelle classi successive (senza misconcetti) lo studio delle variabili casuali continue usando l'integrazione (se la distribuzione è rappresentata da una curva, la probabilità che l'uscita sia tra A e B è l'area sottesa al grafico tra le ascisse A e B).
I contesti a cui riferire le indagini statistiche sono innumerevoli. È comunque opportuno fare riferimento anche a temi vicini ai bisogni conoscitivi (e psicologici) dei ragazzi di questa fascia di età (la società, lo sviluppo corporeo, la scuola, …).
Altre attività di tipo statistico possono essere svolte anche nell'ambito del laboratorio fisico chimico.
Bisogna però tener presente che esse possono aver senso solo nell'ambito di apparati misuratori ad alta sensibilità:
gli usuali strumenti di misura per le lunghezze (metro, calibro, palmer, …), per il peso (bilance a molla e simili), per la temperatura (termometro), per il tempo (orologio, cronometro, …) … sono a bassa
sensibilità, cioè l'indeterminazione coincide con la sensibilità dello strumento (cioè con la massima differenza apprezzabile utilizzando la graduazione o le cifre visualizzate), per cui non ha alcun senso fare delle statistiche su misure che, se la misurazione
è fatta con cura, devono ripetersi uguali (o al massimo con un'incertezza sull'ultima cifra nel caso di misure che siano a metà tra due tacche
- se si arrotonda - o a cavallo di una tacca - se si tronca).
Può essere ritenuto ad alta sensibilità l'apparato misuratore per intervalli di tempo costituito da un cronometro che rileva i centesimi di secondo ma che è
azionato a mano:
in tal caso la componente dell'apparato che governa l'avvio e l'arresto introduce degli errori casuali che hanno ordine di grandezza maggiore della sensibilità del cronometro,
per cui può essere opportuno che la misura sia effettuata contemporaneamente da più persone e poi sia fatta un'analisi statistica
dei vari rilevamenti. Si può poi scegliere una coppia di percentili da assumere come estremi dell'intervallo di indeterminazione, ad
esempio il 25º: e il 75º: percentile (questa scelta corrisponde, grosso modo, all'idea di prendere l'intervallo dei valori tale che,
se si effettua una nuova misura, c'è il 50% di probabilità che essa vi cada dentro). L'argomento è da riprendere
e approfondire nella seconda parte delle scuole superiori, usando concetti probabilisitici.
All'inizio, dunque, è bene operare, anche nell'ambito fisico chimico, con misure a bassa sensibilità.
Dell'introduzione di questi concetti abbiamo già discusso più volte riflettendo sullo sviluppo dei concetti di rapporto e proporzionalità.
È fondamentale intrecciare tutti questi concetti alla rappresentazione grafica della proporzionalità (e delle funzioni lineari), mettere in luce la diversità tra variazioni assolute e variazioni relative, mettere a fuoco come queste ultime sono rappresentabili/interpretabili come dei prodotti, ….
aumento del 10% aumento del 20% x ———————————————> x·(1+10/100) ———————————————> x·(1+10/100)·(1+20/100) = x·1.1·1.2 = x·1.32 |
Questo lavoro serve, per altro, a costruire dei presupposti
per la risoluzione delle equazioni, per lo studio della geometria, per l'introduzione di elementi di geometria tridimensionale e,
infine, per l'introduzione del concetto di "derivata".
Di variabili, costanti, termini abbiamo più volte parlato discutendo delle voci precedenti (in particolare alle voci concetto di modello e operazioni aritmetiche) e ne parleremo nelle voci successive (a partire dalla prossima), in quanto si tratta di concetti e aspetti linguistici di base (legati alla scrittura, interpretazione e modificazione delle formule), a cui comunque occorre dare, ad un certo punto, una prima sistemazione, decisamente diversa dal modo "buffo" di avviare il calcolo algebrico usato spesso nei libri di testo (introduzione di strane cose chiamate polinomi, che tali non sono [vedi la voce funzioni polinomiali], mancanza di collegamenti con gli usi per rappresentare e risolvere equazioni, …).
Ricordiamo l'importanza di richiamare dai livelli scolastici precedenti, o di introdurre, l'uso dei "grafi ad albero", importante per imparare il significato delle formule, imparare a passare da un linguaggio all'altro, leggere le formule non solo come sequenze di simboli, consolidare le prime convenzioni nella scrittura dei termini, … e per descrivere procedimenti non facilmente descrivibili come formule, per risolvere problemi, ...

Occorre puntare molto sull'analisi della struttura dei
termini, pensando che difficoltà relative a questo aspetto siano all'origine di molti dei più comuni errori degli
alunni. Si devono, poi, stimolare gli alunni a individuare,
esplicitare e controllare i procedimenti di trasformazione man mano impiegati nei vari passaggi.
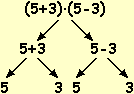
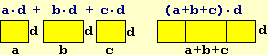
L'obiettivo non è quello di dimostrare agli alunni tutti i procedimenti di
trasformazione algebrica; ad esempio piuttosto che la proprietà associativa è meglio mettere a fuoco direttamente la
"proprietà del riordino" (illustrata nelle prime due figure seguenti), che non sarebbe stato affatto banale dimostrare a partire
dall'associatività e dalla commutatività (proprietà
che per altro richiederebbero a loro volta una giustificazione, riferita agli algoritmi per le operazioni, ma assai complessa, o di tipo assiomatico).
L'obiettivo è piuttosto quello di far svolgere il calcolo algebrico avendo
chiari i sottotermini su cui si opera, anche, inizialmente, facendo rappresentare i termini mediante grafi ad albero, e mettere in luce contesti chiari,
in genere di tipo geometrico, che giustifichino le proprietà di base.

È importante poi notare che i metodi grafici consentono di anticipare, e poi motivare, tecniche di tipo algebrico. Un esempio:
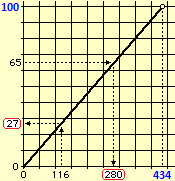 |
Quale "percentuale" di 434 è 116?
dato 65 dato
65 = ———— ·100 → ——— = ———— →
434 100 434
65 65·434
——— ·434 = dato → dato = —————— = 282.1
100 100
|
Per qualche considerazione storica e didattica sull'uso delle formule e sull'algebra elementare vedi QUI, dove sono commentati anche alcuni grossolani errori spesso presenti nelle definizioni che si trovano nei libri scolastici.
Anche le riflessioni sul simbolo "=" e sui suoi diversi usi in matematica devono trovare spazio nell'insegnamento, per evitare o superare misconcezioni. Vedi QUI per qualche esempio e qualche considerazione didattica.
Osserviamo che in alcuni libri di testo si parla di radicali aritmetici.
È uno strano concetto che ha poco a che fare col concetto che, un tempo, si usava individuare
con tale termine, per distinguerlo dai radicali algebrici: col primo
si indicava quella che viene chiamata semplicemente "radice",
col secondo si indicava l'insieme delle soluzioni di un'equazione (con incognita x)
del tipo xn = k; ad es. nel caso di x2=4 si
avrebbe {−2,2}. In questi libri viene chiamato radicale aritmetico
la radice solo dei numeri non negativi. Quindi
I concetti di funzione e di risoluzione di un'equazione
I concetti di funzione ed equazione sono forse i concetti più importanti della matematica; si intrecciano con quasi tutte le altre voci qui discusse. Essi sono presenti nei programmi di tutti i livelli scolastici. Evidentemente si tratta di concetti che sono a monte del concetto di polinomio e sorprende che in molti libri di testo questo sia introdotto prima (sul modo, purtroppo buffo, in cui avviene questa introduzione ci si sofferma nella specifica voce funzioni polinomiali).
Le prime funzioni che i ragazzi incontrano esplicitamente sono, all'inizio della scuola elementare, le quattro operazioni (a due input), gli incrementi e decrementi unitari e il cambio segno (ad un input). Ma alla scuola elementare incontrano anche funzioni con quantità qualunque di input, come il massimo e il minimo di un insieme di dati, e funzioni a cui non corrisponde un procedimento di calcolo (per esempio la altezza o il peso di una persona, o la popolazione di una città, al passare del tempo, o tariffari di vario genere, in cui il valore monetario è espresso in funzione di varie grandezze). Incontrano anche funzioni a più output (la divisone con resto, per esempio, è una funzione a due input e due output).
Del resto sono funzioni anche gli istogrammi a crocette, che possono essere affrontati anche prima della scuola elementare, nella scuola dell'infanzia, come quelli presenti QUI: ad ogni modo di arrivare a scuola viene associato il numero (rappresentato da una colonna di di crocette) degli alunni che lo utilizza, ad ogni tipo di località delle vacanze viene associato il numero degli alunni che le ha passate in quel modo, ad ogni condizione del tempo viene associato il numero dei giorni del mese in cui il tempo è stato tale, …
È evidente che questi concetti hanno poco a che fare con le definizioni con
cui essi vengono introdotti in molti libri di testo: una funzione è un insieme di coppie ordinate
tale che …; gli autori di tali libri hanno orecchiato definizioni come questa che si fanno
nei corsi universitari di algebra, senza rendersi conto che per padroneggiarle
occorre disporre delle tecniche, non semplici, per rappresentare una sequenza di
input ed una sequenza di output con una opportuna coppia di oggetti matematici.
Occorre costruire, in modo adeguato, la possibilità e l'opportunità
di presentare le funzioni come insiemi di coppie
Ricordiamo che il nome "operazione" è un appellativo usato per indicare alcune funzioni, in genere ad 1 o 2 input, ma non solo. Non esiste una "definizione" del concetto
di operazione.
Val la pena ricordare che le funzioni erano introdotte nella scuola media inferiore italiana da Emma Castelnuovo subito dopo la seconda guerra mondiale e che in molti libri e articoli sosteneva che esse vanno introdotte sin dai primi anni di scuola: "Si chiederà: quando trattare questo argomento? come introdurre il concetto di funzione? Sono forse troppo decisa e rivoluzionaria se a questa domanda rispondo da sempre? Non è che intendo che a questo argomento si debba dedicare un certo numero di lezioni, ma esso deve essere introdotto così, insensibilmente, a proposito di una questione o dell'altra, perché esso entra in ogni questione." (vedi QUI) Chi ritiene che debba essere introdotto solo nella scuola superiore, magari neanche nel primo anno, è solo "ignorante" (di "matematica", si intende).
Rinviamo al documento sulla scuola media inferiore per un'idea di come potrebbe essere stato sviluppato il concetto di funzione in quel livello scolastico, e di come potrebbe essere eventualmente ripreso all'inzio della scuola superiore.
È importante che gli alunni consolidino il "concetto" di funzione (non che ne memorizzino una "definizione") facendo riferimento a vari modi di
esprimerlo o rappresentarlo (numerici, grafici, algebrici, a parole, …),
e rinsaldando, gradualmente, e quando è possibile, l'intreccio tra questi modi.
È fondamentale che gli alunni riprendano subito e consolidino
il significato di radice quadrata (che non può essere altro che definita
subito facendo riferimento ai numeri reali, intesi e introdotti come numeri decimali, i numeri
che si usano e il cui significato è da riprendere dalla scuola media:
i numeri razionali - non le frazioni - ovviamente devono essere introdotti dopo, come sottostruttura
dei numeri reali, che gode di particolari proprietà algebriche).
Gli alunni devono poi essere abituati sin da subito a rappresentare grafici di funzioni continue e discontinue (senza
introdurre termini specifici per distinguerle) col fine di evitare che essi tendano a identificare le funzioni
con le sole funzioni continue.
È, poi, decisivo, ai nostri giorni, l'uso delle calcolatrici tascabili, e quindi quello del computer, per i quali rinviamo ad una specifica voce.
È bene indicare le variabili in vari modi,
come accade nelle vita di tutti i giorni. A questi usi deve seguire, poi, gradualmente, l'esercizio e il
consolidamento astratto, che si può fare su variabili con nomi che prescindono
dai vari contesti applicativi. Ed è bene rendersi conto, subito, che una
formula può essere trasformata esprimendo una variabile in funzione di altre
in modi diversi, a seconda delle esigenze. È poi fondamentale fare riferimento
al concetto di funzione inversa, come strumento per smontare/trasformare equazioni.
Rinviamo al documento sulla scuola media inferiore per un'idea di come potrebbe essere stata sviluppata la risoluzione delle equazioni in quel livello scolastico, e di come
potrebbe essere eventualmente ripresa all'inzio della scuola superiore.
Si noti l'importanza, soprattutto nelle fase iniziale, di usare
modi informali di esprimersi e, quando si ricorre ad espressioni più
formali o formalizzate, di farlo con un certo rigore: certi usi scorretti
appresi all'inizio sono fonte/alimento di profondi misconcetti che, poi,
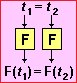
è difficile smontare. Ad esempio è bene fare osservare che se F è una funzione
Le riflessioni sui concetti di funzione ed equazione sono spesso intrecciate all'uso di software, per il calcolo e per la rappresentazione grafica; se non si dispone di un'aula computer si possono fare delle presentazioni in aula su come lo si può usare, lasciando poi agli alunni un uso a casa dello stesso. Chi non possa usare l'aula computer ma disponga di calcolatrici o pocket computer con schermo grafico può svolgere attività analoghe utilizzando i programmi di grafica incorporati in questi mezzi di calcolo; altrimenti: CT per i calcoli e … carta millimetrata e matita!. Carta e penna sono comunque indispensabili anche per usare il software proposto: sia per annotare dati, espressioni, …, sia per prendere appunti mentre si "ragiona" su come usarlo (individuazione di strategie, scelta di comandi e di dati da introdurre, …): i programmi sono solo un "sussidio", anche se a volte indispensabile.
Occorre illustrare o sfruttare didatticamente l'analogia delle schematizzazioni della composizione di funzioni con l'impiego di grafi e diagrammi in diversi ambiti, considerati in altre voci.
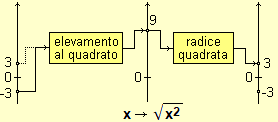 |  |  |
Occorre, subito dopo, mettere a fuoco le analogie e le differenze tra le funzioni x → xn con n intero pari e quelle con n intero dispari, in relazione alla simmetria rispetto all'asse verticale o rispetto all'origine degli assi, e in relazione al ribaltamento attorno alla bisettrice del primo quadrante.
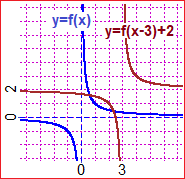
Va introdotto gradualmente, senza inizialmente approfondirne i limiti, il procedimento di "applicare a entrambi i membri una stessa funzione" per risolvere equazioni.
(A-2)/5 = 1/4 applico u → u·5
A-2 = 5/4 applico u → u+2
A = 5/4+2 = 4.25
|  | √(2x+5) = x+1 applico u → u²
2x+5 = x²+2x+1 applico u → u-2x-1
4 = x²
x = ±2 ma -2 non è una soluzione
u → u² non è iniettiva |
Occorre consolidare il concetto di dominio di una funzione, mettendo a fuoco che quando si modellizza una situazione problematica
occorre considerare solo gli intervalli in cui possono variare le grandezze rappresentate dalle variabili (come nel caso della funzione V considerata poco sopra,
in cui occorre restringersi a
− devono essere forniti gli elementi generali necessari per studiare, ad un primo livello,
le funzioni ad un input ed un output e la risoluzione di equazioni, senza e con parametri;
− si deve essere accennare e far provare l'uso di software di calcolo simbolico, anche quello incorporato
in WolframAlpha; il motivo è,
soprattutto, quello di ridurre (nella testa degli alunni) l'importanza degli aspetti calcolistici:
essere bravi e veloci a fare i calcoli non è né necessario né sufficiente per essere "bravi" in matematica.
Per consentire le prime elaborazioni statistiche e la realizzazione dei primi grafici di funzione
occorre introdurre quasi subito il concetto di intervallo. Occorre anche introdurre il simbolo "∞" e gli aggettivi "aperto",
"chiuso" e "limitato". Gli altri significati, diversi, del termine "infinito" (legati alla cardinalità degli insiemi) è bene siano
introdotti successivamente.
Una riflessione sull'impostazione dell'insegnamento geometrico nella scuola secondaria di 2º: grado è bene che sia affrontata a partire da qualche considerazione generale sull'insegnamento geometrico, che possiamo affidare a questa "digressione", fantastica ma molto concreta, sul concetto di angolo.
Ivi sono contenute varie riflessioni sull'inopportunità di un approccio assiomatico all'insegnamento della geometria. Questo è stato messo a fuoco solo alla fine del XIX secolo, soprattutto con la finalità di mettere a fuoco le diverse geometrie che si potevano definire cambiando alcuni assiomi. I cosiddetti "Elementi di Euclide" (da non confondere con la "geometria euclidea"), significativi nella storia del pensiero, non hanno certo le caratteristiche di quella che, in matematica, è una presentazione assiomatica: QUI è evidenziato come anche le dimostrazioni dei primi "teoremi" di Euclide non siano accettabili.
Gli obiettivi che sarebbe importante privilegiare nelle verifiche iniziali e nelle attivitè di
recupero nel primo biennio (all'inizio della prima classe o prima di affrontare specifici argomenti) dovrebbero essere più
quelli di "atteggiamento cognitivo" e di capacità di "operare" consapevolmente con le conoscenze di base per
risolvere problemi. Ad esempio:
(a) saper usare strumenti di misura (righello, goniometro,
cilindro graduato, bilancia, …) per determinare estensioni (direttamente o misurando altre grandezze fisiche con cui esistano
legami di proporzionalità), saper calcolare l'area di qualche figura "strana" usando quadrettature o mediante
triangolarizzazioni, saper confrontare ad occhio l'ampiezza di angoli disegnati (prescindendo dalle dimensioni dei segmenti con cui
sono sono stati rappresentati i lati), saper associare a una misurazione la corrispondente precisione, avere idea che la
precisione sulle misure dirette influisce sulla precisione delle misure indirette, … più che saper recitare formule
(dirette e inverse) per il calcolo di aree di figure standard, essere addestrati a risolvere problemi stereotipati con coni sovrapposti a
cubi, …;
(b) saper usare strumenti da disegno (tracciare perpendicolari e parallele
usando squadra e riga, …), sapersi organizzare il "foglio di lavoro" (dal problema della scelta delle unità sugli
assi al problema del dove e quali figure disegnare per prime per ottenere una certa figura composta), saper schematizzare con figure
astratte situazioni concrete, saper passare da una descrizione verbale di una figura al suo disegno e viceversa, … più
che ripetere definizioni e saper identificare con disinvoltura figure o elementi di figure disposte in modi "standard";
(c) saper costruire/interpretare riproduzioni in scala (utilizzando equazioni
del tipo y=kx, non con le famigerate regolette ad hoc per le proporzioni), saper calcolare distanze inaccessibili utilizzando
similitudini, saper associare ombre a oggetti e altri trasformati a figure originali, … più
che conoscere i termini "trasformazioni affini", "omotetie", …
(d) aver riflettuto (non genericamente) sulle differenze tra linguaggio
comune e linguaggi specialistici, aver svolto (in contesti semplici, ma non banali) qualche attività di
sperimentazione-congettura-verifica-dimostrazione, avere confidenza con il ricondurre problemi ad altri
problemi (ricondurre problemi di tipo geometrico ad altri problemi di tipo geometrico – sono esempi in questo senso anche alcune delle
attività considerate in (a) –, realizzare o interpretare rappresentazioni grafiche di relazioni tra grandezze, visualizzare
geometricamente proprietà algebriche, …), … più che aver imparato cose del tipo «il punto è l'ente geometrico
senza dimensioni», «non si deve parlare di triangoli uguali ma di triangoli congruenti perché in matematica due oggetti sono uguali solo
se sono la stessa cosa», …
(e) e aver avviato l'affiancamento degli strumenti "diretti" per il disegno (riga, squadra, goniometro, compasso, …) all'uso
del computer (per realizzare disegni sia "a mano libera" che di tipo "geometrico"), mettendo in luce, operativamente, le diverse tecniche e le diverse
idee da usare rispetto all'uso di dispositivi non informatici.
Per esemplificare i livelli più alti di formalizzazione e precisione linguistica, di generalizzazione,
di riflessione "interna", … a cui si deve puntare nel biennio, possiamo citare:
(a) l'uso delle coordinate non solo per rappresentare graficamente dati e funzioni ma come modo di fare geometria,
(b) il teorema di Pitagora non solo per risolvere problemi ma anche come cardine della metrica euclidea,
(c) le trasformazioni geometriche presentate anche analiticamente e mettendo a fuoco (operativamente) il concetto di "invariante".
Non sono molti i concetti e le proprietà che gli alunni devono comprendere e interiorizzare (non imparando a memoria definizioni o dimostrazioni), relativi essenzialmente ai triangoli e ai cerchi.
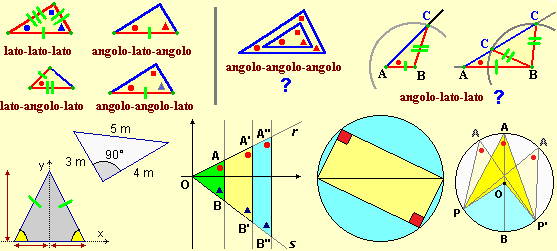
Pur non essendo proponibile una definizione assiomatica del piano (o dello spazio) euclideo, dobbiamo tener conto che è necessario, nella scuola secondaria superiore, dare una presentazione matematica, non solo sperimentale (nel senso "fisico" del termine), della geometria, sia per fornire una visione più esplicita e precisa della natura della matematica, sia per inquadrare meglio il significato delle dimostrazioni.
| La somma degli angoli evidenziati nella figura a sinistra è 360º:. Quanto vale nel caso della figura a destra? Ha lo stesso valore anche nel caso di altri poligoni intrecciati in modo simile, con lo stesso numero di lati? Perché? |  |
| (vedi) |
Per altro, si dovrebbe trovare una impostazione che, rispetto a quella tradizionale, evidenzi meglio lo "stacco" rispetto alla geometria intuitiva, che non è legato solo alla messa a fuoco del ruolo delle dimostrazioni, ma ad una nuova concettualizzazione dello "spazio matematico"; in questo senso pare non soddisfacente un riferimento, troppo ristretto, allo spazio della "fisica" e, soprattutto, di fronte agli enormi sviluppi che ha avuto la matematica e alle molte forme attraverso cui essa si è diffusa nelle professioni e nella vita di tutti i giorni, pare controproducente una estesa e "isolata" trattazione della geometria euclidea.
Anche all'interno della trattazione puramente matematica occorre uscire dal guscio della geometria euclidea, ad esempio accennando all'esistenza di diversi modi per valutare le distanze, come il semplice caso della distanza urbanistica (pari alla somma delle variazioni assolute delle coordinate), calcolabile a mano o con un semplice programmino online, come questo (nel caso illustrato sotto la distanza urbanistica tra (1,3) e (3,5) è 2+2):

Mentre alcuni concetti geometrici vanno introdotti per via analitica:
riferendosi al piano: • punto come coppia di numeri reali, • figura come insieme di punti, • traslazione
come particolare funzione numerica a 2 input e 2 output, • distanza
come opportuna funzione numerica a 4 input 1 output, • direzione
come elemento dell'intervallo [0°,360°), …
per introdurre altri concetti e affrontare problemi e dimostrazioni occorre procedere a volte analiticamente, a volte sinteticamente (ad
esempio una semiretta, invece che analiticamente, mediante un sistema equazione+disequazione, può essere descritta come
l'insieme di punti in cui un punto dato può essere trasformato mediante traslazioni di direzione fissata).
Si tratta di introduzioni che astraggono e generalizzano concetti "fisici" (dalle posizioni su righe e su
superfici individuate con strumenti di misura ai punti come n-uple di numeri, dalle direzioni scandite da un goniometro alla associazione
di un intervallo [a,b) - l'intervallo [0,2π) - ai punti del cerchio x²+y²=1, …), da affrontare dopo lo
svolgimento di riflessioni e attività operative (con strumenti da disegno e di misura) in situazioni "concrete".
Poi, il software di geometria dinamica può favorire questi intrecci e queste astrazioni (si vedano l'esempio precedente e il seguente),
che possono essere sviluppate anche appoggiandosi a gif animati, come questi.
|
Quanto vale la somma delle ampiezze degli angoli opposti di un quadrilatero inscritto in un cerchio? |
 |
| (vedi) |
Il cerchio, in quanto è il luogo geometrico più facile e più "significativo", è un concetto geometrico che va introdotto tra i primi e su di esso poggia l'introduzione di vari altri concetti (direzione, funzioni trigonometriche, …). Le funzioni trigonometriche (anche la funzione tangente) devono essere introdotte precocemente e non solo per gli angoli convessi (scelta che sarebbe difficilmente conciliabile con l'introduzione delle rotazioni, con i riferimenti alle applicazioni extra-matematiche, con l'uso dei mezzi di calcolo, …). Le direzioni (e le misure di angoli) e le misure di aree e lunghezze non possono che essere introdotte mediante un uso non formalizzato del concetto di limite (non con considerazioni su "classi contigue" o simili, difficili da formalizzare in modo rigoroso), in accordo con quanto osservato in precedenza sull'introduzione dei numeri reali).
| Il calcolo della lunghezza dell'arco AP (vedi) | ||
 | 1) considera i punti A e P 2) scrivi la lunghezza della spezzata che congiunge tali punti 3) aggiungi ad ogni coppia di punti successivi il punto del cerchio con ascissa a metà delle loro ascisse 4) torna al punto 2 |
|
I poligoni possono essere definiti come unioni di triangoli, in modo da comprendere anche i poligoni con concavità e i poligoni "intrecciati", e in modo da evitare questioni, non banali, connesse alla suddivisone del piano da parte di linee chiuse (vedi). Le coniche possono essere introdotte a partire dal cerchio e dai grafici delle funzioni x → ax² e x → a/x, utilizzando i movimenti piani. Possono essere introdotte anche altre trasformazioni geometriche, intrecciando in modo opportuno caratterizzazioni sintetiche e analitiche.
 |
Accanto al piano euclideo, si possono presentare subito, senza approfondimenti, altri spazi matematici: spazi finiti, spazi con altre metriche, spazi con altre dimensioni, … per mettere meglio a fuoco la natura "astratta" (e le connesse potenzialità di modellizzazione) dei concetti geometrici. Come già osservato, vanno messe gradualmente a fuoco le differenze tra argomentazioni intuitive e dimostrazioni, ed evidenziati i conflitti tra terminologia matematica e linguaggio comune (i diversi significati di angolo, direzione, distanza, curva, ...).
Negli anni successivi sarà approfondito l'argomento della geometria tridimensionale. Comunque, man mano che vengono introdotti argomenti di geometria piana, è opportuno accennare al loro sviluppo nello spazio, riprendendo e facendo un primo approfondimento di argomenti che dovrebbero già essere stati affrontati nella scuola secondaria di 1º grado (vedi). Ad esempio si dovrà accennare a come con le coordinate si possono rappresentare oltre che punti del piano anche punti dello spazio, a come si legge una cartina con rappresentate le curve di livello, a come gli oggetti tridimensionali possono essere distinti in base alle simmetrie:
|
|
|
|
Nell'ultima figura viene ricordato un tema geometrico citato in altre voci (funzioni circolari,
inversa proporzionalità, strutture matematiche): quello delle traslazioni e dei vettori, che nelle scuole dove lo studio della
fisica è previsto già nel primo biennio deve essere affrontato, ad un primo livello, anche nel caso tridimensionale.
Le immagini seguenti richiamano altri aspetti che possono essere affrontati, con collegamenti ad altre discipline:
la questione delle riproduzioni cartografiche (A conserva le aree, B conserva gli angoli di intersezione, C le traiettorie rettilinee),
il problema degli spostamenti su una superficie non piana (la formica che cammina partendo lungo un "equatore" della palla mantenendosi
perpendicolare ai "meridiani" rimane sull'equatore, quella che parte da un altro parallelo non ritorna mai sui suoi passi;
una formica che cammina senza svoltare su un cono di plastica arriva sul bordo inferiore, così come camminando in montagna se non spingiamo di più col piede
che poggia in basso scendiamo di livello).
 |
|
|
|
|
Questi concetti dovranno essere ripresi e approfonditi nelle classi successive, nell'ottica di una ripresa a "spirale" degli argomenti, e tenendo conto che per gli stessi argomenti si possono prevedere diversi livelli di approfondimento: non si tratta di fare degli "anticipi", ma di utilizzare, in modi opportuni, terminologie e concetti che trovano naturali intrecci con altri concetti e di porre le basi per la costruzione di successivi livelli di formalizzazione. Ci pare fondamentale questo aspetto, sia per dare una immagine corretta e "viva" della matematica, sia per non favorire irrigidimenti mentali che identificano i concetti con particolari definizioni, particolari procedimenti di calcolo, … e li classificano in aree (la geometria, l'algebra, l'analisi, la probabilità, …) non comunicanti.
Una discussione più approfondita dell'impostazione dell'insegnamento geometrico, con una rapida storia della geometria stessa (e
vari esercizi per gli insegnanti), la trovi qui.
Abbiamo accennato, nel punto precedente, all'opportunità di introdurre, ad un primo livello, le funzioni circolari, indispensabili per affrontare sia le prime trasformazioni geometriche che le prime attività di area scientifica previste nelle altre discipline del biennio (in cui intervengono vettori, pendenze, …).
pendenza = 5/10 = 50%  |
 pendenza = ? / 1350 pendenza = tan(20*gradi) ? = tan(20*gradi)*1350 = 491 |
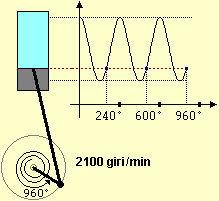 |
La prima delle figure precedenti ricorda la comparsa delle funzioni circolari nel momento che si valuta la pendenza di una strada, o di un grafico; la seconda il loro ruolo nel valutare l'altezza di un monte col goniometro verticale (riprendendo cose affrontabili nella scuola di base, e incominciando ad usare in modo opportuno la calcolatrice e il software). La terza figura visualizza operativamente il grafico di una funzione periodica di cui si può facilmente capire l'andamento (e di cui si potrà studiare l'espressione analitica solo nelle classi successive). Come già detto per altre voci, i concetti vanno introdotti gradualmente nel corso degli anni, intrecciandosi in modo naturale con altri temi. In questo caso lo studio delle funzioni circolari dovrà essere ripreso in tutti gli anni successivi della scuola superiore. Ovviamente, l'introduzione delle funzioni circolari precede lo "studio" (non l'uso) delle funzioni polinomiali, il quale richiede conoscenze tecniche e concettuali più avanzate.
Val la pena osservare che le funzioni circolari non vanno introdotte solo per gli angoli convessi, come poteva aver un senso un tempo (fino alla
metà del XX secolo), quando non esistevano le calcolatrici e quando la trigonometria era studiata essenzialmente per problemi topografici.
La funzione di inversa proporzionalità è una delle prime che si studiano nella scuola dell'obbligo, è di fondamentale importanza in tutta la matematica e in tutte le applicazioni di questa, e la sua ripresa deve, ovviamente, precedere l'introduzione delle funzioni polinomiali. Sicuramente nella scuola secondaria di 1º: grado saranno state affrontate situazioni come quelle illustrate nelle prime due figure, in cui viene messo in luce che, a parità di effetto, la forza esercitata e la lunghezza della traiettoria lungo cui la si esercita sono inversamente proporzionali. Anche l'idea di quanto di una vincita al totocalcio spetti a ciascun vincitore in funzione del numero di essi o (vedi il grafico a destra) di quanto costi mediamente in un mese una fotocopia (CU) fatta con una fotocopiatrice noleggiata mensilmente (dati il costo del noleggio e dati il costo incorporato, CI, della materie prime - carta e toner) in funzione del numero di fotocopie fatte, sono esempi in cui intervengono funzioni di inversa proporzionalità che potrebbero essere stati affrontati.
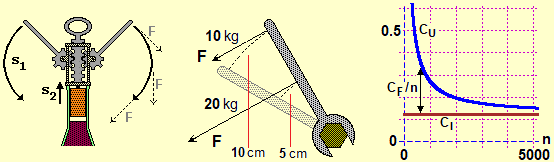
Nel primo biennio della scuola secondaria di 2º: grado a partire da esempi di questo tipo si deve arrivare allo studio delle funzioni
astratte
Abbiamo già osservato che un approccio costruttivista ai numeri reali è
indispensabile se si vogliono usare le radici quadrate (se no chi mi dice che esista la radice quadrata di 2?) o se si vogliono
considerare segmenti di lunghezza "esatta" (come un segmento lungo 5.010010001…), ossia un approccio in cui
• i numeri reali siano presentati come opportune successioni di caratteri (cifre, "." e "–"), con una opportuna
relazione di "eguaglianza" (3.7999… = 3.8000…, ecc.),
• le operazioni sui numeri decimali limitati siano definite algoritmicamente,
• e siano poi estese ai numeri reali mediante i concetti di approssimazione e, senza formalizzazioni, di limite e di funzione
continua (es.: per ottenere il risultato di x·y con una certa precisione basta operare su intervalli di indeterminazione per x e
per y sufficientemente piccoli).
A sua volta, le riflessioni, di approfondimento e di sintesi, sulla risoluzione (grafica, numerica e simbolica) delle equazioni non devono mirare a mettere a punto specifiche tecniche, quanto metodi basati sull'uso, più o meno formalizzato, di alcuni concetti generali: funzione inversa, funzione iniettiva e continuità.
A questo punto, già nel biennio (come suggerivano anche Villani e Spotorno [vedi]
nel lontano 1974), si può dare una prima sistemazione formale al concetto di continuità:
se una funzione è definita in un intervallo [a, b] e all'infittire degli input in tale intervallo fornisce output man mano più fitti,
allora si dice che tale funzione è continua in [a, b]. Si potrà, poi, dire che è continua in un qualunque insieme I di numeri reali se lo è
in ogni intervallo [a, b] contenuto in I (ad esempio
La figura seguente (in cui tracciamo il grafico per un numero via via maggiore di punti)
ci fa capire che la funzione
 |
Questa scelta, di introdurre la continuità (delle funzioni reali di variabile reale) su intervalli, non in
punti, è la scelta standard nell'ambito della matematica costruttiva ed è operata in vari manuali di Calculus americani. Essa,
oltre a facilitare poi l'introduzione dell'integrazione (altrimenti andrebbe dimostrato che la continuità puntuale implica quella su intervalli,
cosa non facile, e su cui sorvolano spesso i libri di testo, ricorrendo a dimostrazioni errate della integrabilità delle funzioni continue), ha due vantaggi:
• è più vicina al concetto "intuitivo" di continuità (che non è "puntuale") ed è adeguata a tutti gli sviluppi affrontabili nella scuola secondaria superiore;
• corrisponde al concetto di funzione tabulabile, ovvero di funzione F rappresentabile (graficamente o tabularmente) con un
calcolatore: comunque si fissi Δy si può trovare N tale che, ripartito [a,b] in N intervallini uguali,
Questo è un tipico esempio di una soluzione didattica che potrebbe superare alcune delle difficoltà
concettuali che gli alunni incontrano nell'affrontare l'argomento in questione.
Nell'ambito dello studio dei processi di apprendimento queste difficoltà vengono
spesso collegate alla presenza di alcuni "ostacoli epistemologici", che
si cerca di individuare sia con riflessioni "teoriche" che attraverso opportune
attività di sperimentazione. A volte, tuttavia, queste ricerche fanno
riferimento a una presentazione di un determinato concetto matematico (per
intenderci: la continuità definita puntualmente, gli enti geometrici primitivi
presentati per via assiomatica, ...) che viene assunta come assoluta, senza
preoccuparsi della possibilità di diverse presentazioni (spesso con clamorose
incomprensioni delle presentazioni matematiche scelte: si pensi alle confusioni
concettuali sull'aritmetica e la geometria presenti nei lavori di Piaget e,
soprattutto, dei suoi epigoni).
Per eventuali approfondimenti vedi QUI.
Sistemi di equazioni. Disequazioni
La risoluzione dei sistemi può essere naturalmente introdotta in collegamento con questioni di tipo geometrico: questo è il modo più efficace per avviare (e sviluppare in modo generale, e non meccanico) i principali argomenti e le principali attenzioni relative a quest'area della matematica.
 |
x2+y2=100 & x=6, x2+y2=100 & y=6, x2+y2=100 & y=x, x2+y2=100 & y=x2−12
Ma, ovviamente, moltissime situazioni affrontate sin dalla scuola di base dovrebbero aver già avviato a questa tematica, sia "geometricamente" che, soprattutto, in relazione a comuni situazioni problematiche, come la seguente (vedi qui):
 Luigi - 30 € |
 Maria - 44 € |
E l'uso del software di geometria dinamica, che individua "automaticamente" i punti di intersezione ad esempio tra un segmento e un cerchio, può porre il problema: come fa il programma a determinarne le coordinate (per poi tracciarli)?
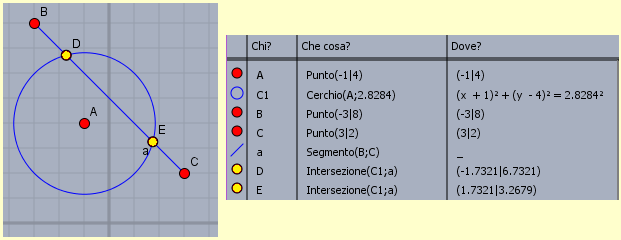 |
Dopo aver messo a fuoco in generale la tematica, ci si può soffermare sui sistemi lineari, mettendone in luce le caratteristiche
relativamente al numero di soluzioni. È da evitare accuratamente l'introduzione di trucchi strani (e quasi mai efficienti), come la "regola di Cramer".
È bene, invece, educare ad alcuni aspetti essenziali: • in assenza di parametri, se l'incognita è una coppia di variabili, ricorrere a metodi
grafici stimare le soluzioni, • prima di mettersi a fare manipolazioni, vedere se ci sono modi più semplici per individuare direttamente le soluzioni,
• verificare le soluzioni trovate, …
La riflessione sulle differenze rispetto agli altri sistemi di equazioni può essere evidenziata anche riflettendo sulla possibilità di risolvere
i sistemi lineari in modo "meccanico", usando del software. Qui, ad esempio, l'uso di un semplice script per il caso
di due equazioni:

e di questo per il caso di tre equazioni (e di questo per il caso di quattro equazioni):

Solo nelle classi finali delle superiori, e in alcuni tipi di scuole, ci si potrà poi soffermare sul concetto di determinante (vedi) e si potrà inquadrare il problema nell'ambito del calcolo matriciale.
Come già osservato per le voci precedenti, prima di fare esercizi senza un contesto di riferimento, è bene considerare situazioni problematiche, come ad esempio quella illustrata sotto a sinistra: dai grafici dei costi e dei ricavi relativi ad una particolare produzione, ricavare quando si è in pareggio, o quando il guadagno è "positivo". Questo è anche un esempio semplice di risoluzione di una disequazione. Mettere a fuoco, con esempi semplici ma significativi, i concetti e il loro uso, è un aspetto essenziale, molto più importante di quello di preparare dei provetti utilizzatori di formulette o procedimenti meccanici (finché ci se li ricorda!).
|
|
Così come si è detto per i sistemi, il concetto di disequazione va considerato in modo generale, come del resto si presenta in molte
situazioni concrete (per quali x
Abbiamo visto che uno dei primi concetti da riprendere e approfondire è quello di funzione, sotto forma sia di algoritmo che di tabella e di grafico, e che il riferimento a questo concetto entra in gioco nella definizione dei termini e, quindi, delle formule.
Abbiamo pure visto che le riflessioni, di approfondimento e di sintesi, sulla risoluzione
(grafica, numerica e simbolica) di equazioni, sistemi e disequazioni è opportuno che siano volte non tanto
alla messa a punto di specifiche tecniche, quanto alla individuazione di metodi basati sull'uso di alcuni concetti generali (funzione
inversa, funzione iniettiva, continuità, connettivi logici,
Sin dall'inizio è bene esaminare vari tipi di funzioni (e di equazioni), anche se poi ne vengono studiate più a fondo solo alcune (senza questo inquadramento più generale non si potrebbero mettere in luce, per contrasto, le caratteristiche di queste ultime). Abbiamo osservato che sono da evitare l'introduzione di tecniche ad hoc per questioni che possono essere affrontate con metodi più generali e lo sviluppo su casi particolari di aspetti che, senza dispendio e con maggiore significatività, possono essere visti in contesti più generali.
Con questa premessa, che in qualche modo riprende quanto osservato sui concetti di funzione e di risoluzione di un'equazione,
si vuole sottolineare l'importanza di avviare solo in un secondo tempo, verso la fine del primo biennio, lo studio delle equazioni polinomiali.
Per altro queste, e i polinomi più in generale, sono introdotti
in modi buffi, ed errati, in gran parte dei libri di testo (si vedano, ad esempio, quanto osservato qui).
Purtroppo le modalità in cui, spesso, vengono introdotti i polinomi nella scuola
secondaria superiore lasciano una traccia che dura nel tempo, anche in chi prosegue gli studi,
sia tra coloro che si iscrivono alle facoltà scientifiche (si vedano gli esiti di questo esercizio),
sia tra quelli che si laureano in esse (si vedano gli esiti di questo altro esercizio).
Ecco, secondo noi, sinteticamente, gli argomenti relativi alle funzioni polinomiali che (tra la fine del secondo anno e l'inizio del terzo) andrebbero affrontati:
• le funzioni polinomiali F hanno la caratteristica di avere un andamento del grafico
e il valore delle soluzioni di
•
le funzioni polinomiali sono tutte continue su R;
• tra i polinomi esiste un'operazione di divisione con resto, che ha varie analogie con quella tra i numeri interi;
• il teorema del resto (o di Ruffini);
• una equazione polinomiale di grado n ha al più n soluzioni;
• la soluzione di una equazione polinomiale di 2º: grado è interpretabile come ricerca
delle intersezioni con l'asse x di una parabola le cui coordinate dipendono dai coefficienti dell'equazione stessa;
• è utile memorizzare la scomposizione di alcuni polinomi in polinomi di grado inferiore.
Messi a fuoco il teorema del resto e il legame tra grado di un'equazione polinomiale e numero massimo delle soluzioni, si può ricorrere (come abbiamo visto considerando le equazioni) al software per rappresentare graficamente le funzioni e ad altro software (ad esempio WolframAlpha) per risolvere qualsiasi equazione polinomiale: non è affatto il caso di mettere a fuoco tecniche per risolvere equazioni polinomiali di grado superiore al secondo, se non quelle che possono essere studiate ricorrendo a delle semplici scomposizioni. Un esempio:
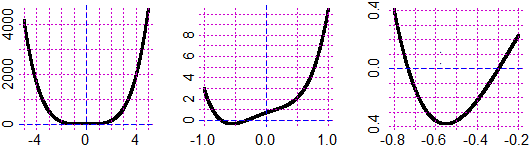 solve 7*x^4+sqrt(3)*x^3-x^2+2*x+2/3 for x real -0.29422093345889… -0.732580963760389… |
Poi, alla fine delle scuole superiori, si vedrà l'importanza che hanno le funzioni polinomiali in quanto consentono di approssimare, intorno a punti particolari, molti altri tipi di funzioni, più difficili da maneggiare (approssimazioni con polinomi di primo o secondo grado e, in alcuni tipi di scuole, i polinomi, e le serie, di Taylor).
Val la pena soffermarsi un attimo sulla cosiddetta regola di Ruffini,
da non confondere con l'importante "teorema di Ruffini":
è un procedimento "magico", che oscura il significato della divisione tra polinomi, di cui è facile perdere
il controllo semantico, che funziona solo in alcuni casi di divisione,
e che non fa risparmiare un gran ché né in termini di spazio né in termini di tempo. Data
la sua natura didatticamente dannosa, riportiamo qui
le considerazioni su di essa svolte da Vinicio Villani in un capitolo di un suo bellissimo
libro (che ogni insegnante dovrebbe leggere). [nota: all'estero è nota in genere come
"regola di Horner" (vedi: http://en.wikipedia.org/wiki/Horner's_method); Horner
e Ruffini hanno messo a punto questo metodo entrambi intorno al 1810, anche se esso era già stato
individuato più di 500 anni prima dal cinese Chu Shih-Chieh; la "regola" ha alcune applicazioni specifiche
che danno ad essa un ruolo ben diverso da quello esercitato dalle pratiche didattiche; all'estero
in genere non c'è alcuna traccia di questa regola nei libri di testo; vedi
qui quanto è dedicato alla divisione tra polinomi nell'eserciziario
di algebra che per decenni è stato il più diffuso al mondo]
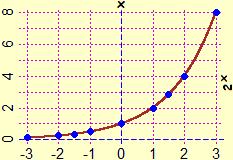 |
A lato è tracciato il grafico della funzione |
|
21.5 = 215/10 = 23/2 = (23)1/2 = √8 = 2.82842… 2−1.5 = 2−3/2 = 1/23/2 = 1/√8 = 0.353553… | |
|
Con un mezzo di calcolo ottengo valori anche
per altri esponenti; per 2π con WolframAlpha ho ad esempio: 8.82497782707628762385642960420800158170441081527148… Ricordiamo come potrebbe essere svolto il calcolo in questi casi: |
| π = 3.1415926535897932384626433832795028841971693993751… | ||
| 23 = 8 | ≤ 2π ≤ | 24 = 16 |
| 23.1 = 10√(231) = 8.5741877002… | ≤ 2π ≤ | 23.2 = 10√(232) = 9.1895868399… |
| 23.14 = 50√(2157) = 8.8152409270… | ≤ 2π ≤ | 23.15 = 20√(263) = 8.8765557765… |
| ... | ... | ... |
| 23.141592 = 8.8249738290… | ≤ 2π ≤ | 23.141593 = 8.8249799460… |
| ... | ... | ... |
Quello che abbiamo visto ora è il modo in cui è definita la funzione x → 2x:
per x razionale è definita nel modo illustrato all'inizio di questa voce, negli altri casi
è definta come abbiamo ora visto, in modo da essere continua, ossia in modo che all'infittire degli
input infittiscano gli output.
Se non si ha la necessità di introdurre la funzione esponenziale nel primo biennio, essa può essere
introdotta, in modo simile, al terzo anno. Nei libri di testo, spesso, la funzione esponenziale
viene usata brutalmente, senza averla definita se non per gli input interi!
Discutendo del concetto di numero reale abbiamo visto come si possa affrontare, nel primo biennio, una prima riflessione
sulle diversità "algebriche" delle diverse strutture numeriche, intese come sottostrutture di R.
Una volta introdotti altri oggetti matematici e modi di opeare con essi (funzioni, insiemi, vettori, trasformazioni geometriche, …) si possono,
alla fine del biennio o all'inizio del triennio, presentare, brevemente, alcune delle varie analogie (e differenze) strutturali tra i numeri e questi oggetti.
L'obiettivo non è quello di aggiungere altre nozioni, quanto quello di mettere a fuoco
collegamenti, somiglianze e diversità, sia per contribuire al formarsi di un'idea dei
legami più o meno espliciti che vi sono tra le varie aree della matematica,
sia per favorire il transfert (e l'unificazione) da parte degli alunni di idee, metodi, concetti
tra settori diversi. Si tratta di realizzare una sintesi di aspetti che dovrebbero essere stati messi in luce via via nell'insegnamento,
con livelli diversi di approfondimento a seconda del tipo di scuola e di classe. Gli oggetti matematici considerati non sono del tutto nuovi
rispetto ai livelli scolastici precedenti; quello che è nuovo è il sintetizzarli e unificarli facendo riferimento a idee più generali.
| g+f f+g f(g(.)) g(f(.)) "ca"+"sa" "sa"+"ca" not(P and Q) (not P) or (not Q) | ||
| Traslo di passi 2 ed 1 e ruoto attorno a 0 di −90º: Ruoto attorno a 0 di −90º: e traslo di passi 2 ed 1 |
| |
All'algebra "moderna", che affronta specificamente questi collegamenti, deve essere fatto qualche cenno.
L'obiettivo non è quello di fare di quest'area della matematica un oggetto
specifico di approfondimento (che potrà essere affrontato da parte di chi proseguirà
gli studi in ambito scientifico), ma è quello di contribuire al formarsi di un'idea unitaria della
matematica. Alcuni di questi obiettivi potranno essere ripresi e approfonditi negli ultimi anni delle scuole superiori.
Nelle scuole con taglio più professionalizzante questi aspetti saranno ovviamente affrontati in modo più operativo.
| Quante sono le possibili mani di poker? | y(0) = 1, y(n+1) = (y(n) + A/y(n)) / 2, y(n) → ? |
| Un biologo deve fare un esperimento su 60 topi, scelti tra i 100 di cui dispone. In quanti modi può effettuare la scelta? |
Verifica col computer che per n intero positivo 1³ + 2³ + 3³ +…+ n³ = (n·(n+1) / 2)² (vedi) |
 | (script) |
Un concetto importante da mettere a fuoco (anche per le varie applicazioni che troverà nelle classi successive) è quello di definizione per ricorsione, ossia della definizione di una funzione F (o di altri oggetti matematici) mediante uguaglianze in cui F compare sia a primo che a secondo membro. Tra le funzioni includiamo le successioni, che non sono altro che funzioni aventi per input i numeri naturali (tutti o quelli a partire da 1 o da un altro numero naturale), che possono essere indicate con la usuale notazione funzionale (a(1), a(2), a(3), …, come viene fatto in molti manuali di analisi matematica), o racchiudendo l'input tra parentesi quadre (a[1], a[2], a[3], …) o usando le scritture a1, a2, a3, …
 | (clicca QUI) |
Le definizioni ricorsive vengono poi usate per individuare diversi concetti di Calcolo combinatorio.
Quest'ultima è un'area della matematica ricca di applicazioni,
con molti agganci con altri settori, puri e non (analisi, algebra, calcolo delle probabilità, …),
che richiede buone, ma semplici, capacità di modellizzazione di
fenomeni di vario genere, e che non può e non deve essere banalizzata,
come purtroppo accade quasi sempre, nelle soluzione di qualche esercizio stereotipato.
È fondamentale non far imparare formulette a memoria, ma insegnare a ricavarle e
adattarle: gran parte dei problemi di tipo combinatorio non sono affrontabili usando direttamente qualche
procedimento risolutivo standardizzato, ma ricorrendo a forme di ragionamento ad hoc, semplici ma significative,
per cui è fondamentale la comprensione (e la rappresentazione matematica, in forme
diverse, che possono variare a seconda dei "gusti" delle persone) del problema da affrontare.
Affrontando la statistica descrittiva dovrebbero essere già stati introdotti i concetti e le tecniche di base per la rappresentazione e lo studio delle variabili casuali. Affrontando il calcolo delle probabilità si effettua il passaggio al caso in cui si fanno delle "previsioni", sulla base di considerazioni statistiche, di convinzioni o di informazioni di vario genere. Il calcolo combinatorio, ora considerato, offre alcuni strumenti per effettuare queste previsioni, in alcuni casi particolari.
| Il tema della probabilità dovrebbe essere già stato affrontato nelle scuole precedenti, ma spesso ciò non accade, o accade in modi "dannosi": si pensi ai molti libri in cui si "definisce" la probabilità come rapporto casi favorevoli/casi possibili, dimostrando l'ignoranza dei più elementari concetti matematici, e favorendo, nei ragazzi, lo sviluppo di misconcezioni che poi sarà difficile smontare (sul concetto di definizione vedi QUI). Il tema della probabilità, pur coinvolgendo, in prima battuta, concetti matematici molto elementari, è difficile da affrontare perché richiede una comprensione profonda delle situazioni da matematizzare, non una banale applicazione di qualche formuletta. Per questo motivo (e tenendo conto di come spesso viene affrontato nei livelli scolastici precedenti) il tema è da riprendere totalmente, facendolo precedere da riflessioni statistiche, e considerando situazioni varie, molte delle quali non sono affrontabili con lo schema "casi/casi" accennato sopra, come ad esempio quella illustrata qui a destra (un dado costruito col cartoncino). |
|
Del concetto di probabilità occorre precisare le regole a cui deve sottostare, esplicitando che la scelta dei valori di probabilità da assegnare non dipende,
in prima battuta, da considerazioni matematiche, ma da esperimenti, idee, supposizioni, … nelle quali la matematica non ha un ruolo di guida. In pratica
è una definizione assiomatica (quella richiamata nella figura seguente, in cui A1, A2,
A3, … sono eventi incompatibili), come varie altre che gli alunni hanno incontrato nei lori studi,
anche se non sono state chiamate in tal modo (gran parte della aritmetica, per esempio, viene appresa "assiomaticamente";
anche il concetto di distanza, euclidea o urbanistica, viene definito in questo modo). Questo è il primo contesto in cui è chiaro e significativo
esplicitare questo aspetto: è "ovvio" che se ritengo che con la probabilità del 50% l'Inter batterà il Milan e che al 20% le due squadre pareggeranno,
per me al
 |
Oltre a situazioni, come quella dell'esempio precedente (Inter-Milan), in cui le valutazioni probabilistiche sono soggettive, o quella del dado non equo, in cui possono essere effettuate dopo aver assegnato probabilità di uscita alla varie facce dopo degli esperimenti, vi sono anche situazioni in cui le uscite sono infinite, come nell'esempio seguente. Ecco perché i "..." nella figura soprastante.
|
Lancio N volte una moneta equa fino ad ottenere "testa". A volte basta N = 1, a volte N = 2, a volte N = 3, ..., ma potrebbero essere necessari una quantità innumerevole di tentativi. Qual è la probabilità che basti N = 1? E che basti N =2? ... |
Vi sono, poi, situazioni semplici di cui non è facile trovare la soluzione teoricamente, o in cui la si vuole verificare per esserne certi. In queste casi può essere utile ricorrere al computer, per simulare il fenomeno con il generatore di numeri casuali e studiarlo con strumenti statistici. Un esempio, per chiarire questo aspetto:
| Qual è la probabilità che lanciando due dadi equilibrati la differenza delle uscite sia 1? Sperimentalmente: Event = function() abs( RUNIF(1, 1,6)-RUNIF(1, 1,6) ) == 1
PR = function(n) {f=0; for (i in 1:n) f = f + ifelse(Event(),1,0); f/n*100}
PR(1e4); PR(1e5); PR(1e6)
# 28.17 27.607 27.7118Teoricamente:le uscite buone sono 12, 23, 34, 45, 56, 65, 54, 43, 32, 21, e 10/36 = 5/18 = 27.777… |
Gli strumenti che intervengono per matematizzare le situazioni di incertezza sono, come abbiamo visto, in gran parte gli stessi che si impiegano nelle altre aree della matematica. I grafi ad albero e le tabelle di ripartizione percentuale sono particolarmente utili per affrontare un altro concetto che deve essere messo a fuoco nel primo biennio: quello della dipendenza/indipendenza di eventi e di variabili casuali:
|
Qual è la probabilità che alzando 2 volte un mazzo di carte da scopa ottenga sempre una carta di denari? |
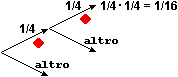 |
Qual è la probabilità che estraendo 2 carte dal mazzo queste siano entrambe di denari? |
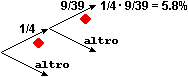 |
Molti degli esempi affrontabili fanno riferimento al gioco, un po' per la natura stessa dei concetti probabilistici, un po' perché si tratta di situazioni più facilmente modellizzabili, in cui è più agevole estrarre gli aspetti significativi. Ma è bene riferirsi anche a contesti non di gioco, ad esempio a situazioni in cui, in base a valutazioni probabilistiche si devono fare delle scelte in una attività produttiva o in un contesto giudiziario, o in cui si devono fare delle valutazioni di natura biologica o sanitaria. Basti pensare alla genetica o al contesto messo in luce dal seguente esempio, o a quello messo in luce da quest'altro.
|
Un certo test sanitario per valutare la presenza (esito positivo) o assenza (esito negativo)
La probabilità è 0.95% / 5.90% = 16%, molto meno di 95%, come si sarebbe potuto pensare. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Il fatto che gli strumenti probabilistici siano da utilizzare (e i cui esiti siano da interpretare) in contesti non puramente matematici è forse il motivo per cui essi sono spesso trascurati dai docenti o sviluppati in modi del tutto scorretti. È invece essenziale, dal punto di vista educativo, affrontare questa tematica, cercando anche di mettere in luce le difficoltà e gli errori che gli alunni possono commettere affrontando questioni probabilistiche. Questo è un aspetto decisivo per quest'area della matematica, per le questioni affrontate sopra, e per favorire lo sviluppo di attenzioni verso le sciocchezze, anche gravi, che i mass media vari spesso propongono facendo riferimento a valutazioni probabilistiche.
Quest'area della matematica è forse quella che, rispetto alle altre da affrontare nel primo biennio, richiede uno sviluppo più strutturato, aprendo anche ad un modo più organico di svolgere i temi che dovrebbe caratterizzare gli anni successivi. Nel secondo biennio le aree della statistica e della probabilità troveranno un più forte intreccio quando verrà messo a fuoco il teorema limite centrale, di cui, tuttavia, l'idea che, in un esperimento statistico, all'aumentare delle prove il rapporto tra numero delle uscite favorevoli e totale delle uscite tenda a stabilizzarsi sulla probabilità costituisce una qualche forma di anticipazione. Qui si possono trovare considerazioni culturali, didattiche e tecniche che approfondiscono alcuni aspetti. Qui si può trovare una breve storia del calcolo delle probabilità.
Il generatore di numeri casuali (di cui abbiamo parlato più volte) viene spesso chiamato generatore di numeri pseudocasuali in quanto i numeri sono prodotti da un programma che li genera secondo un certo algoritmo con distribuzione che è "praticamente" uniforme. Scegliendo un particolare valore (detto "seme") si può far sì che venga generata una particolare sequenza. Per approfondimenti vedi QUI. Esso può essere usato anche per codificare e decodificare ("segretamente") testi; vedi QUI.
Usando il software R è possibile riordinare facilmente i numero d'ordine dei quiz in un compito in classe. L'insegnante sceglie il seme, ad esempio 120, e riordina i quesiti (ad esempio 15) per i suoi 30 alunni con i comandi - preceduti da source("http://macosa.dima.unige.it/r.R") - seguenti:
| set.seed(120+1); sample(15) | ottenendo: | 4 12 14 7 15 9 1 3 8 5 11 10 2 13 6 |
| set.seed(120+2); sample(15) | 8 9 10 12 7 14 2 4 3 13 11 15 1 6 5 | |
| ... | ||
| set.seed(120+30); sample(15) | 3 14 15 1 13 4 5 7 8 9 11 12 2 10 6 | |
| ovvero se i quesiti sono indicati con lettere: | ||
| set.seed(120+1); SAMPLE(15) | D L N G O I A C H E K J B M F | |
| set.seed(120+2); SAMPLE(15) | H I J L G N B D C M K O A F E | |
| ... | ||
| set.seed(120+30); SAMPLE(15) | C N O A M D E G H I K L B J F | |
Oppure, se i quesiti sono a risposta chiusa, con ad es. con 5 e 4 risposte, si possono riordinare le risposte possibili:
set.seed(120+1); sample(5); set.seed(120+1); sample(4) 4 5 3 2 1 4 3 2 1
set.seed(120+2); sample(5); set.seed(120+2); sample(4) 1 2 3 5 4 4 1 2 3
...
Diversificazioni didattiche
Quelli che abbiamo indicato sono gli argomenti che potrebbero essere affrontati nel primo biennio della scuola superiore,
tenendo conto che il livello di approfondimento può essere diverso a seconda del tipo di scuola, ed anche delle caratteristiche delle singole classi.
Al primo anno esistono alunni con diverse "capacità", non facili da esplorare: spesso la scuola oscura o sopravvaluta le abilità e
le potenzialità dei vari alunni, mentre le prime settimane di scuola dovrebbero essere volte ad indagare, non fiscalmente, con attività di vario genere, i loro stili
cognitivi, le loro conoscenze, le loro misconcezioni, … All'inizio del secondo anno si dovrebbe affrontare con analoghe attenzioni l'eventuale arrivo di nuovi alunni.
In molte voci abbiamo visto come il software possa essere impiegato per facilitare la gestione didattica di molti contenuti, consentendo di affrontare
gli stessi temi con livelli diversi di approfondimento tecnico in realtà scolastiche differenti. E, al di là dell'uso del software, bisogna individuare
i contenuti e i metodi matematici essenziali da affrontare in ogni contesto, intrecciandoli alle altre aree disciplinari, in modo diverso, ad esempio, in una
scuola ad indirizzo artistico rispetto ad una con indirizzo scientifico o tecnico o classico o commerciale. Ed occorre che, in una stessa classe,
i temi siano affrontati in modo che tutti possano seguire il "filo del discorso" e comprendere gli aspetti essenziali dei concetti matematici introdotti,
tenendo conto che, nella ripresa a spirale degli stessi che deve caratterizzare l'insegnamento nei successivi anni, gli alunni potranno consolidarne
in tempi differenti la padronanza.
E occorre tener conto che il rinnovamento continuo della matematica, dei suoi usi, delle sue interazioni con le altre discipline,
delle tecnologie disponibili, delle opportunità offerte dalla rete richiedono che buona parte dei contenuti e delle tecniche, divenute obsolete,
siano via via ridimensionate o "buttate a mare" per dare spazio a nuovi contenuti e nuove tecniche, e ad atteggiamenti che consentano di reperire,
selezionare ed usare quanto i nuovi media propongono. La matematica è viva.