INDICE

Su alcuni concetti / temi matematici da affrontare negli ultimi anni delle superiori
("intrecciati" all'interno di unità didattiche)

[scuola  primaria - A   primaria - B   sec. 1º grado   sec. 2º grado - A   sec. 2º grado - B]

Il concetto di modello
I numeri reali (e quelli complessi)
Altre basi di numerazione
Il concetto di limite
Continuità, integrazione, derivazione, antiderivazione
Funzioni esponenziale e logaritmo
Lo spazio
La statistica e il calcolo delle probabilità
Relazioni tra due variabili casuali
Approfondimenti di analisi matematica
Altro
Diversificazioni didattiche, e considerazioni conclusive 

Negli ultimi anni delle superiori, oltre ad essere approfonditi temi già presenti nei livelli scolastici precedenti, sono avviati nuovi temi (il calcolo differenziale e integrale, ma non solo).
Essi sono presentati articolati per aree diverse ma, come via via chiarito, nei percorsi didattici i diversi concetti matematici devono intrecciarsi tra di loro e con le altre discipline.
Alcuni dei temi presentati nella parte relativa ai primi anni delle superiori, anche se qui non sono richiamati, devono essere ripresi e sviluppati in questi anni finali.
Nell'ultimo paragrafo sono presenti indicazioni sulle possibili diversificazioni dello sviluppo didattico nei vari tipi di scuole.
Esempi di impiego di gif animati, utili per introdurre in modo più intuitivo nei diversi livelli scolastici vari temi, sono presenti QUI.

Il concetto di modello

    La matematica può essere definita la scienza dei modelli. Il concetto di modello deve dunque avere un ruolo centrale nel suo insegnamento sin dai primi livelli.

    Per un approfondimento di questi aspetti rinviamo al documento relativo ai primi anni delle scuole superiori.
 

I numeri reali (e quelli complessi)

    La padronanza della rappresentazione decimale dei numeri dovrebbe essere uno degli obiettivi dell'insegnamento nella scuola media inferiore. È essenziale che all'inizio delle superiori siano state impostate attività didattiche che abbiano consentito di verificare questa padronanza ed eventualmente avviare delle attività che l'abbiano consolidata.  Su questo aspetto ci siamo soffermati nel documento relativo ai primi anni delle scuole superiori.  Un atteggiamento analogo dovrebbe essere tenuto per gli eventuali nuovi alunni che si inseriscono nelle ultime classi delle superiori.
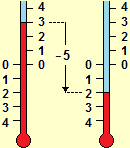
    Richiamiamo solo l'immagine "sintesi" seguente ed alcune considerazioni.

   

    Per una corretta e significativa introduzione dei numeri è opportuno scegliere un approccio costruttivista; in breve:
–  numeri reali come opportune successioni di caratteri (cifre, "." e "–"), con una opportuna relazione di "eguaglianza" (3.7999…=3.8000…, ecc.),
–  definizione algoritmica delle operazioni sui numeri decimali limitati,
–  estensione di queste ai numeri reali mediante i concetti di approssimazione e, senza formalizzazioni, di limite/funzione continua (es.: per ottenere il risultato di x·y con una certa precisione basta operare su intervalli di indeterminazione per x e per y sufficientemente piccoli).
    I numeri naturali, interi, periodici/razionali, decimali limitati e limitati in altre basi vengono studiati come particolari sottoinsiemi di R chiusi rispetto ad alcune operazioni. 
    Non è opportuno né, ovviamente, introdurre i numeri reali per via assiomatica, né presentare la costruzione dei vari insiemi numerici a partire da N:
–  sarebbe dispendioso e difficile introdurre gli strumenti algebrico-logico-insiemistici per effettuare "correttamente" la costruzione (anche il solo passaggio) agli interi
–  e, soprattutto, a questo livello, non se ne vedono motivazioni "didattiche" (in un corso universitario di algebra la costruzione di Q a partire da N può essere invece un'occasione di applicazione di concetti come partizione, immersione, …) o "culturali" (in un corso universitario sui fondamenti della matematica può essere invece significativo costruire con tecniche insiemistiche a partire dall'aritmetica di Peano un modello per gli assiomi dei numeri reali).

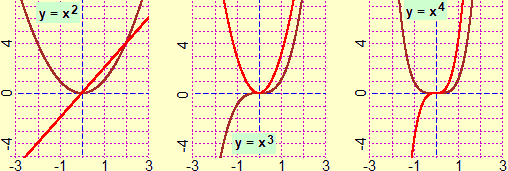
    Quelli ora richiamati sono concetti e metodi che devono essere introdotti negli anni precedenti e che devono essere ripresi negli ultimi anni, intrecciandosi a questioni qui discusse parlando di continuità, integrazione, derivazione.  Nella scuola superiore occorre accennare ad un altro concetto con cui sicuramente avrà a che fare chi svolgerà un mestiere che abbia a che fare con l'uso del computer (o con la tecnologia elettronica):  i numeri complessi.  Partiamo da un esempio.

    Se con WolframAlpha risolvo l'equazione polinomiale  2/3 + 2 x − x2 + √3 x3 + 7 x4 = 0  ottengo:

solve 2/3 + 2*x - x^2 + sqrt(3)*x^3 + 7*x^4 for x
−0.294221   −0.732581   0.389683−0.53852i   0.389683+0.53852i

    Per ottenere solo le soluzioni reali devo aggiungere:

solve 2/3 + 2*x - x^2 + sqrt(3)*x^3 + 7*x^4 for x real

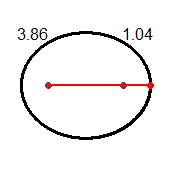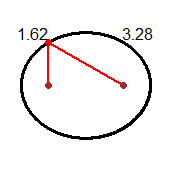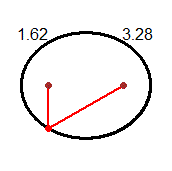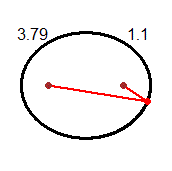
    A questo punto sorge spontanea la domanda del perché vengano visualizzati questi strani numeri? A che cosa servono?  Una prima risposta, affrontabile con tutti gli alunni, è richiamata nella prima delle figure seguenti:  i numeri complessi costituiscono un modo alternativo per descrivere i vettori e i punti del piano (ad esempio la somma di due numeri complessi equivale alla somma dei corrispondenti vettori).  Una seconda risposta, affrontabile anche questa con tutti gli alunni (se si ha tempo a disposizione), è quella richiamata dalla seconda figura: con i numeri complessi si possono descrivere facilmente molte trasformazioni geometriche, in questo caso quella che ruota attorno a (0,0) di atan(3/4) e dilata del fattore √(4²+3²).

   
Numeri complessi per rappresentare punti del piano e vettori.  La trasformazione geometrica  z → z·(4+3i).
La trasformazione geometrica  (che conserva gli angoli di incidenza)  T: z → 3/(z+1)+z−4i

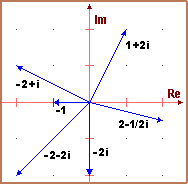
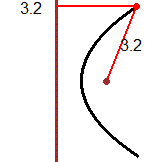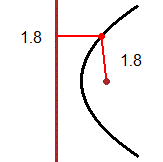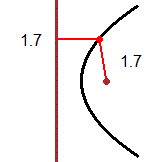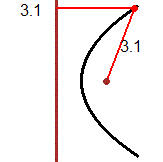
    Nei licei scientifici e negli istituti tecnici industriali si possono studiare anche le trasformazioni conformi, come quella rappresentata nella terza figura.  Per approfondire questi aspetti, in una possibile scheda di lavoro per gli studenti, vedi qui.  Nel paragrafo 6 di essa trovi anche qualche riflessione storica sulla "strana" origine dei numeri complessi (come trucco per risolvere alcune equazioni polinomiali), affrontabile eventualmente nei licei.
 

Altre basi di numerazione

    Con questa calcolatrice se eseguo  843.27−843.23  e  5555ᱹ1251 − 5555  ottengo  0.03999999999996362  e  0.12510000000020227  invece che  0.04  e  0.1251.  Come mai questi risultati diversi da quelli ottenuti con una usuale calcolatrice tascabile?

    Provo ad eseguirli con un foglio di calcolo.  Esamino che cosa si ottiene nel primo caso (vedi la figura seguente).  Sembra di ottenere in C1 (dove ho messo "=A1−B1") il risultato atteso (0.04), ma se faccio la differenza tra il risultato ottenuto e 0.04 non ottengo 0!  Se calcolassi la differenza tra i due valori (0.04−3.63806e-14) otterrei 0.03999999999996362, valore analogo a quello ottenuto con la precedente calcolatrice.  Nel caso dei fogli di calcolo  (a differenza di altre applicazioni gratuite, ma più affidabili, come R)  è meno facile esplorare questi fatti  (occorre districarsi in un menu fatto apposta per avere begli effetti ma non banale per svolgere delle riflessioni non superficiali; sono stati diversi i problemi finanziari che alcune banche hanno incontrato usando i fogli di calcolo: una piccola differenza, non vista, moltiplicata per grandi numeri, può dar luogo a valori molto grandi).

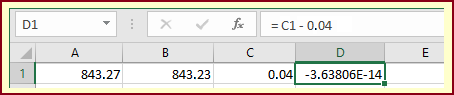
    Come mai accade ciò?
    A differenza di quanto avviene nelle usuali CT, che memorizzano i numeri in forma decimale (memorizzano in forma binaria solo le singole cifre), gran parte delle applicazioni per computer memorizzano i valori numerici nei registri associati alle variabili in forma binaria. Si può avere un'idea di come ciò accade con questa semplice applicazione.  Eccone due particolari uscite, per il calcolo del rapporto tra due interi espresso in forma decimale e in forma binaria:

Divisione di m per n con m < n (numeri naturali in base dieci) e risultato in base a scelta.
Cliccando  [Fai un passo]  ottieni via via le cifre del risultato
m = n = base =
resto =    

Divisione di m per n con m < n (numeri naturali in base dieci) e risultato in base a scelta.
Cliccando  [Fai un passo]  ottieni via via le cifre del risultato
m = n = base =
resto =    

    Il concetto di numero limitato (cioè numero con periodo 0) dipende dalla base di rappresentazione. 1/2, che in base dieci è 0.5, in base due diventa 0.1; ma 1/10, che in base dieci diventa 0.1, in base due diventa il numero illimitato 0.00011001100110011… in quanto non riesco ad esprimere 0.1 come somma di una quantità finita di frazioni prese tra 1/2, 1/4, 1/16, 1/32, ... (che, scritti in base due, diventano 0.1, 0.01, 0.001, 0.0001, …).   A questo punto ci è facile capire le uscite strane considerate all'inizio del paragrafo.  843.27 e 843.23 vengono internamente espressi in forma binaria e approssimati, viene fatta la differenza tra questi due numeri in base 2, e il risultato viene visualizzato in base dieci: 0.03999999999996362 è il risultato che differisce da 0.04 del valore decimale corrispondente alle cifre binarie che si sono perse.

    I programmi considerati riescono a rappresentare un numero finito di numeri. Avranno, quindi, anche un numero massimo.  Con la calcolatrice considerata all'inizio del paragrafo il massimo numero che riesco a calcolare è 21024 (1024 è pari a 2 alla 10, ossia, in base 2, a 10000000000); mi viene dato 1.797693e+308 come risultato; se aumento di 1 l'esponente o di 0.00001 la base mi viene segnalato un errore di overflow.

    Con gli alunni di tutti i tipi di scuole, al di là degli approfondimenti teorici, occorre mettere a fuoco, operativamente (facendogli fare calcoli, errori, confronti, …), il fatto che i mezzi di calcolo svolgono i calcoli non in forma decimale e che i numeri che appaiono visualizzati non è detto che corrispondano a quelli memorizzati internamente.
 

Il concetto di limite

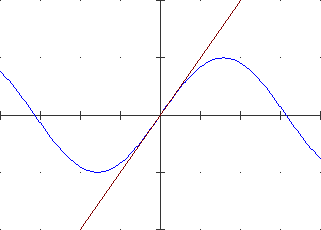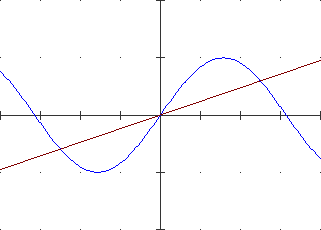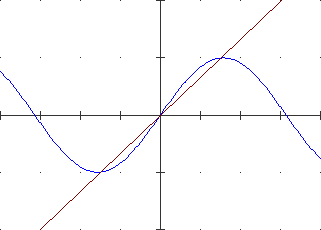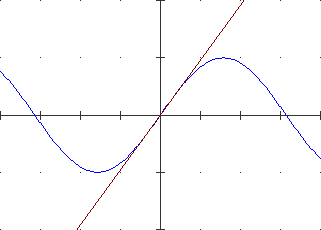
    La parola "limite" (e parole da essa derivate, come "limitato", "illimitato", …) viene usata molte volte in matematica. Ad esempio si dice che:
– l'intervallo [3, ∞) non ha limiti superiori,
– un punto che procede oltre ogni limite in una direzione fissata descrive una semiretta,
– un angolo è una figura illimitata (cioè che si estende senza limitazioni),
– un'espressione decimale illimitata prosegue dopo il "." con una sequenza infinita di cifre.
    In questi casi, come anche in molti contesti non matematici («a tutto c'è un limite», «se il livello dell'acqua del bacino scende sotto al limite di guardia scatta il razionamento dell'acqua», …), "limite" indica qualcosa che non può essere superato.
   In altre situazioni la parola limite viene usata con un significato un po' diverso:  «dopo l'apertura del paracadute ha incominciato a frenare, e la velocità di caduta si è progressivamente stabilizzata sul valore limite di 20 km/h», ….
    Si tratta di casi in cui stiamo considerando un certo processo che evolve verso una condizione limite; qui usiamo "limite" nel senso di uno stato che un certo fenomeno tende ad assumere.

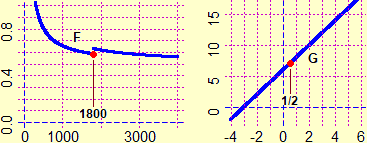
   La figura a destra dovrebbe chiarire la differenza tra i due usi. Se a una pallina di gomma immersa in un secchio d'acqua do una piccola spinta verso il basso la pallina incomincia a oscillare: il suo centro scende alla quota L1, poi sale alla quota L2, poi scende un po' meno, poi risale, …;  L1 e L2 sono un limite inferiore e uno superiore alla posizione che potrà assumere il centro della pallina;  al passare del tempo le oscillazioni si smorzano e il centro della pallina tende ad assumere la posizione limite L.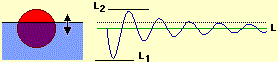   

    

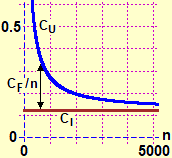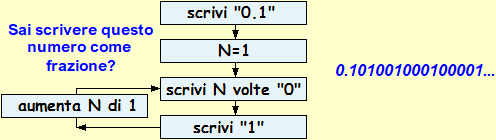
    In questo paragrafo ci soffermiamo sul secondo uso ("limite" come stato a cui tende un processo), che è quello più frequente in matematica, e che più o meno esplicitamente si dovrebbe essere già usato molte volte nelle classi precedenti:

•  Il numero 0.101001000100001…,  le approssimazioni per troncamento 2, 2.2, 2.23, 2.236, … di √5,  il numero periodico 3.777…  indicano le espressioni "limite" a cui tendono questi processi di scrittura, che non potremo mai completare.

•  Nel caso del noleggio di una fotocopiatrice il costo unitario di una fotocopia tende a coincidere col costo incorporato di carta e toner in quanto, all'aumento del numero delle copie fatte, i costi fissi tendono ad ammortizzarsi (vedi il grafico a lato).

•  Lanciando ripetutamente una moneta (equa) la frequenza relativa con cui esce "testa" tende a stabilizzarsi su 0.5.

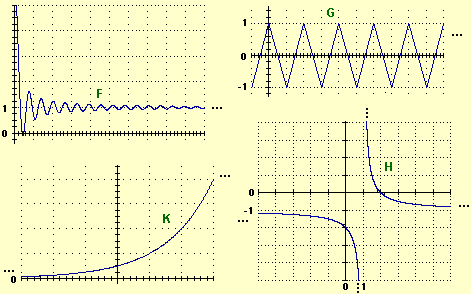
    Piuttosto che "definire formalmente" il concetto di limite occorre porsi il problema di costruirne il significato. Ad esempio, restringendosi alle funzioni a 1 input e 1 output reali,  occorre imparare a descriverne, a partire dai grafici, particolari comportamenti usando il simbolo lim:

 lim  F(x)  = 1 
 x → ∞
lim  G(x)  non esiste
x → ∞
lim  K(x) = ∞
x → ∞
lim  K(x) = 0
x → –∞

lim  H(x) = –1
x → ∞
  lim  H(x) = –1   ; 
  x → –∞
lim  H(x) = –∞
x ↑ 1
lim  H(x) = ∞
x ↓ 1

    Si può poi far esprimere "a parole" il significato di limite.  Ad esempio, se l'input tende a K e il limite L è finito, posso dire: "avvicinando il valore dell'input a K posso far sì che l'output si stabilizzi vicino quanto voglio a L";  o, se L è ∞, posso dire: "avvicinando il valore dell'input a K posso far sì che l'output sia maggiore di qualunque valore abbia fissato".  E si può far riflettere  (ora o quando si affronterà il legame tra statistica e probabilità - vedi)  sul fatto che nel caso del lancio della moneta la frequenza relativa con cui esce "testa" tende a stabilizzarsi vicino ad 0.5, ma non con "certezza".

    Occorre mettere a fuoco alcuni aspetti importanti, come il seguente, che fa riferimento alle due figure a lato, in cui i pallini rossi indicano dei punti che non appartengono ai grafici.
    La funzione rappresentata nel primo grafico in 1800 assume un valore maggiore del limite a cui tende la funzione al tendere dell'input a 1800 "da sinistra".  Quando l'input passa per 1800 il grafico della funzione fa un salto.  È una funzione che è non è continua in 1800.
    Nel caso della seconda funzione, x → (2·x²+5·x−3) / (x−1/2)  (rapporto che vale 2x+6),  il grafico quando l'ascissa vale 1/2 ha un "buco".  La funzione comunque è continua nel suo dominio  (in molti libri di testo si trova invece che questa funzione sarebbe discontinua, costruendo un grave misconcetto nella testa degli alunni).  Se assegno a 1/2 il valore 2·1/2+6, cioè 7, posso "prolungare" la funzione in modo da ottenerne una continua in tutto l'insieme R.

    

    È poi facile mettere a fuoco, attraverso esempi e ragionamenti "grafici", che il passaggio al limite conserva somme, prodotti, quozienti e le relazioni d'ordine ≥ e ≤ .  Nel caso raffigurato sotto a sinistra abbiamo che il limite di sin(1/x)·x per x → 0 è 0 in quanto la funzione è compresa tra due altre funzioni che in 0 valgono 0.

    Con qualche semplice esempio grafico si può capire come estendere le proprietà considerate sopra ai casi in cui i limiti siano infiniti.  Ad esempio se F(x) → L e G(x) → ∞, F(x)+G(x) → ∞.  In breve:  L+∞ = ∞.  Analogamente:  ∞+∞ = ∞,  L/∞ = 0  e, se L > 0,  L·∞ = ∞.  Ma, come fa capire la figura soprastante a destra,  ∞−∞ = ?,   ∞·0 = ?,   ∞/∞ = ?

    Nei licei si può vedere come le proprietà relative al passaggio al limite di, ad esempio, una somma di funzioni possono essere tradotte in spiegazioni ("ε-δ") più formali.  Ma questo può essere fatto solo per dare agli alunni un'idea di come i ragionamenti potrebbero essere tradotti in procedimenti più rigorosi, non come argomentazioni che spieghino queste proprietà.

    I limiti delle successioni devono essere trattati come limiti di funzioni al tendere dell'input a ∞, non devono essere studiati come un argomento a sé stante!
 

Continuità, integrazione, derivazione, antiderivazione

    Nel documento relativo ai primi anni delle superiori abbiamo visto come, consolidato il concetto di funzione (vedi), sia opportuno già in questi anni scolastici dare una prima sistemazione formale al concetto di continuità (vedi):  se una funzione è definita in un intervallo  [a, b]  e all'infittire degli input in tale intervallo fornisce output man mano più fitti, allora si dice che tale funzione è continua in  [a, b].  Si dice che è continua in un qualunque insieme I di numeri reali se lo è in ogni intervallo [a, b] contenuto in I (ad esempio  x → 1/x  è continua in R−{0}).  Al terzo anno delle superiori questo concetto deve essere ripreso (e introdotto per gli eventuali nuovi alunni).
    Ad esempio si può considerare una funzione come  x → (20−2·x)²·x  e tracciarne il grafico per un numero via via maggiore di punti  per capire che essa è continua in [0, 10].

    Ricordiamo che questa scelta, di introdurre la continuità (delle funzioni reali di variabile reale) su intervalli, non in punti, ha diversi vantaggi:
•  è più vicina al concetto "intuitivo" di continuità (che non è "puntuale") ed è adeguata a tutti gli sviluppi affrontabili nella scuola secondaria superiore;
•  corrisponde al concetto di funzione tabulabile, ovvero rappresentabile (graficamente o tabularmente) con un calcolatore:  comunque si fissi Δy si può trovare N tale che, ripartito [a,b] in N intervallini uguali, f(x) è approssimata con errore inferiore a Δy da f(xi) se xi è un estremo dell'intervallino in cui cade x;
•  facilita l'introduzione dell'integrazione (altrimenti andrebbe dimostrato che la continuità puntuale implica quella su intervalli, cosa non facile, e su cui sorvolano spesso i libri di testo).

    Dopo aver introdotto come calcolare l'area di un qualunque poligono negli anni precedenti (ad esempio come unione di triangoli o come differenza di aree di trapezi), date, in ordine antiorario, le coordinate dei vertici, ora è facile introdurre il concetto di integrazione definita.  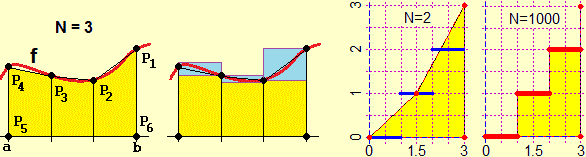L'area che sta tra il grafico di una funzione f e l'asse delle x, per x che varia tra a e b, posso approssimarla con l'area  areaF(f, a,b, 3)  del poligono P1P2…P6 ottenuto suddividendo [a,b] in 3 parti uguali, chiamando P1, P2, P3 e P4, in verso antiorario, i punti corrispondenti del grafico e chiamando P5 e P6 i punti dell'asse x di ascissa a e b.  Dato che all'infittire degli input infittiscono gli output, all'aumentare del numero N delle parti la striscia (celeste) al cui interno sta il grafico di f  (e che contiene la poligonale che approssima il grafico)  ha spessore che tende a 0.  Quindi l'area del poligono  areaF(f, a,b, N)  all'aumentare di N si stabilizza su un numero reale, che assumiamo come valore dell'area sottesa al grafico di f.

    La figura sopra a destra illustra il caso di una funzione "continua a tratti", ossia definita in un intervallo che è l'unione di intervallini in cui la funzione è continua e limitata.  Anche in questi casi il procedimento si stabilizza su un numero, che assumiamo come valore dell'area sottesa al grafico.

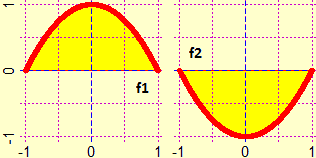         A lato sono rappresentati, al variare delle ascisse tra −1 ed 1, i grafici di f1 e f2.  Se implemento areaF(f, a,b, N) con un qualunque programma e lo uso per valutare le aree tra essi e l'asse x ottengo, rispettivamente, 4/3 e −4/3. Infatti il programma calcola le aree orientate: positive se stanno sopra all'asse x, negative se stanno sotto ad esso. Le "aree" delle due superfici sono invece entrambe positive  (qui puoi trovare una possibile implementazione del programma).
 areaF(f1,-1,1,2000);  areaF(f2,-1,1,2000)
 #  1.333333             -1.333333
    Senza scaricare un programma, possiamo calcolare facilmente integrali definiti (di molti tipi di funzioni) con questo script eseguibile online, qui usato per effettuare lo stesso calcolo (dell'integrale di x → −x^2+1 tra −1 ed 1) effettuato sopra:

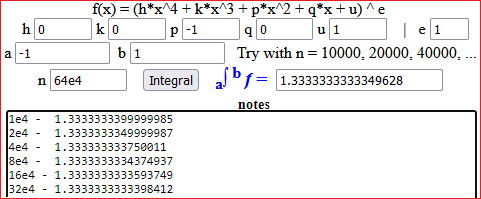
    È importante svolgere qualche calcolo approssimato di integrali definiti con del software per mettere a fuoco l'idea di integrazione, spesso oscurata dal concetto, diverso, di antiderivazione.

    A questo punto si può definire l'integrale di una qualunque funzione F che sia continua in un intervallo [a,b], o che sia ivi limitata e continua in un insieme finito di intervalli la cui unione sia [a,b].
    Si possono poi mettere a fuoco, facilmente, altre proprietà dell'integrazione:

∫ [a, b] (F+G)  =  ∫ [a, b] F  +  ∫ [a, b] G             ∫ [a, b] (k F)  =  k ∫ [a, b] F

    Il concetto di integrazione definita deve essere introdotto separatamente e prima di quello di integrazione indefinita (o antiderivazione), temi che, poi, dovranno essere messi in connessione dal teorema fondamentale dell'analisi, su cui ci soffermiamo fra un po'.
    Questo collegamento, e, ovviamente, il concetto di derivazione, devono essere introdotti, ad un primo livello, nella classe terza, in quanto indispensabili per le attività di matematizzazione dei fenomeni fisici, nonché per l'avvio del calcolo probabilistico nel caso continuo (per passare dagli istogrammi alle funzioni di densità - vedi la figura a lato - e mettere a fuoco il fatto che vi sono figure illimitate di area finita).

    Soffermiamoci, ora, sul concetto di derivazione.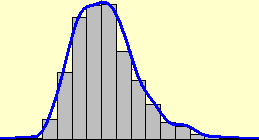

 

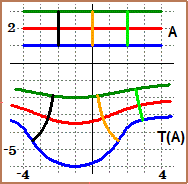
    Nella scuola secondaria di 1º grado, e nel primo biennio di quella di 2º grado, agli alunni è già stato introdotto il concetto di pendenza (o coefficiente direttivo) delle rette (vedi).  Nella classe terza si può riprendere il concetto a partire da situazioni concrete.  Ad esempio nel caso del grafico seguente si può chiedere agli alunni:
"in quale periodo in la temperatura è rimasta più o meno costante?  intorno a quale valore intero essa ha oscillato?  qual è stata la velocità media di variazione della temperatura (misurata in ºC all'ora) nell'intervallo di 6 ore in cui essa è cresciuta più rapidamente?"

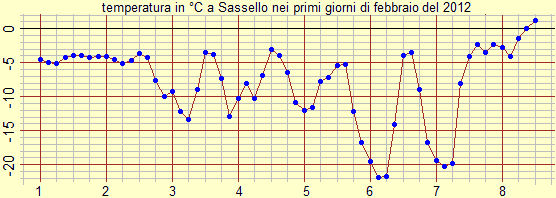
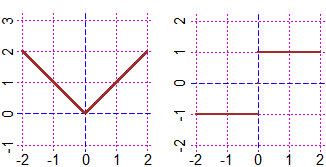
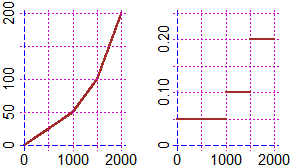
    Si può poi passare dalla quantificazione della pendenza alla sua rappresentazione grafica facendo riferimento a grafici più semplici, come i seguenti.
    Il primo  (che potrebbe rappresentare ad esempio coma varia il livello del liquido immesso nella cisterna raffigurata a lato al crescere del volume di esso)  è una sequenza di tratti rettilinei congiunti, affiancato dal grafico della sua pendenza, che è una sequenza di tratti orizzontali.
    Il secondo è il grafico di x → |x|; il grafico della sua pendenza è costituito da due semirette orizzontali, quella che parte dall'asse y alla quota 1 e prosegue a destra e quella che parte dall'asse y alla quota −1 e prosegue a sinistra.
    Poi si potranno considerare curve non costituite da tratti rettilinei.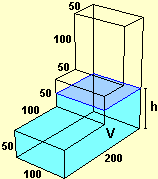 		  

   

    È facile mettere a fuoco come calcolare la derivata di una funzione in x0 (ossia come definire la pendenza della retta tangente in x0 al grafico della funzione) utilizzando il concetto di limite.

   

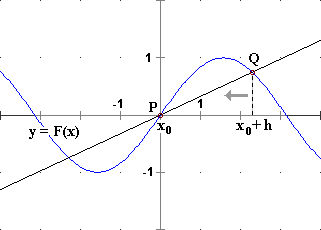
    Ed è facilissimo ottenere le derivate delle funzioni x → xn: ci si riconduce ad un banale calcolo in cui basta porre h=0 per avere il risultato.

lim h→0 (x+h)3 – x3
————
h
 = 
lim h→0 x3+3x2h+3xh2+h3 – x3
—————————
h
 = 
lim h→0 3x2h+3xh2+h3
——————
h
 = 
lim h→0 (3x2+3xh+h2)
 = 
3x2

    È opportuno, subito (e ritornandovi successivamente), metterne a fuoco una caratterizzazione geometrica:

    Sempre con considerazioni grafiche è facile mettere a punto che  D(k f) = k D(f)  (se moltiplico tutte le "y" per k la pendenza si moltiplica per k)  e che  D(f+g) = D(f)+D(g)  (se sommo, in corrispondenza delle stesse "x", le "y" dei grafici di f e di g, ottengo un grafico che man mano ha come pendenza la somma delle pendenze dei due grafici).
    In questo modo, in classe terza, siamo in grado di affrontare la derivazione delle funzioni polinomiali, essenziale per affrontare le prime formalizzazioni delle leggi della fisica.  Vedi qui per qualche riflessione a questo proposito.
    Alla fine della terza o in quarta, a seconda del tipo di scuole, si potranno poi introdurre le derivate di altre funzioni, privilegiando la messa in luce del significato geometrico alla giustificazione formale.

    Comunque, prima di questi sviluppi, dopo aver visto in casi semplici come si possono calcolare direttamente gli integrali definiti di alcune funzioni, occorre mettere a fuoco come l'integrazione può essere ricondotta ad una operazione di antiderivazione grazie alla formula fondamentale del calcolo integrale:

sia f continua in [a,b];  se G' = f  allora  ∫[a,b] f  =  G(b) − G(a)

    Non è il caso di dimostrare questo "teorema" (che potrà poi essere affrontato da chi proseguirà gli studi in ambito scientifico), ma va giustificato su alcuni semplici esempi, come il seguente, relativo a f: x → m·x.


∫ [x1, x2] m·x dx = 1/2·m·x2² − 1/2·m·x1²

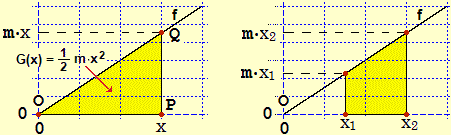
    Quest'esempio, per altro, assumendo il tempo come x, la velocità come f, corrisponde al calcolo dello spazio percorso fra il tempo x1 e il tempo x2 da un oggetto che si muove con velocità che cresce con accelerazione costante.

    Il calcolo degli integrali definiti utlizzando l'antiderivazione è l'aspetto più importante, che deve essere avviato in tutte le scuole,  così come possono essere introdotti il termine primitiva  (una primitiva di F è una funzione che viene "prima" dell'applicazione ad F della derivazione) come sinonimo di antiderivata  e, eventualmente, quello di integrale indefinito di F per indicare la funzione  x → ∫ [a,x] F  (che esprime l'area orientata tra grafico di F ed asse orizzontale compresa tra le rette verticali di ascissa a e di ascissa x).

    Nei successivi sviluppi relativi alle funzioni di una variabile (la concavità, le tecniche di integrazione, …) occorre distinguere i diversi livelli a cui giungere nei vari tipi di scuole.  In ogni caso, occorre privilegiare la comprensione delle idee rispetto all'addestramento alle tecniche (fine a sé stesso, e temporaneo) che non ha alcun senso nella formazione preuniversitaria.  Occorre piuttosto educare all'uso ragionato delle risorse (affidabili) disponibili in rete.  E occorre far superare gli steccati fra le diverse aree disciplinari  (ad esempio risoluzioni di equazioni, disequazioni e sistemi si avvalgono di concetti e strumenti presentati in questa voce, e concetti e strumenti relativi a tali temi servono per studiare aspetti qui discussi).   Per qualche idea in proposito vedi questa scheda di lavoro.

    Ci limitiamo a ricordare lo strano impiego di  ∫ f(x) dx  per indicare un generico termine g(x) tale che g'(x) = f(x).  È un uso che sopravvive per motivi storici, ma che è abbastanza ambiguo. È bene, dunque, fare (agli alunni) alcune osservazioni:
•  nel caso dell'integrale definito la variabile "integrata" è muta : si potrebbe scrivere  ∫ [-1, 3] f(x) dx  o  ∫ [-1, 3] f(t) dt  o  ∫ [-1, 3] f,  o usare una variabile diversa da x e t  in modo del tutto equivalente;  invece  ∫ f(t) dt,  ∫ f(x) dx  e  ∫ f(u) du  indicano termini diversi;
•  qualcuno usa l'integrale indefinito per indicare un insieme di termini:  ∫ f(x) dx = {g(x) + c / c numero reale}:  ad es.  ∫ 6x dx  starebbe per l'insieme costituito dai termini  3x2,  3x2 + 1,  3x2 + 2/3,  3x2 − 5, …, ovvero dai termini del tipo  3x2 + c  al variare di c in R;  altri lo usano per indicare un termine particolare che abbia come derivata  f(x);

•  la prima convenzione è la più corretta ma è meno pratica; in genere si usa la seconda convenzione, ogni tanto esplicitando, e ogni tanto no, la possibilità di aggiungere una costante, ossia qualche volta si scrive  ∫ 6x dx = 3x2 e qualche altra volta  ∫ 6x dx = 3x2 + c  lasciando al lettore la comprensione. WolframAlpha, come "compromesso", aggiunge un "+constant" in colore chiaro:

integral 6*x dx   fornisce   3*x^2 + constant.

    Sempre nelle scuole ad indirizzo scientifico è opportuno mettere a fuoco, per prevenire misoncezioni, le differenze "calcolistiche" tra derivazione e antiderivazione:  mentre le derivate delle funzioni "elementari" sono ancora "elementari" lo stesso non accade per l'antiderivazione;  ad esempio l'antiderivata di x → √(x³+1) non è elementare.  Ma non è affatto vero che non si sappiano "calcolare" ed esprimere come funzioni le antiderivate delle funzioni elementari.  Rimandiamo per questo alla stessa scheda di lavoro citata sopra.

    In tutti i casi per l'integrazione definita si può ricorrere al software (WolframAlpha o R ad esempio), o a questo semplice script, scaricabile sul proprio computer e modificabile per calcolare qualunque integrale. Ad esempio posso trovare che l'integrale tra 1 e 7 di x → √(x³+1) è (arrotondato) 52.049971104.

Ma per questo integrale si poteva ricorrere anche allo script visto sopra:

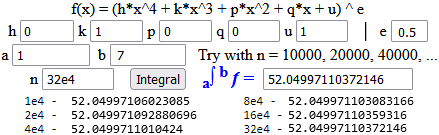
    Messa a fuoco l'idea che l'integrazione indefinita, in quanto antiderivazione, è un'equazione la cui soluzione è una funzione (con un parametro),  nelle scuole ad indirizzo scientifico si può accennare al fatto che, in quanto tale, essa viene chiamata anche equazione differenziale ed, eventualmente, accennare ad altri tipi di equazioni differenziali, appoggiandosi al software e alle diverse risorse informatiche gratuite, sempre nell'ottica di non soffermarsi su tecniche a questo livello non comprensibili e con l'obiettivo di dare l'idea di possibli sviluppi a chi eventualmente voglia proseguire gli studi in ambito scientifico.  Per qualche idea anche a questo proposito vedi questa scheda di lavoro.
    Ripetiamo, non è che certi argomenti non vadano affrontati perché solo dopo si potranno studiare in modo più generale e più approfondito anche dal punto di vista tecnico:  occorre, nei casi significativi, introdurli ad un primo livello, poi riprenderli ad un secondo, e così via.  Anche nella formazione universitaria di chi proseguirà gli studi in ambito scientifico si arriverà solo ad un livello intermedio di formalizzazione e di applicazione di essi.
 

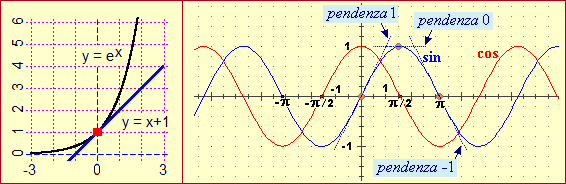
Funzioni esponenziale e logaritmo

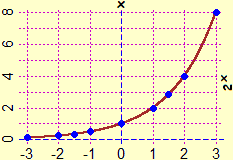        A lato è tracciato il grafico della funzione x → 2x e sono evidenziati i punti che rappresentano i valori che essa associa a  0  (1),  a 1  (2),  a 2  (4),  a 3  (8),  a −1  (1/2),  a −2  (1/2),  a −3  (1/8)  e a  −2  (1/4).  Sono evidenziati anche i valori associati a 1.5 e a −1.5; ricordiamo come sono calcolati:
21.5 = 215/10 = 23/2 = (23)1/2 = √8 = 2.82842…
2−1.5 = 2−3/2 = 1/23/2 = 1/√8 = 0.353553…
    Con un mezzo di calcolo ottengo valori anche per altri esponenti; per 2π con WolframAlpha ho ad esempio:
8.82497782707628762385642960420800158170441081527148…
    Ricordiamo come potrebbe essere svolto il calcolo in questi casi:

π = 3.1415926535897932384626433832795028841971693993751…
23 = 8≤ 2π ≤ 24 = 16
23.1 = 10√(231) = 8.5741877002… ≤ 2π ≤  23.2 = 10√(232) = 9.1895868399…
23.14 = 50√(2157) = 8.8152409270… ≤ 2π ≤  23.15 = 20√(263) = 8.8765557765…
.........
23.141592 = 8.8249738290… ≤ 2π ≤  23.141593 = 8.8249799460…
.........

    Quello che abbiamo visto ora è il modo in cui è definita la funzione x → 2x:  per x razionale è definita nel modo illustrato all'inizio di questa voce, negli altri casi è definita come abbiamo ora visto, in modo da essere continua, ossia in modo che all'infittire degli input infittiscano gli output.
    La funzione esponenziale può essere introdotta nel primo biennio (come si è visto nel documento relativo ai primi anni delle superiori), ma il suo significato deve essere ripreso al terzo anno, approfondendolo con i nuovi concetti di analisi matematica e intrecciandolo allo studio della sua funzione inversa, la funzione logaritmo.


 

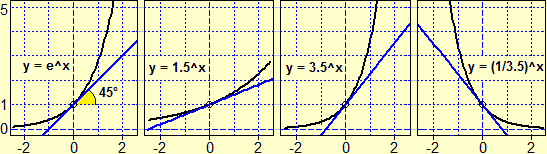
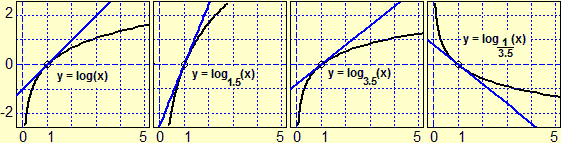
    Tra le applicazioni pratiche del concetto di logaritmo decimale, che gli studenti potrebbero ritrovare in altre discipline scientifiche e che si incontrano in vari contesti (anche medici), vi è il suo uso come estensione del concetto di ordine di grandezza,  che facilita la descrizione sia dei valori molto grandi (milioni, miliardi, …) che di quelli molto piccoli (milionesimi, miliardesimi) e la loro rappresentazione grafica.
    La figura a destra ne illustra l'uso per la rappresentazione degli audiogrammi.  Sotto viene rappresentato come le specie animali si distribuiscono per classi dimensionali (si vede, ad esempio, come vi siano poche specie di animali "grandi" e molte di animali "piccoli").		  

    Vedere esempi d'uso, come questi od altri, non è un "lusso", ma, piuttosto, è essenziale nell'insegnamento preuniversitario.  È del tutto senza senso, e dannoso per la comprensione degli alunni e per la costruzione di un'immagine attendibile della matematica, dare definizioni, fare esercizi ripetitivi, … senza vedere innanzi tutto esempi d'uso (e ruolo che hanno in questi) dei vari concetti e delle varie tecniche introdotte.  L'idea che la scuola preuniversitaria debba costruire gli "strumenti" lasciando all'università l'eventualità di mostrare come usarli per modellizzare e risolvere problemi è del tutto contraria, oltre che al buon senso, alla messa a fuoco della natura della scienza e della cultura e agli obiettivi della scuola di "tutti".
 

Lo spazio

    Riportiamo anche nelle riflessioni su questa fascia scolastica questa "digressione", fantastica ma molto concreta, sul concetto di angolo.  In essa sono contenute anche varie riflessioni sull'inopportunità di un approccio assiomatico all'insegnamento della geometria.  Questo è stato messo a fuoco solo alla fine del XIX secolo, soprattutto con la finalità di mettere a fuoco le diverse geometrie che si potevano definire cambiando alcuni assiomi.  I cosiddetti "Elementi di Euclide" (da non confondere con la "geometria euclidea"), significativi nella storia del pensiero, non hanno certo le caratteristiche di quella che, in matematica, è una presentazione assiomatica:  QUI è evidenziato come anche le dimostrazioni dei primi "teoremi" di Euclide non siano accettabili.

    Rinviamo al documento relativo ai primi anni delle scuole superiori la discussione e la esemplificazione di come introdurre e sviluppare (nell'ottica di una ripresa a "spirale") la matematizzazione dello spazio.  Ivi abbiamo anche esemplificato come possono essere introdotti elementi di geometria tridimensionale, elementi di geometria vettoriale e considerazioni sulle riproduzioni cartografiche, anche collegandosi con l'insegnamento di altre discipline.  Ivi abbiamo rinviato a questo documento per una discussione più approfondita dell'impostazione dell'insegnamento geometrico e per una rapida storia della geometria stessa (e per vari esercizi rivolti agli insegnanti).

    Richiamiamo ora, attraverso alcune immagini e qualche commento, alcuni degli altri temi affrontabili negli ultimi anni delle superiori.  L'obiettivo di buona parte dei contenuti nuovi da sviluppare in questa fascia scolastica non è tanto quello di far acquisire una buona padronanza tecnica di essi quanto quello di farne cogliere, anche operativamente, il ruolo nel contesto sociale e produttivo.  La principale finalità della scuola, soprattutto negli ultimi decenni, è di tipo culturale, non professionale.  Anche in relazione alle veloci trasformazioni che attraversano il mondo del lavoro e dell'economia, per un inserimento nel mondo del lavoro sono richieste più capacità di orientamento, comprensione dei processi, adeguamento ai cambiamenti tecnologici che informazioni iperspecializzate.  Occorre far cogliere i collegamenti tra i concetti generali e le tecniche, non insegnare conoscenze astratte e separatamente addestrare a pratiche ripetitive.  Questa è la sfida che la scuola deve affrontare, se non vuole continuare nel suo progressivo declino culturale e sociale.

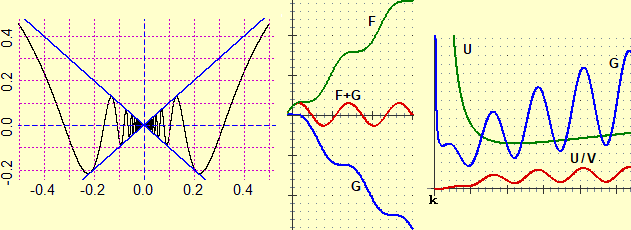
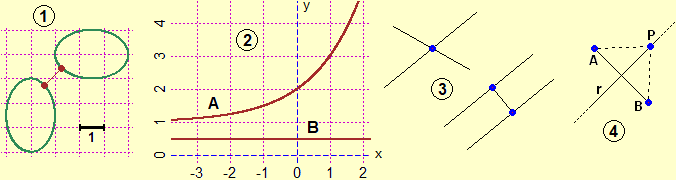
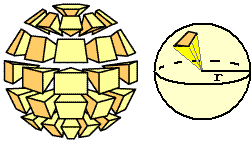
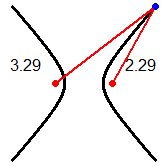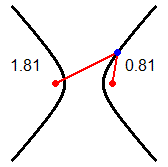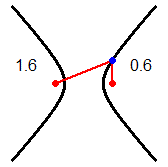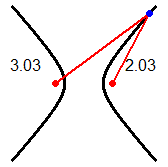
    Partiamo dal concetto di distanza.  Nel linguaggio comune la distanza è tra oggetti e figure, non tra punti.  Che senso ha, a scuola, fermarsi alla distanza tra punti?  L'immagine (1) illustra la distanza tra due curve (o tra due isole): è la minima tra le distanze di due generici punti che stanno su di esse.  Nell'immagine (2) la distanza tra le curve A (una curva avente y=1 come asintoto) e B (la retta y=1/2) è 1/2, ma non è la minima delle distanze tra due punti su A e su B:  esse formano un intervallo (1/2,∞);  la distanza è l'estremo inferiore di questo intervallo, cioè 1/2.  Occorre poi, correggere alcune misconcezioni spesso diffuse dalla scuola stessa, come quella secondo la quale due rette che mantengano la stessa distanza sono parallele, mettendo a fuoco che - vedi (3) - la distanza tra due rette è sempre costante, ed è nulla se sono incidenti.  Ed è utile mettere a fuoco come vari concetti possono essere definiti usando o no il concetto di distanza, come quello di asse di un segmento - vedi (4) - che può essere visto sia come costituito dai punti equidistanti dagli estremi che come la retta passante il punto medio del segmento e perpendicolare ad esso, come quello di bisettrice, che può essere definita sia come l'insieme dei punti equidistanti dai due lati dell'angolo che come la retta che lo divide in due angoli eguali.  Vedi qui per degli script che calcolino le distanze tra un punto e una curva e tra due curve.

    Occorre consolidare alcuni concetti di geometria tridimensionale, sia quelli richiamati nel documento relativo ai primi anni delle superiori, sia altri collegati al concetto di prospettiva (che dovrebbero essere già stati messi a fuoco nella scuola di base e sui quali si potrebbero realizzare sinergie con l'insegnamento di altre discipline: disegno, storia dell'arte, …); essi sono importantissimi sia nella storia della matematica che nelle sue applicazioni, sempre più presenti nella vita di tutti i giorni.  Non si tratta, anche in questo caso, di fare delle trattazioni approfondite, e interne alla matematica, ma di mettere in luce (ricorrendo all'uso, indispensabile del computer) idee e concetti, come messo in evidenza dalle figure seguenti.  I livelli di approfondimento si possono poi diversificare moltissimo in relazione al tipo di scuola e alla disponibilità a collaborare dei colleghi di altre materie.



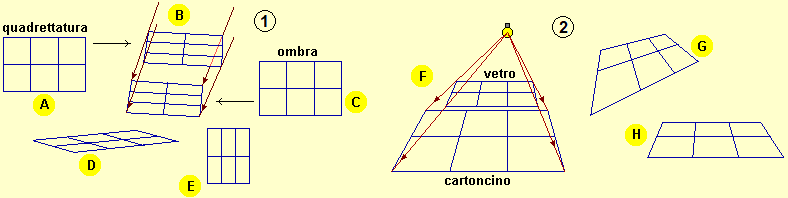
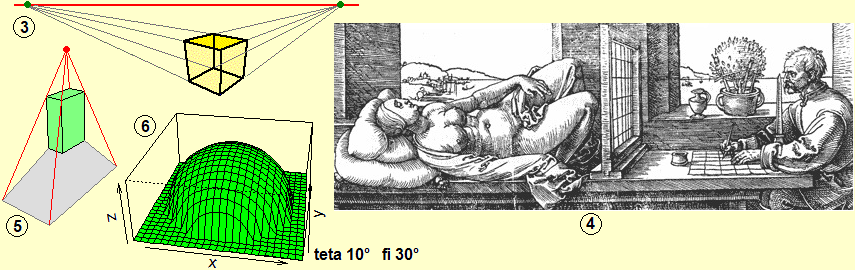
    Le coniche non costituiscono un tema matematico "fondamentale" da un punto di vista "tecnico" rispetto alla conoscenze di base da sviluppare. È tuttavia importante, culturalmente, avere un'idea dei collegamenti tra varie aree della matematica che le coniche mettono in luce. Alcune delle immagini presenti qui richiamano i contesti in cui parabole, ellissi e iperboli, pensate come curve tra loro indipendenti (non come "coniche"), hanno trovato molte applicazioni sin dalla antichità; sono argomenti facilmente affrontabili studiando le curve in generale, collegandosi anche ad altre discipline, per alcuni aspetti sin dalla scuola secondaria di 1º grado.  La seconda, la terza e la quarta delle figure seguenti illustrano, invece, come il termine "coniche" possa essere introdotto, verso la fine delle scuole superiori, in tutte le scuole:  rappresentando le coniche come intersezione fra un cono e piani diversamente disposti,  mettendo in luce che se guardo una conica dal vertice del cono mi appare comunque circolare,  evidenziando che col solo sguardo non posso distinguere quale tipo di conica sto osservando.





vedi qui 


    Nelle scuole ad indirizzo scientifico si può studiare come rappresentare analiticamente tutte le coniche e, eventualmente, come rappresentarle anche in forma polare (vedi la parte finale del documento a cui si è stati indirizzati poco sopra; per ulteriori approfondimenti vedi qui).

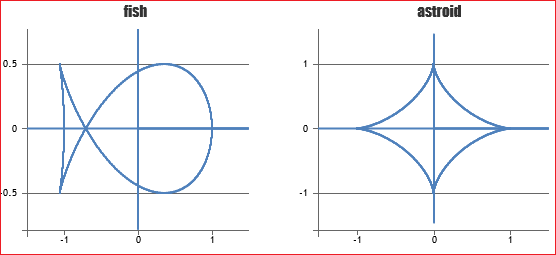
    Ma è forse più importante dare un'idea delle molte altre curve che possono essere descritte con delle semplici formule matematiche (vedi).

    Sui temi di geometria tridimensionale affrontabili nella parte finale delle scuole superiori ci siamo già soffermati poco sopra (discutendo della prospettiva e delle coniche) e nel documento relativo all'inizio delle superiori (vedi).  Ulteriori sviluppi da affrontare in tutte le scuole, con motivazioni elementari, sono i volumi di alcune semplici figure (parallelepipedi, cilindri, piramidi, coni, sfere) e, in particolare in quelle ad indirizzo scientifico, i vettori tridimensionali.  Per avere un'idea degli approfondimenti trattabili nelle scuole ad indirizzo scientifico vedi ad esempio qui.  Un'animazione che esemplifica concretamente come potrebbe essere affrontato il tema delle geometrie non euclidee, e dà alcune indicazioni bibliografiche:  Passeggiando sulle sfere.


 

La statistica e il calcolo delle probabilità

    Come è stato ricordato nelle sezioni precedenti, il fatto che gli strumenti statistici e probabilistici siano da utilizzare (e i cui esiti siano da interpretare) in contesti non puramente matematici è forse il motivo per cui essi sono spesso trascurati dai docenti (o sviluppati in modi episodici e per nulla corretti);  tutto ciò nonostante che, nei primi livelli scolastici, quest'area della matematica coinvolga solo strumenti comuni ad altri settori della disciplina.  Fino alla sezione precedente (vedi) abbiamo discusso della statistica e della probabilità in paragrafi distinti, mentre in questa, riferita agli anni finali della scuola superiore, le affrontiamo in modo più intrecciato ed esplicitiamo il legame tra esse mediante il teorema limite centrale, di cui gli alunni, negli anni precedenti, hanno implicitamente percepito l'esistenza  (hanno capito che in un esperimento statistico all'aumentare delle prove il rapporto tra numero delle uscite favorevoli e totale delle uscite tende a stabilizzarsi sulla probabilità).
    Ricordiamo che  qui  sono presenti link a programmi impiegabili per elaborazioni statistiche, e che  qui  si può trovare una breve storia del calcolo delle probabilità.

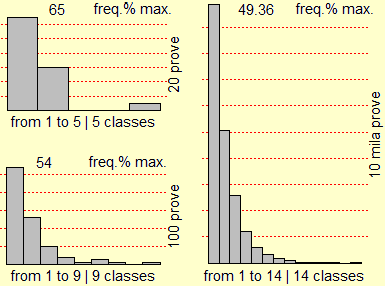
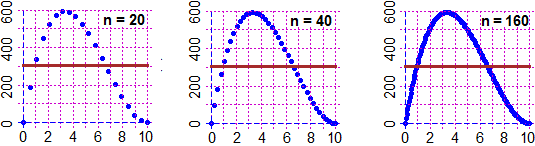
    Se non lo si è già fatto nel biennio, occorre mettere a fuoco che una variabile casuale discreta può essere non finita.  La figura seguente riporta gli istogrammi relativi a più esiti dell'esperimento (fatto a mano e simulato col computer) di contare quante volte occorre lanciare una moneta equa per ottenere l'uscita di "testa".  All'aumentare delle prove l'istogramma di distribuzione tende a diventare una figura illimitata, ma comunque con area finita, uguale a 1  (occorre far osservare agli alunni che questo non è una cosa strana:  sin dalla scuola di base sanno che 1/9 = 0.111… = 1/10 + 1/100 + 1/1000 + …).

 
1/2 + 1/2² + 1/2³ + … = 1
 
 
 

  

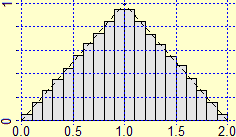    Dal lancio di due dadi si può passare allo studio della somma di due numeri tra 0 ed 1 ottenuti col "generatore di numeri casuali".  Si passa, in modo naturale, da un istogramma ad un triangolo, da una somma ad un integrale (vedi la figura a sinistra).  Questo (il passaggio dagli istogrammi alle funzioni di densità continue) per altro può essere un contesto per l'introduzione dell'integrazione che può precedere quello discusso poco sopra.

    Un altro esempio:  l'istogramma di distribuzione dei tempi di arrivo in una vendita televisiva tra una telefonata e l'altra e, sovrapposto, il grafico di una funzione che sembra approssimarlo.  Fenomeni di questo tipo (come la distanza temporale tra la venuta al semaforo di un'auto e quella della successiva, nel caso di un semaforo preceduto da un lungo tratto di strada senza impedimenti) hanno una distribuzione esponenziale.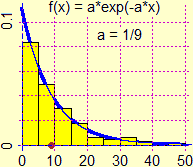

  

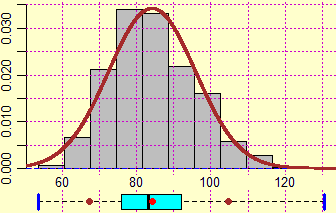
    Sopra alcuni esempi di leggi di distribuzione.  L'ultimo istogramma rappresenta una legge di distribuzione gaussiana che, al di là di quello che viene fatto credere spesso agli alunni, non si presenta molto spesso in natura  (si distribuiscono grosso modo in tale maniera le altezze delle persone adulte di un dato sesso appartenenti ad un certo gruppo razziale, le lunghezze dei pesci di una certa specie, …, le registrazioni con un cronometro manuale di una medesima durata temporale da parte di diverse persone, …).  A destra per esempio è riprodotto l'istogramma di distribuzione dei pesi registrati in Italia al primo contingente delle visite di leva (di maschi più o meno ventenni) nel 1987, che, come è evidente, non ha andamento gaussiano.
    Perché è importante la distribuzione gaussiana?  Perché è la media di pressoché tutti i fenomeni casuali, comunque siano distribuiti, ad avere andamento gaussiano, e questo ci consente di stimare la precisone del valor medio ottenuto o, nel caso si stia simulando un fenomeno, la precisone della stima ottenuta della probabilità che esso accada.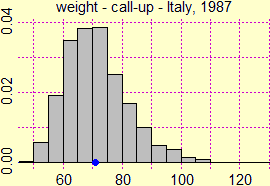 		  

       Più precisamente, sapendo che i pesi rilevati sono  N = 4170 e che la loro media è  m = 70.977, si ha che se ripetessi molte volte la prova con N altri individui della stessa categoria presi a caso otterrei altri valori della media, valori che comunque si distribuirebbero secondo una gaussiana, come quella raffigurata a fianco, con σ = sd/√N, dove sd è la cosiddetta "deviazione standard sperimentale" (radice quadrata della divisione per N-1 della somma dei quadrati degli scarti dal valor medio), 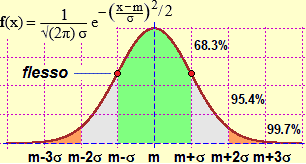ossia σ = 0.163 (vedi qui per i dettagli, di cui almeno l'insegnante deve esse consapevole).  Posso concludere che al 68.3%, nel 1987, il peso medio (in kg) di un italiano maschio ventenne è  70.977±0.163,  al 99.7% (ossia con pratica certezza) è  70.977±0.163·3 = 70.977±0.489, ovvero 71±0.5 kg.
    Altro esempio:  se con un apparato misuratore ad alta sensibilità ottengo le 7 misure (in una data unità di misura) 7.3, 7.1, 7.2, 6.9, 7.2, 7.3, 7.4, posso calcolarne la media (7.2000…), la deviazione standard (0.061721) e il suo triplo (0.185), e concludere che il "valore vero" della misura al 99.7% è 7.200±0.185.

    La proprietà ora richiamata costituisce il teorema limite centrale, che intreccia la probabilità e la statistica ed è alla base di tutte le applicazioni di quest'area della matematica (anche della realizzazione dei sondaggi che ci propinano, spesso malamente, i media televisivi).  Per inciso osserviamo che il fatto che la media di N variabili casuali con la stessa legge di distribuzione di media m al crescere di N tenda (probabilisticamente, nel modo sopra descritto) a m si chiama legge dei grandi numeri.
    Anche per valutare gli esiti di una simulazione si usa questa proprietà  (qui trovi qualche esempio).

    Non è importante che gli alunni, specie delle scuole non a indirizzo scientifico o tecnologico, memorizzino procedimenti e tecniche.  È importante che comprendano le idee principali, che mettano a fuoco che non tutto è gaussiano,  e che si affidino al software  (R - vedi qui - o, per cose semplici, WolframAlpha)  per affrontare qualche situazione significativa.  È bene, piuttosto, fare dei semplici esempi che costituiscano dei "vaccini" rispetto alle misconcezioni diffuse dai massmedia (ed a volte anche dal mondo dell'istruzione).  Ad esempio prendere dei dati distribuiti in modo gaussiano e considerare i cubi degli stessi dati, osservare come cambia la forma dell'istogramma di distribuzione, notare che, mentre la mediana dei nuovi dati è la mediana dei primi dati, ciò non accade per la media.  E, poi, fare dei tranfert ai contesti (se in una popolazione di pesci o in una collezione di fagioli le lunghezze sono distribuite in modo gaussiano, ciò non può accadere per i loro volumi e, quindi, neanche per le loro masse).

x1, x2, x3, …         x13, x23, x33, …
mediana = 5.005,  media = 5.002       mediana = 125.4,  media = 140.2

    Qui trovi un semplice script per integrare la distribuzione gaussiana:

    Approfondimenti affrontabili nelle scuole ad indirizzo scientifico o tecnologico sono discussi nella prossima voce.

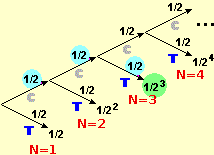
    Sia nel caso discreto che in quello continuo, per calcolare la probabilità di eventi si può ricorrere a questo semplice script, scaricabile sul proprio computer e modificabile. Ad esempio posso valutare la probabilità che lanciando tre dadi equi si ottengano almeno 2 uscite eguali (e congetturare che sia 4/9, per poi cercarne una dimostrazione):


 

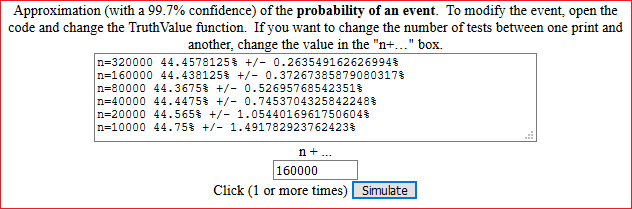
Relazioni tra due variabili casuali

    Le applicazioni principali della statistica, in ogni campo (medico, economico, biologico, fisico, …), sono rivolte allo studio dei legami tra diverse grandezze che variano casualmemte.  Anche in questo caso occorre dare a tutti gli alunni un'idea di questo ambito di impiego, non solo per dar loro strumenti per le eventuali scelte future nella prosecuzione degli studi, ma, soprattutto, per offrire loro elementi culturali per interpretare i fenomeni quotidiani, e valutare con criticità le informazioni e le interpretazioni fornite dai "media".
    Non servono conoscenze avanzate per acquisire questa consapevolezza.  Come abbiamo già detto più volte, non è importante memorizzare procedimenti e tecniche, a questo livello scolastico.
    In molti tipi di scuole ci si può fermare a due esempi di situazione, che non coinvolgono conoscenze avanzate (ma occorre mettere a fuoco che in altri casi è necessario ricorrere a strumenti più sofisticati).

    Primo esempio.  Discutendo del concetto di modello  (nel documento precedente)  abbiamo visto che il legame tra la distanza DS lungo la strada e quella DA in linea d'aria di Genova dalle altre località dell'Italia Settentrionale posso affrontarlo raccogliendo i dati relativi alle minime distanze stradali da Genova dagli altri capoluoghi di provincia (di Piemonte, Lombardia e Veneto) e quelli relativi alle distanze in linea d'aria, rappresentandoli graficamente e cercando di approssimare i punti con una retta.

    Questo approccio è illustrato a lato.  Ottengo una retta che passa circa per il punto 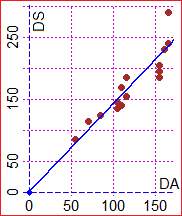(100, 150);  stabilisco che la relazione è circa DS = 1.5·DA.  Questo metodo "sperimentale" può essere sostituito con un metodo numerico, applicabile anche ad altre situazioni.  Basta considerare la somma dei quadrati delle distanze dei punti da una generica retta  y = M·x  e trovare per quale valore di M questa è minima.  Gli alunni sanno che basta calcolare la derivata di una funzione polinomiale di 2º grado e, poi, risolvere una equazione di polinomiale di 1º grado.  A questo punto si può usare anche un algoritmo che svolga questi calcoli automaticamente:: vedi questo script, o:

   

# Ad es., usando R (vedi qui):
da = c(55, 70,155,160,155,115,105,165,110,115, 85,165,110,155,105)
ds = c(85,115,205,230,185,185,145,240,140,155,125,290,170,195,135)
Plane(0,170, 0,300); POINT(da,ds, "brown")
regression(da,ds,0,0)
# 1.42 * x 
f = function(x) 1.42*x; graph1(f, 0,200, "blue")

    Secondo esempio.  Appendo differenti oggetti ad un elastico. Siano F il loro peso (in g) ed H (in mm) l'allungamento dell'elastico.  Riesco a determinare i valori di H con la precisione di 2 (mm) e quelli di F con la precisione di 5 (g).  Posso rappresentare i punti sperimentali con dei rettangolini.  So che (nell'intervallo di pesi considerato) tra H ed F c'è una relazione lineare H = k·F.  Prendo come approssimazioni per difetto ed eccesso di k i valori corrispondenti alle pendenze delle rette di minima e massima inclinazione passanti per (0,0) e per tutti i rettangolini. 

 H |  F
15 | 260
20 | 380
39 | 710
52 | 990
   
(990-5)/(52+2) = 18.24074         (710+5)/(39-2) = 19.32432       F = k·H,  k = 18.8±0.6

    Le immagini seguenti ricordano altri temi affrontabili (utilizzando software standard gratuito, come ad esempio R) nelle scuole ad indirizzo scientifico, privilegiando la comprensione degli aspetti concettuali rispetto alla tecnica.

    In un caso come il precedente, ma in cui non conoscessi la precisione delle varie misure, posso determinare l'intervallo in cui al 90% (o con un'altra probabilità) cade la pendenza della retta.  In questo caso ottengo  che sta tra 18.03658 e 19.35311.   



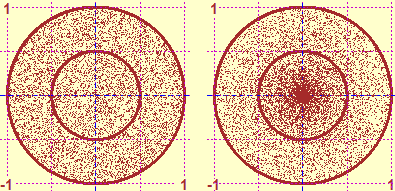          Che cosa significa "prendere a caso"?
    Anche nel caso bidimensionale dipende dalla legge di distribuzione secondo la quale lo si fa.

    A fianco la rappresentazione di due differenti modi per generare la caduta di un punto in un cerchio di centro (0,0) e raggio 1.

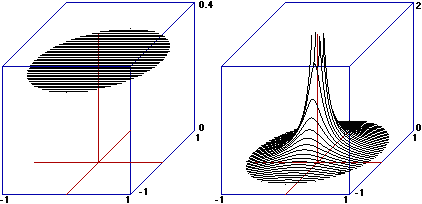
    A fianco, sulla sinistra, la rappresentazione grafica delle distribuzione di (X,Y) con X e Y altezze di un uomo e una donna sorteggiati a caso.
    Al centro, quella con X e Y altezze di marito e moglie di una coppia sorteggiata a caso, e, a destra, un possibile grafico di dispersione sperimentale della stessa distribuzione (uomini più alti tendenzialmente sposano donne più alte: non è affatto vero che l'amore è cieco!).
    In entrambi i casi X ed Y sono dipendenti l'una dall'altra,  nel secondo caso sono anche correlate tra loro.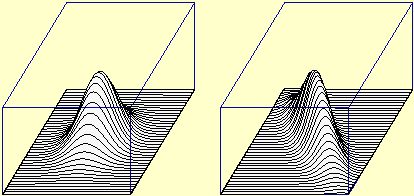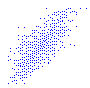 		       

    Il coefficiente di correlazione tra due insiemi di valori accoppiati esprime un valore tanto più vicino ad 1 o a −1 quanto più i due insiemi di valori sono approssimabili con una relazione lineare del tipo y = a·x+b:

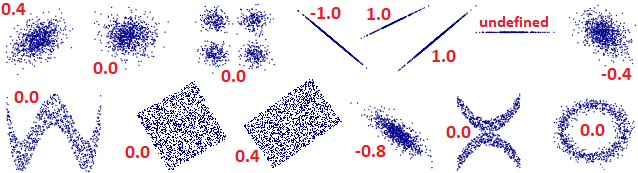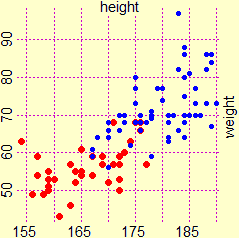           I punti nel diagramma a fianco rappresentano altezze e pesi degli alunni di un corso universitario; essi sono molto allineati (vi è un alto coefficiente di correlazione, 0.78).  Ma se osserviamo solo i punti (rossi) corrispondenti alla popolazione femminile abbiamo un'impressione diversa (il coefficiente di correlazione è 0.52).
    La statistica evidenzia solo delle relazioni numeriche tra i dati, non delle relazioni di causa-effetto, per studiare le quali sono necessarie conoscenze e studi specifici dell'area coinvolta!

    Un'indagine sul peso dei maschi tra i 45 e i 55 anni di un certo stato dà gli esiti grafici rappresentati graficamente sotto a sinistra.  I rilevamenti sono 825.  Si è provato a sovrapporre all'istogramma una gaussiana con la stessa media e la stessa deviazione standard.  Sembra che ci sia una discreta corrispondenza.  Posso assumere che l'andamento sia gaussiano?
     Assolutamente no!
    Infatti per valutare questa corrispondenza si calcola un certo valore, chiamato χ2, che dipende dai dati e dalla loro numerosità (si ottiene 27.07).  Poi lo si confronta con il grafico (tracciabile facilmente col computer) che rappresenta come si distribuirebbe χ2 se l'andamento fosse effettivamente di tal tipo (ossia gaussiano).  Si vede che il suo valore mediano è 7.34, molto minore di 27.07, così come lo è il 95º percentile (15.51).  È sicuramente da scartare l'ipotesi che l'andamento sia gaussiano: 27.07 è un valore altamente improbabile.

       
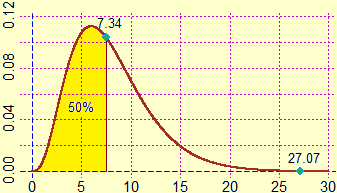2.73−5%   5.07−25%   7.34−50%   10.22−75%   15.51−95%

    Approfondimenti di tutti questi aspetti sono reperibili qui.
 

Approfondimenti di analisi matematica

    Vi sono altri aspetti dell'analisi matematica che possono essere presentati in tutti i tipi di scuola e che possono essere approfonditi in quelli ad indirizzo scientifico e tecnologico.  Il primo è la possibilità di approssimare intorno ad un punto tutte le funzioni più volte derivabili con funzioni polinomiali.  A fianco sono illustrati i casi più utili  (per 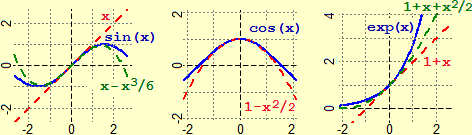x → 0, sin(x) ≈ x e sin(x) ≈ x−x³; cos(x) ≈ 1−x², exp(x) ≈ 1+x e exp(x) ≈ 1+x+x²), che, al di là della loro memorizzazione, possono essere messi a fuoco in tutte le scuole  (lasciando a quelle ad indirizzo scientifico e tecnologico la loro generalizzazione affrontando il tema dei polinomi, e delle serie, di Taylor).   

    Nei primi anni di scuola gli alunni hanno preso confidenza con molte funzioni a più input (somma, prodotto, media, …), e molte altre ne hanno studiato negli anni successivi.  Alla fine delle superiori è bene che tutti vedano, con semplici esempi, come siano rappresentabili graficamente le funzioni a 2 input e 1 output reali (generalizzando casi di analoghe funzioni ad 1 input):

   

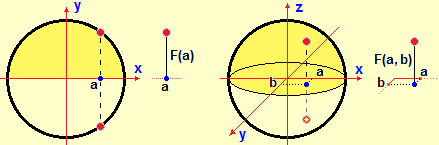
    Si possono mettere a fuoco i collegamenti con la lettura delle curve di livello delle carte geografiche e, volendo, utilizzando il computer, visualizzare i grafici di alcune funzioni e le relative curve di livello.  In scuole ad indirizzo scientifico o tecnologico si possono esplorare i collegamenti con i temi dello spazio e delle relazioni tra variabili casuali discussi in punti precedenti.  Per qualche idea sugli sviluppi affrontabili in queste scuole  (hessiano, gradiente, serie di Fourier, …)  si veda ad esempio qui e qui.


 

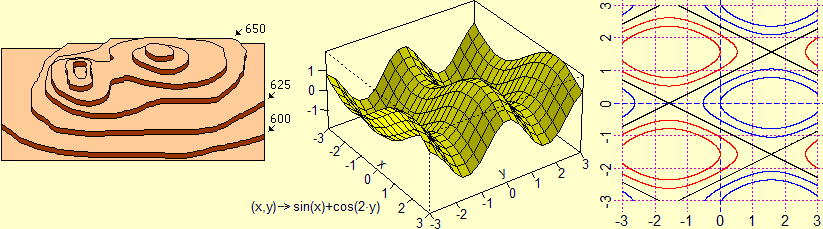
         Vi sono anche applicazioni significative che possono essere accennate e di cui si può comprendere facilmente la "matematica" retrostante, come le spline cubiche: curve costituite da tratti di curve polinomiali di terzo grado che si raccordano in modo che le derivate prima e seconda da destra e da sinistra siano eguali (vedi).
    A sinistra, una figura (vedi qui).
    Un altro esempio: la sezione di un bacino a partire dai rilevamenti di alcuni livelli di profondità:
 


 

Altro

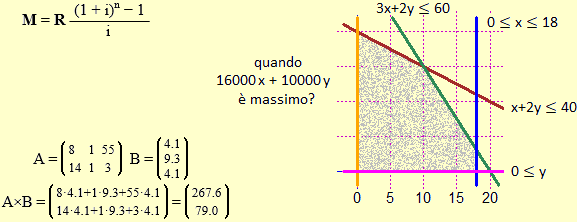
    Accenniamo ad altri temi che possono essere affrontati negli ultimi anni di alcune scuole ad indirizzo economico o tecnico, in cui è decisivo l'utilizzo del software:  la matematica finanziaria e la programmazione lineare (vedi qui e qui), e il calcolo matriciale, con i suoi variegati impieghi in molte aree della matematica (vedi qui e qui).
 


 

Diversificazioni didattiche, e considerazioni conclusive

    Discutendo del primo biennio abbiamo osservato come il livello di approfondimento possa essere diverso al variare del tipo di scuola, e come possano differenziarsi anche gli intrecci con le altre discipline.  Negli anni finali, come abbiamo visto, sono diversi i livelli di approfondimento a cui si può arrivare e i temi stessi che si possono affrontare differiscono a seconda dell'indirizzo scolastico.  In tutti i tipi di scuole occorre, comunque, dare un'idea dei vari impieghi della matematica, in modo che le eventuali scelte di prosecuzione degli studi non siano orientate da una visione piccola e distorta della disciplina, che spinga  o  alla scelta di studi universitari di area matematica da parte di persone che pensino ad essa come qualcosa di staccato dalle altre forme di sapere, basato su attività meccaniche o sulla ripetizione di forme di ragionamento stereotipate,  o  alla scelta di altri studi da parte di persone, invece, curiose, interessate agli intrecci fra ambiti diversi, alla ricerca di strategie risolutive di problemi e alla comunicazione comprensibile dei procedimenti messi a punto.

    Abbiamo più volte osservato come il software, scelto in modo opportuno, possa facilitare la gestione didattica di molti contenuti, consentendo di affrontare, specie negli ultimi anni delle superiori, temi concettualmente, ma non tecnicamente, alla portata degli alunni, e con diversi livelli di approfondimento in situazioni scolastiche diverse.  È importante mettere a fuoco come la diffusione dei sussidi multimediali sia uno degli aspetti che più mettono in discussione l'attuale ruolo dell'insegnante:  è inevitabile che il docente sia tecnologicamente "meno avanzato" degli alunni, ma ciò non deve risolversi da parte sua (come spesso accade) nell'evitare le nuove tecnologie o nell'appoggiarsi a desueti sussidi di cui si è appreso l'uso parecchi anni prima.  Occorre rapportarsi in modo diverso con gli alunni, occorre farsi "spiegare" da essi quali sono le nuove tecnologie che loro usano e, in cambio, dare a loro le conoscenze e gli strumenti per padroneggiarle culturalmente.  In particolare il docente deve "insegnare" cosa, come, dove, … cercare in rete e in quale modo valutare le cose che vi si trovano.

    La matematica ha la specificità di non essere caratterizzata da una particolare area di problemi o di fenomeni che cerca di modellizzare (come la fisica, la storia, la linguistica, …), bensì dalla tipologia degli artefatti che impiega per la costruzione dei modelli, e che vengono utilizzati in tutte le altre discipline.  Abbiamo visto che i concetti nati come "astrazioni" a partire da situazioni concrete diventano man mano degli oggetti "concreti" dai quali partire per mettere a punto nuove astrazioni, in una spirale senza fine.  Il sapere matematico, che nasce dai contesti modellizzati, si organizza, diversamente dalle altre discipline, non sulla base dei contesti, ma dei rapporti e delle analogie strutturali tra i suoi artefatti.  L'acquisizione, operativa, del ruolo e del significato di questa natura astratta deve essere graduale e, contestualmente, si deve, gradualmente, mettere a fuoco la funzione delle definizioni e delle dimostrazioni.  Sembra ovvio (ma non lo è per gli autori dei libri di testo più diffusi) che l'obiettivo della scuola debba essere la costruzione del significato di queste, non l'affastellamento, temporaneo e incompreso, di enunciati, formulazioni e ricette.

    Ovviamente, occorrerebbe che, poi, a livello universitario, non si procedesse, come purtroppo non di rado accade, con supponenza, senza alcuna riflessione sugli obiettivi dei livelli scolastici precedenti, senza riflettere sulla natura (tecnica e storica, in breve "culturale") delle definizioni, delle dimostrazioni, dei rapporti tra le varie aree disciplinari, con atteggiamenti nei confronti degli studenti che, forse un po' caricaturalmente, potremmo rappresentare con frasi del tipo "ripartiamo da zero, buttate a mare tutto quello che avete studiato, che ora vediamo che cos'è la matematica!".

    E questo, purtroppo, vale, non di rado, anche per i corsi orientati alla didattica della matematica, che spesso sono incentrati solo sulle conoscenze di base, non di rado presentate in modo separato le une dalle altre, e che quasi sempre trascurano le riflessioni sui concetti affrontati nelle scuole superiori, che invece potrebbero innescare delle considerazioni sui modi diversi in cui i concetti devono essere presentati nelle diverse fasce di istruzione, considerazioni che per altro si possono riferire ad esperienze didattiche ancora "calde" per gli studenti.

    Infine, come più volte osservato, occorre tener conto che il rinnovamento continuo della matematica, dei suoi usi, delle sue interazioni con le altre discipline, delle tecnologie disponibili, delle opportunità offerte dalla rete  richiedono che parte dei contenuti e delle tecniche, divenute obsolete, siano via via ridimensionate o buttate a mare per dare spazio a nuovi contenuti e nuove tecniche matematiche, e ad atteggiamenti che consentano di reperire, selezionare ed usare quanto i nuovi media propongono.  La matematica è viva.
 

online software