Continuity

    We have given the concept of continuity in this way:  let F be a function defined in an interval  [a, b]; if as the inputs are denser also the outputs are denser, then F is said to be continuous in [a, b].  Furthermore, if F is a function defined in any set I of real numbers, it will be said that F is continuous in I if it is such in every interval [a, b] contained in I (for example  x → 1/x  is continuous in R−{0}).

    In this way the continuity of the real functions of a real variable has been introduced only on intervals, not at points, through what is traditionally assumed as the definition of uniform continuity.  This choice is the standard one in the field of constructive mathematics and is made in various calculus manuals (for example: Lax-Bernstein-Lax, "Calculus with Applications and Computing").
    On the usual definition it will be possible to return to the following classes, focusing on the following theorem, known as the small-span theorem:

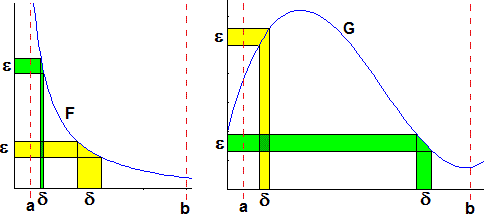
    The concept of "uniform continuity" (in an interval) differs from that of "continuity" (in all points of the interval) only, in particular cases, on non-closed intervals.  For example, in the drawing below, F and G are uniformly continuous in each closed interval contained in the interval (a,b);  instead if we were referring to the interval (a,b) we would have that F (assuming that F(x) → ∞ as x → a+) is not uniformly continuous in it, while it is continuous in every point of it.  This, however, does not create contradictions or doubts:  using the initial definition we had said that a function is continuous in a set of points (which can be an open interval or a union of intervals) if it is is continuous in every closed interval in it content.