Numeri, figure, formule, … per razionalizzare l'incerto
Carlo Dapueto - DiMa
25 novembre 2013 - ore 15:30-17:30
http://macosa.dima.unige.it/unite
Questa "conferenza" non cercherà di fare un bel discorso, ma tenterà di
dare (anche attraverso la presentazione di alcuni "esercizi") varie idee su cui le persone
possano pensare anche successivamente. Tutto quanto
verrà presentato e discusso è accessibile via rete, dall'indirizzo
soprastante.
Questo è un documento Html; sono presenti dei "link" attivabili
"cliccando" >>> (se il link non viene aperto in una nuova finestra ma sostituisce il precedente contenuto,
poi ritorna alla finestra precedente). Vedremo dopo il ruolo delle "finestre"
qui a sinistra.
Alcuni degli esempi fatti contengono anche delle parti calcolistiche;
saranno presenti collegamenti, per gli interessati, a come svolgere questi "calcoli",
che non saranno, comunque, necessari per seguire il discorso affrontato.
Tre o quattro esempi sono già stati illustrati in una precedente conferenza. Li ho
lasciati più meno intatti per facilitare l'individuazione di connessioni
tra le due presentazioni.
IL TITOLO ...
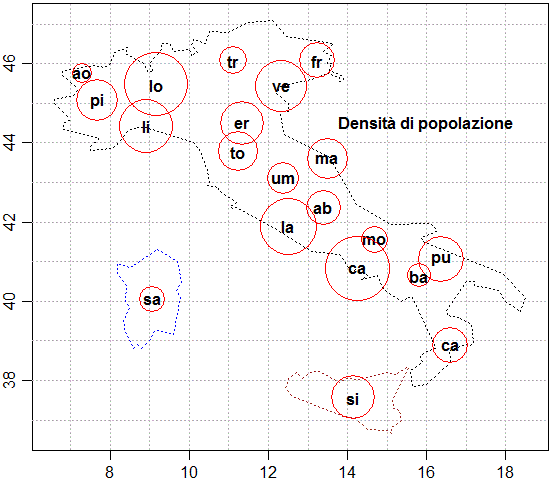
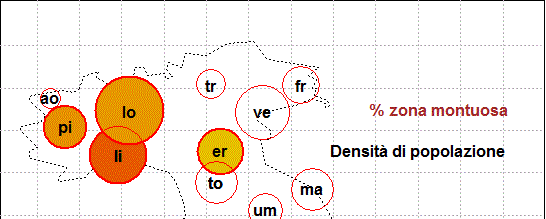
Queste figure danno idea del legame tra numeri (i dati), figure (le dimensioni dei cerchi, la loro
collocazione, i colori - vedi), formule (con cui
sono state costruite le figure a partire dai dati), …


Quali informazioni in più ho ottenuto/elaborato rispetto ai dati iniziali?
I PRIMI ESEMPI
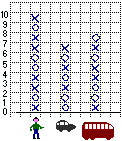
| Prima elementare, senza avere ancora padronanza dei numeri Nell'istogramma a quadretti a lato ogni alunno ha indicato il modo (a piedi, in automobile o coll'autobus) in cui di solito arriva a scuola. I maschi hanno usato una crocetta (x), le femmine un cerchietto (o). |
|
 | |
| Che cosa posso concludere, statisticamente, anche senza usare i numeri? | |
Scuola elementare
Due diverse rappresentazioni grafiche della temperatura in una particolare
città italiana alle dodici nei giorni di un dato mese (quale? ottobre): i grafici e gli
istogrammi di distribuzione.
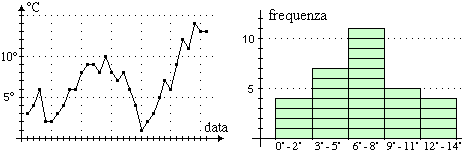
Quali diverse informazioni danno le due rappresentazioni?
|
Scuola media inferiore Da un'indagine svolta in un certo paese risulta che i giovani tra i 14 e i 19 anni spendono mensilmente 67.60 € così ripartiti: |
| |||||||||||||||||||
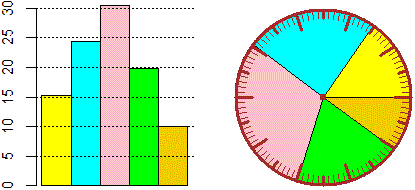 | ||||||||||||||||||||
| Diversi modi di rappresentare una "distribuzione" | ||||||||||||||||||||
|
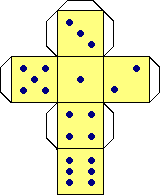
Ancora scuola media inferiore (1) Sta per disputarsi la partita Roma-Juventus. Gigi ritiene che la Roma 30 su 100 vincerà e 40 su 100 pareggerà. Qual è la probabilità per Gigi che vinca la Juventus? >>> (2) Qual è la probabilità che lanciando un dado esca un numero pari? >>> (3) Un dado da gioco viene costruito con del cartoncino secondo il modello raffigurato a lato. Quale, fra le seguenti, è la probabilità con cui esce uno? 16.7% 30.5% 9.3 % >>> (4) Lancio una moneta equa fino a che esce testa. Voglio studiare quanti lanci devo effettuare. Quanti sono i casi possibili? (ovvero, c'è un numero massimo di lanci che devo effettuare?) |
 |
Che cos'è la probabilità?
Perché non ha alcun senso definirla come
Discussione.
>>> (guarda solo due  )
)
IL GENERATORE DI NUMERI pseudoCASUALI
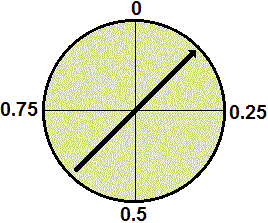 |
Se faccio ruotare la freccia in un dispositivo, ben oliato e simmetrico, come quello a lato (la freccia è imperniata nel suo baricentro), qual è la probabilità che esca un numero tra 0 e 0.5? e tra 0 e 0.25? e tra 0 e 0.05? e tra 0 e 0.005? e la probabilità che esca "esattamente" 0.25? |
|
Se U è una variabile casuale a cui si è associato, come
insieme di valori su cui può variare, un insieme di oggetti
matematici {a1,a2,a3,…}, dotare
U di una legge di distribuzione vuol dire descrivere
come calcolare i valori di una misura di probabilità Pr per
gli eventi |
Le uscite di una "freccia" come la precedente sono simulati in tutti i mezzi di calcolo da un oggetto chiamato generatore di numeri pseudocasuali. Perché c'è "pseudo"? ...
La statistica, oggi, si fa quasi solo impiegando il computer, in quanto i dati da analizzare sono molti, e la si fa usando software specifico. Le uscite di una "freccia" come la precedente sono simulati in tutti i mezzi di calcolo da un oggetto chiamato generatore di numeri pseudocasuali. (perché c'è "pseudo"? ...)
Noi faremo riferimento ad R, il programma standard a livello mondiale per le elaborazioni statistiche, che si può scaricare seguendo le indicazioni presenti qui
Vediamo un primo esempio di uso di R e, poi, l'esito del lancio di due dadi equi, con i comandi seguenti:
runif(1); runif(4)
n <- 1e5; U <- runif(n); mean(U)
hist(U, probability=TRUE, col="yellow")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
#
n <- 10000
U1 <- floor(runif(n)*6)+1; U2 <- floor(runif(n)*6)+1
dev.new(); hist(U1+U2, seq(1.5, 12.5, 1))
dev.new(); hist(U1+U2, seq(1.5, 12.5, 1),freq=FALSE)
summary(U1+U2)
Per commenti alle ultime uscite vedi qui
PROBABILITÀ E STATISTICA
Il Calcolo delle Probabilità e la Statistica sono evidentemente collegati, ma non
sono la stessa cosa e non si occupano esattamente delle stesse cose.
Ad esempio l'esempio (1) precedente affronta una questione
probabilistica che non ha alcun senso considerare dal punto di vista statistico.
Analogamente, alcune statistiche non danno luogo a successive valutazioni probabilistiche.
Noi qui ci preoccuperemo soprattutto di alcuni esempi in cui queste due aree della
matematica sono fortemente intrecciate, fino a confondersi.
Vedremo soprattutto esempi applicati, in quanto la statistica e il calcolo delle probabilità, più di altre aree della matematica, vivono degli intrecci con altre discipline. Un esempio di applicazione a questioni linguistiche.
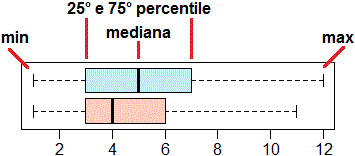
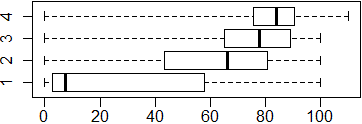
Questo collegamento permette di accedere a un brano che pubblicizza l'area del Porto Antico di Genova, sia in italiano che in inglese. Successivamente sono riprodotti gli istogrammi della distribuzione della lunghezza delle parole delle due versioni e i corrispondenti box-plot.
|
1 | 0 2 | 000000 3 | 000000000 4 | 00 5 | 0000000 6 | 00000000 7 | 0000 8 | 000 9 | 00 10 | 0 11 | 0 12 | 000 |
1 | 0 2 | 0000000 3 | 000000000000000 4 | 00000000000 5 | 00000 6 | 000000 7 | 00 8 | 000 9 | 00 10 | 11 | 0 |
 |
ATTENZIONE ...
| È frequente trovare (sui giornali, alla televisione, …) rappresentazioni scorrette: ad es. per il confronto del consumo di vino per abitante di 90 litri con quello di 60 litri si può trovare il disegno di una bottiglia alta 1.5 volte la bottiglia che rappresenta i 60 litri (90/60 = 1.5) invece del disegno di una bottiglia che abbia volume pari a 1.5 volte quello dell'altra bottiglia. | 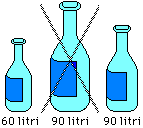 |
Altri errori sono più nascosti. Ad esempio in relazione alla quantità di cifre con cui vengono descritte le statistiche >>>
| La scelta di scale opportune è importante al fine di rendere più leggibile il grafico o più evidente il fenomeno rappresentato. Nei giornali sono usate per indurre a valutazioni particolari i lettori: i due grafici a fianco rappresentano la stessa tabella di dati ma suggeriscono valutazioni diverse sull'evoluzione del fenomeno. | 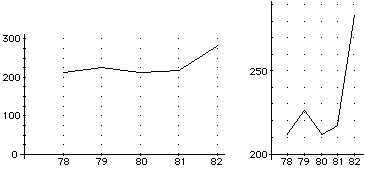 |
Un altro esempio in cui le rappresentazioni statistiche possono indurre a conclusioni fuorvianti. Ecco che cosa può accadere in relazione alla scelta di come realizzare un istogramma: >>>
Non è facile fare valutazioni probabilistiche. Un semplice esempio: >>>
Il calcolo della probabilità non basta: >>>
I vaccini. I test sanitari.
Un certo test sanitario per valutare la presenza (esito positivo) o
assenza (esito negativo) della malattia X ha attendibilità del
95% (in caso di presenza c'è il 95% di probabilità che
l'esito sia positivo , in caso di assenza il 95% di probabilità
che sia negativo). Si sa da statistiche serie che l'1% della
popolazione è affetta dalla malattia X. Se per una persona
il test dà esito positivo, qual è la probabilità
che essa sia realmente malata? È molto lontano dal 95% (è il 16%).

GLI OCCHIALI che la probabilità e la statistica mi offrono
L'ultimo esempio visto ha già messo in luce questo aspetto.
La probabilità per superare pregiudizi: >>>
... anche nel gioco d'azzardo: >>>
Cose che ad occhio non vedrei: morti per classi di eta` in Italia nel 1881-1890, nel 1951, nel 1988, nel 2006:
Altre applicazioni (per testare farmaci) in campo medico: >>>
APPROFONDIMENTI ...
Accenniamo ad alcuni esempi su questioni più approfondite.
Chi vuole può vedere più in dettaglio questi aspetti o
usando il menu qui a sinistra (provate ad esplorarlo) o andando
qui
(vedi anche "vol.1", "vol.2", …)
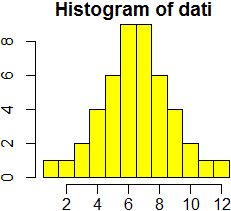
La strana idea che tutto sia GAUSSIANO |
 |
La correlazione: uno >>> due >>>
La regressione: una retta di regressione >>> e un polinomio di regressione >>>
|
Una correlazione statistica è indice di una relazione di causa-effetto? In un ospedale vengono rilevati i seguenti dati, relativi alla frequenza cardiaca a riposo di 10 individui e i loro anni complessivi di istruzione. |
|
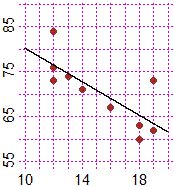 |
I dati, rappresentati graficamente, sono approssimati "al meglio" dalla retta:
battiti = -1.862·anni + 98.79 Risulta esserci una forte associazione tra una lunga scolarizzazione e una bassa frequenza cardiaca, ma questo non indica una relazione di causa-effetto! C'è solo un legame di entrambe le variabili con uno o più fattori impliciti (potrebbero essere l'informazione sui regimi alimentari che tendenzialmente cresce all'aumentare dell'istruzione, il tempo o la voglia di svolgere adeguata attività fisica che tendenzialmente cresce quando si svolge un lavoro che lascia più tempo ed energie per essa, il fatto che un miglior reddito consente di acquistare alimenti migliori, ...) |
• Con
WolframAlpha, a cui si può accedere online da
qui
(e per cui qui
puoi trovare molti esempi d'uso, relativi alla statistica, oltre che alla matematica, alle scienze, alla geografia, ...)
puoi mettere ad esempio la riga di
comandi
solve (x+7)/(x-1) = a*x for x
per ottenere:
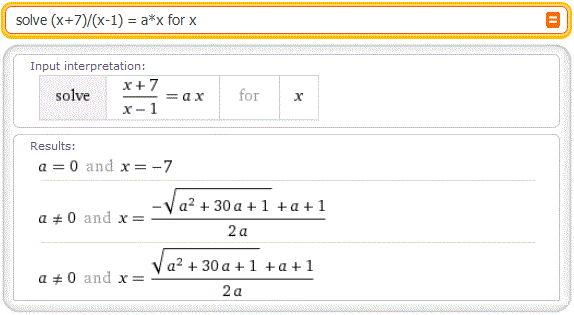 |
Per altri esempi vedi, ad esempio:
mathworld subject descriptive statistics
mathworld subject statistical plots
mathworld subject continuous distributions
gaussian distribution
discrete distributions