First example:

I enter the data by clicking on [Enter], then I click [Calculate].

HELP:
• You can resize. You can draw 1, 2 or 3 histograms to compare them.
• If you open the file by pressing the right mouse button you can select "open in a new window".
• Go back, or reload the file, for new data series, or CLICK to use a new window.
• With Alt_Print you can copy the page and paste it into Paint or other applications.
• Do not change the page size if you want to compare other histograms.
• To compare different histograms you can fix the ratio between percentages and column lengths by putting a number in the box to the right of the "help" button (with 100, columns of a standard length, with a larger number [200, 300, ...] columns of shorter length, with a smaller number [90, 80, ...] columns of greater length.'

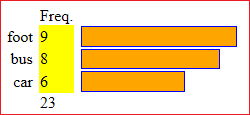
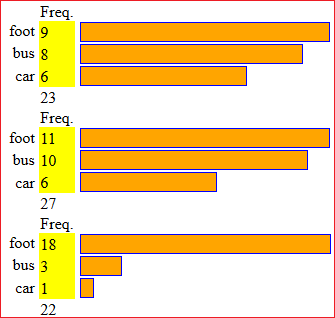
Second example.  How to compare different histograms: I can put up to 3 data sequences in name/frequency, name2/frequency2 and in name3/frequency3.  The histograms are plotted all occupying the same space.  But if in the box to the right of [HELP] I put a number (as explained in the Help) they are represented using the same percentage scale: in the example below (where I put 130, in order to make the histograms smaller) the column of maximum length is that of the third histogram which represents 18 out of 22 (81%); the second column, which represents 11 out of 27 (41%), is about half as high.  Even without explaining this aspect to the pupils in detail, they can be told that the representations take into account that (for example) 18 out of 22 is "greater" than 11 out of 27.
Alternatively you can use th sequence bar graphs script: see examples.

 

Third example:

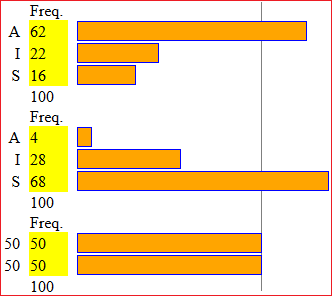If I want to introduce vertical lines I can proceed like this (and then use Paint or ...). If I introduce two equal frequencies (eg 50 and 50) I can find the line corresponding to 50. If I introduce 4 equal frequencies (eg 10, 10, 10 and 10) I can find the corresponding line at 25. Etc.

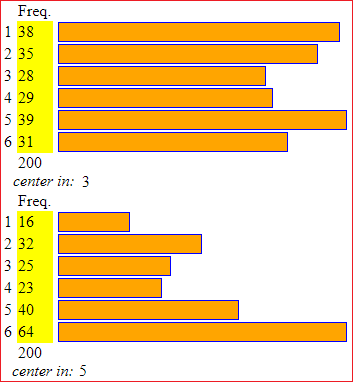
Fourth example: If I throw 200 times a "real" game die and a game die made of cardboard like the following, I get histograms like those shown on the side. "Center" represents the column in which the central value of the data falls. In the first case the die is balanced, ie the various faces are more or less equally probable; the center is 3; repeating the test I could get 4.  In the second case, face 6 (the one opposite the heavier face, with 3 glued tabs) tends to come out much more frequently; the center is 5, greater than 3 and 4.   In the case of the previous data I get:

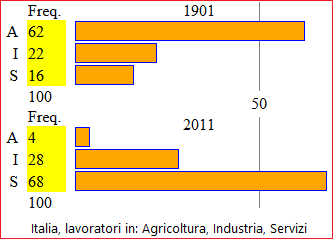
In 1901 agriculture employed more than half of the workers. In 2011, services employed more than half of the workers.

What we have here called the center, mathematicians call the median: it is the class in which the central value falls, ie the one that delimits the first 50% of the data.  Of course, it makes sense to take this into consideration when classes are somehow ordered, such as dice exits, occupational sectors or student performances (that have been evaluated with the letters A, B, ..., F) can be.