Primo esempio:
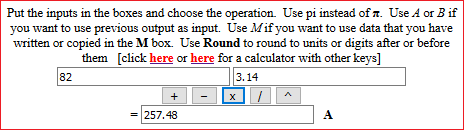
Una ruota ha diametro di 82 cm. Qual è la sua circonferenza?
Un tipico esempio di risposta sbagliata: l'uso di 3.14 e il pensare che 82 cm sia una misura "esatta".

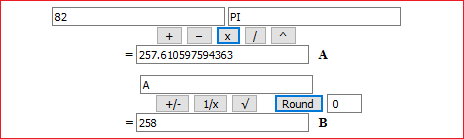
O arrotondare correttamente il risultato (Round "0" arrotonda alle unità), ma poi usare 3.14:

La risposta corretta:
Secondo esempio:
Una classe scolastica in un mese invernale rileva la temperatura esterna in ogni giorno scolastico alle ore 9:
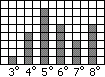
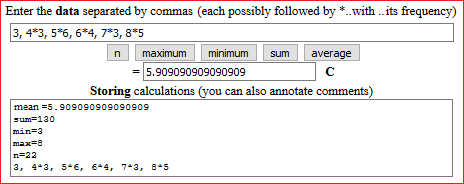
Arrotondo ai decimi:

Terzo esempio:
Diversamente dalle calcolatrici, il computer opera con i numeri in modo tale che i risultati delle operazioni possono differire di alcune unità sull'ultima (la 17ª) cifra.
Comunque fornisce più cifre di quelle usualmente necessarie. Con questa calcolatrice noi possiamo arrotondare i numeri. Qualche esempio.
1 / 3 = 0.3333333333333333
10 / 3 = 3.3333333333333335
3.3333333333333335 round to 14^ digit after units: 3.33333333333333
√3(-8)
-8 ^ 0.3333333333333333 = -1.9999999999999997
-1.9999999999999997 round to 15^ digit after units: -2
Confrontiamo i valori di questi due termini numerici: (19/6177)^2 e (10119/355 - 12398/435)^2.
19 / 6177 = 0.0030759268253197345
0.0030759268253197345 ^ 2 = 0.000009461325834721535
10119 / 355 = 28.504225352112676
12398 / 435 = 28.501149425287355
28.504225352112676 - 28.501149425287355 = 0.003075926825321318
0.003075926825321318 ^ 2 = 0.000009461325834731285
Solo 11 cifre sono uguali mentre i due termini sono equivalenti. Problemi simili ci sono con le usuali calcolatrici.
Vediamo come potremmo verificare l'equivalenza dei due termini:
355 * 435 = 154425
10119 * 435 = 4401765
12398 * 355 = 4401290
4401765 - 4401290 = 475
10119/355 - 12398/435 = 475/154425.
Con questo script posso trovare che:
475/154425 -> 19/6177
Con questo script posso trovare che il periodo di 19/6177 ha 140 cifre:
0.003075926825319734498947709243969564513517888942852517403270195887971
50720414440666990448437752954508661162376558199773352760239598510603853
00307592682531...
Se voglio (e se ho molto tempo a disposizione) posso trovare il periodo di (19/6177)^2 = 361 / 38155329 (è lungo 288250 cifre):
0.000009461325834721540469484616421470248625034788718503777021553136129425066679
41455831765990014134067616085815955092406620317701886412773429368149335050943997
88821110676309461255071342721222506035788605046492981360480471810372805329499321
05158888814718384422789278006225552399246773628920877605327423595272890976775485
28018196357316169387505477937302021429300216491384466898450803556169047841259604
91652424226246352115061044290825011625505836943510564408971548902120592381735196
15045122530590681055325194548840084696950195344928096413478704377047829937464305
44472568956226271826931435973203114039456978604482744730100479542451330979219180
...
Quarto esempio:
843.27−843.23 and 5555.1251−5555:
vedi qui.
Quinto esempio:
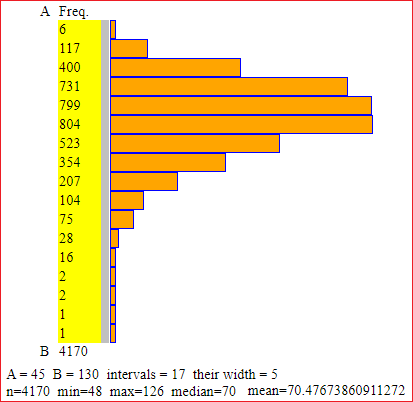
Peso corporeo umano; 4170 maschi italiani ventenni, nel 1990. (vedi).
Abbiamo visto come ottenere il seguente istogramma e le seguenti elaborazioni:
Possiamo ottenere (con questa versione - "pocket calculator-2"):
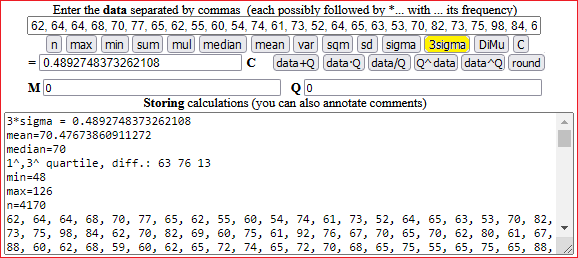
I valori sono arrotondati alle unità. Il 50% centrale dei dati è in [63, 76], un intervallo ampio 13. Il peso medio (dei maschi ventenni italiani, nel 1990) è 70.48±0.49 kg, o 70.5±0.5 kg.
Sesto esempio:
Tra il 2007 e il 2012 l'occupazione ha avuto le seguenti variazioni percentuali (ciascuna calcolata rispetto all'anno precedente): 1.6, 2.8, 1.3, -0.8, 0.9, 1.7. Qual è stata la variazione percentuale complessiva?
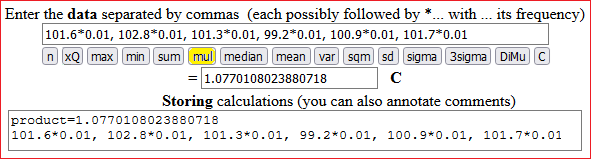
Ottengo 1.077011, o 107.7%: c'è stata una variazione positiva di circa il 7.7%. Ho messo "circa" poiché i dati sono arrotondati e ci possono essere variazioni sull'ultima cifra dovuti all'arrotondamento.
Settimo esempio:
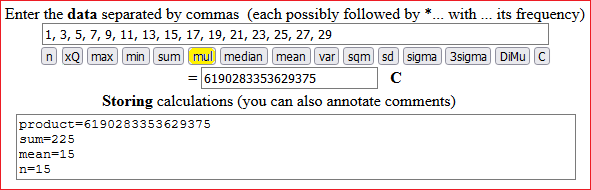
Ottavo esempio:
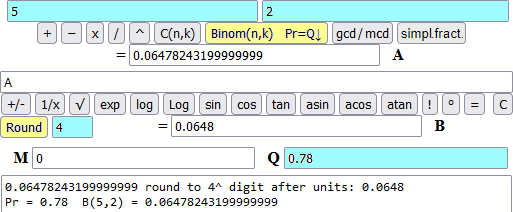
In un gran numero di esperimenti si ottiene che un certo veleno uccide il 78% dei topi su cui è testato. Se utilizzato su un gruppo di 5 topi, qual è la probabilità che 0, 1, 2, 3, 4, 5 topi vengano uccisi?
Pr = 0.78 B(5,5) = 0.28871743680000006 round to 4^ digit after units: 0.2887, 28.87%
Pr = 0.78 B(5,4) = 0.40716561600000006 round to 4^ digit after units: 0.4072, 40.72%
Pr = 0.78 B(5,3) = 0.22968316799999997 round to 4^ digit after units: 0.2297, 22.97%
Pr = 0.78 B(5,2) = 0.06478243199999999 round to 4^ digit after units: 0.0648, 6.48%
Pr = 0.78 B(5,1) = 0.009135983999999998 round to 4^ digit after units: 0.0091, 0.91%
Pr = 0.78 B(5,0) = 0.0005153631999999998 round to 4^ digit after units: 0.0005, 0.05%
Nono esempio:
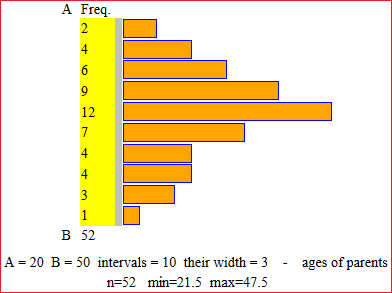
Gli alunni di una classe di quarta elementare raccolgono l'età dei loro genitori quando sono nati. Di seguito sono riportati i dati. Qual era l'età media dei genitori quando sono nati gli alunni?
28, 36, 22, 25, 27, 44, 39, 37, 29, 26, 21, 37, 42, 39, 41, 40, 45, 24, 34, 28, 41, 32, 32, 30, 45, 24, 33, 31, 29, 34, 26, 33, 34, 28, 41, 30, 35, 37, 29, 39, 24, 33, 31, 36, 32, 32, 35, 29, 33, 47, 34, 31
Otteniamo (con questa versione):
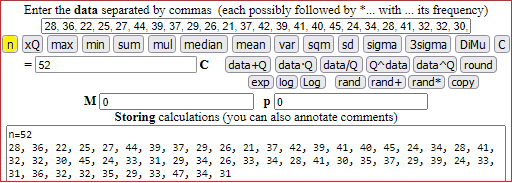
I dati vengono troncati. Per elaborarli correttamente è necessario aggiungere mezzo anno a tutte le età (una persona di 32 anni ha un'età media tra i 32 ei 33 anni).
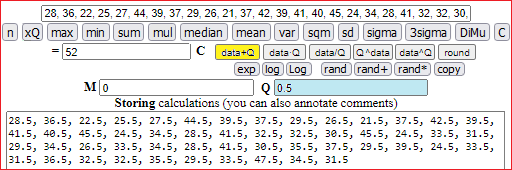
Introduco i dati trasformati. La media è 33.7:

Abbiamo visto come ottenere (con i dati trasformati) il seguente istogramma:
Decimo esempio. L'arrotondamento dovrebbe essere fatto solo alla fine:
In molti manuali, soprattutto in campo biologico, ma anche in campo fisico, tuttora (nel XXI) molti calcoli complessi vengono eseguiti arrotondando i risultati intermedi, perdendo via via informazioni; ma alla fine questi manuali arrotondano il risultato con molte cifre in più rispetto a quelle lecite (una volta, fino alla metà del XX secolo, in assenza di mezzi di calcolo convenienti, si procedeva approssimando i risultati intermedi, ma in genere l'arrotondamento era fatto correttamente ...). Un esempio tratto da un famoso manuale di matematica per le scienze biologiche.
Per valutare la densità degli alberi in un parco vengono contati il numero di alberi per ettaro presenti in 5 aree campione diversamente collocate, ottenendo:
Dimensione in ettari dell'area 1.50, 2.30, 1.75, 3.10, 2.65
Numero di alberi presenti in essa 20, 31, 43, 58, 29
Determina la media e deviazione standard della densità (numero/ettaro).
Sviluppando i calcoli il manuale trova come risposte 16.2 e, quindi, 5.491.
Facciamo i calcoli con la calcolatrice:
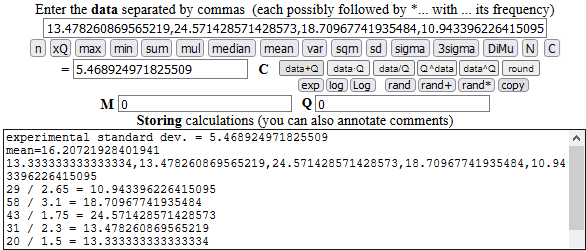
Il valore esteso della deviazione standard sperimentale è 5.468924971825509, il valore arrotondato è 5.469, molto diverso da quello indicato nel manuale (manuale che per fare i calcoli ha usato malamente - e fa utilizzare agli studenti - un costoso software di calcolo numerico!).
Undicesimo esempio. Arrotondare una sequenza di numeri:
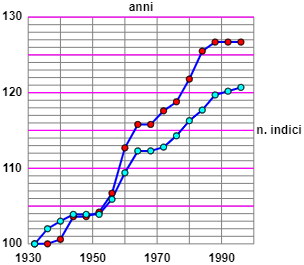
Trasformiamo una sequenza di numeri (ad esempio i record di salto in alto maschile ogni 4 anni dal 1932 al 1996: 203, 207, 209, 211, 211, 211, 215, 222, 228, 228, 229, 232, 236, 239, 243, 244, 245) in numeri indici (poniamo uguale a 100 il primo dato e trasformiamo proporzionalmente gli altri) e poi arrotondiamo i numeri indici alla seconda cifra dopo il ".".
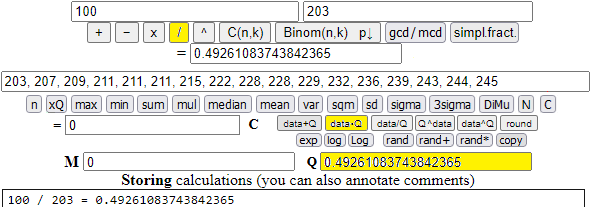
Ho messo la sequenza dei dati (separati da ",") nel box "data". Ho calcolato 100/203. Ho copiato l'esito nel box Q. Quindi ho cliccato [data·Q].

Con [C] cancello i "data", copio e incollo al loro posto i numeri indici ottenuti e, infine, metto 2 a fianco a [Round] e clicco [round]:
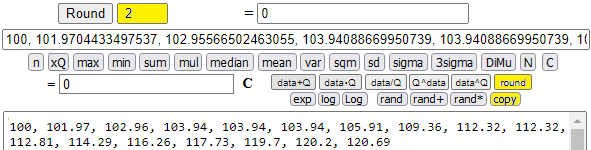
Se trasformo in modo simile i dati sui record femminili (165, 165, 166, 171, 171, 172, 176, 186, 191, 191, 194, 196, 201, 207, 209, 209, 209) e rappresento tutto graficamente (utilizzando questo script) ottengo:
Dodicesimo esempio. Introdurre espressioni invece che numeri.
Posso introdurre nelle celle invece che singoli numeri termini che contengono più numeri (le uniche operazioni ammesse sono +, *, -, / e quelle del tipo "Math" - vedi sotto).



| 36 + 1 |
| ————— |
| 53 · 24 · 0.3 |


Usable "Math" Functions:
abs(a) / |a| log10(a) / log of a base 10
acos(a) / arc cosine of a max(a,b)
asin(a) / arc sine of a min(a,b)
atan(a) / arc tangent of a pow(a,b) / a to the power b
atan2(a,b) / arc tangent of a/b random() / random n. in [0,1)
cbrt(a) / cube root of a round(a) / integer closest to a
ceil(a) / integer closest to a not < a sign(a) / sign of a
cos(a) / cosine of a sin(a) / sine of a
exp(a) / exponential of a sqrt(a) / square root of a
floor(a) / integer closest to a not > a tan(a) / tangent of a
log(a) / log of a base e trunc(a) / integer portion of a
log2(a) / log of a base 2 PI / π
cosh(a),sinh(a),tanh(a), acosh(a),asinh(a),atanh(a) hyperbolic functions
Note: M%%N is the remainder of M/N, != is "not equal"
|
Altri esempi:

cbrt(27000) output: 30
max(39/7, 6, 79/14) output: 6
random() output: 0.9055236689456472
random() output: 0.8572220665948553
random() output: 0.16923464144969635
Il lancio di due dadi equi:
trunc(random()*6+random()*6)+2 output: 4
trunc(random()*6+random()*6)+2 output: 8
trunc(random()*6+random()*6)+2 output: 6
trunc(random()*6+random()*6)+2 output: 9
trunc(random()*6+random()*6)+2 output: 11
Tredicesimo esempio. Potenze a base negativa
5 [^] -2 -> 0.04 -5 [^] -2 -> 0.04 -5 [^] -3 -> -0.008 5 [^] -3 -> 0.008 125 [^] 1/3 -> 5 125 [^] -1/3 -> 0.2 -2 [^] -1/3 -> NaN 1 dispari -2 ^ (-1/3) = -2 ^ -1 ^ (1/3) = (-1/2) ^ (1/3) 1/2 [^] 1/3 -> 0.7937005259840998 [+/-] 0.7937005259840998 -> -0.7937005259840998 -2 [^] -4/3 -> NaN 4 pari -2 ^ (-4/3) = -2 ^ -1 ^ (4/3) = (-1/2) ^ (4/3) = (1/2) ^ (4/3) 1/2 [^] 4/3 -> 0.3968502629920499 (-5/3)^(-5/3) = (-5/3)^(-1)^(5/3) = (-3/5)^(5/3) = -(3/5)^(5/3) = -0.426827... 5 dispari (-2/3)^(-2/3) = (-2/3)^(-1)^(2/3) = (-3/2)^(2/3) = (3/2)^(2/3) = 1.31037... 2 pari (-2)^(-1/4), (-5/2)^(-5/2), (-a)^(m/n) [-a negativo, m/n semplificata, n pari] non sono definiti WolframAlpha (-2)^(-1/3) (scegli "Use the real valued root") = -2^(2/3)/2 = -0.7937005... (-5/2)^(-5/2) (non posso scegliere "Use the real valued root")
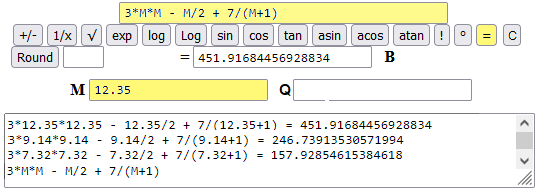
Quattordicesimo esempio. Uso di M (e delle altre "lettere")
Il valore collocato in M può essere usato nelle finestre di input (sia quelle a 2 input che quella a 1 input) usando la lettera M (che viene automaticamente trasformata nel valore che rappresenta). Nella finestra ad 1 input può M essere impiegata anche all'interno di un termine più complesso; un esempio (scrivo il termine "3*M*M - M/2 + 7/(M+1)" nella finestra in basso così da poterlo copiare):
Analogamente posso impiegare Q, A e B. Esempio: studio di lim x → 0 cos(sin(1/x)*x). Metto la funzione in Q indicando la variabile con M e mettendone man mano i valori in [M]:

M = 1e-8 1 [leggi dal basso in alto]
M = 1e-7 0.9999999999999991
M = 1e-6 0.9999999999999387
M = 1e-5 0.999999999999936
M = 1e-4 0.9999999995329992
M = 1e-3 0.9999996581351323
M = 1e-2 0.9999871797192685
M = 1e-1 0.9985205700839945
M = 1 0.6663667453928805
cos(sin(1/M)*M) [← lo metto in Q e poi via via scrivo Q come input]
Altro esempio: la derivata di x³+1 in 4 (metto in Q il rapporto incrementale usando M come dx, e poi via via scrivo Q come input)

M = 1e-4 48.00120000993502
M = 1e-3 48.01200100001779
M = 1e-2 48.120099999998445
M = 1e-1 49.20999999999978
Ovvero con "( pow(4+M,3)+1) - pow(4-M,3)-1) / (M*2)":
M = 1e-3 48.000001000005454
M = 1e-1 48.00999999999991
Altro esempio: la successione definita ricorsivamente P(0) = 1, P(n+1) = P(n)*1.5.
Metti 1 in B, B*1.5 in M.
Metti M nel box sotto ad A. Clicca [=] [=] e nota che cosa appare in B.
Metti M nel box sotto ad A. Clicca [=] [=] e nota che cosa appare in B.
...
Ottieni via via in B:
1 1.5 2.25 3.375 5.0625 7.59375 11.390625 ...
Quindicesimo esempio. Uso dei numeri interi
Per attività di vario tipo possono essere utili sequenze iniziali dei numeri interi positivi. In fondo puoi recuperarli. Un esempio. La somma, la media e la mediana dei quadrati dei primi 100 numeri interi positivi:
Metto nei "data" i primi 100 numeri:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100
Cliccando "data^2" ottengo:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, 2601, 2704, 2809, 2916, 3025, 3136, 3249, 3364, 3481, 3600, 3721, 3844, 3969, 4096, 4225, 4356, 4489, 4624, 4761, 4900, 5041, 5184, 5329, 5476, 5625, 5776, 5929, 6084, 6241, 6400, 6561, 6724, 6889, 7056, 7225, 7396, 7569, 7744, 7921, 8100, 8281, 8464, 8649, 8836, 9025, 9216, 9409, 9604, 9801, 10000
Copio questi valori nei "data" e clicco "sum", "mean", "median"
sum = 338350 mean=3383.5 median=2500
1 - 1000
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314, 315, 316, 317, 318, 319, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329, 330, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 343, 344, 345, 346, 347, 348, 349, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359, 360, 361, 362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377, 378, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, 392, 393, 394, 395, 396, 397, 398, 399, 400, 401, 402, 403, 404, 405, 406, 407, 408, 409, 410, 411, 412, 413, 414, 415, 416, 417, 418, 419, 420, 421, 422, 423, 424, 425, 426, 427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439, 440, 441, 442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452, 453, 454, 455, 456, 457, 458, 459, 460, 461, 462, 463, 464, 465, 466, 467, 468, 469, 470, 471, 472, 473, 474, 475, 476, 477, 478, 479, 480, 481, 482, 483, 484, 485, 486, 487, 488, 489, 490, 491, 492, 493, 494, 495, 496, 497, 498, 499, 500, 501, 502, 503, 504, 505, 506, 507, 508, 509, 510, 511, 512, 513, 514, 515, 516, 517, 518, 519, 520, 521, 522, 523, 524, 525, 526, 527, 528, 529, 530, 531, 532, 533, 534, 535, 536, 537, 538, 539, 540, 541, 542, 543, 544, 545, 546, 547, 548, 549, 550, 551, 552, 553, 554, 555, 556, 557, 558, 559, 560, 561, 562, 563, 564, 565, 566, 567, 568, 569, 570, 571, 572, 573, 574, 575, 576, 577, 578, 579, 580, 581, 582, 583, 584, 585, 586, 587, 588, 589, 590, 591, 592, 593, 594, 595, 596, 597, 598, 599, 600, 601, 602, 603, 604, 605, 606, 607, 608, 609, 610, 611, 612, 613, 614, 615, 616, 617, 618, 619, 620, 621, 622, 623, 624, 625, 626, 627, 628, 629, 630, 631, 632, 633, 634, 635, 636, 637, 638, 639, 640, 641, 642, 643, 644, 645, 646, 647, 648, 649, 650, 651, 652, 653, 654, 655, 656, 657, 658, 659, 660, 661, 662, 663, 664, 665, 666, 667, 668, 669, 670, 671, 672, 673, 674, 675, 676, 677, 678, 679, 680, 681, 682, 683, 684, 685, 686, 687, 688, 689, 690, 691, 692, 693, 694, 695, 696, 697, 698, 699, 700, 701, 702, 703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713, 714, 715, 716, 717, 718, 719, 720, 721, 722, 723, 724, 725, 726, 727, 728, 729, 730, 731, 732, 733, 734, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745, 746, 747, 748, 749, 750, 751, 752, 753, 754, 755, 756, 757, 758, 759, 760, 761, 762, 763, 764, 765, 766, 767, 768, 769, 770, 771, 772, 773, 774, 775, 776, 777, 778, 779, 780, 781, 782, 783, 784, 785, 786, 787, 788, 789, 790, 791, 792, 793, 794, 795, 796, 797, 798, 799, 800, 801, 802, 803, 804, 805, 806, 807, 808, 809, 810, 811, 812, 813, 814, 815, 816, 817, 818, 819, 820, 821, 822, 823, 824, 825, 826, 827, 828, 829, 830, 831, 832, 833, 834, 835, 836, 837, 838, 839, 840, 841, 842, 843, 844, 845, 846, 847, 848, 849, 850, 851, 852, 853, 854, 855, 856, 857, 858, 859, 860, 861, 862, 863, 864, 865, 866, 867, 868, 869, 870, 871, 872, 873, 874, 875, 876, 877, 878, 879, 880, 881, 882, 883, 884, 885, 886, 887, 888, 889, 890, 891, 892, 893, 894, 895, 896, 897, 898, 899, 900, 901, 902, 903, 904, 905, 906, 907, 908, 909, 910, 911, 912, 913, 914, 915, 916, 917, 918, 919, 920, 921, 922, 923, 924, 925, 926, 927, 928, 929, 930, 931, 932, 933, 934, 935, 936, 937, 938, 939, 940, 941, 942, 943, 944, 945, 946, 947, 948, 949, 950, 951, 952, 953, 954, 955, 956, 957, 958, 959, 960, 961, 962, 963, 964, 965, 966, 967, 968, 969, 970, 971, 972, 973, 974, 975, 976, 977, 978, 979, 980, 981, 982, 983, 984, 985, 986, 987, 988, 989, 990, 991, 992, 993, 994, 995, 996, 997, 998, 999, 1000
Sedicesimo esempio. Cifre visualizzate
I risultati di una operazione vengono arrottondati a 17 cifre ma l'ultima cifra non e' attendibile. Conviene (eventualmente usando Round) arrotondare a meno cifre, come del resto occorre fare in tutti i contesti:
asin(0.5) = 0.5235987755982989 = 30.000000000000004 ^ 6 / 8 produce 0.75 0.6 / 0.8 produce 0.7499999999999999
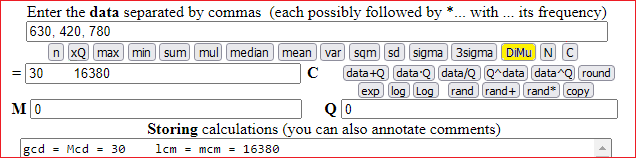
Diciassettesimo esempio. Massimo comune divisore / Minimo comune multiplo
Il tasto [DiMu] stampa il massimo comune divisore (greatest common divisor) e il minimo comune multiplo (least common multiple) di una sequenza di numeri interi positivi.