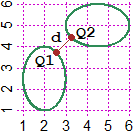
First example  (that I can also study with the script for the distance between 2 ellipses) The distance between the curve x=cos(t)+2, y=sin(t)*1.5+2.5 and the curve x=cos(t)*1.5+4.5, y=sin(t)+5: distance = 0.986024149 nearest point2 of the curves: (2.554700, 3.748075), (3.251925, 4.4452998)

function x1(t) { with(Math) {
return  cos(t)+2
}}
function y1(t) { with(Math) {
return  sin(t)*1.5+2.5
}}
function x2(t) { with(Math) {
return  cos(t)*1.5+4.5
}}
function y2(t) { with(Math) {
return  sin(t)*1+5
}}

 

We can draw the graph with JavaScript; for example, see the script curve_curve  (see the code;  se also here).

Moreover, the graph can be drawn, as well as with R, with Desmos:

 

Other curves The distance between  y = x²  and  x = cos(t)+2, y = sin(t)*1.5-2.5: distance = 1.74943908401 nearest point2 of the curves: (1.520061, -1.184047), (0.410297, 0.1683436)

function x1(t) { with(Math) {
return  t
}}
function y1(t) { with(Math) {
return  pow(t,2)
}}
function x2(t) { with(Math) {
return  cos(t)+2
}}
function y2(t) { with(Math) {
return  sin(t)*1.5-2.5
}}
d = 1.7494390840149902  t1 = 0.41029702324367284  t2 = 2.0713815877036205
Q1: 0.41029702324367284,0.16834364728261902  Q2: 1.520060928766358,-1.1840472661289747
  a1,b1: 0.41029,0.4103  a2,b2: 2.0713,2.0714
d = 1.7494390840150015  t1 = 0.4102970454827357  t2 = 2.0713816899039496
Q1: 0.4102970454827357,0.16834366553186208  Q2: 1.5200608391058256,-1.184047339703878
  a1,b1: 0.4102,0.4103  a2,b2: 2.071,2.072
d = 1.749439084691748  t1 = 0.41028668402882107  t2 = 2.0714091751288546
Q1: 0.41028668402882107,0.16833516309136565  Q2: 1.5200367264505558,-1.1840671270546023
  a1,b1: 0.405,0.415  a2,b2: 2,2.1
d = 1.7494390851059962  t1 = 0.4102815903498466  t2 = 2.0714163627364996
Q1: 0.4102815903498466,0.16833098337999935  Q2: 1.520030420856835,-1.1840723017701355
  a1,b1: 0.35,0.45  a2,b2: 1.8,2.2
d = 1.7494391666857405  t1 = 0.4105189163597722  t2 = 2.071121855292903
Q1: 0.4105189163597722,0.16852578068920165  Q2: 1.5202888086696688,-1.1838603269208176
  a1,b1: 0,5  a2,b2: 0,6.28

Other curves The distance between  y = x/2;  and  x = cos(t)+2, y = sin(t)*1.5-2.5: distance = 1.71628160613 nearest point2 of the curves: (0.9162278, 0.4581139), (1.6837722, -1.0769750)

function x1(t) { with(Math) {
return  t
}}
function y1(t) { with(Math) {
return  t/2
}}
function x2(t) { with(Math) {
return  cos(t)+2
}}
function y2(t) { with(Math) {
return  sin(t)*1.5-2.5
}}
d = 1.7162816061266104  t1 = 0.9162277661823271  t2 = 1.8925468740338862
Q1: 0.9162277661823271,0.4581138830911636  Q2: 1.6837722407735076,-1.0769750495290564
  a1,b1: 0.91622,0.91623  a2,b2: 1.89254,1.89255
d = 1.7162816061266106  t1 = 0.9162277629298269  t2 = 1.892546883010431
Q1: 0.9162277629298269,0.45811388146491344  Q2: 1.6837722322576094,-1.0769750537870057
  a1,b1: 0.9162,0.9163  a2,b2: 1.8925,1.8926
d = 1.7162816061304648  t1 = 0.9162238576869414  t2 = 1.8925479585265916
Q1: 0.9162238576869414,0.4581119288434707  Q2: 1.6837712119335746,-1.0769755639499405
  a1,b1: 0.91,0.92  a2,b2: 1.89,1.9
d = 1.7162816116011616  t1 = 0.9161148453240433  t2 = 1.892537416791737
Q1: 0.9161148453240433,0.45805742266202165  Q2: 1.6837812127153428,-1.076970563628954
  a1,b1: 0.8,1  a2,b2: 1.8,2
d = 1.7162829284602516  t1 = 0.9184100143789129  t2 = 1.8921826600372027
Q1: 0.9184100143789129,0.45920500718945645  Q2: 1.6841177854763587,-1.0768023820522356
  a1,b1: -1,3  a2,b2: 0,6.28

Other curves The distance between  y² = 4·x;  and the circle whose center is (6,0) and radius is √5. Or:  between  x = y²/4  and  x = cos(t)·√5+6, y = sin(t)·√5: distance = √5 nearest points of the curves:  (4, 4), (5, 2), or:  (4, -4), (5, -2)

function x1(t) { with(Math) {
return  pow(t,2)/4
}}
function y1(t) { with(Math) {
return  t
}}
function x2(t) { with(Math) {
return  cos(t)*sqrt(5)+6
}}
function y2(t) { with(Math) {
return  sin(t)*sqrt(5)
}}
d = 2.2360679774997893  t1 = 4  t2 = 2.034443942014127
Q1: 4,4  Q2: 4.999999987563151,1.9999999937815757
  a1,b1: 4,4  a2,b2: 2.03444,2.03445
d = 2.2360679774997893  t1 = 4  t2 = 2.034443944439723
Q1: 4,4  Q2: 4.99999998271196,1.99999999135598
  a1,b1: 4,4  a2,b2: 2.034,2.035
d = 2.23606797749979  t1 = 4  t2 = 2.034443922597264
Q1: 4,4  Q2: 5.000000026396878,2.000000013198439
  a1,b1: 4,4  a2,b2: 2,2.1
d = 2.236067984081465  t1 = 3.9999248114594516  t2 = 2.0345241064510655
Q1: 3.9998496243322323,3.9999248114594516  Q2: 4.999839661903113,1.9999198229173891
  a1,b1: 3.9,4.1  a2,b2: 1.9,2.1
d = 2.23607357581484  t1 = 3.999332297031233  t2 = 2.0332239002674015
Q1: 3.998664705519279,3.999332297031233  Q2: 5.00244081469452,2.001218546739128
  a1,b1: 0,10  a2,b2: 0,6.28

Other curves The distance between  y = x+10;  and the parabola  y² = 36·x  (x = y²/36): distance = √2/2 nearest points of the curves:  (8.5, 18.5), (9, 18)

function x1(t) { with(Math) {
return  t
}}
function y1(t) { with(Math) {
return  t+10
}}
function x2(t) { with(Math) {
return  pow(t,2)/36
}}
function y2(t) { with(Math) {
return  t
}}
d = 0.7071067811865476  t1 = 8.5  t2 = 18
Q1: 8.5,18.5  Q2: 9,18
  a1,b1: 8.5,8.5  a2,b2: 18,18
d = 0.707106782444305  t1 = 8.50006113808483  t2 = 18.000031548471813
Q1: 8.50006113808483,18.50006113808483  Q2: 9.00003154849946,18.000031548471813
  a1,b1: 8.4,8.6  a2,b2: 17.9,18.1
d = 0.7071068277279571  t1 = 8.500758554813238  t2 = 18.000905266627672
Q1: 8.500758554813238,18.50075855481324  Q2: 9.000905289391774,18.000905266627672
  a1,b1: 8,9  a2,b2: 17,19
d = 0.7071068199893746  t1 = 8.498598716340616  t2 = 17.998640926050758
Q1: 8.498598716340616,18.498598716340616  Q2: 8.99864097735859,17.998640926050758
  a1,b1: 5,10  a2,b2: 10,20
d = 0.7071296055077205  t1 = 8.482876301283491  t2 = 17.986566077927918
Q1: 8.482876301283491,18.48287630128349  Q2: 8.986571090990757,17.986566077927918
  a1,b1: -5,20  a2,b2: 0,25