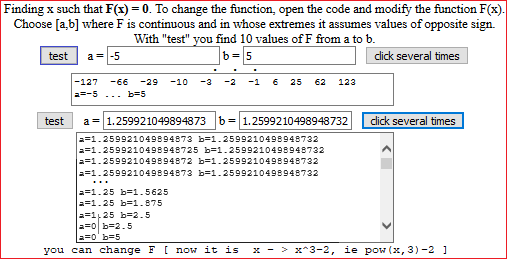
• At the beginning the function is  F: x → x^3−2, that I could study with this program, for polynomial functions.
   Alternatively, I can use pocket calculator directly.

function F(x) {
with(Math) {
/// you can change F [ now it is  x - > x^3-2, ie pow(x,3)-2 ]

return pow(x,3)-2

}}

We know that the solution is 2^1/3 = 1.259921049894873…. With the present script I find:

• Another example:  we solve for x the equation  sin(x) = x² - x + 1/2.

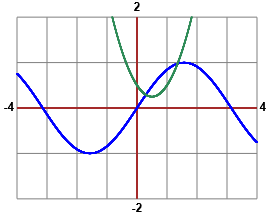
We can draw the graphs with JavaScript; for example, see the script fun00_equ.htm

function F(x) {
with(Math) {
return sin(x)-(x*x-x+1/2)
}}

a=0.29594100248899996 b=0.295941002489
...
a=0.28125 b=0.3125
a=0.25 b=0.3125
a=0.25 b=0.375
a=0.25 b=0.5
a=0 b=0.5
a=0 b=1

a=1.3521717451122257 b=1.352171745112226
...
a=1.34375 b=1.375
a=1.3125 b=1.375
a=1.25 b=1.375
a=1.25 b=1.5
a=1 b=1.5
a=1 b=2

2 solutions:    0.295941002489     1.352171745112