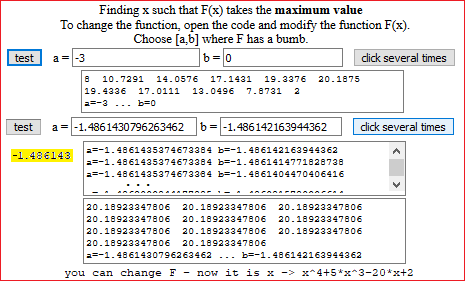
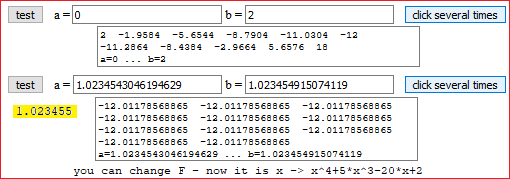
• At the beginning the function is  F: x → x^4+5*x^3-20*x+2, that I could study with this program, for polynomial functions.
   Alternatively, I can use pocket calculator directly.

function F(x) {
with(Math) {
/// you can change F [ now it is  x - > x^4+5*x^3-20*x+2, ie pow(x,4)+5*pow(x,3)-20*x+2 ]

y = pow(x,4)+5*pow(x,3)-20*x+2
return y

}}

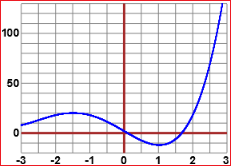
Maximum between -3 and 0:

Minimum between 0 and 2:

For graphs see here.

• To consider another function, we study F: x → x³·cos(x)/( (cos(x)+x)·(sin(x)−x) ) in the interval [0.5, 5].

function F(x) {
with(Math) {

y = pow(x,3)*cos(x) / (  (cos(x)+x)*( sin(x)-x ) )
return y

}}

In x=0, where sin(x)-x = 0, it is not defined. It is continuous function in [-1/2,0) ∪ (0,5]. How can we fill the hole in order to obtain a continuous function in [-1/2,5]? We calculate lim _{x → 0} F(x). We can use this script (to tabulate the function), with the new F:

function F(x) { with(Math) {
y = pow(x,3)*cos(x) / (  (cos(x)+x)*( sin(x)-x ) )
return y
}}

We could thicken the tab, but it is "evident" that the limit is 6.

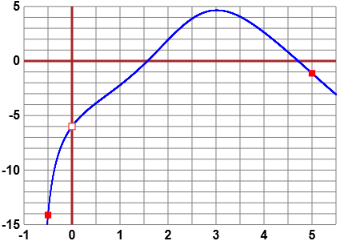
Let's look for the "maximum" of F. With this program (with the new F) I find:

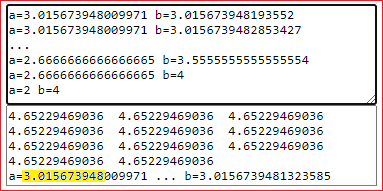
F has the maximum value 4.65229469036 at 3.015673948.