First example. function x(t) { with(Math) { return t }} function y(t) { with(Math) { return sin(t) }} If I put n=1e4, a=-PI, b=PI I have 7.640395538638171. Then I get the above values. I can take:   lenght = 7.64039557806

If I change x(t), y(t) I can If consider any curve.

Second example.
function x(t) { with(Math) {
return cos(t)*172/2
}}
function y(t) { with(Math) {
return sin(t)*136/2
}}
a = 0,  b = 2PI

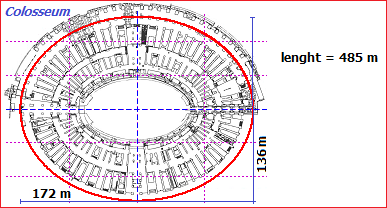
I can take:  lenght = 485 m:

We can draw the graph with JavaScript; for example, see the script colosseum  (see the code;  se also here).

Third example.
A wire stretched between two pylons 50 meters apart has the shape of the catenary y = K/2*(exp(x/K)+exp(-x/K)) with K = 100 (m). What is the length of the wire?

function x(t) { with(Math) {
return  t
}}
function y(t) { with(Math) {
K = 100;
return  K/2*(exp(t/K)+exp(-t/K))
}}
50.52246336163236  if a=-25 b=25 n=64e4 [1.9113599591946695e-11]
50.52246336161325  if a=-25 b=25 n=16e4 [3.015969696207321e-10]
50.52246336131165  if a=-25 b=25 n=4e4 [4.83302642351191e-9]
50.522463356478625  if a=-25 b=25 n=1e4 [50.522463356478625]

Rounding, 50.52 m.

Fourth example.
Let us consider the curve in polar coordinates  ρ = sin(θ/2)³, θ in [0, 4π). What is its length?
ρ = f(θ)   →   x = f(θ)·cos(θ), y = f(θ)·sin(θ).

function x(t) { with(Math) {
return  pow(sin(t/2),3)*cos(t)
}}
function y(t) { with(Math) {
return  pow(sin(t/2),3)*sin(t)
}}

7.151268506842977  if a=0 b=12.566370614359172 n=1024e4 [1.7691625942006795e-11]
7.151268506825286  if a=0 b=12.566370614359172 n=256e4  [2.7280133707563436e-10]
7.151268506552484  if a=0 b=12.566370614359172 n=64e4   [4.3619552414497775e-9]
7.151268502190529  if a=0 b=12.566370614359172 n=16e4   [6.97931170634547e-8]
7.151268432397412  if a=0 b=12.566370614359172 n=4e4    [0.0000011166891162872616]
7.151267315708296  if a=0 b=12.566370614359172 n=1e4    [7.151267315708296]

7.15126850684

We can draw the graph with JavaScript; for example, see the script polar  (see the code;  se also here).