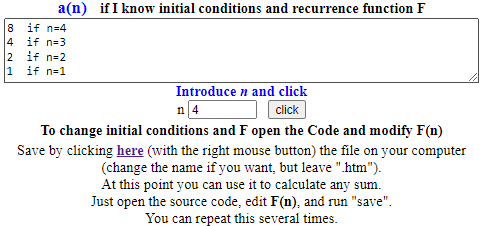
It can be used also the "pocket calculator": see down.

• recursion - A     F(1) = 1, F(n+1) = 2·F(n)

function F(n) {
with(Math) {
a = 1; for(i=2; i<=n; i++) {a = 2*a}
return a
}}

• recursion - B     F(1) = 1, F(n+1) = (F(n) + K/F(n)) / 2, K=2     A sequence that tends to √2.

function F(n) {
with(Math) {
a = 1; for(i=2; i<=n; i++) { a = (a+2/a)/2 }
return a
}}

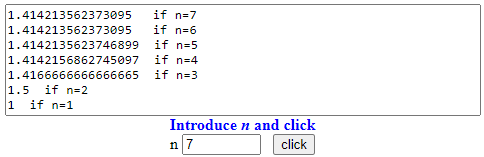
• recursion - B1     F(1) = 1, F(n+1) = (F(n) + K/F(n)) / 2, K=16     A sequence that tends to √16 = 4.

function F(n) {
with(Math) {
a = 1; for(i=2; i<=n; i++) { a = (a+16/a)/2 }
return a
}}

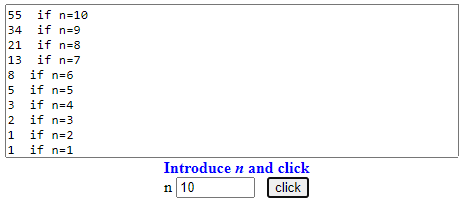
• recursion - C     F(1)=1, F(2)=1, F(n+2) = F(n)+F(n+1)     The Fibonacci sequence, such that each number is the sum of the two preceding ones:

function F(n) {
with(Math) {
a = 1; b = 1; for(i=3; i<=n; i++) {A = a; a = a+b; b = A }
return a
}}

• recursion - D     How to study  1² + 2² + 3² + ... + n² ?.

function F(n) {
with(Math) {
a = 1; for(i=2; i<=n; i++) {a = a + pow(i,2) }
return a
}}

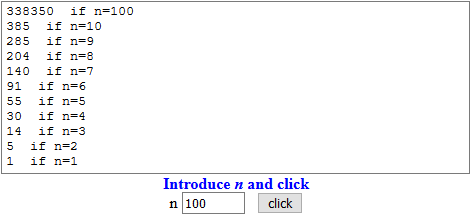
It can be shown that 1² + 2² + 3² + ... + n² = n·(n+1)·(2n+1)/6.

• recursion - E     How to study  F(n) = Σ _{k = 1 .. 2·n} (−1)^k·(2·k + 1) ? Is F(n) proportional to n?

function F(n) {
with(Math) {
m=2*n
a = 0; for(i=1; i<=m; i++) {a = a+pow(-1,i)*(2*i+1)}
return a
}}

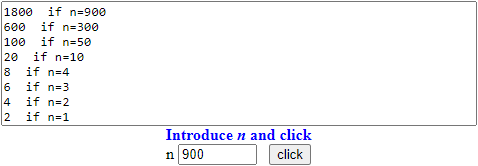
F(n) = 2·n.

• See also "square root" and "cube root".

• It can be use also the pocket calculator:
es. B1. I put K in A,  F(1) in B,  (B + A/B)/2 in the box and click [=], [=], [=], ...

(1+16/1)/2 = 8.5
(8.5+16/8.5)/2 = 5.1911764705882355
(5.1911764705882355+16/5.1911764705882355)/2 = 4.136664722546242
(4.136664722546242+16/4.136664722546242)/2 = 4.002257524798522
(4.002257524798522+16/4.002257524798522)/2 = 4.000000636692939
(4.000000636692939+16/4.000000636692939)/2 = 4.000000000000051
(4.000000000000051+16/4.000000000000051)/2 = 4

1+1 = 2
1+2 = 3
2+3 = 5
3+5 = 8
5+8 = 13
...