Simple tabulations for each function can be done with WolframAlpha:  see.

They can also be done with pocket calculator:  see.

• At the beginning  F(x) = sin(x)/x  is calculated.

function F(x) { with(Math) {
y = sin(x)/x
return y
}}

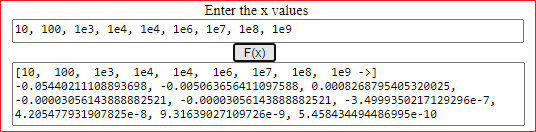
For example, I can deduce that, as x → 0, sin(x)/x → 1:

and that, as x → ∞, sin(x)/x → 0:

 

• (tan(x)-sin(x)+1-cos(x)) / (x*x+1-cos(x))  as  x → 0

function F(x) { with(Math) {
y = (tan(x)-sin(x)+1-cos(x)) / (x*x+1-cos(x))
return y
}}

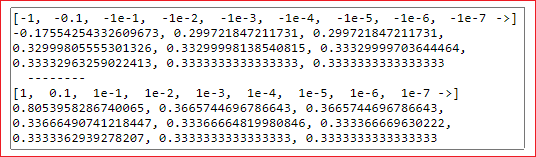
The limit is 1/3.

• √(x*x+x)-√(x*x-2)  as  x → ∞

function F(n) {
with(Math) {
y = sqrt(x*x+x)-sqrt(x*x-2)
return y
}}

The limit is 1/2.

• n / (n!)^1/n  as  n → ∞

function F(x) { with(Math) {
 y = x / pow(Fat(x), 1/x)
 return y
}}

function Fat(n) { with(Math) {
 y = 1; for (k=1; k <= n; k++) {y = y*k}
 return y
}}

 [170,  171,  172,  173,  174,  175 ->]
 2.663087878748024, 0, 0, 0, 0, 0
   --------
 [150,  160,  170,  180,  190 ->]
 2.6569209686814057, 2.660179125103347, 2.663087878748024, 0, 0
   --------
 [1,  50,  100,  150,  200 ->]
 1, 2.5663063992029507, 2.6320853228463696, 2.6569209686814057, 0

171 → 0  because (for computer)  171! = infinity  (170! = 7.257415615307994e+306).  F(170) = 2.663087878748024.  It can be proven that (as N → ∞) F(N) → e = 2.71828182...

• F(x) = sin(x)−tan(x) as x → 0.  Limit is 0. With which order F(x) tends to 0?

function F(n) {
with(Math) {
y = sin(x)-tan(x)
return y
}}

 [1e-1,  1e-2,  1e-3,  1e-4,  1e-5  -> ]
 -0.0005012554386223944, -5.00012500542768e-7, -5.000001250705932e-10, -4.999999980020986e-13, -5.000001606324245e-16

If x is divided by 10, F(x) is divided by 1000. F(x) is an infinitesimal of order 3.

sin(x)-tan(x) ≈ Q·x³.  Q = ?

I study the limit of (sin(x)-tan(x))/x³:

function F(x) { with(Math) {
 y = (sin(x)-tan(x))/pow(x,3)
 return y
}}

 [1e-1, 1e-2, 1e-3, 1e-4, 1e-5 ->]
 -0.5012554386223943, -0.5000125005427679, -0.5000001250705932, -0.4999999980020986, -0.5000001606324244

I can deduce that Q = −1/2, that is, that (as x → 0) sin(x)-tan(x) ≈ −1/2·x³.

function F(x) { with(Math) {
 k = 2
 y = log(1+x*x)/sin(pow(x,k))
 return y
}}