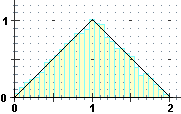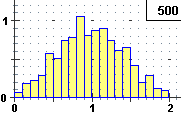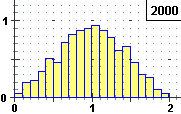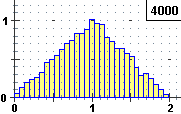
• X+Y < K,  if  X, Y ∈ [0,1].   If  K = 0.75  I have:

Why  Pr(X+Y < 0.75) = 0.28125?  Why  Pr(X+Y < 1) = 0.5?  ...

     

I can represent the distribution of X + Y with rnd+rnd  (rndPrnd in italiano), rndrnd with the numerical outputs:


 

• With xy we evaluate the probability that - if X and Y are random numbers uniformly distributed in [0,1) - X*Y < 1/2:

We take X and Y numbers at random between 0 and 1.
We evaluate the probability that X*Y < K (0<K<1; write K in full, not as a fraction)
K = 0.5   n. tries = 16384e5   84.65836737061%
K = 0.5   n. tries = 8192e5    84.6600970459%
K = 0.5   n. tries = 4096e5    84.65567675781%
K = 0.5   n. tries = 2048e5    84.65673828125%
K = 0.5   n. tries = 1024e5    84.65756054688%
K = 0.5   n. tries = 512e5     84.6545078125%
K = 0.5   n. tries = 256e5     84.6526953125%
K = 0.5   n. tries = 128e5     84.657828125%
K = 0.5   n. tries = 64e5      84.651984375%
K = 0.5   n. tries = 32e5      84.65771875%
K = 0.5   n. tries = 16e5      84.666875%
K = 0.5   n. tries = 8e5       84.579625%
K = 0.5   n. tries = 4e5       84.644%
K = 0.5   n. tries = 2e5       84.564%
K = 0.5   n. tries = 1e5       84.398%

The probability is 84.66. With 107 tries and K = 0.05, 0.1, 0.2, ..., 0.9 I obtain values which I can represent with:

• The random numbers are obtained with the function random() (in JS script; in other languages it can have different names), that produces a number taken at random (apparently - the number is generated by an algorithm) with uniform distribution in [0,1). Here the distribution, obtained with rnd: