Cognome Nome

________________________________

classe

__________________

La matematica dei cambiamenti - Scheda 3

1. Riepilogo

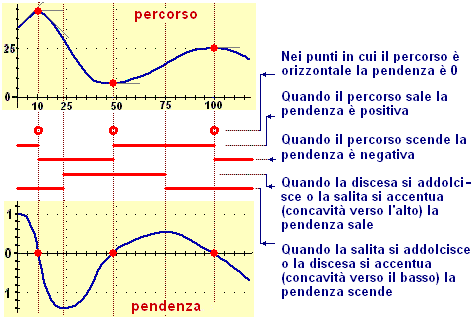
In un tratto di strada con la concavità verso il basso, come un dosso, la pendenza scende:  è positiva lungo la salita; poi diventa zero alla fine di essa e negativa quando comincia la discesa.  Lungo una cunetta, che ha la concavità verso l'alto, la pendenza invece sale:  è negativa nella discesa iniziale; diventa zero e poi positiva, in salita.  Ecco il grafico della pendenza nel caso di un percorso sulle montagne russe:

Si è visto che considerazioni simili valgono anche per il grafico di una funzione, e ci si è posti il problema, nota una formula per esso, di ricavare una formula per il grafico della sua pendenza.

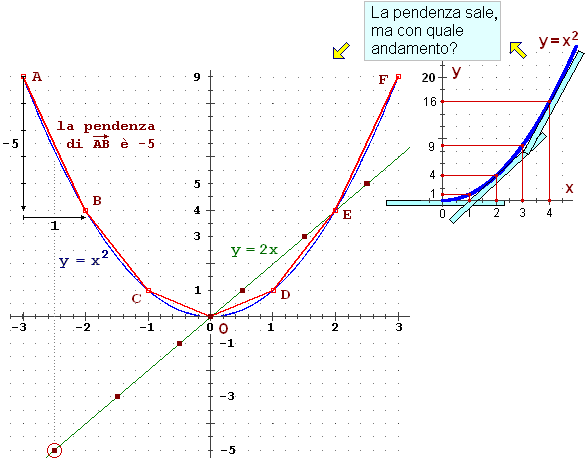
Siamo partiti dal grafico di equazione y = x², che ha pendenza via via crescente, e abbiamo cercato di calcolare la pendenza approssimando il grafico con dei tratti rettilinei, come richiamato nella figura precedente:
• passando da A a B la ascissa varia di 1 e l'ordinata di −5,
• quindi la pendenza è −5/1 = −5;
• abbiamo segnato sul sistema di riferimento in corrispondenza dell'ascissa −2.5, che sta a metà tra A e B, il punto di ordinata −5;
• abbiamo fatto la stessa cosa per gli altri tratti di grafico (da B a C, da C a O, …).
In pratica abbiamo preso come pendenza in -2.5, -1.5, ..., 2.5 quella di opportuni segmenti che approssimano il grafico attorno a tali ascisse.
    Abbiamo ottenuto tutti punti che stanno sulla retta y = 2x. Abbiamo supposto che 2x sia proprio il valore esatto della pendenza di y = x² in corrispondenza della ascissa x.

2. Dimostrazione della congettura

Innanzi tutto testiamo questa congettura su un altro punto. Consideriamo il punto del grafico di ascissa 1, ossia il punto (1,1); (per x=1 x2=1).     La pendenza, in base alla formula ora trovata, dovrebbe essere 2; infatti per x = 1 2x = 2. La retta che passa per (1,1) e ha pendenza 2 è y = 2(x−1)+1. La disegno e vedo che effettivamente approssima bene l'andamento del grafico attorno ad x =1.     Proviamo a farlo anche attorno a 0.4.

[1]   Quanto è la pendenza in x = 0.4 in base alla formula trovata?  Spiegate come è stata disegnata la retta tratteggiata nella figura precedente?  Qual è l'ordinata del punto del grafico per cui essa passa?

La figura a lato ci aiuta a precisare meglio il significato della pendenza in un punto P in cui l'andamento non sia rettilineo: • si prende un archetto della curva che contenga P e si calcola la pendenza del segmento che ne congiunge gli estremi; • si ripete il calcolo prendendo un archetto più piccolo; • … e così via;  la pendenza in P è il valore su cui tende a stabilizzarsi questo procedimento.

In particolare abbiamo proceduto prendendo segmenti con estremi di ascissa equidistante da quella di P. Nella figura la distanza tra la ascissa degli estremi è stata chiamata h.
Proviamo a fare il calcolo per un generico punto P = (x, x²) del grafico di y = x².
Il punto A è (x-h, (x-h)²); il punto B è (x+h, (x+h)²); la pendenza del segmento AB è:

Δy / Δx  =  (y_B−y_A) / (x_B−A_A)  =  ((x+h)²)−(x−h)²)) / (2h)
=  ((x²+2xh+h²)−(x²−2xh+h²)) / (2h)  =  4xh / (2h)  =  2x

Per quanto piccolo prenda l'archetto, ossia comunque prenda h, ottengo sempre 2x. Questo dunque è il valore su cui il nostro procedimento inevitabilmente si stabilizza. Abbiamo così confermato la nostra congettura: la pendenza della curva y = x² in un punto di ascissa x è 2x.

3. La pendenza di y = x³

[3]   La figura a lato è un tratto della curva y = x3. Provate, con un ragionamento simile al precedente, a determinarne la pendenza in un generico punto P di ascissa x. Suggerimenti. • Potrebbe utile ricordare come si sviluppa un termine dalla forma (a+b)3 • A differenza del caso precedente, alla fine dovreste ottenere per Δy/Δx un termine in cui compare h. Cercate di capire che cosa tende a diventare questo termine man mano che si prende h di ordine di grandezza via via più piccolo (ossia per h che tende a 0).

Una volta che avete concordato una soluzione, sintetizzatela qua sotto.

Δ y  =    =       ...      →     ...        per h → 0 —— ————————————— Δ x 2h

[4]   Traccia il grafico di y = 3x² sullo stesso sistema di riferimento in cui è stato tracciato quello di y = x³. Osserva dove esso scende e dove sale. Sono proprio gli x per cui cresce/decresce la pendenza di y = x³? Quali sono questi x?

La pendenza diminuisce quando ...
La pendenza cresce quando ...

Nota. Noi abbiamo dedotto le formule per la pendenza di y = x2 e di y = x3 studiando come varia la pendenza media di archetti di curva con ascissa centrata in x. Gli stessi risultati li avremmo ottenuti prendendo gli archetti anche in altri modi, purché via via siano uno contenuto nel precedente e con ampiezza che tende a 0. Ad esempio nel caso dello studio della pendenza di una funzione che sia definita solo per x≥0, per trovare la pendenza in 0 dovremmo prendere degli archetti che hanno 0 come estremo sinistro, ossia calcolare pendenze del tipo raffigurato a fianco.

4. Come ricavare formule per la pendenza di nuove funzioni

Alla fine della scheda 2 vi è stato proposto un esercizio che dovrebbe avervi fatto capire che se dilato verticalmente un grafico viene moltiplicata per lo stesso fattore la sua pendenza. Un altro esempio: la curva y = 2.5x2 può essere ottenuta da y = x2 con una dilatazione verticale con fattore di scala 2.5 e, quindi, la pendenza è stata moltiplicata per 2.5;  la formula che esprime la pendenza in x di y = x2 è 2x, quindi quella che esprime la pendenza di y = 2.5x2 è 2·2.5x, ossia 5x. [5]   Qual è la pendenza del grafico di y = 4x3 nel punto di ascissa x?

Vediamo, ora, come ricavare la pendenza della somma di due funzioni, f e g, a partire dalle formule delle pendenze delle due singole funzioni.
A lato sono tracciati i grafici di y = f(x), y = g(x) e y = f(x)+g(x). Il grafico della "funzione somma" si ottiene da quello di f aggiungendo, punto per punto, all'ordinata quella del corrispondente punto del grafico di g.     Pensiamo al caso in cui f(x) e g(x) siano rispettivamente la popolazione maschile e quella femminile di un certo stato all'istante x. Se dall'istante x1 all'istante x2 la popolazione maschile varia di ΔM e quella femminile di ΔF, la variazione ΔT del totale della popolazione è la somma delle due variazioni (13 maschi in più e 11 femmine in più fanno 13+11 abitanti in più).     In generale, se indichiamo con Δh(x) la variazione da h(x1) a h(x2), possiamo scrivere: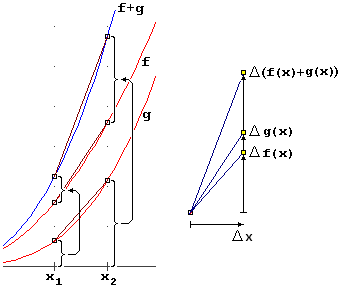
Δ(f(x) + g(x)) = Δf(x) + Δg(x) [la funzione somma ha come variazione la somma delle variazioni delle due funzioni sommate]

Quindi, nota la formula per le pendenze di f e di g, con una semplice somma possiamo ricavare quella della funzione somma.

Riprendiamo un problema della scheda 2:
devo realizzare una scatola tagliando da una lamiera quadrata di lato 20 [cm] quattro quadratini di lato x e operando successive piegature e saldature; come devo effettuare il taglio per ottenere il volume massimo?

[6]   Utilizzando le proprietà messe a fuoco in questo paragrafo, trova la formula che esprime la pendenza del grafico di V nel punto di ascissa x. Usa opportunamente questa formula per risolvere il problema.
[Suggerimento. Sviluppa prima il prodotto (20–2x)²x]

La funzione che rappresenta la pendenza del grafico della funzione f viene chiamata la funzione derivata (o semplicemente la derivata) di f. Il nome indica il fatto che è una funzione che non viene descritta direttamente, ma viene "ricavata" dalla funzione f. Per essa si usano diverse notazioni. Vediamone una, nelle due forme che assume a seconda che si specifichi o no il nome della variabile di input:

D(f) è la funzione derivata di f

Dx(f(x)) è la derivata di f(x).

[7]   Completa:
D_x(x²) = ....     D_z(5z³) = ....     D_u(4k + u + 3u²) = ....     D(F+G) = ....

5. La derivata della funzione  x → x^h

Abbiamo trovato che:
D_x(x³) = 3·x²,  e che  D_x(x²) = 2x, ovvero che:
D_x(x²) = 2·x¹.  Sappiamo anche che  D_x(x) = 1 (la retta y = x ha pendenza 1), ovvero che:
D_x(x¹) = 1·x⁰.  Proviamo a generalizzare al caso di un generico esponente n intero diverso da 0:
D_x(xⁿ) = ?

[8]   Congetturate come completare la formula precedente e scrivete la vostra conclusione qua sotto:
              se n ≠ 0   D_x(xⁿ) = ....

Questa congettura si può effettivamente dimostrare con un procedimento del tutto analogo a quello che abbiamo impiegato per i casi n = 2 e n = 3.
    Vediamo che cosa accade per n = −1, ossia per la derivata di x⁻¹, cioè 1/x.

D_x(1/x) = D_x(x⁻¹) = −1 · x⁻¹⁻¹ = −1 · x⁻² = −1/x²

Ecco i grafici della funzione di partenza (a sinistra) e della sua derivata (a destra):

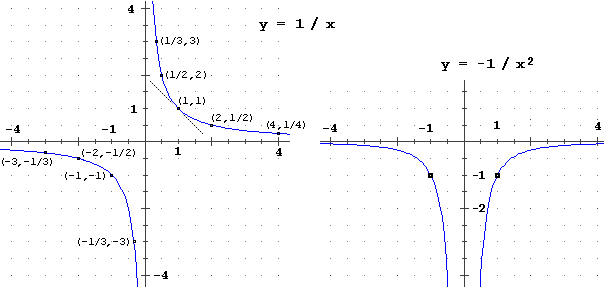
•  y = 1/x decresce sia per x < 0 che per x > 0, e in accordo con ciò la sua derivata è negativa (ha grafico che sta sotto all'asse y)
•  per x = 1 e per x = −1 y = 1/x ha tangente con pendenza −1, e la sua derivata per gli stessi x vale -1
•  man mano che x si allontana da 0, y = 1/x tende a diventare orizzontale, e la derivata −1/x² tende a valere 0 al crescere del valore assoluto di x.

[9]   D_x=c(f(x)) indica il valore della derivata di f in c. Ad es. la pendenza di A = L² nel punto di ascissa 3 è D_L=3(L²) = (2L)_L=3 = 6.  Osservando la figura seguente stabilite quanto vale:  D_A=9(√A) = ....

Un altro esempio. Quanto vale D_x=16(√x)?
Il grafico di y = √x è come il grafico di y = x² con gli assi scambiati; il punto di ascissa 16 corrisponde al punto di ascissa √16 = 4; la pendenza di y = x² in tal punto è D_x=4(x²) = 2·4; la pendenza di y = √x nel corrispondente punto è il reciproco (in quanto variazione orizzontale e verticale vengono scambiate): 1/(2·4) = 1/8.
    In generale:  D_x(√x) = 1/(2√x).

[10]   Spiega perché la formula ora vista può essere scritta nella forma:   D_x(x^1/2) = 1/2 · x^−1/2

Questa formula non è altro che un caso particolare della formula:

D_x(x^h) = h · x^{h − 1}

per h = 1/2. Infatti h − 1 = 1/2 − 1 = −1/2. Si può dimostrare che tale formula vale per ogni h ≠ 0, anche non intero.

[11]   Completa:     D_x( ³√x) = D_x(x^1/3) = ...

[12]   Sapendo che nel recipiente fatto a cono con vertice in basso considerato nella scheda 2 l'altezza in cm del liquido al passare del tempo in secondi è esprimibile con la formula seguente, stabilisci qual è la velocità v con cui sale il liquido a 100 secondi dall'inizio.

h(t) = 3 3√  10 t —— π	Dt(h(t)) = ...	v =   ...   cm/s
[suggerimento: usa le trasformazioni  3√(kx) →  3√k 3√x   e  Dx(k·f(x)) → k·Dx(f(x))]

[13]   Usando opportunamente il concetto di derivata, trova il vertice della parabola di equazione  y = 0.7 x² − x/3 + 2   [spiega come hai proceduto]