| Cognome Nome | ________________________________ | classe | __________________ |
La matematica dei cambiamenti - Scheda 4
1. Riepilogo
La tabella seguente riassume le proprietà studiate nella scheda 3:
| Dx(xh) = hxh−1 |
Dx(f(x)+g(x)) = Dx(f(x)) + Dx(g(x)) |
Dx(k · f(x)) = k · Dx(f(x)) |
| Esempi d'uso: |
Dx(x3) = 3x2
Dx(√x) = Dx(x1/2) = 1/(2√x)
Dt(1/t) = Dt(t−1) = −1/t2 |
Dx(x3+√x) = 3x2 + 1/(2√x)
Richiamiamo qualche applicazione. |
Dz(−5z3) = −5·3z2 = −15z2 |
| • Se P(t) rappresenta la posizione lungo una strada all'istante t,
Dt(P(t)), ossia la pendenza del grafico di P in funzione di t, rappresenta la velocità
all'istante t. |
Abbiamo visto che, nel caso di un recipiente in cui il livello h (cm) del liquido immesso
all'istante t (s) è dato dalla formula h = 3 3√(10t / π),
la velocità di innalzamento del liquido dopo 100 secondi è:
Dt=100(3(10t/π)1/3) = 3(10/π)1/3 Dt=100(t1/3)
= 3(10/π)1/3 (1/3·t−2/3)t=100
= 3(10/π)1/3 ·1/3·100−2/3
= (10/π)1/3 /100001/3 = 1/ 3√(1000π)
= 1/(10 3√π) = [con la calcolatrice] 0.068278..., ossia, arrotondando,
0.068 cm/s.
Ossia, se il liquido continuasse a innalzarsi
con la stessa velocità che ha all'istante t = 100 (s), dopo altri 100 s si innalzerebbe di 6.8 cm (vedi figura, in cui la pendenza
della retta "tangente" al grafico in t = 100 rappresenta la velocità in tale istante). |  |
• Abbiamo
visto che una scatola ottenuta tagliando da una lamiera quadrata di lato 20 [cm]
quattro quadratini di lato x ha volume V = (20–2x)2x.
Quando il volume è massimo quando (vedi figura) il grafico di V in funzione di x
ha pendenza nulla, ossia:
Dx((20–2x)2x) = 0
Dx(4x3−80x2+400x) = 0
12x2−160x+400 = 0
3x2−40x+100 = 0
x = 40/6 ± √(1600−1200)/6 = 20/3 ± 10/3
x = 10 oppure x = 10/3
Il volume è minimo (V=0) per x = 10 ed è massimo per x = 3.333... (cm).
|  |
• Il vertice della parabola di equazione
y = 0.7 x2 − x/3 + 2 corrisponde alla x in cui la derivata
è nulla:
Dx(0.7 x2 − x/3 + 2) = 0
1.4 x − 1/3 = 0
x = 1/3/1.4 = 5/21 = 0.23809...
L'ordinata è 0.7 (5/21)2 − 5/21/3 + 2 = 247/126 = 1.96031...
|  |
Studiamo, ora, la velocità con cui variano altri fenomeni.
2. Le catene di Sant'Antonio (chain letters)
[1] Questa lettera, del 1935, fa parte di una delle prime catene di Sant'Antonio (chain
letters - lettere a catena - in inglese). Cercate di capire come funziona la catena e spiegate come mai viene prospettato proprio quel ricavo (e in quali ipotesi lo si ottiene).
|
Mrs. Christine Galuppe | 828 29th St. | Denver, Colo.
|
| Miss Alice Ferguson | 1440 Marion St. | " " |
| Mrs. Carl Ferguson | 1440 Marion St. | " " |
| Miss Katharyn Wiley | 2317 Dexter St. | " " |
| Miss Thelma Hardy | 2317 Dexter St. | " " |
| Mrs. Villa Pickens | 1320 St. Paul St. | " " |
– This chain was started in the hope of bringing prosperity to you.
– Within three days make five copies of this letter, leaving off the name and address at the top and adding your name and address at the bottom, and mail to five friends to whom you wish prosperity to come.
– In omitting the top name, send that person ten cents (10c) wrapped in paper as a charity donation. In turn, as your name leaves the list you will receive 15 625 letters with donations amounting to $1 562.50.
– Now is this worth a dime to you?
– Have the faith your friend had and the chain will not be broken |
Nota. Le catene di Sant'Antonio sono nate più o meno quando si sono diffusi
il moderno sistema postale e la capacità di leggere e scrivere, tra fine '800 e inizio '900. Le prime avevano forma di gioco: erano lettere della "buona fortuna" inviate a persone che a loro volta dovevano ciascuna inviarne
copia a un dato numero di altre persone, con la promessa di una sorte favorevole
per chi prosegue la catena e la minaccia di disgrazie per chi la interrompe. Successivamente,
dopo la prima guerra mondiale, sono nate catene che prevedono l'invio
di denaro, come quella dell'esercizio, e, poi, anche vere e proprie truffe: alla gente viene chiesto di investire risparmi nell'avvio di qualche attività economica o di diventare
distributori di un certo prodotto e procacciare altri distributori. Con l'avvento
della posta elettronica il fenomeno si è esteso, a livello sia di scherzo
dannoso (messaggi che intasano le caselle di posta, che diffondono virus, …),
sia di truffa (ora le leggi vietano sia le "catene di sant'Antonio"
che possono creare danni, sia quelle attraverso cui vengono coinvolte le persone in imprese di tipo economico).
[2]
Non sappiamo se tutti proseguono la catena né quanti giorni impiegano a spedire le lettere e quanti queste ne impiegano ad arrivare. Supponiamo, per semplicità, che tutto
si svolga in modo uniforme e che passi esattamente una settimana tra l'arrivo della lettera
a una persona e l'arrivo di quelle che essa spedisce. Supponiamo, inoltre, che
ad ogni invio vengano contattate persone che non erano già state coinvolte
nella catena. Indichiamo con n il tempo
misurato in settimane da quando è stata inviata la prima lettera della catena e con
P(n) il numero persone a cui arriva la lettera
dopo n settimane.
Quanto vale P(0)? ____
Quanto vale P(1)? ____
Quanto vale P(2)? ____
Quanto vale P(5)? ____
Il grafico a lato rappresenta P(n) in funzione
di n.
Scegliete opportunamente la scala sull'asse verticale.
Esprimete P in funzione
di n mediante una formula.
P(n) = …
|
 |
Il numero delle persone coinvolte cresce vertiginosamente. La cosa
si vede anche sul grafico: la sua pendenza aumenta molto rapidamente,
tanto che, per riuscire a visualizzare P(5),
abbiamo dovuto scegliere una scala che ci fa apparire piatti i primi tratti del
grafico.
[3]
Proviamo ad esplicitare la pendenza dei vari tratti del grafico. In tutti i tratti n varia di 1 (passa da 0 a 1, poi da 1 a 2, ...): Δn = 1.
|
da 0 a 1: | P(0) = 1 | P(1) = 5 | ΔP = 5-1 = 4 | ΔP / Δn = 4/1 = 4 |
|
da 1 a 2: | P(1) = 5 | P(2) = 52 | ΔP = 52-5 = 5(5-1) = 4·5 | ΔP / Δn = 4·5 |
|
da 2 a 3: | P(2) = .... | P(3) = .... | ΔP = .... | ΔP / Δn = .... |
|
da n a n+1: | P(n) = .... | P(n+1) = .... | ΔP = .... | ΔP / Δn = .... |
3. La crescita esponenziale
Nel caso della catena di Sant'Antonio abbiamo visto che ogni settimana
il numero delle persone a cui viene spedita la lettera è 5 volte quello delle
persone contattate la settimana precedente:
P(n+1) = P(n)·5. L'incremento ΔP(n),
ossia P(n+1)-P(n), è pari a P(n)·5-P(n)
= P(n)·4: P(n) cresce con velocità proporzionale a P(n) stesso. Graficamente, abbiamo che la pendenza ΔP(n)/Δn dei vari tratti rettilinei cresce proporzionalmente alle ordinate.
Una crescita di questo tipo viene chiamata esponenziale in quanto il valore P(n) della grandezza può essere espresso come 5n, ossia mediante il calcolo di una potenza che ha l'input n come esponente. Studiamo un altro fenomeno di crescita esponenziale.
Vi sono vari tipi di microrganismi unicellulari che si riproducono per scissione: quando la cellula raggiunge una
certa dimensione si scinde in due. In particolari condizioni ambientali all'interno di una popolazione di una
di queste specie di microrganismi il tempo medio di vita di una cellula (ossia il tempo medio che passa
dalla scissione di una cellula a quello di una cellula da essa generata) è pressocché costante.
In alcuni microrganismi esso può essere di pochi minuti, in altri può essere di qualche giorno.
In queste condizioni esiste un intervallo di tempo T (tempo di duplicazione) tale che,
passando da un qualunque istante t all'istante t+T, la popolazione raddoppi:
infatti gli organismi non si scindono tutti esattamente nello stesso tempo,
cosicché nel complesso di una popolazione di svariati milioni di individui si ha un ininterrotto
duplicarsi di cellule che dà luogo a una crescita della popolazione praticamente continua e regolare, con velocità
di variazione proporzionale alla popolazione stessa.
Se iniziamo a misurare la popolazione a partire da un certo istante t = 0 e indichiamo con P(t) il numero per cui si è moltiplicata
dopo il tempo t,
ossia se P(t) è la popolazione misurata prendendo come unità la popolazione iniziale,
possiamo descrivere la situazione così:
P(0) = 1, P(t+T) = P(t)·2
ovvero P(t) = 2n se n è il numero delle duplicazioni avvenute nel tempo t.
Tenendo conto che n lo si ottiene dividendo t per il tempo di duplicazione T, abbiamo anche:
P(t) = 2 t / T.
Se da un rilevamento sperimentale ogni 5 minuti otteniamo i valori di P rappresentati graficamente sotto a sinistra, possiamo cercare di approssimare tali punti con una curva, come è fatto sotto a destra.
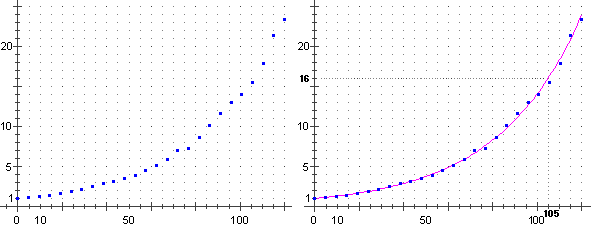
Ricaviamo che la popolazione si moltiplica per 16 in 105 minuti; 16 = 24; quindi 4T = 105 minuti.
Questi microrganismi duplicano la loro popolazione in 105/4 = 26.25 minuti, ossia in 26'15".
L'andamento di P in questo caso è dunque descrivibile con P(t) =
2 t / 26.25.
Poiché, con una calcolatrice, ho che 21/26.25 = 1.0268, posso descrivere il fenomeno anche con la formula:
P(t) = 1.0268 t.
[4] Per ottenere la formula precedente
si è usata la proprietà: a b · c = (ab )c. Che cosa si sono presi come a, b e c?
a = ....
b = ....
c = ....
Anche questa è una crescita esponenziale. In questo caso l'esponente non varia solo tra
i numeri naturali, come nel caso della catena di Sant'Antonio (in cui valutavamo il tempo di settimana in settimana), ma sui numeri reali (possiamo considerare quanti sono i microrganismi in un
qualunque istante t).
Anche in questo caso la velocità con cui varia P(t) è proporzionale a
P(t), come vedremo meglio nel prossimo paragrafo.
[5] Sappiamo che am/n, se m/n è una frazione non semplificabile, è definito come n√(am).
Esprimi sotto forma di composizione di un elevamento a un esponente intero e di una estrazione di radice
i seguenti numeri: 23.1, 23.14, 23.141 [traccia: 3.1 = 31/10, ...].
23.1 = ....
23.14 = ....
23.141 = ....
Secondo voi, che cos'è, ovvero come si calcola 2π?
4. La derivata delle funzioni esponenziali
Le funzioni del tipo y = ax (con a ≠ 1, se no
avremmo la funzione costante y = 1) sono dette esponenziali.
Abbiamo visto che se x varia sui numeri naturali queste funzioni variano con velocità
proporzionale al loro valore. Vediamo che la cosa vale anche sui numeri reali.
| Approssimo
Dx(ax), ossia la pendenza in x
del grafico di y = ax,
con quella del segmento che ne congiunge i punti di ascissa x−h e x+h:
|
 |
|
|
| Raccogliendo ax ho visto che la pendenza in un generico punto x
è pari al prodotto tra ax e
(a0+h-a0-h)/(2h), ossia
tra ax e la pendenza in 0, ossia: |
|
Dx(ax) = k · ax
con k = Dx=0(ax)
|
Considero ad es. y = 2x.
Calcolo la sua pendenza per x=0 nel modo seguente:
|
 |
| h = 1 |
(2h−2−h) / (2h) =
(21−2−1) / 2 | = 0.75 |
| h = 0.1 |
(2h−2−h) / (2h) =
(20.1−2−0.1) / 0.2 | = 0.6937023... |
| h = 0.01 |
(2h−2−h) / (2h) =
(20.01−2−0.01) / 0.02 | = 0.6931527... |
| h = 0.001 |
(2h−2−h) / (2h) =
(20.001−2−0.001) / 0.002 | = 0.6931472... |
Vedo che mi stabilizzo su un valore arrotondabile a 0.693.
Dunque Dx=0(2x) = 0.693 (valore arrotondato) e Dx(2x) = k·2x con k = 0.693.
Il grafico della pendenza di y = 2x è dunque come quello di y = 2x ma schiacciato, ovvero con le ordinate tutte moltiplicate per k.
[6] Valuta quanto vale la derivata di 3x per x=0 procedendo come sopra e schizza i grafici di y = 3x e della sua pendenza:


5. Il numero e
Per calcolare la derivata di una funzione esponenziale basta conoscere la sua derivata in 0. Si intuisce come possa essere comodo disporre una funzione esponenziale che in 0 abbia derivata 1.
Le curve y = 2x e y = 3x per x = 0 hanno una pendenza minore di 1, l'altra maggiore di 1. Affinché y = ax abbia pendenza 1 occorre che la base, ossia a, sia compresa tra 2 e 3. Attraverso una ricerca per tentativi, provando con 2.1, 2.2, 2.3, ... si trova che deve essere compreso tra 2.6 e 2.7 in quanto y = 2.6x e y = 2.7x hanno in 0 una pendenza minore, l'altra maggiore di 1. Procedendo così si possono trovare tutte le cifre che si vogliono di un tale numero a.

Il numero a che ha questa proprietà viene convenzionalmente indicato con e: y = ex ha in 0 pendenza 1, e, quindi, il grafico della
sua pendenza coincide con il suo stesso grafico. In altre parole:
Dx(e x ) = e x
Si può calcolare che e = 2.71828182845…. È
un numero non razionale (irrazionale), ossia che non può essere calcolato eseguendo la
divisione tra due particolari numeri interi; esistono comunque molti procedimenti per generarne facilmente le cifre; le calcolatrici
scientifiche ne hanno tutte incorporato uno. Vediamo come possiamo, ora, calcolare le derivate della altre funzioni esponenziali.
y = 2x
ha il grafico di y = ex dilatato orizzontalmente: passa anch'esso per
(0,1) ma ha pendenza k = Dx=0(2x) = 0.693... invece che 1.
Per passare da un grafico all'altro basta che moltiplichi o divida le ascisse per k. Questa osservazione
ci consente (vedi figura) di dire che k è il numero tale che ek = 2.
Analogamente dal grafico di y = 3x si passa a quello di y = ex moltiplicando le ascisse per la pendenza del primo in 0, ossia
per k = Dx=0(3x). In particolare (1,3) diventa (k,3), ossia
k è l'ascissa del punto di ordinata 3 del grafico di ex: k è il numero tale che ek = 3.
|  |
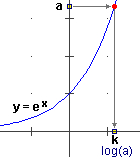 |
In generale la pendenza di y = ax, ossia
Dx=0(ax), è il numero k
tale che ek = a.
Tale numero è indicato con log(a) ed è calcolabile con un
apposito tasto di funzione, [log], presente su tutte le calcolatrici scientifiche.
log indica la funzione inversa della funzione esponenziale di base e (vedi figura a lato) e viene chiamata funzione logaritmo.
Concludendo:
Dx(ax) = k · ax
con k = Dx=0(ax) = log(a)
|
Con una calcolatrice possiamo ritrovare: log(2) = 0.693147180559945...,
log(3) = 1.0986122886681...
[7] Come sarà fatto il grafico della funzione logaritmo?
Prova a schizzarlo qua sotto.












