Cognome Nome

________________________________

classe

__________________

La matematica dei cambiamenti - Scheda 6

1. Ordine di grandezza dei numeri

Le scritture 8.3628·10⁴, 2.49·10 ^-2 e in generale le scritture h·10ⁿ in cui h è un numero compreso tra 1 e 10 (1 ≤ h < 10) vengono dette in notazione scientifica; è la notazione impiegata dalle calcolatrici per rappresentare i risultati che non stanno per esteso sul visore.
    È comoda anche per rappresentare in modo comprensibile le approssimazioni. Ad esempio se volessi arrotondare il numero 319 624 a tre cifre significative dovrei scrivere 320 000 in quanto la quarta cifra (6) è maggiore di 4 (3196 è più vicino a 3200 che a 3190); ma di fronte a 320 000 come farei a capire che le cifre significative sono tre e non solo due?  Usando la notazione scientifica, 3.20·10⁵, scioglierei ogni dubbio; se le cifre significative fossero state solo due avrei scritto 3.2·10⁵.

    Il concetto di ordine di grandezza non solo facilita la descrizione sia dei valori molto grandi (milioni, miliardi, …) che di quelli molto piccoli (milionesimi, miliardesimi), ma anche la loro rappresentazione grafica quando compaiono assieme sia gli uni che gli altri. Consideriamo un esempio.

[1]   La figura a lato rappresenta graficamente come le specie si distribuiscono per classi dimensionali, mettendo in luce come vi siano poche specie di animali "grandi" e molte di animali "piccoli": le specie animali con dimensioni tra 5 e 10 metri sono 6, quelle con dimensioni tra 5 mm e 1 cm sono 520 mila.     Le frequenze assolute sono state rappresentate sull'asse verticale usando una scala particolare: la distanza tra una divisione e l'altra rappresenta potenze di 10 man mano crescenti: alla divisione "0", più in basso è stato associato il valore 100 = 1, alla divisione "1" è stato associato il valore 101 = 10, alla "2" il valore 102 = 100, …     Ad es. le specie con dimensioni tra 5 e 10 cm sono circa 10 mila, ossia 104, e il valore è stato associato alla divisione "4". Le specie di dimensioni più grandi sono 6, compreso tra 100 e 101, e a 6 è stata associata una posizione intermedia tra 0 e 1, precisamente corripondente all'esponente da dare a 10 per ottenere 6. Verifica (come?) che questo numero è compreso tra 0.778 e 0.779.

2. Le funzioni logaritmo

Nell'es. precedente i valori delle frequenze assolute sono stati segnati in corrispondenza dei loro ordini di grandezza; ad es. 10 mila corrisponde alla tacca 4 in quanto 10⁴=10000; 6 è stato segnato in corrispondenza di 0.778… in quanto 10^0.778…=6.

    Nel fare ciò abbiamo esteso il concetto di ordine di grandezza passando dalle potenze ad esponente intero a quelle ad esponente reale. Mentre per 10000 possiamo dire che il suo ordine di grandezza è 4, per 6 diciamo che 0.778… è il suo logaritmo decimale; simbolicamente si scrive: 0.778… = Log(6).
    In modo sintetico possiamo dire che la funzione Log è la funzione inversa di x → 10^x:
h è il logaritmo decimale di k se 10^h = k.

    La scala verticale usata nel diagramma precedente viene chiamata scala logaritmica in quanto i valori sono rappresentati a distanze proporzionali non ai valori stessi ma ai loro logaritmi decimali. Si tratta di una scala che si usa quando si vogliono rappresentare assieme valori con ordini di grandezza molto diversi: in una usuale scala come avremmo potuto rappresentare assieme 6, 900, 10000 e 520000? non saremmo stati in grado di differenziare i primi tre valori, che si sarebbero ammucchiati in uno stesso punto dell'asse.

    In questa e nelle precedenti schede abbiamo introdotto due esempi di funzioni logaritmiche, ossia di funzioni inverse di funzioni esponenziali:
• la funzione log, inversa di x → e^x, detta logaritmo naturale e indicata anche col simbolo ln,
• la funzione Log, inversa di x → 10^x, detta logaritmo decimale.
    Più in generale per ogni numero positivo a diverso da 1, si chiama logaritmo in base a e si indica log_a  la funzione inversa di x → a^x. In particolare abbiamo che  Log = log₁₀ e che  log = log_e.

[2]   Risolvi rispetto a x le equazioni:   (a)  log₃(x) = 2   e   (b)  log₃(3^2x) = 8

    Ecco i grafici di due funzioni logaritmiche, una con base maggiore di 1, l'altra con base minore di 1, con tratteggiati i grafici delle funzioni esponenziali di cui sono le inverse:

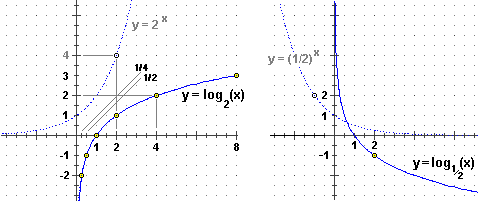
Il grafico soprastante a sinistra è, in particolare, quello del logaritmo binario, ossia in base 2

    Dalle proprietà delle potenze discendono particolari proprietà dei logaritmi. In particolare:
• dal fatto che a^b+c = a^b·a^c, ossia che x → a^x trasforma la somma di due input nel prodotto degli output, segue che la funzione inversa trasforma, inversamente, il prodotto degli input nella somma degli output:

log_a(p · q) = log_a(p) + log_a(q)

Ad esempio il ragionamento con cui si trasforma 1000·100 è in 10²⁺³ può essere interpretato così:  "a che cosa devo elevare 10 per ottenere 1000·100? alla somma degli esponenti a cui lo elevo per ottenere 1000 e 100", ossia:  Log(1000·100) = Log(1000)+Log(100).
• dal fatto che a^-b = 1/a^b, ossia che x → a^x trasforma l'opposto di un input nel reciproco dell'output, segue che la funzione inversa trasforma, inversamente, il reciproco di un input nell'opposto dell'output:

log_a(1/q) = – log_a(q)

Ad esempio:  "a che cosa devo elevare 10 per ottenere 1/1000? all'opposto del numero a cui lo elevo per ottenere 1000", ossia:  Log(1/1000) = –Log(1000) = –3.
• dal fatto che a^b–c = a^b/a^c, ossia che x → a^x trasforma la differenza di due input nel rapporto degli output, segue che la funzione inversa trasforma, inversamente, il rapporto degli input nella differenza degli output:

log_a(p / q) = log_a(p) – log_a(q)

• Che cosa possiamo dire di  log_a(p³)?
Usando la prima formula riportata in questo punto abbiamo:  log_a(p³) = log_a(p·p·p) = log_a(p) + log_a(p)+log_a(p) = 3 · log_a(p).  In generale si ha:

log_a(p^q) = q · log_a(p)

anche se q non è intero; questa formula corrisponde alla proprietà delle potenze  a^b·c = (a^b)^c.

[3]   Le proprietà precedenti sono facili da ricordare se si pensa al logaritmo in base dieci, e alla sua interpretazione come ordine di grandezza (o.d.g.). Completa la seguente tabella:

loga(p · q) = loga(p) + loga(q)	l'o.d.g di   10m · 10n   è   m+n
loga(1/q) = – loga(q)	l'o.d.g di   1/10n   è    …
loga(p / q) = loga(p) – loga(q)	l'o.d.g di   10m / 10n   è    …
loga(pq) = q · loga(p)	l'o.d.g di   (10m )n   è    …

Da come è la derivata delle funzioni esponenziali possiamo ricavare come è quella delle loro funzioni inverse. In particolare:

D(log)(x) = 1/x Infatti D(log)(x) è la pendenza della tangente r al grafico della funzione log nel punto di ascissa x; nella figura a lato abbiamo indicato con y l'ordinata log(x) di tale punto. Il grafico della funzione inversa (x → ex) ha ascisse e ordinate scambiate; la pendenza da noi cercata è quindi il reciproco di quella della tangente s a questo grafico nel punto (y,x). s ha pendenza pari alla derivata di x → ex in y; la derivata di questa funzione coincide con la funzione stessa, quindi la pendenza di s è ey. Ma ey = x, e 1/x è dunque la pendenza di r . In breve:   Dx(log(x)) = 1 / Dy(ey) = 1/ey = 1/x.

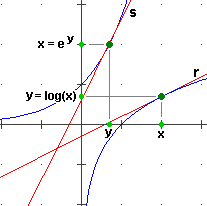    Il logaritmo naturale è quello che ha la derivata con l'espressione più semplice. Le derivate delle altre funzioni logaritmiche possono essere ricondotte a questa. Un modo semplice per farlo è ricorrere a un trucco che (come vedrai nel corso degli studi) risulta essere comodo in molte occasioni: usare opportunamente le trasformazioni  x = e^log(x)  e  log(p^q) = q·log(p).
    Vediamo, dunque, come esprime un logaritmo in una base generica mediante i logaritmi naturali:

log_a(x) = log_a(e^log(x)) = log(x)·log_a(e)

per esprimere log_a(e) usando solo log basta pensare al significato del logaritmo:
k = log_a(e) significa che a^k = e, ossia, elevando a 1/k, che a = e^1/k, ossia che log(a) = 1/k, ossia che log_a(e) = k = 1/log(a). Quindi:

log_a(x) = log(x) / log(a)

In definitiva, usando la proprietà D_x(k·f(x)) = k·D_x(f(x)):

D_x(log_a(x)) = D_x(log(x)/log(a)) = D_x(log(x)) / log(a) = 1/(x·log(a))

Riassumendo, le derivate della funzione esponenziale e della funzione logaritmo di base a si ottengono da quelle di x → e^x e di x → log(x), rispettivamente, moltiplicando e dividendo per log(a). Per ricordarsi "velocemente" che si deve moltiplicare nel caso dell'esponenziale (e, quindi, dividere in quello del logaritmo) si pensi che, se a > e, y = a^x ha pendenza maggiore di y = e^x e che, quindi, si deve trattare di una moltiplicazione per log(a), essendo log(a) > 1.

[4]   Sia G(t) una grandezza che decresce esponenzialmente al trascorre del tempo t secondo la formula G(t) = K·a^t, dove K è il valore iniziale della grandezza. Esprimi con una formula in cui compare log il tempo di dimezzamento di G  (traccia: devi cercare T tale che G(0+T) = G(0)/2, ossia tale che …; applica la funzione log ad entrambi i membri di questa formula e usa le sue proprietà).