Progetto Lauree Scientifiche - La Spezia - Stage
Avete visto che la matematica può facilitare lo studio di come variano
certi fenomeni, ad esempio la crescita di una popolazione
di animali in opportune condizioni,
il cambiamento della temperatura di un corpo dopo che viene spostato in un ambiente più
caldo o più freddo, la posizione di un corpo sottoposto all'azione di alcune forze, ...
Oggi svolgeremo alcune nuove attività legate a questa problematica. Le affronterete
voi da soli, suddivisi in gruppi composti da alunni di classi diverse. Qui vi vengono presentati i problemi,
tutti assieme; alcuni hanno un'impostazione simile ad alcuni problemi "scolastici", altri saranno invece
per voi forse un po' insoliti. Sta ad ogni gruppo organizzarsi per risolverli, nell'ordine che preferisce, lavorando su un problema per volta
o su più problemi assieme.
Quando un gruppo pensa di aver risolto un problema, viene a presentarci la sua soluzione. Noi gli diremo
se è giusta o sbagliata; nel secondo caso potrà tentare di trovare una nuova soluzione. "Vincerà" il gruppo che, entro due ore, affronterà in maniera soddisfacente
il maggior numero di problemi (a parità di numero di problemi risolti, si sceglierà il gruppo
che ha dato le soluzioni migliori).
ATTIVITÀ 1



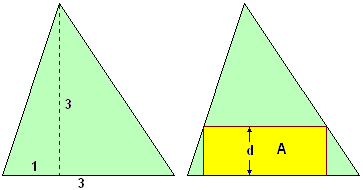
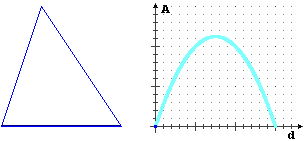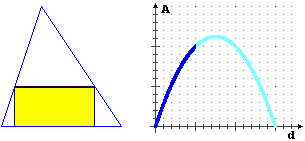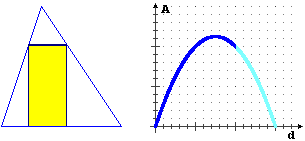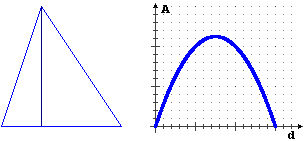
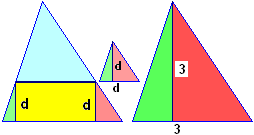
Considerate il triangolo raffigurato in alto (le dimensioni sono in metri). Il grafico successivo illustra come cambia l'area A di un rettangolo piazzato nel modo raffigurato (un lato collocato sul lato lungo 3 del triangolo, due vertici collocati sugli altri lati) al variare della distanza d. Quanto deve valere d affinché il rettangolo abbia area massima. Motivate la risposta.
I "moduli" che si aprono cliccando (se hai il browser impostato "a schede",
clicca col pulsante destro del mouse e seleziona "apri in una nuova finestra", non "in una nuova scheda") contengono dei modelli matematici che simulano lo sviluppo di una
particolare popolazione di animali, il primo nel caso essa viva in una ambiente dalle risorse illimitate,
il secondo in quello in cui viva in un ambiente chiuso (potrebbe essere una valle circondata da montagne).
Cercate di descrivere a parole come varia l'andamento di questa seconda popolazione di animali in funzione del tempo
(suggerimento: tracciate il grafico della popolazione in funzione del tempo).
Modelli "ideali" di questo tipo, in cui l'evoluzione di una popolazione è rappresentata
mediante un procedimento di calcolo (simile a quello "incorporato"
nei nostri moduli) che consente di calcolare la popolazione
ATTIVITÀ 3
CLICCA
Il modulo che si apre cliccando contiene una versione del Game of Life. Si tratta di
un particolare automa cellulare, ossia un
modello che simula la riproduzione di un insieme di cellule che evolvono in modo deterministico
a partire da una particolare
configurazione iniziale.
È stato ideato da Jhon Horton Conway nel 1970, ed ha dato il via
sia a molti video-giochi, sia alla messa a punto di modelli di simulazione per lo studio effettivo di vari fenomeni
reali.
Leggete l'help, provate ad usare il programma e poi trovate almeno
un esempio di configurazione stabile formata da 5 cellule e
un esempio di configurazione oscillante formata da 3 cellule.
ATTIVITÀ 4
CLICCA
Vi sono alcune foreste (ad es. in Canada e negli USA) in cui si verificano situazioni di questo tipo:
certi animali nocivi defogliano un dato tipo di pianta; quando queste piante muoiono vengono rimpiazzate da
un'altra specie, non gradita ai parassiti; una volta che i parassiti sono andati via gradatamente le
piante originali, capaci di sfruttare meglio le sostanze del terreno e la luce solare,
riprendono possesso del territorio; e il ciclo si ripete.
Il modulo che si apre cliccando contiene un modello che dà un'idea di questo fenomeno di infestazione. Mentre il "gioco-vita"
era a due stati (ogni zona poteva contenere una cellula [#] o essere vuota [ ]),
questo modello è a tre stati: ogni zona può essere verde [ ], infestata [#]
o defogliata [O]. Guardate gli esempi e provate ad usare il programma.
(1) Cercate di individuare le regole che governano l'evoluzione delle infestazioni,
ossia come cambia la configurazione ogni volta che premete [Passo].
(2) Nel caso dell'infestazione permanente dell'esempio 2, arrivati allo stadio raffigurato sotto:
1 2 3 4 5 6 7
01234567890123456789012345678901234567890123456789012345678901234567890123456789
0 : : : : : : :
1 : : : : : : :
2 : : : : : : :
3 : : : : : : :
4 : : : : : : :
5 : : : : : : :
6 : : : : : : :
7 : # # : : : : :
8 : #0#0# : : : : :
9 : #0:0 0# : : : : :
10-----------------#0--#--0#------------------------------------------------------
1 : #0:0 0# : : : : :
2 : #0#0# : : : : :
3 : # # : : : : :
4 : : : : : : :
5 : : : : : : :
si vede che se defoglio la zona infestata riga-10, colonna-21 la infestazione si allontana,
ossia non si autoriproduce più. Questa zona è il focolaio dell'infestazione, ossia è il territorio formato dal minor numero possibile di
zone infestate che, se defogliate in questo stadio, fanno sì che l'infestazione si allontani. Verificate
in questo caso se lo stesso effetto lo si può ottenere invece che defogliando il focolaio
defogliando le zone verdi ad esso ortogonalmente adiacenti (ossia facendo "terra bruciata" attorno ad esso).ATTIVITÀ 5
Negli esempi precedenti abbiamo studiato fenomeni che evolvono in modo "deterministico".
Gran parte dei fenomeni, invece, evolvono in maniera casuale. C'è un'area della matematica,
il calcolo delle probabilità, che si occupa dello studio dei fenomeni casuali e che
cerca di individuare dei metodi per interpretare o fare delle previsioni
relative all'andamento di questi fenomeni. Proviamo a fare qualcosa anche noi, su un esempio
molto semplice.
Consideriamo un fenomeno (rappresentabile numericamente) che assuma ripetutamente, e in modo del tutto casuale,
valori che cadono nell'intervallo [0, 1). Supponiamo che questi valori si distribuiscano uniformemente,
ossia che, presi comunque due sottointervalli di [0,1) di eguale ampiezza, le frequenze relative con cui
i valori cadono in essi tendono ad essere uguali. Ad esempio sia in [0,0.5) che in [0.5,1)
i valori tendono a cadere con la frequenza del 50% o, come si dice, hanno il 50% di probabilità
di cadere nell'uno e il 50% di probabilità di cadere nell'altro.
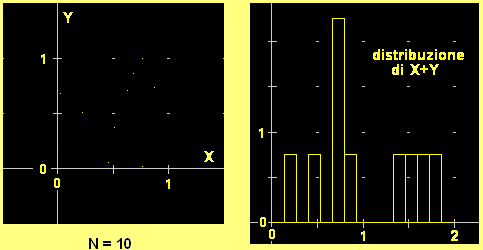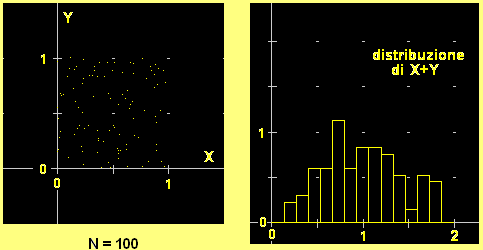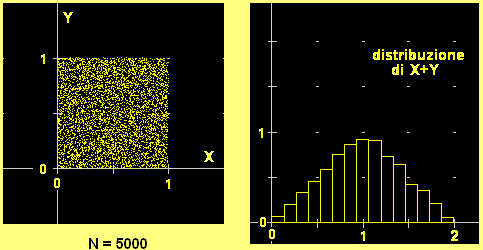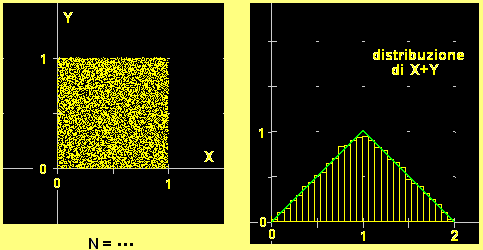
Generiamo, ripetutamente, due numeri casuali X e Y che si distribuiscono uniformemente in [0,1). La figura sopra a sinistra
illustra il fenomeno tracciando via via i punti che hanno X e Y come coordinate.
(1) Qual è la probabilità che il punto (X,Y) cada a distanza inferiore di 1 da (0,0)?
(2) La figura a destra illustra come si distribuiscono i valori di X+Y. Qual è la probabilità
che X+Y sia minore di 1/2?
(3) Provate a spiegare perché i valori di X+Y di distribuiscono nel modo illustrato a destra.